Maison >développement back-end >Tutoriel Python >Comment implémenter l'algorithme de recherche du premier chemin en largeur et en profondeur du graphique en Python
Comment implémenter l'algorithme de recherche du premier chemin en largeur et en profondeur du graphique en Python
- 王林avant
- 2023-06-02 23:42:011547parcourir
Préface
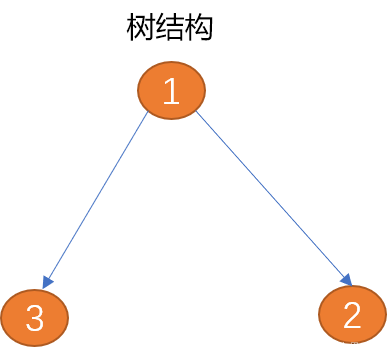
Le graphique est une structure de données abstraite, et son essence est la même que la structure arborescente.
Par rapport aux arbres, les graphiques sont fermés et la structure arborescente peut être considérée comme le prédécesseur de la structure graphique. Si vous appliquez des connexions horizontales entre des nœuds frères ou des nœuds enfants à une structure arborescente, vous pouvez créer une structure graphique.
Tree convient pour décrire une structure de données un-à-plusieurs de haut en bas, comme la structure organisationnelle d'une entreprise.
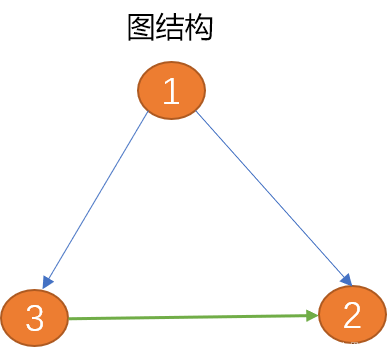
Les graphiques conviennent pour décrire des structures de données plusieurs-à-plusieurs plus complexes, telles que des relations sociales de groupe complexes.
1. Théorie des graphes
Utiliser des ordinateurs pour résoudre des problèmes le monde réel Lorsqu'on traite des problèmes, en plus de stocker des informations dans le monde réel, il est également nécessaire de décrire correctement la relation entre les informations.
Par exemple, lors du développement d'un programme de cartographie, il est nécessaire de simuler correctement la relation entre les villes ou les routes de la ville sur l'ordinateur. Ce n'est que sur cette base que des algorithmes peuvent être utilisés pour calculer le meilleur chemin d'une ville à une autre, ou d'un point de départ spécifié à un point de destination.
De même, il existe des cartes d'itinéraires de vol, des cartes d'itinéraires de train et des cartes de communication sociale.
La structure du graphique peut refléter efficacement les relations complexes entre les informations, comme mentionné ci-dessus, dans le monde réel. Cet algorithme peut être utilisé pour calculer facilement le chemin le plus court sur un itinéraire aérien, le meilleur plan de transfert sur un itinéraire ferroviaire, qui a la meilleure relation avec qui dans le cercle social et qui est le plus compatible avec qui dans le réseau matrimonial. ..
1.1 La notion de graphe
Vertex : Le sommet est aussi appelé nœud, et un graphe peut être considéré comme une collection de sommets. Les sommets eux-mêmes ont une signification en matière de données, ils porteront donc des informations supplémentaires, appelées « charge utile ».
Les sommets peuvent être des villes, des noms de lieux, des noms de stations, des personnes dans le monde réel... #Edge :
Les arêtes du graphique sont utilisées pour décrire la relation entre les sommets. Les arêtes peuvent avoir ou non une direction. Les arêtes directionnelles peuvent être divisées en arêtes unidirectionnelles et arêtes bidirectionnelles.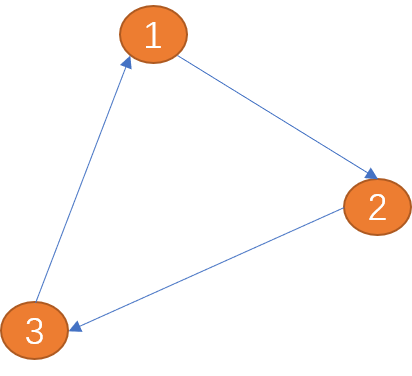
Comme indiqué ci-dessous, l'arête entre (point 1) et (sommet 2) n'a qu'une seule direction (la flèche indique la direction),
L'arête entre (sommet 1) et (sommet 2) a deux directions (flèches bidirectionnelles), est appelée arête bidirectionnelle.
La relation entre les villes est à double sens.
Poids : Des informations sur la valeur peuvent être ajoutées au bord, et la valeur ajoutée est appelée
weight. Les arêtes pondérées décrivent la force d’une connexion d’un sommet à un autre.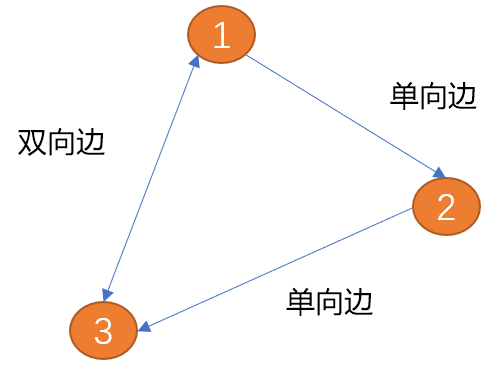 
Les bords décrivent les sommets La relation entre eux et le poids décrivent la différence de connexion.
Chemin :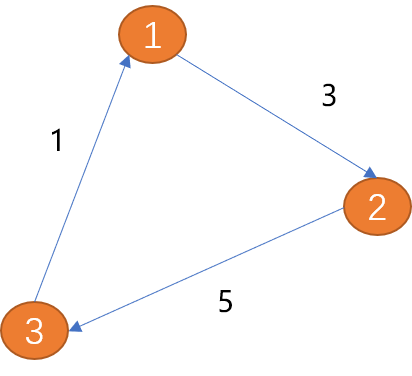
Premièrement comprendre le concept de chemin dans le monde réel# 🎜🎜#
Par exemple : lorsque vous conduisez d'une ville à une autre, vous devez d'abord déterminer l'itinéraire. Autrement dit, Par quelles villes devez-vous passer du point de départ à la destination ? Combien de kilomètres cela prendra-t-il ?
On peut dire qu'un chemin est une séquence composée de sommets reliés par des arêtes. Puisqu'il existe plusieurs chemins, la description du chemin d'un point d'élément à un autre point d'élément ne fait pas référence à un seul type.
Comment calculer des chemins dans des structures graphiques ?
La longueur d'un chemin non pondéré est le nombre d'arêtes sur le chemin.
La longueur d'un chemin pondéré est la somme des poids des bords sur le chemin.
Comme indiqué ci-dessus, la longueur du chemin du (sommet 1) au (sommet 3) est de 8.
- Boucle :
Partir du point de départ et enfin revenir au point de départ (le point final est aussi le point de départ) formera une boucle. chemin. Comme ci-dessus
est une bague.
Types de photos :
En résumé, les photos peuvent être divisées dans les catégories suivantes : (V1, V2, V3, V1)# 🎜 🎜#
Graphique orienté : Un graphe avec des arêtes directionnelles est appelé graphe orienté.
- Graphique non orienté :
- Un graphe sans direction d'arêtes est appelé un graphe non orienté.
- Un graphique avec des informations de poids sur les bords est appelé un graphique pondéré.
- Un graphe sans cycles est appelé graphe acyclique.
- Un graphe orienté sans cycle, appelé DAG.
1.2 Définition du graphe
- Selon les caractéristiques du graphe, la structure de données du graphe doit contenir au moins deux types d'informations : # 🎜🎜#
Tous les sommets forment un ensemble d'informations, représenté ici par V (par exemple, dans un programme cartographique, toutes les villes sont formées dans un ensemble de sommets).
Toutes les arêtes constituent un ensemble d'informations, représentées ici par E (description de la relation entre les villes).
Comment décrire les bords ?
Les bords sont utilisés pour représenter la relation entre les points des éléments. Ainsi, un bord peut inclure 3 métadonnées (point de départ, point final, poids). Bien entendu, les poids peuvent être omis, mais généralement lors de l’étude de graphiques, ils font référence à des graphiques pondérés.
Si
Gest utilisé pour représenter le graphique, alorsG = (V, E). Chaque arête peut être décrite par un tuple(fv, ev)ou un triplet(fv, ev, w).G表示图，则G = (V, E)。每一条边可以用二元组(fv, ev)也可以使用 三元组（fv,ev,w）描述。fv表示起点，ev表示终点。且fv，ev数据必须引用于V集合。
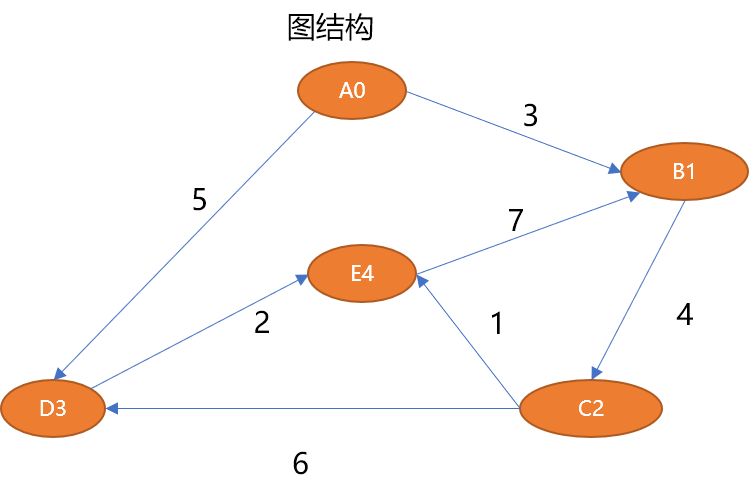
如上的图结构可以描述如下：
# 5 个顶点 V={A0,B1,C2,D3,E4} # 7 条边 E={ (A0,B1,3),(B1,C2,4),(C2,D3,6),(C2,E4,1),(D3,E4,2),(A0,D3,5),(E4,B1,7)}1.3 图的抽象数据结构
图的抽象数据描述中至少要有的方法：
Graph ( )： 用来创建一个新图。add_vertex( vert )：向图中添加一个新节点，参数应该是一个节点类型的对象。add_edge(fv，tv )：在 2 个项点之间建立起边关系。add_edge(fv，tv，w )：在 2 个项点之间建立起一条边并指定连接权重。find_vertex( key ): 根据关键字 key 在图中查找顶点。find_vertexs( )：查询所有顶点信息。find_path( fv,tv)：查找.从一个顶点到另一个顶点之间的路径。
2. 图的存储实现
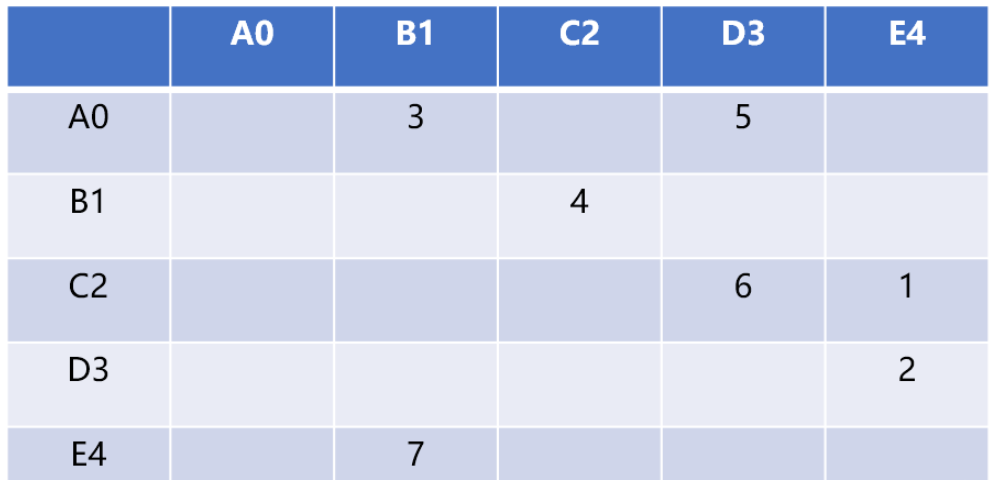
图的存储实现主流有 2 种：邻接矩阵和链接表，本文主要介绍邻接矩阵。
2.1 邻接矩阵
使用二维矩阵（数组）存储顶点之间的关系。
如
graph[5][5]可以存储 5 个顶点的关系数据，行号和列号表示顶点，第 v 行的第 w 列交叉的单元格中的值表示从顶点 v 到顶点 w 的边的权重，如grap[2][3]=6表示 C2 顶点和 D3 顶点的有连接（相邻），权重为 6
相邻矩阵的优点就是简单，可以清晰表示那些顶点是相连的。由于并非每对顶点之间都存在连接，因此矩阵中存在许多未被利用的空间，通常被称为“稀疏矩阵”。
只有当每一个顶点和其它顶点都有关系时，矩阵才会填满。如果图结构的关系不是太复杂，使用这种结构存储图数据会浪费大量的空间。
邻接矩阵适合表示关系复杂的图结构，如互联网上网页之间的链接、社交圈中人与人之间的社会关系……
2.2 编码实现邻接矩阵
因顶点本身有数据含义，需要先定义顶点类型。
顶点类：
""" 节（顶）点类 """ class Vertex: def __init__(self, name, v_id=0): # 顶点的编号 self.v_id = v_id # 顶点的名称 self.v_name = name # 是否被访问过:False 没有 True:有 self.visited = False # 自我显示 def __str__(self): return '[编号为 {0}，名称为 {1} ] 的顶点'.format(self.v_id, self.v_name)顶点类中
v_id和v_name很好理解。为什么要添加一个visited？这个变量用来记录顶点在路径搜索过程中是否已经被搜索过，避免重复搜索计算。
图类：图类的方法较多，这里逐方法介绍。
初始化方法
class Graph: """ nums:相邻矩阵的大小 """ def __init__(self, nums): # 一维列表，保存节点，最多只能有 nums 个节点 self.vert_list = [] # 二维列表，存储顶点及顶点间的关系(权重) # 初始权重为 0 ，表示节点与节点之间还没有建立起关系 self.matrix = [[0] * nums for _ in range(nums)] # 顶点个数 self.v_nums = 0 # 使用队列模拟队列或栈，用于广度、深度优先搜索算法 self.queue_stack = [] # 保存搜索到的路径 self.searchPath = [] # 暂省略……初始化方法用来初始化图中的数据类型：
一维列表
vert_list保存所有顶点数据。二维列表
matrix保存顶点与顶点之间的关系数据。queue_stack使用列表模拟队列或栈，用于后续的广度搜索和深度搜索。怎么使用列表模拟队列或栈？
列表有
append()、pop()2 个很价值的方法。append()用来向列表中添加数据，且每次都是从列表最后面添加。pop()默认从列表最后面删除且弹出数据，pop(参数)可以提供索引值用来从指定位置删除且弹出数据。使用 append() 和 pop() 方法就能模拟栈，从同一个地方进出数据。
使用 append() 和 pop(0) 方法就能模拟队列，从后面添加数据，从最前面获取数据
searchPathfvreprésente le point de départ etevreprésente le point final. Et les donnéesfv,evdoivent être référencées dans la collectionV.
La structure du graphe ci-dessus peut être décrite comme suit : 🎜 """ 添加新顶点 """ def add_vertex(self, vert): if vert in self.vert_list: # 已经存在 return if self.v_nums >= len(self.matrix): # 超过相邻矩阵所能存储的节点上限 return # 顶点的编号内部生成 vert.v_id = self.v_nums self.vert_list.append(vert) # 数量增一 self.v_nums += 11.3 Structure de données abstraite du graphe
🎜Au moins la méthode qui doit être incluse dans la description des données abstraites du graphe : 🎜- 🎜
Graph ( ): Utilisé pour créer un nouveau graphique. 🎜 - 🎜
add_vertex( vert ): Ajoutez un nouveau nœud au graphique, le paramètre doit être un objet de type nœud. 🎜 - 🎜
add_edge(fv, tv): Établissez une relation de bord entre 2 points d'élément. 🎜 - 🎜
add_edge(fv,tv,w): Établissez une arête entre 2 points d'élément et spécifiez le poids de connexion. 🎜 - 🎜
find_vertex( key ): Recherchez des sommets dans le graphique en fonction du mot-clé clé. 🎜 - 🎜
find_vertexs( ): interrogez toutes les informations sur les sommets. 🎜 - 🎜
find_path(fv,tv): Trouvez le chemin d'un sommet à un autre sommet. 🎜
2. Implémentation du stockage graphique
🎜Il existe deux principaux types d'implémentation du stockage graphique : la matrice de contiguïté et la liste de liens. 🎜2.1 Matrice d'adjacence
🎜Utilisez une matrice bidimensionnelle (tableau) pour stocker la relation entre les sommets. 🎜🎜Par exemple,graph[5][5]peut stocker les données relationnelles de 5 sommets. Le numéro de ligne et le numéro de colonne représentent les sommets de la cellule coupant la vème ligne et la wth. La colonne représente le point de départ. Le poids de l'arête du sommet v au sommet w, tel quegrap[2][3]=6signifie que le sommet C2 et le sommet D3 sont connectés (adjacents). , et le poids est 6🎜🎜🎜🎜Avantages des matrices adjacentes C'est simple et peut clairement indiquer que ces sommets sont connectés. Puisque toutes les paires de sommets ne sont pas connectées, il y a beaucoup d’espace inutilisé dans la matrice, souvent appelée « matrice clairsemée ». 🎜🎜La matrice ne sera remplie que lorsque chaque sommet aura une relation avec d'autres sommets. Si la relation entre la structure graphique n'est pas trop complexe, l'utilisation de cette structure pour stocker des données graphiques gaspillera beaucoup d'espace. 🎜🎜La matrice de contiguïté convient pour représenter des structures graphiques avec des relations complexes, telles que les liens entre des pages Web sur Internet et les relations sociales entre les personnes dans les cercles sociaux...🎜2.2 Encodage pour implémenter la matrice de contiguïté
🎜 Étant donné que le sommet lui-même a une signification en matière de données, le type de sommet doit d'abord être défini. 🎜🎜🎜Classe Vertex : 🎜🎜''' 添加节点与节点之间的边， 如果是无权重图，统一设定为 1 ''' def add_edge(self, from_v, to_v): # 如果节点不存在 if from_v not in self.vert_list: self.add_vertex(from_v) if to_v not in self.vert_list: self.add_vertex(to_v) # from_v 节点的编号为行号，to_v 节点的编号为列号 self.matrix[from_v.v_id][to_v.v_id] = 1 ''' 添加有权重的边 ''' def add_edge(self, from_v, to_v, weight): # 如果节点不存在 if from_v not in self.vert_list: self.add_vertex(from_v) if to_v not in self.vert_list: self.add_vertex(to_v) # from_v 节点的编号为行号，to_v 节点的编号为列号 self.matrix[from_v.v_id][to_v.v_id] = weight🎜Dans la classe vertex,v_idetv_namesont faciles à comprendre. Pourquoi ajouter unvisité? 🎜🎜Cette variable est utilisée pour enregistrer si le sommet a été recherché pendant le processus de recherche de chemin afin d'éviter des calculs de recherche répétés. 🎜🎜🎜Classe Graph : 🎜La classe graph a de nombreuses méthodes, nous allons les présenter ici une par une. 🎜🎜🎜Méthode d'initialisation🎜🎜''' 根据节点编号返回节点 ''' def find_vertex(self, v_id): if v_id >= 0 or v_id <= self.v_nums: # 节点编号必须存在 return [tmp_v for tmp_v in self.vert_list if tmp_v.v_id == v_id][0]🎜La méthode d'initialisation est utilisée pour initialiser le type de données dans le graphique : 🎜🎜La liste unidimensionnellevert_listenregistre toutes les données de sommet. 🎜🎜Lamatricede liste bidimensionnelle enregistre les données de relation entre les sommets. 🎜🎜queue_stackUtilisez une liste pour simuler une file d'attente ou une pile pour les recherches ultérieures en largeur et en profondeur. 🎜🎜🎜Comment utiliser une liste pour simuler une file d'attente ou une pile ? 🎜🎜🎜La liste comporte 2 méthodes utiles :append()etpop(). 🎜🎜append()est utilisé pour ajouter des données à la liste, et à chaque fois elle est ajoutée depuis la fin de la liste. 🎜🎜pop()supprime et extrait les données de la fin de la liste par défaut.pop(parameter)peut fournir une valeur d'index pour supprimer et extraire les données de la position spécifiée. . 🎜🎜Utilisez les méthodes append() et pop() pour simuler une pile et saisir et sortir des données au même endroit. 🎜🎜Utilisez les méthodes append() et pop(0) pour simuler une file d'attente, ajouter des données depuis l'arrière et obtenir des données depuis le devant🎜🎜searchPath: utilisé pour enregistrer les données utilisées en largeur ou résultat de la recherche de chemin en profondeur. 🎜🎜🎜Comment ajouter un nouveau point de section (en haut) : 🎜🎜""" 添加新顶点 """ def add_vertex(self, vert): if vert in self.vert_list: # 已经存在 return if self.v_nums >= len(self.matrix): # 超过相邻矩阵所能存储的节点上限 return # 顶点的编号内部生成 vert.v_id = self.v_nums self.vert_list.append(vert) # 数量增一 self.v_nums += 1上述方法注意一点，节点的编号由图内部逻辑提供，便于节点编号顺序的统一。
添加边方法
此方法是邻接矩阵表示法的核心逻辑。
''' 添加节点与节点之间的边， 如果是无权重图，统一设定为 1 ''' def add_edge(self, from_v, to_v): # 如果节点不存在 if from_v not in self.vert_list: self.add_vertex(from_v) if to_v not in self.vert_list: self.add_vertex(to_v) # from_v 节点的编号为行号，to_v 节点的编号为列号 self.matrix[from_v.v_id][to_v.v_id] = 1 ''' 添加有权重的边 ''' def add_edge(self, from_v, to_v, weight): # 如果节点不存在 if from_v not in self.vert_list: self.add_vertex(from_v) if to_v not in self.vert_list: self.add_vertex(to_v) # from_v 节点的编号为行号，to_v 节点的编号为列号 self.matrix[from_v.v_id][to_v.v_id] = weight添加边信息的方法有 2 个，一个用来添加无权重边，一个用来添加有权重的边。
查找某节点
使用线性查找法从节点集合中查找某一个节点。
''' 根据节点编号返回节点 ''' def find_vertex(self, v_id): if v_id >= 0 or v_id <= self.v_nums: # 节点编号必须存在 return [tmp_v for tmp_v in self.vert_list if tmp_v.v_id == v_id][0]查询所有节点
''' 输出所有顶点信息 ''' def find_only_vertexes(self): for tmp_v in self.vert_list: print(tmp_v)此方法仅为了查询方便。
查询节点之间的关系
''' 迭代节点与节点之间的关系（边） ''' def find_vertexes(self): for tmp_v in self.vert_list: edges = self.matrix[tmp_v.v_id] for col in range(len(edges)): w = edges[col] if w != 0: print(tmp_v, '和', self.vert_list[col], '的权重为：', w)测试代码：
if __name__ == "__main__": # 初始化图对象 g = Graph(5) # 添加顶点 for _ in range(len(g.matrix)): v_name = input("顶点的名称（ q 为退出）：") if v_name == 'q': break v = Vertex(v_name) g.add_vertex(v) # 节点之间的关系 infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)] for i in infos: v = g.find_vertex(i[0]) v1 = g.find_vertex(i[1]) g.add_edge(v, v1, i[2]) # 输出顶点及边a print("-----------顶点与顶点关系--------------") g.find_vertexes() ''' 输出结果： 顶点的名称（ q 为退出）：A 顶点的名称（ q 为退出）：B 顶点的名称（ q 为退出）：C 顶点的名称（ q 为退出）：D 顶点的名称（ q 为退出）：E [编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3 [编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5 [编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4 [编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6 [编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1 [编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2 [编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7 '''3. 搜索路径
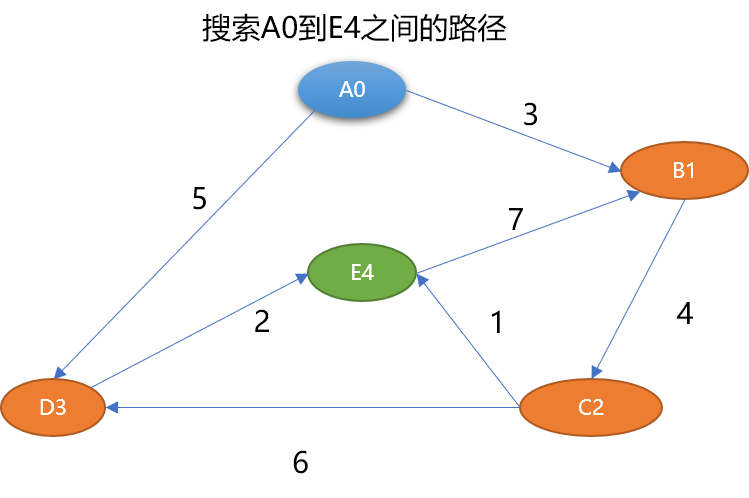
在图中经常做的操作，就是查找从一个顶点到另一个顶点的路径。如怎么查找到 A0 到 E4 之间的路径长度：
从人的直观思维角度查找一下，可以找到如下路径：
{A0，B1，C2，E4}路径长度为 8。{A0，D3，E4}路径长度为 7。{A0，B1，C2，D3，E4}路径长度为 15。
在路径查找时，人的思维具有知识性和直观性特点，因此不存在所谓的尝试或碰壁问题。而计算机是试探性思维，就会出现这条路不通，再找另一条路的现象。
所以路径算法中常常会以错误为代价，在查找过程中会走一些弯路。常用的路径搜索算法有 2 种：
广度优先搜索
深度优先搜索
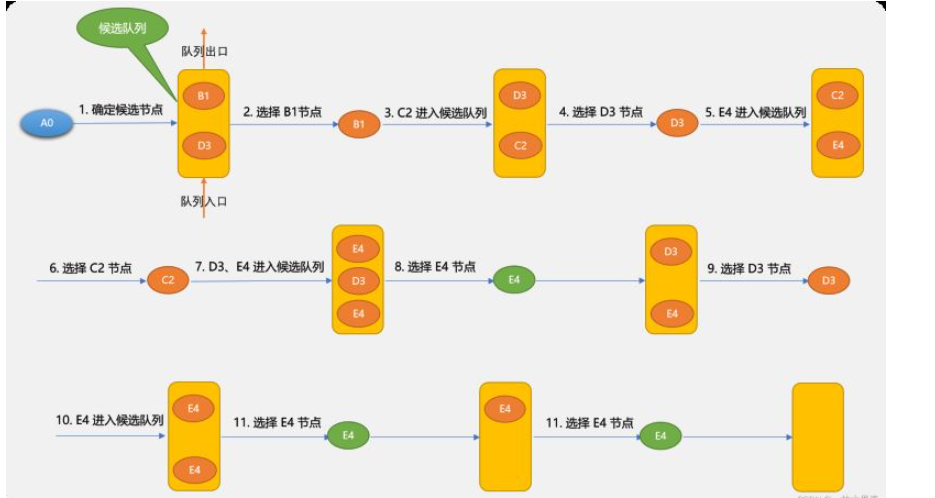
3.1 广度优先搜索
先看一下广度优先搜索的示意图：
广度优先搜索的基本思路：
确定出发点，本案例是 A0 顶点。
以出发点相邻的顶点为候选点，并存储至队列。
从队列中每拿出一个顶点后，再把与此顶点相邻的其它顶点做为候选点存储于队列。
不停重复上述过程，至到找到目标顶点或队列为空。
使用广度搜索到的路径与候选节点进入队列的先后顺序有关系。如第 1 步确定候选节点时
B1和D3谁先进入队列，对于后面的查找也会有影响。上图使用广度搜索可找到
A0~E4路径是：{A0，B1，D3，C2，E4}其实
{A0，B1，C2，E4}也是一条有效路径，有可能搜索不出来，这里因为搜索到B1后不会马上搜索C2，因为B3先于C2进入，广度优先搜索算法只能保证找到路径，而不能保存找到最佳路径。编码实现广度优先搜索：
广度优先搜索需要借助队列临时存储选节点，本文使用列表模拟队列。
在图类中实现广度优先搜索算法的方法：
class Graph(): # 省略其它代码 ''' 广度优先搜索算法 ''' def bfs(self, from_v, to_v): # 查找与 fv 相邻的节点 self.find_neighbor(from_v) # 临时路径 lst_path = [from_v] # 重复条件：队列不为空 while len(self.queue_stack) != 0: # 从队列中一个节点（模拟队列） tmp_v = self.queue_stack.pop(0) # 添加到列表中 lst_path.append(tmp_v) # 是不是目标节点 if tmp_v.v_id == to_v.v_id: self.searchPath.append(lst_path) print('找到一条路径', [v_.v_id for v_ in lst_path]) lst_path.pop() else: self.find_neighbor(tmp_v) ''' 查找某一节点的相邻节点，并添加到队列（栈）中 ''' def find_neighbor(self, find_v): if find_v.visited: return find_v.visited = True # 找到保存 find_v 节点相邻节点的列表 lst = self.matrix[find_v.v_id] for idx in range(len(lst)): if lst[idx] != 0: # 权重不为 0 ，可判断相邻 self.queue_stack.append(self.vert_list[idx])广度优先搜索过程中，需要随时获取与当前节点相邻的节点，
find_neighbor()方法的作用就是用来把当前节点的相邻节点压入队列中。测试广度优先搜索算法：
if __name__ == "__main__": # 初始化图对象 g = Graph(5) # 添加顶点 for _ in range(len(g.matrix)): v_name = input("顶点的名称（ q 为退出）：") if v_name == 'q': break v = Vertex(v_name) g.add_vertex(v) # 节点之间的关系 infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)] for i in infos: v = g.find_vertex(i[0]) v1 = g.find_vertex(i[1]) g.add_edge(v, v1, i[2]) print("----------- 广度优先路径搜索--------------") f_v = g.find_vertex(0) t_v = g.find_vertex(4) g.bfs(f_v,t_v) ''' 输出结果 顶点的名称（ q 为退出）：A 顶点的名称（ q 为退出）：B 顶点的名称（ q 为退出）：C 顶点的名称（ q 为退出）：D 顶点的名称（ q 为退出）：E ----------- 广度优先路径搜索-------------- 找到一条路径 [0, 1, 3, 2, 4] 找到一条路径 [0, 1, 3, 2, 3, 4] '''使用递归实现广度优先搜索算法：
''' 递归方式实现广度搜索 ''' def bfs_dg(self, from_v, to_v): self.searchPath.append(from_v) if from_v.v_id != to_v.v_id: self.find_neighbor(from_v) if len(self.queue_stack) != 0: self.bfs_dg(self.queue_stack.pop(0), to_v)3.2 深度优先搜索算法
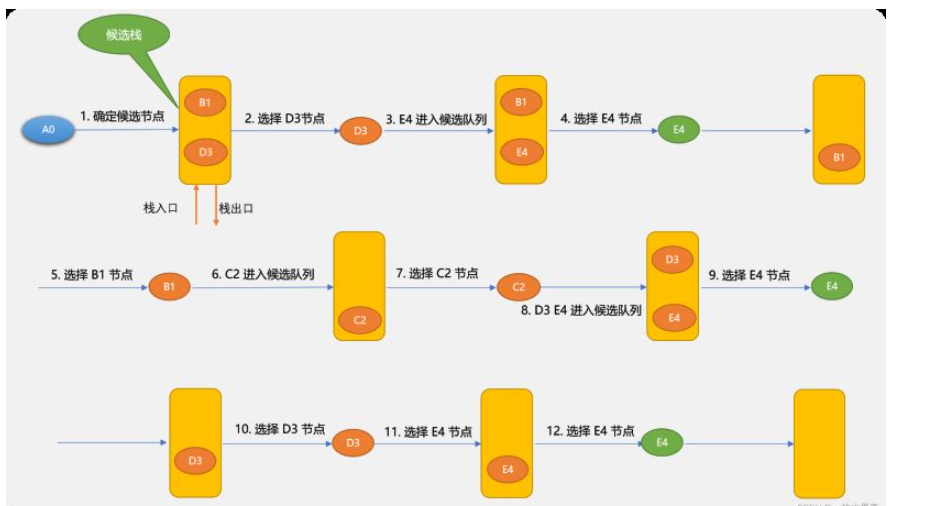
先看一下深度优先算法的示意图。
深度优先搜索算法和广度优先搜索算法不同的地方在于：深度优先搜索算法将候选节点放在堆栈中。因栈是先进后出，所以，搜索到的节点顺序不一样。
使用循环实现深度优先搜索算法：
深度优先搜索算法需要用到栈，本文使用列表模拟。
''' 深度优先搜索算法 使用栈存储下一个需要查找的节点 ''' def dfs(self, from_v, to_v): # 查找与 from_v 相邻的节点 self.find_neighbor(from_v) # 临时路径 lst_path = [from_v] # 重复条件：栈不为空 while len(self.queue_stack) != 0: # 从栈中取一个节点（模拟栈） tmp_v = self.queue_stack.pop() # 添加到列表中 lst_path.append(tmp_v) # 是不是目标节点 if tmp_v.v_id == to_v.v_id: self.searchPath.append(lst_path) print('找到一条路径:', [v_.v_id for v_ in lst_path]) lst_path.pop() else: self.find_neighbor(tmp_v)测试：
if __name__ == "__main__": # 初始化图对象 g = Graph(5) # 添加顶点 for _ in range(len(g.matrix)): v_name = input("顶点的名称（ q 为退出）：") if v_name == 'q': break v = Vertex(v_name) g.add_vertex(v) # 节点之间的关系 infos = [(0, 1, 3), (0, 3, 5), (1, 2, 4), (2, 3, 6), (2, 4, 1), (3, 4, 2), (4, 1, 7)] for i in infos: v = g.find_vertex(i[0]) v1 = g.find_vertex(i[1]) g.add_edge(v, v1, i[2]) # 输出顶点及边a print("-----------顶点与顶点关系--------------") g.find_vertexes() print("----------- 深度优先路径搜索--------------") f_v = g.find_vertex(0) t_v = g.find_vertex(4) g.dfs(f_v, t_v) ''' 输出结果 顶点的名称（ q 为退出）：A 顶点的名称（ q 为退出）：B 顶点的名称（ q 为退出）：C 顶点的名称（ q 为退出）：D 顶点的名称（ q 为退出）：E -----------顶点与顶点关系-------------- [编号为 0，名称为 A ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 3 [编号为 0，名称为 A ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 5 [编号为 1，名称为 B ] 的顶点 和 [编号为 2，名称为 C ] 的顶点 的权重为： 4 [编号为 2，名称为 C ] 的顶点 和 [编号为 3，名称为 D ] 的顶点 的权重为： 6 [编号为 2，名称为 C ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 1 [编号为 3，名称为 D ] 的顶点 和 [编号为 4，名称为 E ] 的顶点 的权重为： 2 [编号为 4，名称为 E ] 的顶点 和 [编号为 1，名称为 B ] 的顶点 的权重为： 7 ----------- 深度优先路径搜索-------------- 找到一条路径: [0, 3, 4] 找到一条路径: [0, 3, 1, 2, 4] '''使用递归实现深度优先搜索算法：
''' 递归实现深度搜索算法 ''' def def_dg(self, from_v, to_v): self.searchPath.append(from_v) if from_v.v_id != to_v.v_id: # 查找与 from_v 节点相连的子节点 lst = self.find_neighbor_(from_v) if lst is not None: for tmp_v in lst[::-1]: self.def_dg(tmp_v, to_v) """ 查找某一节点的相邻节点，以列表方式返回 """ def find_neighbor_(self, find_v): if find_v.visited: return find_v.visited = True # 查找与 find_v 节点相邻的节点 lst = self.matrix[find_v.v_id] return [self.vert_list[idx] for idx in range(len(lst)) if lst[idx] != 0]递归实现时，不需要使用全局栈，只需要获到当前节点的相邻节点便可。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!