Comment utiliser les sept méthodes de tri des structures de données Java

1. Tri par insertion

1. Tri par insertion directe

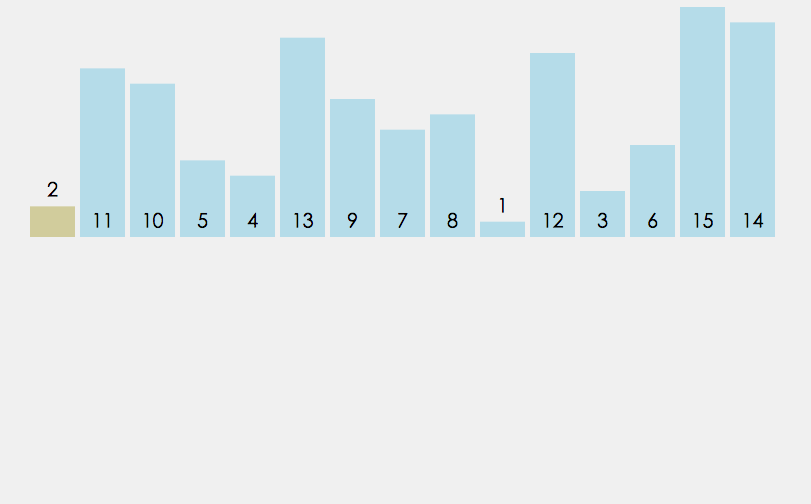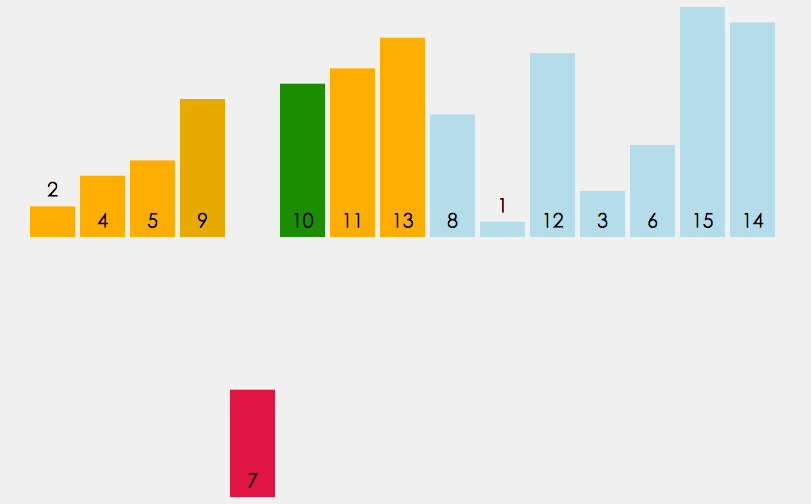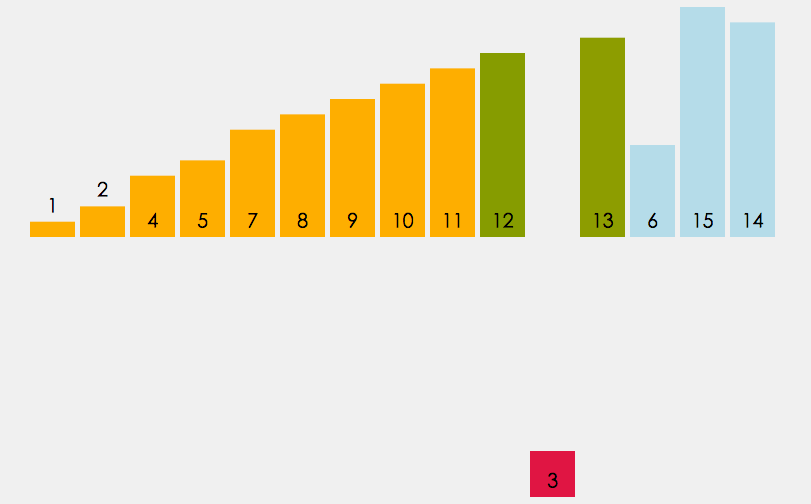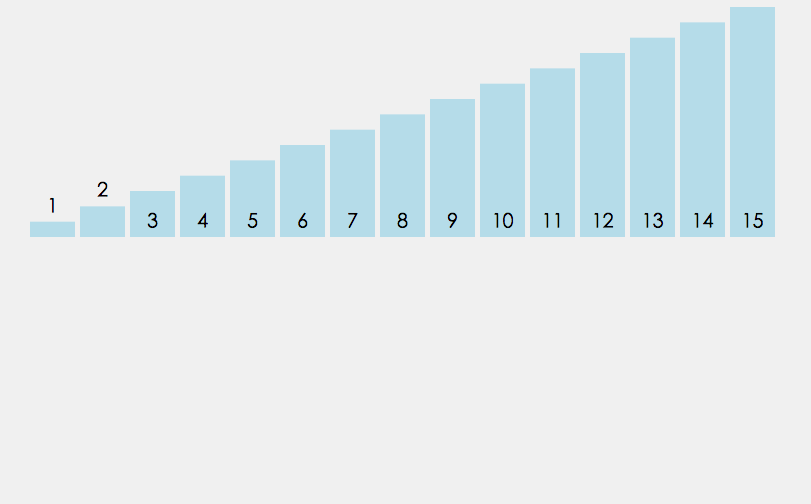
Lors de l'insertion de l'élément i (i>=1), le tableau précédent[0],tableau[1],…,tableau[i -1 ] a été trié. À ce stade, comparez array[i] avec array[i-1], array[i-2],... pour trouver la position d'insertion et insérez array[i]. Reculez dans l’ordre.

Plus les données sont proches de la commande, moins il faut de temps pour insérer directement le tri.

Complexité temporelle : O(N^2)

Complexité spatiale O(1), c'est un algorithme stable

Tri par insertion directe :

    public static void insertSort(int[] array){
        for (int i = 1; i < array.length; i++) {
            int tmp=array[i];
            int j=i-1;
            for(;j>=0;--j){
                if(array[j]>tmp){
                    array[j+1]=array[j];
                }else{
                    break;
                }
            }
            array[j+1]=tmp;
        }
    }

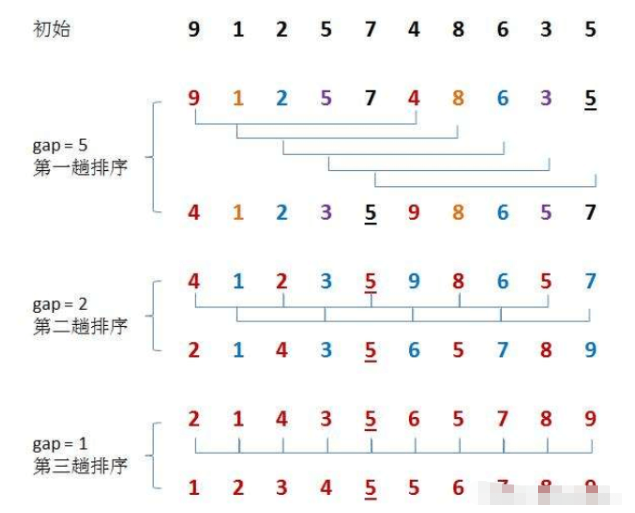
2. ​la méthode est la suivante : sélectionnez d'abord un écart entier, divisez tous les enregistrements du fichier à trier en groupes d'écarts, placez tous les nombres avec une distance d'écart dans le même groupe et effectuez un tri par insertion directe sur les nombres de chaque groupe. . Ensuite, prenez gap=gap/2 et répétez le travail de regroupement et de tri ci-dessus. Lorsque gap=1, tous les nombres sont triés directement au sein d'un groupe.

Le tri Hill est une optimisation du tri par insertion directe.
Le but est de rendre le tableau plus proche de l'ordre, donc le pré-tri est effectué lorsque l'écart > 1. Le tri par insertion peut trier rapidement un tableau presque ordonné lorsque l'écart est de 1.
La complexité temporelle du tri Hill est difficile à calculer car il existe de nombreuses façons de calculer l'écart, ce qui rend le calcul difficile.
Tri par colline :

public static void shellSort(int[] array){
        int size=array.length;
        //这里定义gap的初始值为数组长度的一半
        int gap=size/2;
        while(gap>0){
            //间隔为gap的直接插入排序
            for (int i = gap; i < size; i++) {
                int tmp=array[i];
                int j=i-gap;
                for(;j>=0;j-=gap){
                    if(array[j]>tmp){
                        array[j+gap]=array[j];
                    }else{
                        break;
                    }
                }
                array[j+gap]=tmp;
            }
            gap/=2;
        }
    }

2. Tri par sélection

1 Tri par sélection

Sélectionnez le plus petit élément de données dans le tableau d'ensemble d'éléments[i]--array[n-1]
Si ce n'est pas le premier élément de cet ensemble, échangez-le avec le premier élément de cet ensemble
Dans l'ensemble restant, répétez les étapes ci-dessus jusqu'à ce qu'il reste 1 élément dans l'ensemble
Complexité temporelle : O(N^2)

La complexité spatiale est O(1), instable

Tri par sélection :

    //交换
    private static void swap(int[] array,int i,int j){
        int tmp=array[i];
        array[i]=array[j];
        array[j]=tmp;
    }
    //选择排序
    public static void chooseSort(int[] array){
        for (int i = 0; i < array.length; i++) {
            int minIndex=i;//记录最小值的下标
            for (int j = i+1; j < array.length; j++) {
                if (array[j]<array[minIndex]) {
                    minIndex=j;
                }
            }
            swap(array,i,minIndex);
        }
    }

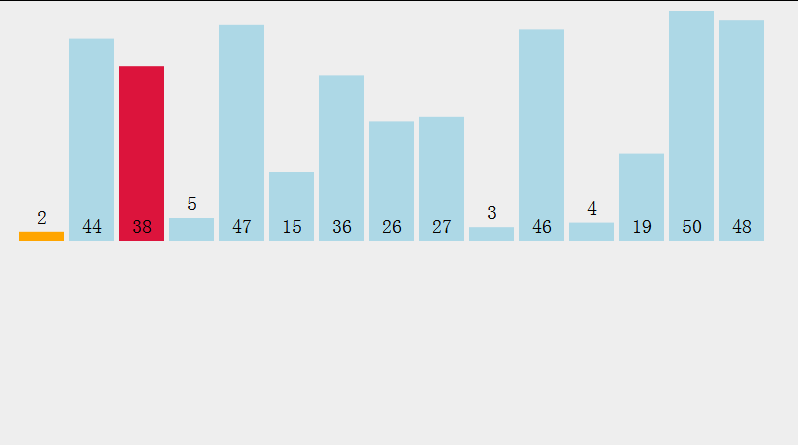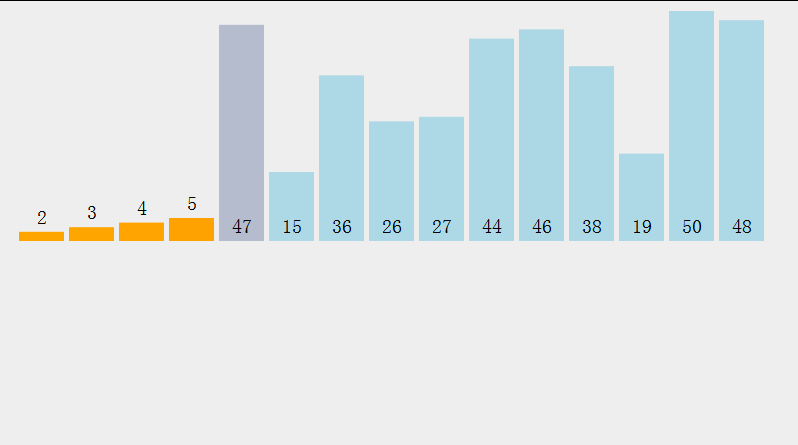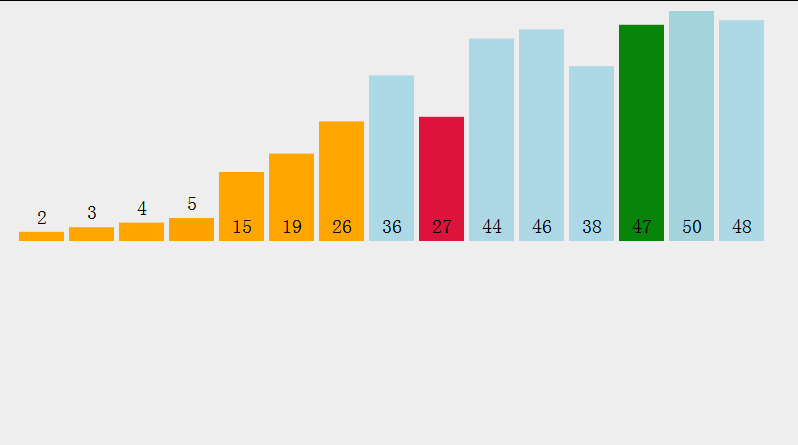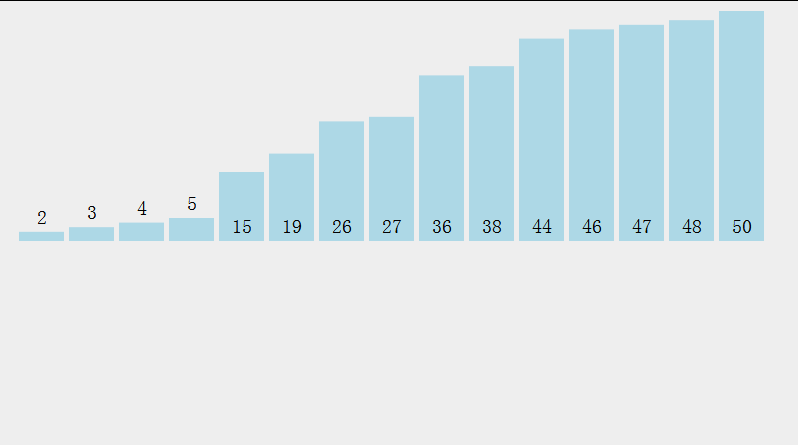2. Tri par tas

Deux idées de tri par tas (en prenant l'ordre croissant comme exemple) :

Créez un petit tas racine, retirez les éléments supérieurs du tas et placez-les tour à tour dans le tableau, jusqu'à ce que le tas soit vide
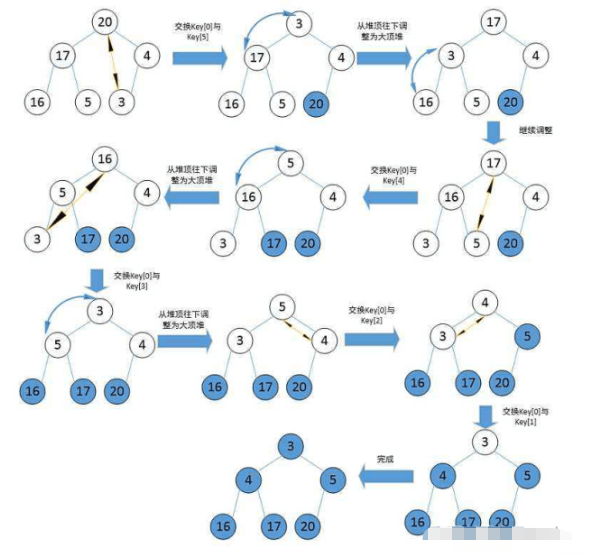
Créez un grand tas racine, définissez la clé de position de l'élément de queue du tas , et échangez le haut du tas à chaque fois L'élément et l'élément à la position clé (key--) jusqu'à ce que la clé atteigne le sommet du tas. À ce moment, le parcours hiérarchique des éléments du tas est ascendant. ordre (comme suit)
Complexité temporelle : O(N^2)

Complexité spatiale : O(N), instable

Tri par tas :

    //向下调整
    public static void shiftDown(int[] array,int parent,int len){
        int child=parent*2+1;
        while(child<len){
            if(child+1<len){
                if(array[child+1]>array[child]){
                    child++;
                }
            }
            if(array[child]>array[parent]){
                swap(array,child,parent);
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
 
        }
    }
    //创建大根堆
    private static void createHeap(int[] array){
        for (int parent = (array.length-1-1)/2; parent >=0; parent--) {
            shiftDown(array,parent,array.length);
        }
    }
    //堆排序
    public static void heapSort(int[] array){
        //创建大根堆
        createHeap(array);
        //排序
        for (int i = array.length-1; i >0; i--) {
            swap(array,0,i);
            shiftDown(array,0,i);
        }
    }

3. Tri par échange

1.

Boucles à deux niveaux, le premier niveau de boucle représente le nombre de fois à trier, et la boucle à deux niveaux représente le nombre de comparaisons à chaque passage ; le tri à bulles a ici été optimisé lors de chaque comparaison. peut définir un compteur pour enregistrer le nombre d'échanges de données. S'il n'y a pas d'échange, cela signifie que les données sont en ordre. Plus besoin de tri.

Complexité temporelle : O(N^2)

La complexité spatiale est O(1), qui est un tri stable

Tri à bulles :

   public static void bubbleSort(int[] array){
        for(int i=0;i<array.length-1;++i){
            int count=0;
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j]>array[j+1]){
                    swap(array,j,j+1);
                    count++;
                }
            }
            if(count==0){
                break;
            }
        }
    }

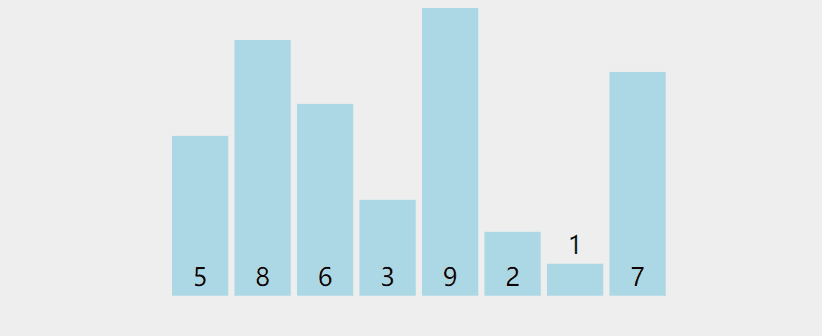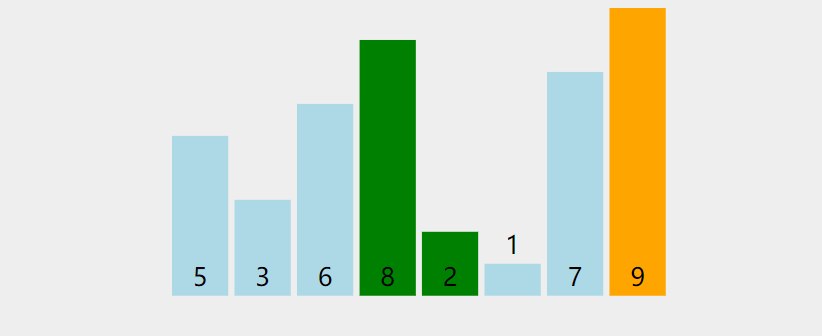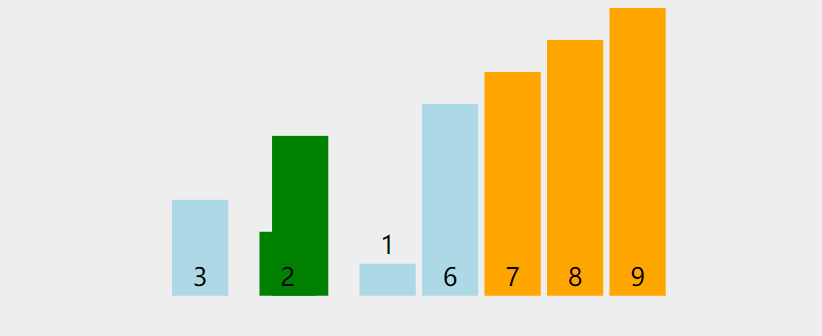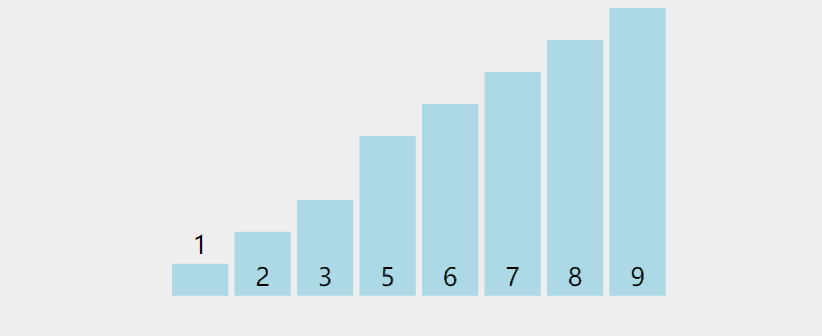Tri rapide

Tout choix à trier Un certain. L'élément de la séquence d'éléments est utilisé comme valeur de référence. Selon ce code de tri, l'ensemble à trier est divisé en deux sous-séquences. Tous les éléments de la sous-séquence de gauche sont inférieurs à la valeur de référence et tous les éléments de la sous-séquence de droite le sont. supérieure à la valeur de référence. Ensuite, la sous-séquence la plus à gauche. La séquence répète ce processus jusqu'à ce que tous les éléments soient disposés dans leurs positions correspondantes.

Complexité temporelle : Meilleur O(n*logn) : La séquence à trier peut être divisée aussi uniformément que possible à chaque fois

                      Pire O(N^2) : La séquence à trier elle-même est ordonnée

Complexité spatiale : O(logn) au mieux, O(N) au pire. Tri instable

(1) Méthode de fouille

Lorsque les données sont ordonnées, le tri rapide équivaut à un arbre binaire sans sous-arbres gauche ou droit. À ce moment, la complexité spatiale atteindra O(N). quantité de données Le tri peut provoquer un débordement de pile.

public static void quickSort(int[] array,int left,int right){
        if(left>=right){
            return;
        }
        int l=left;
        int r=right;
        int tmp=array[l];
        while(l<r){
            while(array[r]>=tmp&&l<r){
            //等号不能省略，如果省略，当序列中存在相同的值时，程序会死循环
                r--;
            }
            array[l]=array[r];
            while(array[l]<=tmp&&l<r){
                l++;
            }
            array[r]=array[l];
        }
        array[l]=tmp;
        quickSort(array,0,l-1);
        quickSort(array,l+1,right);
    }

(2) Optimisation du tri rapide

Choisissez la clé en prenant le milieu de trois nombres

Concernant la sélection des valeurs clés, si la séquence à trier est dans l'ordre, alors on sélectionne la première ou la dernière selon la clé qui peut conduire à une segmentation Le côté gauche ou droit de est vide. Dans ce cas, la complexité spatiale du tri rapide sera relativement grande, ce qui peut facilement provoquer un débordement de pile. Nous pouvons alors utiliser la méthode des trois nombres pour annuler cette situation. La valeur médiane du premier, du dernier et du milieu des éléments de la séquence est utilisée comme valeur clé.

 //key值的优化，只在快速排序中使用，则可以为private
    private int threeMid(int[] array,int left,int right){
        int mid=(left+right)/2;
        if(array[left]>array[right]){
            if(array[mid]>array[left]){
                return left;
            }
            return array[mid]<array[right]?right:mid;
        }else{
            if(array[mid]<array[left]){
                return left;
            }
            return array[mid]>array[right]?right:mid;
        }
    }

Lors d'une récursion dans une petite sous-plage, vous pouvez envisager d'utiliser le tri par insertion

随着我们递归的进行，区间会变的越来越小，我们可以在区间小到一个值的时候，对其进行插入排序，这样代码的效率会提高很多。

（3）快速排序的非递归实现

 //找到一次划分的下标
    public static int patition(int[] array,int left,int right){
        int tmp=array[left];
        while(left<right){
            while(left<right&&array[right]>=tmp){
                right--;
            }
            array[left]=array[right];
            while(left<right&&array[left]<=tmp){
                left++;
            }
            array[right]=array[left];
        }
        array[left]=tmp;
        return left;
    }
    //快速排序的非递归
    public static void quickSort2(int[] array){
        Stack<Integer> stack=new Stack<>();
        int left=0;
        int right=array.length-1;
        stack.push(left);
        stack.push(right);
        while(!stack.isEmpty()){
            int r=stack.pop();
            int l=stack.pop();
            int p=patition(array,l,r);
            if(p-1>l){
                stack.push(l);
                stack.push(p-1);
            }
            if(p+1<r){
                stack.push(p+1);
                stack.push(r);
            }
        }
    }

四、归并排序

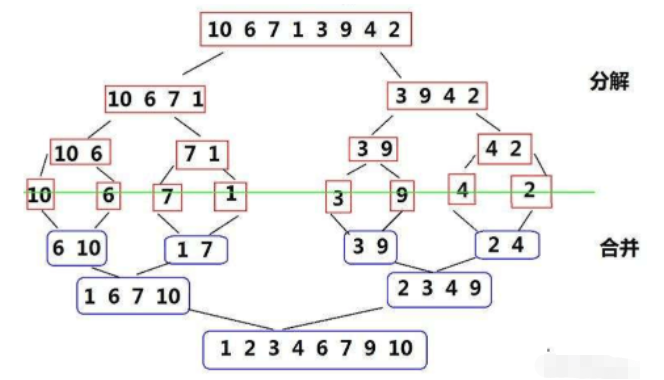
归并排序（MERGE-SORT）：该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。实现序列的完全有序，需要将已经有序的子序列合并，即先让每个子序列有序，然后再将相邻的子序列段有序。若将两个有序表合并成一个有序表，称为二路归并。

时间复杂度：O(n*logN)（无论有序还是无序）

空间复杂度：O（N）。是稳定的排序。

    //归并排序：递归
    public static void mergeSort(int[] array,int left,int right){
        if(left>=right){
            return;
        }
        int mid=(left+right)/2;
        //递归分割
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);
        //合并
        merge(array,left,right，mid);
    }
    //非递归
    public static void mergeSort1(int[] array){
        int gap=1;
        while(gap<array.length){
            for (int i = 0; i < array.length; i+=2*gap) {
                int left=i;
                int mid=left+gap-1;
                if(mid>=array.length){
                    mid=array.length-1;
                }
                int right=left+2*gap-1;
                if(right>=array.length){
                    right=array.length-1;
                }
                merge(array,left,right,mid);
            }
            gap=gap*2;
        }
    } 
    //合并：合并两个有序数组
    public static void merge(int[] array,int left,int right，int mid){
        int[] tmp=new int[right-left+1];
        int k=0;
        int s1=left;
        int e1=mid;
        int s2=mid+1;
        int e2=right;
        while(s1<=e1&&s2<=e2){
            if(array[s1]<=array[s2]){
                tmp[k++]=array[s1++];
            }else{
                tmp[k++]=array[s2++];
            }
        }
        while(s1<=e1){
            tmp[k++]=array[s1++];
        }
        while(s2<=e2){
            tmp[k++]=array[s2++];
        }
        for (int i = left; i <= right; i++) {
            array[i]=tmp[i-left];
        }
    }

五、排序算法的分析

排序方法	最好时间复杂度	最坏时间复杂度	空间复杂度	稳定性
直接插入排序	O(n)	O(n^2)	O(1)	稳定
希尔排序	O(n)	O(n^2)	O(1）	不稳定
直接排序	O(n^2)	O(n^2)	O(1)	不稳定
堆排序	O(nlog(2)n)	O(nlog(2)n)	O(1)	不稳定
冒泡排序	O(n)	O(n^2)	O(1)	稳定
快速排序	O(nlog(2)n)	O(n^2)	O(nlog(2)n)	不稳定
归并排序	O(nlog(2)n)	O(nlog(2)n)	O(n)	稳定

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!