Comment implémenter le tri topologique en Java

Préparer

Dans cette section, nous présenterons les algorithmes liés aux graphes orientés, nous expliquerons donc d'abord certains concepts de graphes orientés ; les articles suivants n'expliqueront pas ces concepts en détail ; Premièrement, les nœuds du graphe orienté sont reliés par des lignes avec des flèches. Le degré extérieur et le degré intérieur d'un nœud peuvent être utilisés pour le décrire. Lorsque la queue d'une connexion pointe vers le nœud, son degré extérieur augmentera de 1 et lorsque la flèche d'une connexion pointe vers le nœud, son degré augmentera de 1. Regardez l'exemple suivant, A a un degré d'entrée de 0 et un degré de sortie de 2, B a un degré d'entrée de 1 et un degré de sortie de 1, C a un degré d'entrée de 1 et un degré de sortie. degré de 1, D a un degré d'entrée de 2 et un degré de sortie est de 0.

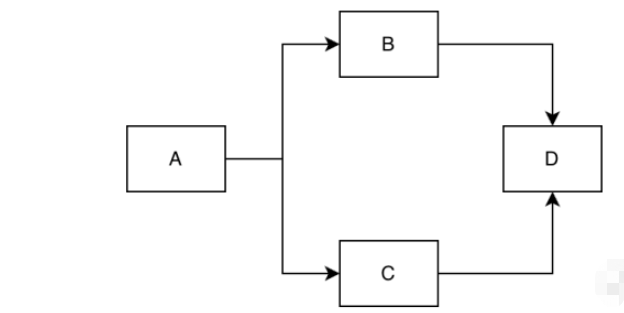
Liste de contiguïté : La liste de contiguïté est un moyen efficace de stocker la structure du graphique. Comme le montre la figure ci-dessous, le tableau de nœuds de gauche stocke tous les nœuds du graphique et la liste de contiguïté de droite stocke. les nœuds adjacents du nœud.

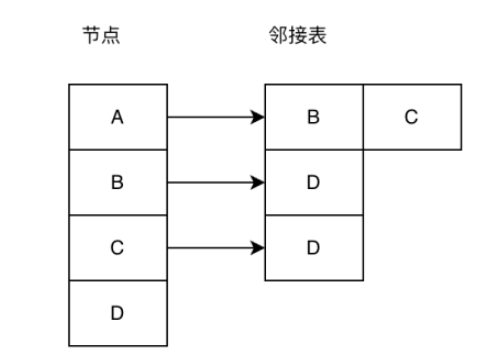
Introduction

Dans cet article, nous allons parler du tri topologique, qui est un algorithme pour les graphes acycliques dirigés. Il est principalement utilisé pour résoudre la relation entre prédécesseur et successeur, c'est-à-dire lorsque nous complétons le courant. tâche, nous devons d'abord Quelles tâches sont accomplies ? En fait, cela est beaucoup utilisé dans notre contrôle de processus. En regardant l'image ci-dessous, nous devons d'abord terminer l'élément A, puis nous pouvons compléter les éléments B et C. Les questions B et C sont parallèles et non dans l'ordre, mais l'élément D ne peut être complété qu'une fois les éléments B et C terminés. Le tri topologique peut nous aider à trouver un ordre raisonnable pour terminer les éléments. En même temps, regardons l'exemple ci-dessus. Une fois l'élément A terminé, les éléments B et C ne sont pas dans l'ordre. les conditions sont remplies, donc tri topologique La séquence d'ordre n'est pas complètement certaine.

Processus de travail

Tout d'abord, le tri topologique correspond à un graphe acyclique orienté. Pour un graphe acyclique, il doit y avoir au moins un nœud avec un degré 0. Dans la situation actuelle, nous devons trouver un nœud avec un degré d'entrée de 0 pour fonctionner. Un degré d'entrée de 0 signifie que le nœud actuel n'a pas de nœud prédécesseur, ou que le nœud prédécesseur a été traité et peut être utilisé directement. Une fois l'opération terminée, tous les nœuds successeurs du nœud actuel sont réduits de 1 et le nœud avec un nœud en degré de 0 est à nouveau recherché pour l'opération. Après cela, il s'agit d'un processus récursif. et les nœuds avec un degré d'entrée de 0 dans la situation actuelle sont traités en continu jusqu'à ce que tous les nœuds soient traités.

Structure des données

Ce qui suit est la structure d'un graphe orienté, où node stocke tous les nœuds du graphe actuel et adj stocke les points adjacents correspondant aux nœuds indicés. Lors de l'initialisation du graphique, vous devez spécifier le nombre de nœuds, créer un tableau de nœuds et un tableau de contiguïté. Fournit une méthode nommée addEdge, qui est utilisée pour établir une limite entre deux nœuds, c'est-à-dire pour ajouter le nœud successeur à la liste de contiguïté du nœud prédécesseur.

public static class Graph{
       /**
        * 节点个数
        */
       private Integer nodeSize;
       /**
        * 节点
        */
       private char[] node;
       /**
        * 邻接表
        */
       private LinkedList[] adj;

       public Graph(char[] node) {
           this.nodeSize = node.length;
           this.node = node;
           this.adj = new LinkedList[nodeSize];
           for (int i = 0 ; i < adj.length ; i++) {
               adj[i] = new LinkedList();
          }
      }
       /**
        * 在节点之间加边，前驱节点指向后继节点
        * @param front 前驱节点所在下标
        * @param end 后继节点所在下标
        */
       public void addEdge(int front, int end) {
           adj[front].add(end);
      }
  }

Tri topologique

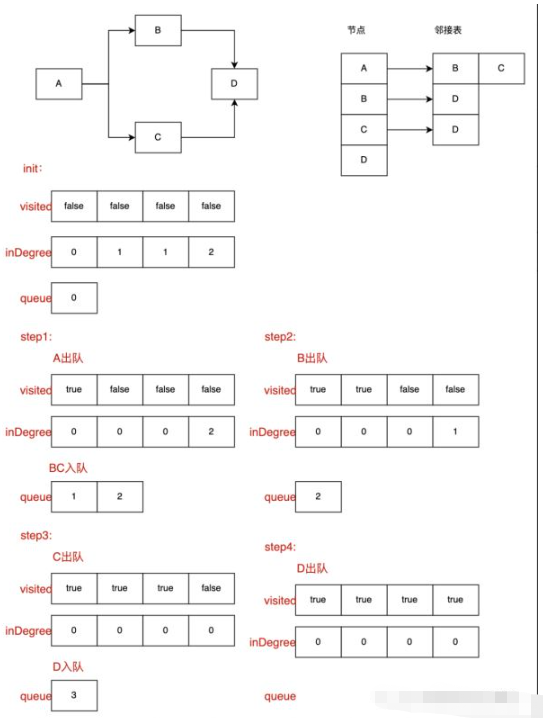
Le tri topologique initialise d'abord deux tableaux temporaires, une file d'attente et un tableau inDegree pour stocker le degré en du nœud d'indice correspondant, car chaque nœud accédé nécessite que le nœud prédécesseur soit terminé, c'est-à-dire le degré d'entrée est 0, avec ce tableau, nous pouvons trouver ces nœuds relativement rapidement ; l'autre est le tableau visité, qui marque si le nœud actuel a été visité pour éviter plusieurs visites ; degré de 0 dans la situation actuelle. (Notez que pour faciliter l'accès, nous stockons tous les indices de nœuds. Étape 1 : initialisez le tableau inDegree et le tableau visité ; étape 2 : parcourez le tableau inDegree et placez tous les nœuds avec un indegree de 0 dans la file d'attente des nœuds ; étape 3 : quittez le nœud. nœuds dans la file d'attente ; Déterminer si le nœud actuel a été visité en fonction de la visite, si oui, revenir à l'étape 3, sinon, passer à l'étape suivante : définir le degré d'entrée du nœud adjacent du nœud actuel sur -1 ; , déterminez si le degré entrant du nœud adjacent est 0, s'il est 0, placez-le directement dans la file d'attente des nœuds, s'il n'est pas 0, revenez à l'étape 3

/**
    * @param graph 有向无环图
    * @return 拓扑排序结果
    */
   public List<Character> toPoLogicalSort(Graph graph) {
       //用一个数组标志所有节点入度
       int[] inDegree = new int[graph.nodeSize];
       for (LinkedList list : graph.adj) {
           for (Object index : list) {
               ++ inDegree[(int)index];
          }
      }
       //用一个数组标志所有节点是否已经被访问
       boolean[] visited = new boolean[graph.nodeSize];
       //开始进行遍历
       Deque<Integer> nodes = new LinkedList<>();
       //将入度为0节点入队
       for (int i = 0 ; i < graph.nodeSize; i++) {
           if (inDegree[i] == 0) {
               nodes.offer(i);
          }
      }
       List<Character> result = new ArrayList<>();
       //将入度为0节点一次出队处理
       while (!nodes.isEmpty()) {
           int node = nodes.poll();
           if (visited[node]) {
               continue;
          }
           visited[node] = true;
           result.add(graph.node[node]);
           //将当前node的邻接节点入度-1；
           for (Object list : graph.adj[node]) {
               -- inDegree[(int)list];
               if (inDegree[(int)list] == 0) {
                   //前驱节点全部访问完毕，入度为0
                   nodes.offer((int) list);
              }
          }
      }
       return result;
  }

Échantillon de test 1

public static void main(String[] args) {
       ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
       //初始化一个图
       Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D'});
       graph.addEdge(0, 1);
       graph.addEdge(0,2);
       graph.addEdge(1,3);
       graph.addEdge(2,3);
       List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
  }

Résultat de l'exécution ;

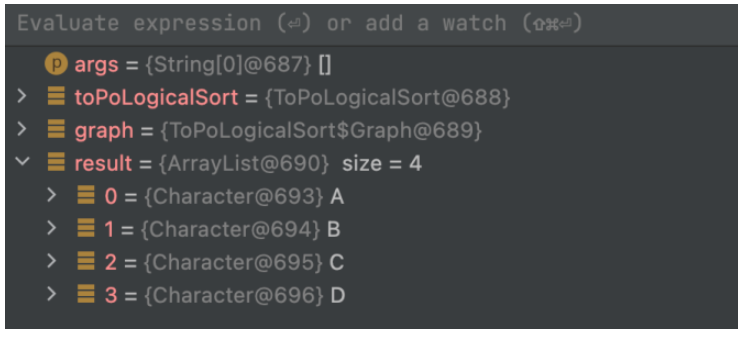
Échantillon de test 2

public static void main(String[] args) {
       ToPoLogicalSort toPoLogicalSort = new ToPoLogicalSort();
       //初始化一个图
       Graph graph = new Graph(new char[]{'A', 'B', 'C', 'D','E','F','G','H'});
       graph.addEdge(0, 1);
       graph.addEdge(0,2);
       graph.addEdge(0,3);
       graph.addEdge(1,4);
       graph.addEdge(2,4);
       graph.addEdge(3,4);
       graph.addEdge(4,7);
       graph.addEdge(4,6);
       graph.addEdge(7,5);
       graph.addEdge(6,7);
       List<Character> result = toPoLogicalSort.toPoLogicalSort(graph);
  }

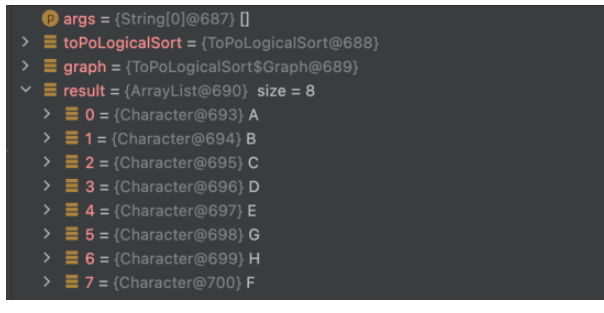
Résultat d'exécution

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!