Maison >Java >javaDidacticiel >Comment implémenter l'algorithme Kruskal en Java
Comment implémenter l'algorithme Kruskal en Java
- 王林avant
- 2023-05-11 22:19:04928parcourir
Introduction
Il existe un autre algorithme pour construire un arbre couvrant minimum, à savoir l'algorithme de Kruskal : Soit le graphe G=(V, E) un graphe pondéré connecté non orienté, V={1,2,...n} ; l'arbre couvrant minimum Tree T = (V, TE), l'état initial de l'arbre est un graphe non connecté avec seulement n nœuds et aucune arête T = (V, {}). L'algorithme de Kruskal traite ces n nœuds comme n isolés. branches connectées. Il trie d'abord toutes les arêtes en fonction de leurs poids de petit à grand, puis si le nombre d'arêtes à sélectionner dans T est inférieur à n-1, il effectue une sélection gourmande comme celle-ci : sélectionne l'arête (i,j) avec le plus petit poids dans l'ensemble d'arêtes E ), si l'ajout d'arête (i, j) à l'ensemble TE ne produit pas de cycle, alors ajoutez l'arête (i, j) à l'ensemble d'arêtes TE, c'est-à-dire utilisez l'arête (i , j) pour fusionner les deux branches en une branche connectée ; Sinon, continuez à sélectionner le bord le plus court suivant. Supprimez l'arête (i, j) de l'ensemble E et continuez la sélection gourmande ci-dessus jusqu'à ce que tous les nœuds de T soient sur la même branche connectée. A cet instant, les n-1 arêtes sélectionnées constituent exactement un arbre couvrant minimum T du graphe G.
L'algorithme de Kruskal utilise une méthode très intelligente, qui consiste à utiliser des ensembles pour éviter les cercles ; si le point de départ et le point final de l'arête sélectionnée à joindre sont tous deux dans l'ensemble T, on peut conclure qu'une boucle sera formée, et les deux nœuds modifiés ne peuvent pas appartenir au même ensemble.
Étapes de l'algorithme
1 Initialisation. Triez toutes les arêtes par ordre croissant de poids et initialisez chaque numéro d'ensemble de nœuds avec son propre numéro.
2 Sélectionnez le bord (u, v) avec le plus petit poids dans l'ordre de tri.
3 Si les nœuds u et v appartiennent à deux branches connectées différentes, ajoutez l'arête (u, v) à l'ensemble d'arêtes TE et fusionnez les deux branches connectées.
4 Si le nombre d'arêtes sélectionnées est inférieur à n-1, passez à l'étape 2, sinon l'algorithme se termine.
1. L'image construite
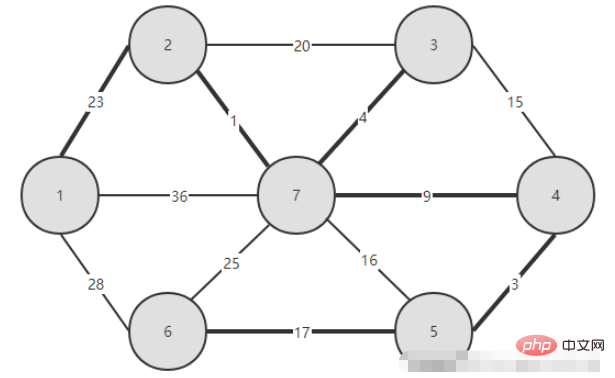
2. Code
package graph.kruskal;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
public class Kruskal {
static final int N = 100;
static int fa[] = new int[N];
static int n;
static int m;
static Edge e[] = new Edge[N * N];
static List<Edge> edgeList = new ArrayList();
static {
for (int i = 0; i < e.length; i++) {
e[i] = new Edge();
}
}
// 初始化集合号为自身
static void Init(int n) {
for (int i = 1; i <= n; i++)
fa[i] = i;
}
// 合并
static int Merge(int a, int b) {
int p = fa[a];
int q = fa[b];
if (p == q) return 0;
for (int i = 1; i <= n; i++) { // 检查所有结点,把集合号是 q 的改为 p
if (fa[i] == q)
fa[i] = p; // a 的集合号赋值给 b 集合号
}
return 1;
}
// 求最小生成树
static int Kruskal(int n) {
int ans = 0;
Collections.sort(edgeList);
for (int i = 0; i < m; i++)
if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
ans += edgeList.get(i).w;
n--;
if (n == 1)//n-1次合并算法结束
return ans;
}
return 0;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
Init(n);
for (int i = 1; i <= m; i++) {
e[i].u = scanner.nextInt();
e[i].v = scanner.nextInt();
e[i].w = scanner.nextInt();
edgeList.add(e[i]);
}
System.out.println("最小的花费是:" + Kruskal(n));
}
}
class Edge implements Comparable {
int u;
int w;
int v;
@Override
public int compareTo(Object o) {
if (this.w > ((Edge) o).w) {
return 1;
} else if (this.w == ((Edge) o).w) {
return 0;
} else {
return -1;
}
}
}3.Le vert est l'entrée et le blanc est la sortie.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

