Maison >développement back-end >Tutoriel Python >Comment utiliser Python pour trouver la norme et le déterminant d'une matrice
Comment utiliser Python pour trouver la norme et le déterminant d'une matrice
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-05-10 23:10:061477parcourir
Dans la fonction de scipy.linalg, deux paramètres sont souvent fournis. L'un est check_finite. Lorsqu'il est True, une vérification limitée sera. effectué , l'autre type est overwrite_xxxx, qui indique si xxxx peut être écrasé pendant le processus de calcul. Par souci de simplicité, nous dirons plus tard que a fournit un commutateur d'écrasement, ce qui signifie qu'il existe un paramètre overwrite_a lorsqu'il est Truecode>, a permet que le processus de calcul soit remplacé ; si un commutateur de vérification limité est fourni, cela signifie que le paramètre <code>check_finite est fourni. scipy.linalg的函数中,往往会提供两种参数,其一是check_finite,当为True时将进行有限检查,另一类是overwrite_xxxx,表示xxxx在计算过程中是否可以被覆写。简洁起见,后文中说a提供覆写开关,就表示存在一个参数overwrite_a,当其为True时,a允许计算过程中被覆写;若说提供有限检查开关,则代表提供check_finite参数。
范数
在scipy.linalg中提供了函数norm用来求范数,其定义为
norm(a, ord=None, axis=None, keepdims=False, check_finite=True)
其中ord用于声明范数的阶
| ord | 矩阵范数 | 向量范数 |
|---|---|---|
| None | 弗罗贝尼乌斯范数 | 2-范数 |
'fro' |
弗罗贝尼乌斯范数 | - |
'nuc' |
核范数 | - |
| inf | max(sum(abs(a), axis=1)) |
max ( ∣ a ∣ ) |
| -inf | min(sum(abs(a), axis=1)) |
min ( ∣ a ∣ ) |
| 0 | - | sum(a!=0) |
| 1 | max(sum(abs(a), axis=0)) |
|
| -1 | min(sum(abs(a), axis=0)) |
|
| 2 | 2-范数(最大奇异值) | |
| -2 | 最小奇异值 |
若a为向量,若ord为非零整数,记作n nn,设a i a_iai为矩阵a aa中的元素,则矩阵的n nn范数为
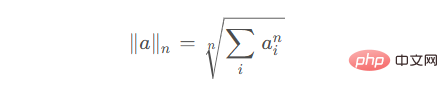
核范数又称“迹范数” (trace norm),表示矩阵的所有奇异值之和。
Frobenius范数可定义为
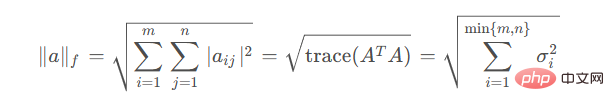
其实质是向量的2-范数在矩阵中的自然推广。
除了scipy.linalg之外,numpy.linalg中也提供了norm,其参数为
norm(x, ord=None, axis=None, keepdims=False)
其中order的可选参数与scipy.linalg中的norm函数相同。
行列式
在scipy.linalg中,行列式函数为det,其定义非常简单,除了待求矩阵a之外,就只有a的覆写开关和有限检查。
示例如下
import numpy as np from scipy import linalg a = np.array([[1,2,3], [4,5,6], [7,8,9]]) linalg.det(a) # 0.0 a = np.array([[0,2,3], [4,5,6], [7,8,9]]) linalg.det(a) # 3.0
迹
scipy.linalg不提供trace函数,但是numpy提供,其定义为
umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)
其中
offset为偏移量,表示相对于主对角线的偏移axis1, axis2表示坐标轴-
dtypeNorm
La fonctionnormest fournie dansscipy.linalgpour trouver la norme, qui est définie comme
>>> x = np.random.rand(3,3) >>> print(x) [[0.26832187 0.64615363 0.09006217] [0.63106319 0.65573765 0.35842304] [0.66629322 0.16999836 0.92357658]] >>> np.trace(x) 1.8476361016546932où
ord est utilisé pour déclarer l'ordre de la norme 🎜| ord | Norme matricielle | Norme vectorielle Numéro |
|---|---|---|
|
td> |
||
| Aucun | Norme Frobenius | Norme 2 |
'fro' |
Norme Frobenius | - |
'nuc' |
Norme nucléaire | - |
| inf | max(sum( abs(a), axis=1)) |
max ( ∣ a ∣ ) |
| -inf | min(somme(abs(a), axis=1)) |
min ( ∣ a ∣ ) |
| 0 | - | somme(a!=0) | tr>
| 1 |
td> |
|
| -1 | min(sum(abs(a), axis=0)) |
|
| 2 | 2-norme (valeur singulière maximale) | |
| -2 | Valeur singulière minimale |
a est un vecteur Si numpy.linalg fournit également norm, dont les paramètres sont 🎜rrreee🎜où order L'optionnel les paramètres de sont les mêmes que ceux de la fonction norm dans scipy.linalg. 🎜Déterminant
🎜Dansscipy.linalg, la fonction déterminante est det, et sa définition est très simple, à l'exception de la matrice à trouver a En dehors de , il n'y a que des commutateurs de remplacement et des vérifications limitées de a. 🎜🎜L'exemple est le suivant🎜rrreeetrace
🎜scipy.linalg ne fournit pas la fonction trace, mais numpy fait, et sa définition est 🎜rrreee🎜où 🎜- 🎜
offsetest le décalage, indiquant le décalage par rapport à la diagonale principale 🎜🎜 - 🎜
axis1, axis2représente l'axe des coordonnées🎜🎜 - 🎜
dtypeest le type de données utilisé pour ajuster la valeur de sortie🎜🎜🎜rrreee
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

