Comment trier 100 millions de nombres aléatoires en Java ?

1. Tri par insertion directe

1. Tri par insertion illustré

Idée : Littéralement, l'insertion consiste à placer un élément dans un ensemble spécifique selon une certaine règle, nous devons donc diviser la séquence en deux parties, une partie. est un ensemble ordonné, et l'autre partie est l'ensemble à trier

Illustration :

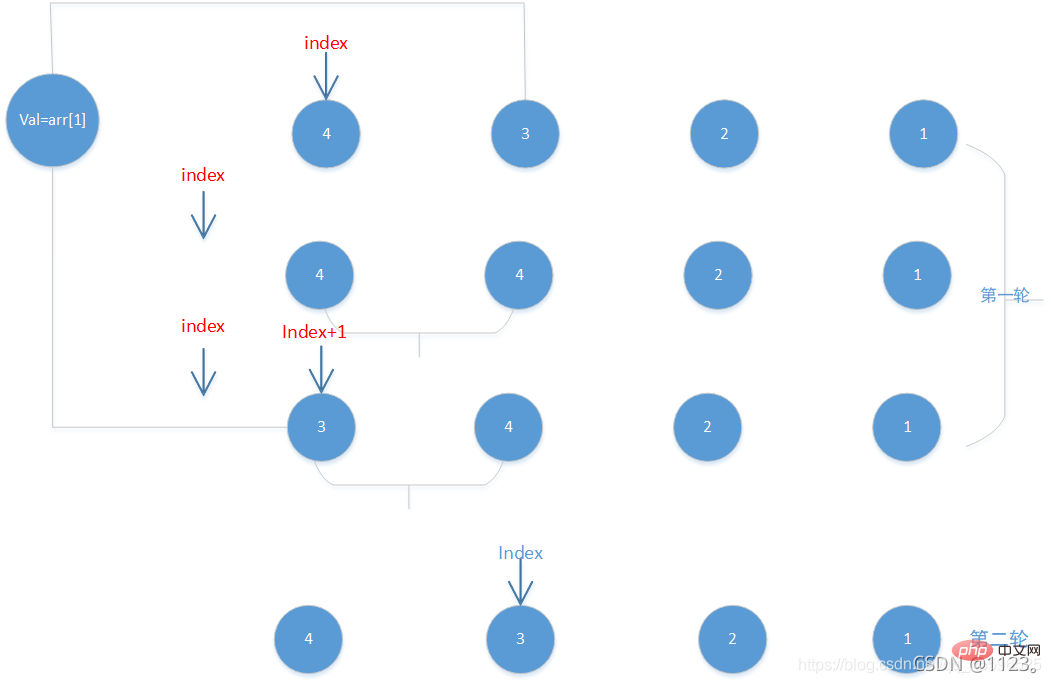
Afin de faciliter la compréhension, nous prendrons comme exemple la séquence 4321 la plus spéciale.

D'après ce qui précède idées, nous devons convertir la séquence divisée en deux parties, pour la commodité du codage, nous supposons que le premier élément est un ensemble ordonné, alors notre boucle devrait commencer à partir du 2ème élément , qui est 3

pour éviter l'écrasement 3 dans les opérations suivantes, nous choisissons une variable temporaire pour enregistrer 3. C'est ce qui précède val=arr[1] ,val=arr[1] ,

由于是对数组继进行操作 , 我们同时也需要获取有序集合的最后一个元素的索引作为游标

当游标不越界 , 且待插入的值小于游标指示位置时(上图的4) , 我们将元素4后移 , 游标前移,继续检查集合中的其它元素是否也小于待插入的元素, 直到游标越界

上图由于集合内只有一个4, 游标前移越界了, 因此循环终止. 下一轮比较开始执行

2. 代码实现

public static void insertSort(int[]arr){
        for(int i = 1 ; i < arr.length; i++){
            int val = arr[i];
            int valIndex = i - 1; //游标
            while(valIndex >= 0 && val < arr[valIndex]){ //插入的值比游标指示的值小
                arr[valIndex + 1] = arr[valIndex];
                valIndex--; //游标前移
            }
            arr[valIndex+1] = val;
        }
    }
1234567891011

3.性能检测与时空复杂度

实际运行80w个数据耗时1分4秒(非准确值,每台机器可能都不一样)

直接插排在排序记录较少, 关键字基本有序的情况下效率较高

时间复杂度 :

关键字比较次数 : KCN=(n^2)/2 总移动次数 : RMN= (n^2)/2

因此时间复杂度约为 O(N^2)

二、希尔排序(交换法)

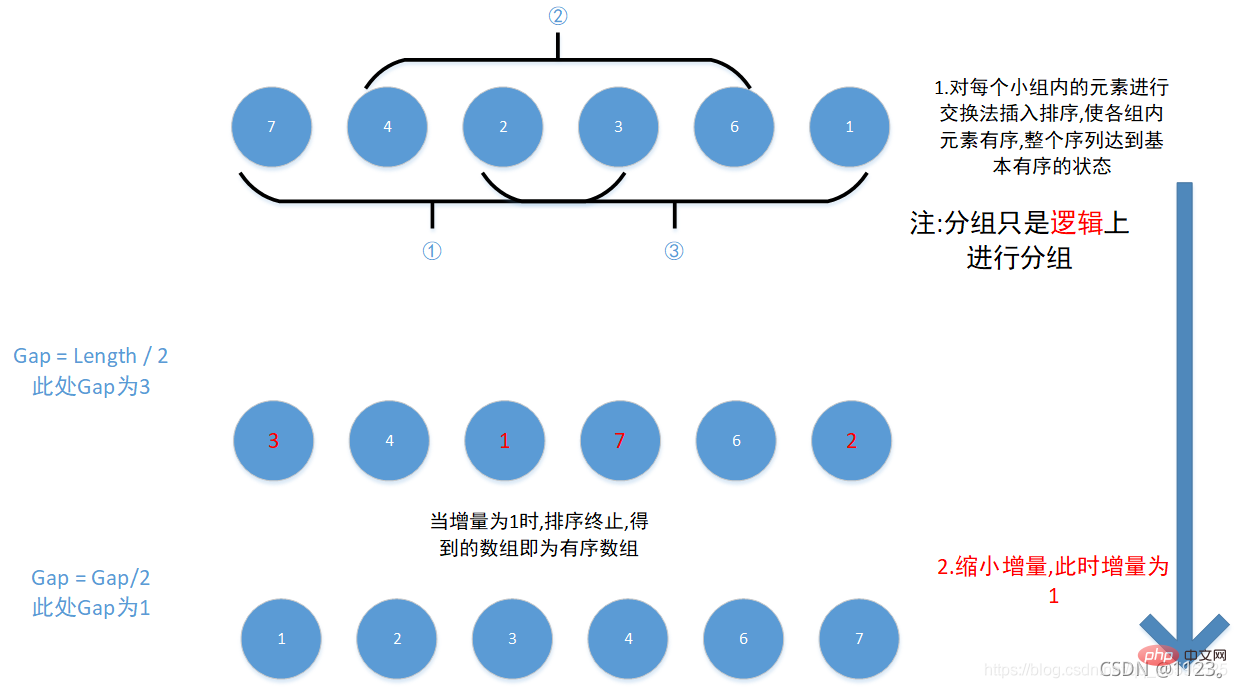
1. 思路图解

2. 代码实现

public static void shellSort(int[] arr){ //交换法
        int tmp = 0;
        for(int gap = arr.length / 2 ; gap > 0 ; gap /= 2){
            for(int i = gap ; i < arr.length ; i++){ //先遍历所有数组
                for(int j  = i - gap ; j >= 0 ; j -= gap){//开启插入排序
                    if(arr[ j ] > arr[ gap + j ]){ //可以根据升降序修改大于或小于
                        tmp = arr[gap + j];
                        arr[j+gap] = arr[j];
                        arr[j] = tmp;
                    }
                }
            }
            System.out.println(gap);
            System.out.println(Arrays.toString(arr));
        }
    }
12345678910111213141516

这里最难理解的应该是第三个for循环,j = i - gap, 表示小组内的第一个元素,即j=0,

当小组内的第一个元素大于第二个元素时(由于是逻辑上的分类,第二个元素的索引应当是第一个元素的所有值+增量gap) , 交换两者,反之j-=gap,继续比较或跳出循环 ,

如此往复将所有小组都遍历完之后 , 缩小增量(即gap/=2) , 然后继续上述步骤, 直到增量gap为1时, 序列排序结束

3. 时间复杂度

希尔排序的时间复杂度取决于增量序列的函数 , 需要具体问题具体分析,并不是一个确定的值,这也是第四点需要讨论的问题

4. 关于增量的选择

上述我们在做排序的时候增量缩减选用的时gap/=2的模型, 这并不是最优的选择 , 关于增量的选取 , 属于数学界尚未解决的一个问题

但是可以确定的是, 通过大量的实验证明 ,当n->无穷大

Puisque nous opérons sur le tableau, nous devons également obtenir le

ordered set L'index du dernier élément est utilisé comme curseur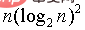

Lorsque le curseur ne franchit pas la limite et que la valeur à insérer est inférieure à la position indiquée par le curseur (4 dans l'image ci-dessus), on recule l'élément 4, Le curseur avance et continue de vérifier si les autres éléments de l'ensemble sont plus petits que l'élément à insérer jusqu'à ce que le curseur franchisse la limite dans l'image ci-dessus, puisqu'il y en a. un seul 4 dans l'ensemble, le curseur avance et franchit la limite, donc la boucle se termine<strong> </strong>2 Implémentation du code

public static void shellSort02(int[] arr){ //移位法
        for(int gap = arr.length/2 ; gap > 0 ; gap /= 2){ //分组
            for(int i = gap ; i < arr.length ; i++){ //遍历
                int valIndex = i;
                int val = arr[valIndex];
                if(val < arr[valIndex-gap]){ //插入的值小于组内另一个值
                   while(valIndex - gap >=0 && val < arr[valIndex-gap]){ //开始插排
                       // 插入
                       arr[valIndex] = arr[valIndex-gap];
                       valIndex -= gap; //让valIndex = valIndex-gap (游标前移)
                   }
                }
                arr[valIndex] = val;
            }
        }
    }
12345678910111213141516

3 Tests de performances et complexité spatio-temporelle

Cela prend en fait. 1 minute et 4 secondes pour exécuter 800 000 données (valeur non précise, chaque machine peut être différente)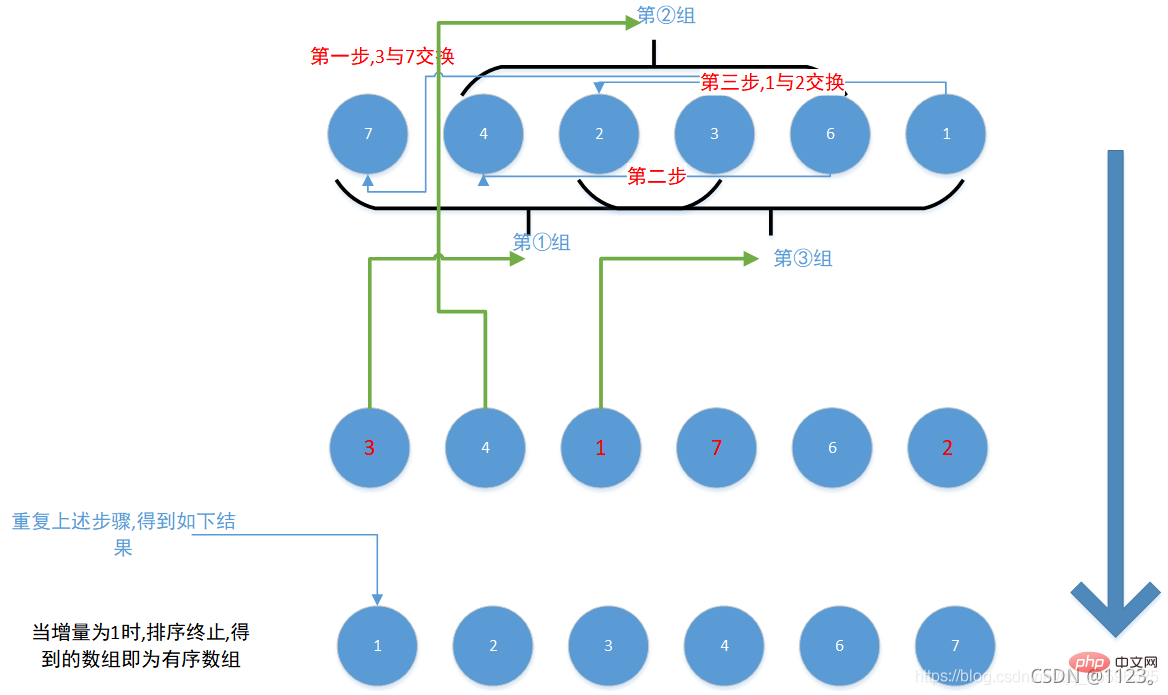

L'insertion directe et le tri des enregistrements sont moindres, les mots-clés L'efficacité est plus élevée lorsqu'elle est essentiellement ordonnée

Complexité temporelle :Nombre de comparaisons de mots clés : KCN=(n^2)/2 Nombre total de mouvements : RMN= ( n^2)/2

La complexité temporelle est donc d'environ O(N^2)2. Tri en colline (méthode d'échange)

1. Illustration des idées

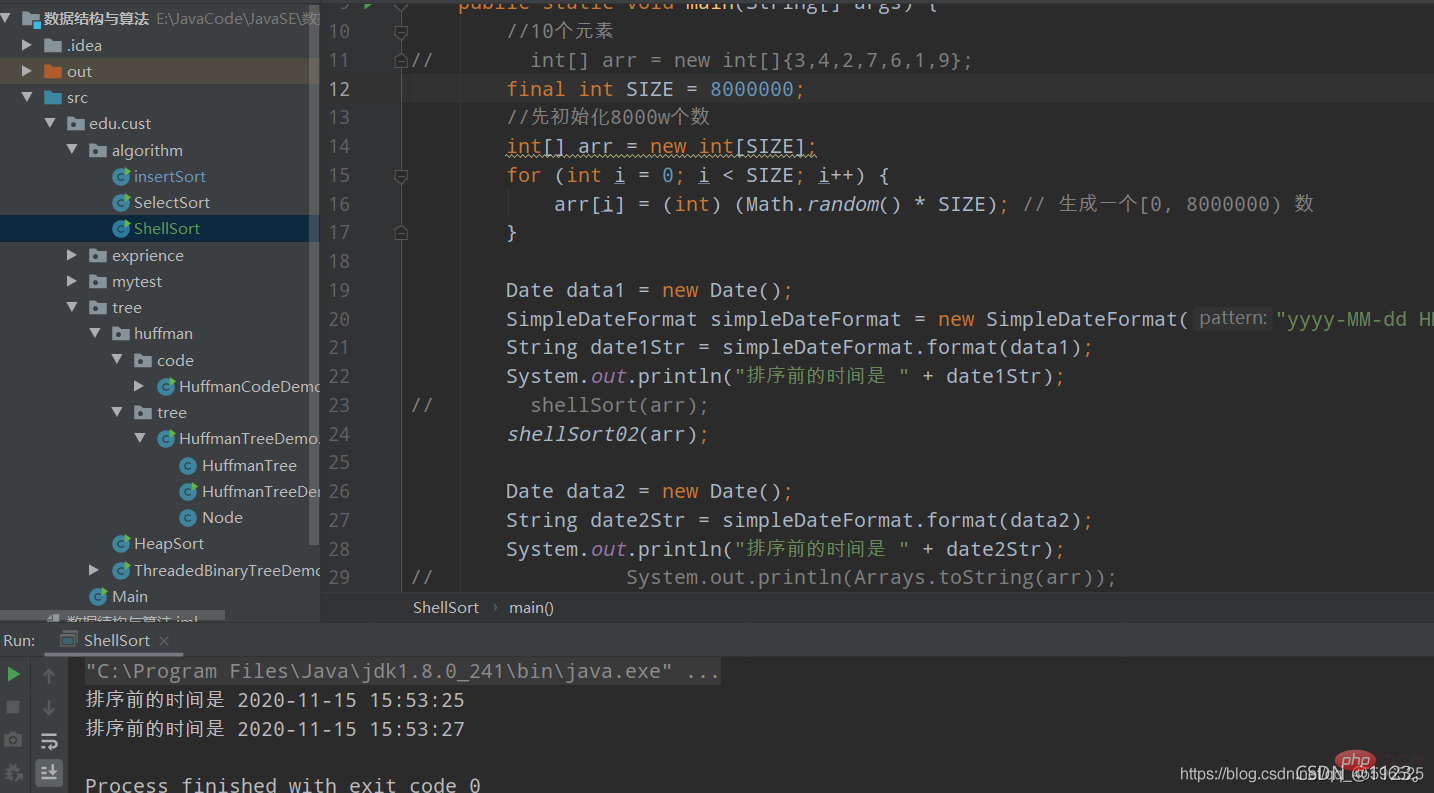2. Implémentation du code

rrreee

La chose la plus difficile à comprendre ici est probablement la troisième boucle for, j = i - gap, qui représente le premier élément du groupe, c'est-à-dire j=0,

Lorsque le premier élément du groupe est supérieur au deuxième élément (
En raison de la classification logique, l'index du deuxième élément doit être toutes les valeurs du premier élément + l'écart incrémentiel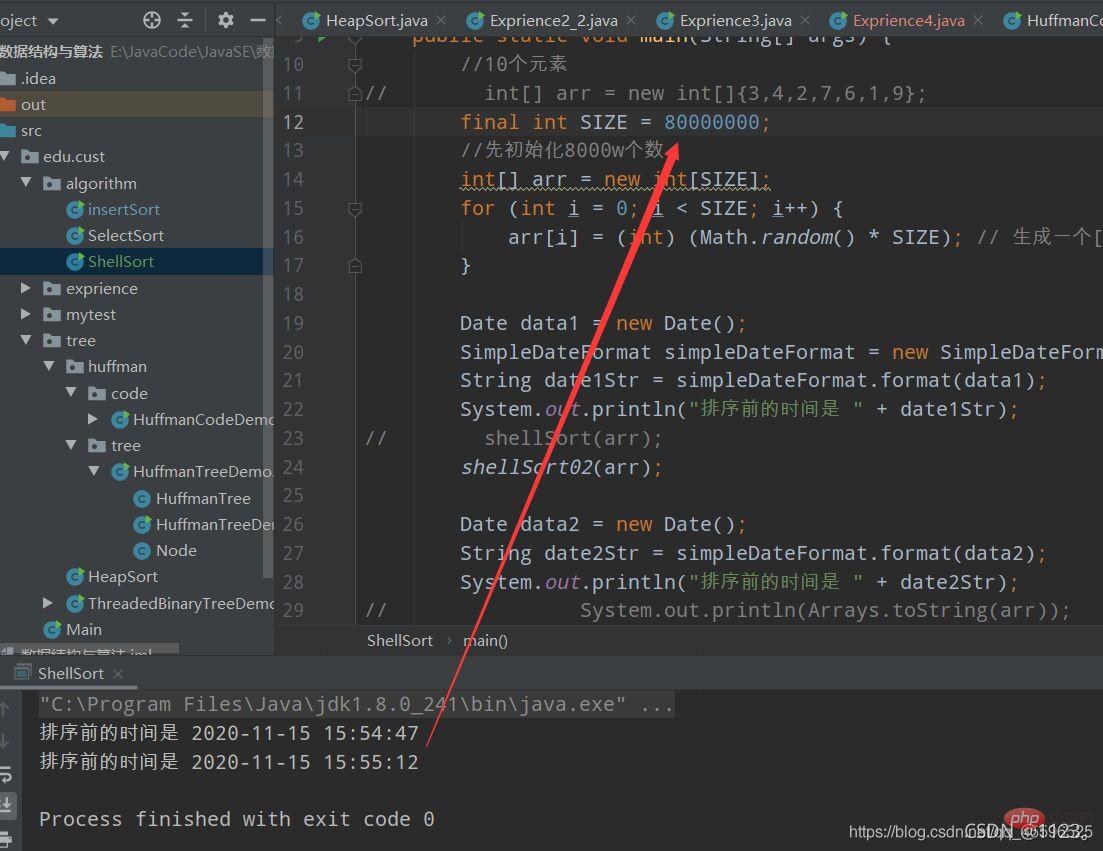), échangez les deux, Sinon j-=gap, continuez pour comparer ou sortir de la boucle,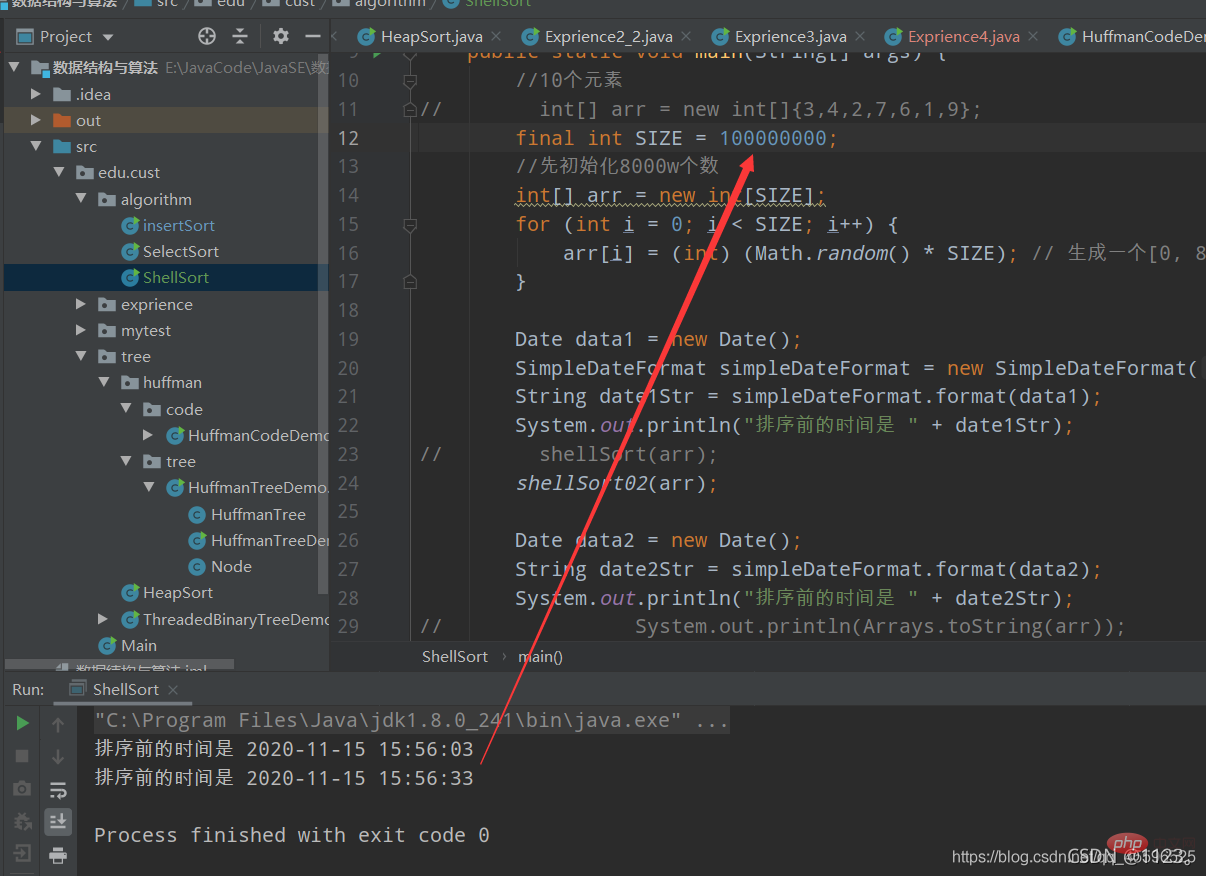
Après avoir parcouru tous les groupes de cette manière, réduisez l'incrément (c'est-à-dire gap/=2), puis continuez les étapes ci-dessus jusqu'à ce que l'écart incrémentiel soit de 1 , et le tri séquentiel se termine

🎜3. Complexité temporelle🎜🎜La complexité temporelle du tri Hill dépend de🎜la fonction de la séquence incrémentielle🎜, qui nécessite une analyse spécifique de problèmes spécifiques et n'est pas la même valeur déterminée, c'est aussi la quatrième point qui doit être discuté🎜🎜4. Concernant le choix de l'incrément🎜🎜Lorsque nous avons fait le tri ci-dessus🎜réduction incrémentale🎜lorsque nous avons choisi le modèle gap/=2, ce n'est pas le choix optimal. . La sélection des incréments est un problème non résolu dans la communauté mathématique🎜🎜Mais ce qui est sûr c'est qu'à travers un grand nombre d'expériences, il a été prouvé que lorsque n->infini code>, la complexité temporelle peut se réduire à : 🎜🎜🎜🎜🎜Dans le point suivant, 🎜méthode shift🎜, nous avons également fait plusieurs expériences, et nous pouvons être sûrs que pour une certaine échelle (comme 800w~100 millions) En termes de calcul, 🎜Le tri Hill est beaucoup plus rapide que le tri par tas🎜, du moins sur mon ordinateur 🎜🎜3. Tri Hill (méthode Shift)🎜🎜La méthode d'échange est beaucoup plus lente que la méthode Shift, donc la 🎜méthode Shift🎜 est plus couramment utilisée. , et la méthode de décalage ressemble plus au tri par insertion 🎜🎜1. L'idée 🎜🎜L'idée est en fait une combinaison des deux méthodes de tri ci-dessus, regroupant 🎜 en groupes🎜 Combinée aux avantages de 🎜insertion🎜, l'efficacité est very high🎜🎜 incarne l'idée de 🎜diviser pour régner🎜, découpant une séquence plus grande en plusieurs séquences plus petites🎜🎜🎜🎜🎜2 Implémentation du code🎜rrreee🎜3.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!