Utiliser Python pour implémenter la détection du sol par nuages ​​de points

1. Système de coordonnées de vision par ordinateur

Avant de commencer, il est important de comprendre le système de coordonnées traditionnel en vision par ordinateur. Viennent ensuite Open3D et le capteur Microsoft Kinect. En vision par ordinateur, les images sont représentées par un système de coordonnées 2D distinct, où l'axe des x pointe de gauche à droite et l'axe des y pointe de haut en bas. Pour une caméra, l'origine du système de coordonnées 3D se trouve au foyer de la caméra, l'axe x pointant vers la droite, l'axe y pointant vers le bas et l'axe z pointant vers l'avant.

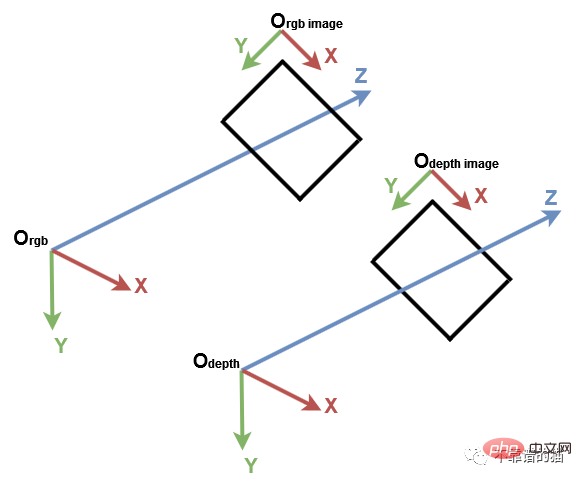
Système de coordonnées de vision par ordinateur

Nous importons d'abord la bibliothèque Python requise :

import numpy as np
import open3d as o3d

Pour une meilleure compréhension, importons des nuages ​​de points à partir de fichiers PLY, créons des systèmes de coordonnées 3D par défaut à l'aide d'Open3D et affichons-les :

# Read point cloud:
pcd = o3d.io.read_point_cloud("data/depth_2_pcd.ply")
# Create a 3D coordinate system:
origin = o3d.geometry.TriangleMesh.create_coordinate_frame(size=0.5)
# geometries to draw:
geometries = [pcd, origin]
# Visualize:
o3d.visualization.draw_geometries(geometries)

Nuage de points affiché avec l'origine du système de coordonnées

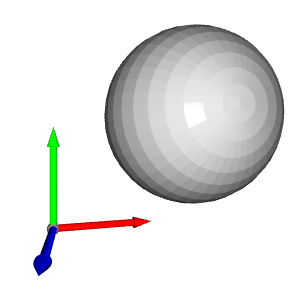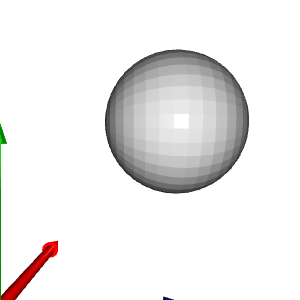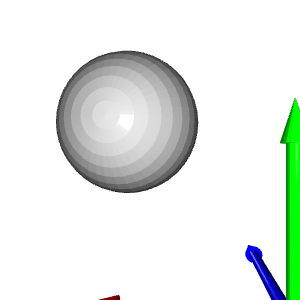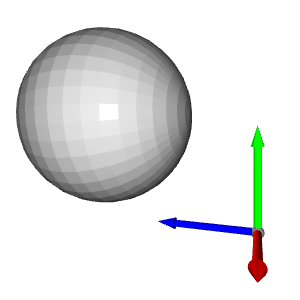
La flèche bleue est l'axe Z, la flèche rouge est l'axe X et la flèche verte est l'axe Y. Vous pouvez voir que le nuage de points est représenté dans le même système de coordonnées que le système de coordonnées Open3D. Maintenant, récupérons les points avec les valeurs minimales et maximales de chaque axe :

# Get max and min points of each axis x, y and z:
x_max = max(pcd.points, key=lambda x: x[0])
y_max = max(pcd.points, key=lambda x: x[1])
z_max = max(pcd.points, key=lambda x: x[2])
x_min = min(pcd.points, key=lambda x: x[0])
y_min = min(pcd.points, key=lambda x: x[1])
z_min = min(pcd.points, key=lambda x: x[2])

Nous pouvons les imprimer, mais pour une meilleure visualisation, nous créons une sphère à chaque emplacement de point. Par défaut, Open3D crée des géométries 3D à la position d'origine :

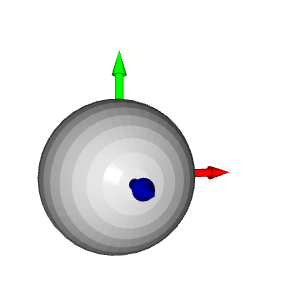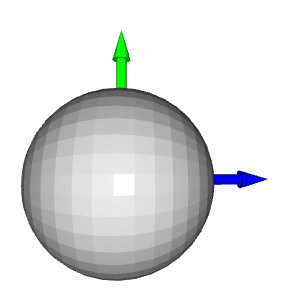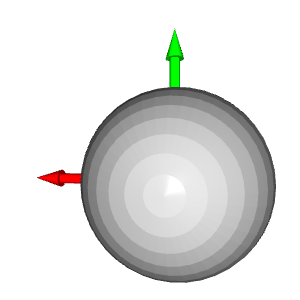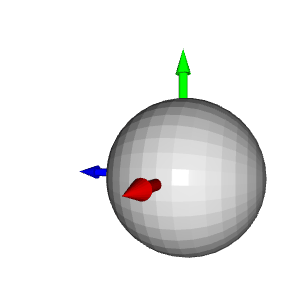
Pour déplacer la sphère vers une position donnée, une transformation de translation est nécessaire. Dans l'exemple ci-dessous, la sphère est traduite par le vecteur [1,1,1] :

Reprenons notre exemple et attribuons une couleur à chaque sphère. Pour chaque position, nous créons une sphère et la traduisons vers cette position. Ensuite, nous attribuons la bonne couleur et enfin nous l'ajoutons à l'affichage.

# Colors:
RED = [1., 0., 0.]
GREEN = [0., 1., 0.]
BLUE = [0., 0., 1.]
YELLOW = [1., 1., 0.]
MAGENTA = [1., 0., 1.]
CYAN = [0., 1., 1.]


positions = [x_max, y_max, z_max, x_min, y_min, z_min]
colors = [RED, GREEN, BLUE, MAGENTA, YELLOW, CYAN]
for i in range(len(positions)):
 # Create a sphere mesh:
 sphere = o3d.geometry.TriangleMesh.create_sphere(radius=0.05)
 # move to the point position:
 sphere.translate(np.asarray(positions[i]))
 # add color:
 sphere.paint_uniform_color(np.asarray(colors[i]))
 # compute normals for vertices or faces:
 sphere.compute_vertex_normals()
 # add to geometry list to display later:
 geometries.append(sphere)


# Display:
o3d.visualization.draw_geometries(geometries)

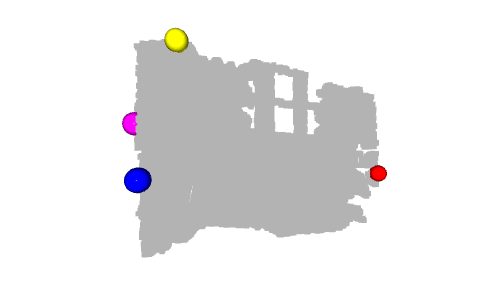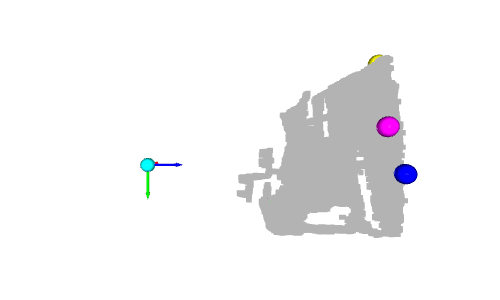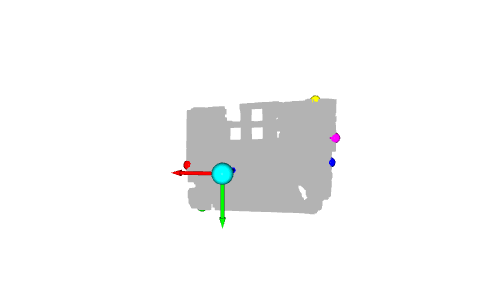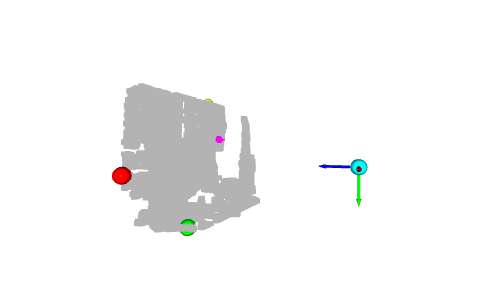
En fait, l'axe y représente la hauteur du point : dans le monde réel, la boule la plus haute est la boule jaune et la boule la plus basse est la boule verte. Cependant, comme l’axe des y est orienté vers le bas, la sphère jaune a la plus petite valeur et la sphère verte a la plus grande valeur.

Une autre sphère intéressante est la sphère cyan à l'origine. Comme nous l'avons mentionné dans le tutoriel précédent, les pixels avec une valeur de profondeur de 0 sont des points de bruit, donc le point à l'origine est le point calculé à partir de ces pixels de bruit (quand z=0, alors x=0 et y= 0).

2. Détection au sol

Maintenant que nous avons montré quelques points importants, qu'en est-il de la détection au sol ? Dans l'exemple précédent, la sphère verte est située au sol. Pour être précis, son centre correspond au point le plus haut de l'axe y qui est un point au sol. Supposons que pour la détection au sol, nous changeons la couleur de tous les points avec y_max en vert

Si vous affichez le nuage de points, vous remarquerez que tous les points au sol ne sont pas verts. En fait, un seul point, correspondant au centre de la sphère verte précédente, est vert. Cela est dû à la précision et au bruit de la caméra de profondeur.

Pour surmonter cette limitation, nous devons ajouter un seuil afin que les points avec des coordonnées y de [y_max-threshold, y_max] soient considérés comme des points au sol. Pour ce faire, après avoir obtenu y_max, nous vérifions si la coordonnée y de chaque point est dans l'intervalle, puis définissons sa couleur sur vert. Enfin, les attributs de couleur du nuage de points sont mis à jour et les résultats sont affichés.

# Define a threshold:
THRESHOLD = 0.075


# Get the max value along the y-axis:
y_max = max(pcd.points, key=lambda x: x[1])[1]


# Get the original points color to be updated:
pcd_colors = np.asarray(pcd.colors)


# Number of points:
n_points = pcd_colors.shape[0]


# update color:
for i in range(n_points):
# if the current point is aground point:
if pcd.points[i][1] >= y_max - THRESHOLD:
pcd_colors[i] = GREEN# color it green


pcd.colors = o3d.utility.Vector3dVector(pcd_colors)


# Display:
o3d.visualization.draw_geometries([pcd, origin])

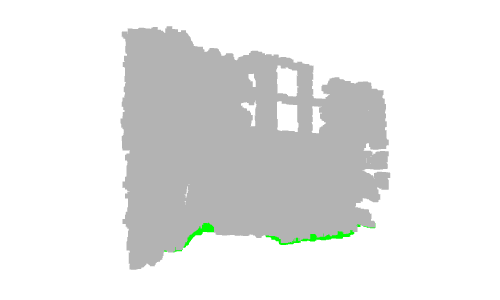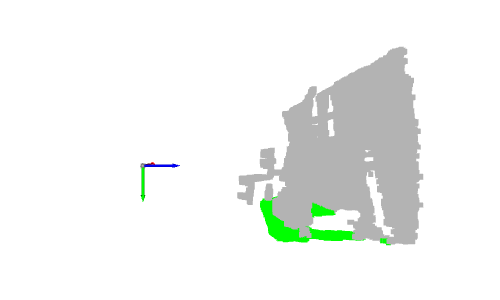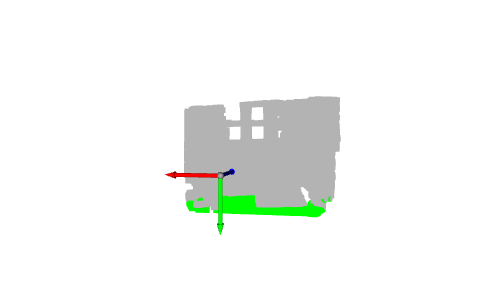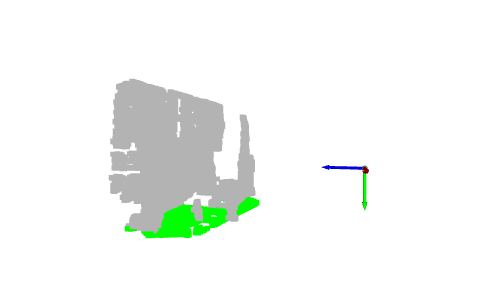
Dans ce cas, nous colorerons uniquement les points représentant le sol en vert. Dans les applications du monde réel, le sol est extrait pour définir des zones accessibles à pied, telles que des robots ou des systèmes malvoyants, ou pour y placer des objets, tels que des systèmes de décoration intérieure. Il peut également être supprimé, de sorte que les points restants puissent être segmentés ou classés, comme dans les systèmes de compréhension de scène et de détection d'objets.

3. Nuage de points organisé

Nous savons qu'un nuage de points est défini comme un ensemble de points 3D. Un ensemble est une structure non ordonnée, c'est pourquoi le nuage de points représenté par l'ensemble est appelé nuage de points non organisé. Semblable à une matrice RVB, un nuage de points organisé est une matrice 2D avec 3 canaux représentant les coordonnées x, y et z des points. La structure matricielle fournit la relation entre les points adjacents, réduisant ainsi la complexité temporelle de certains algorithmes, tels que l'algorithme du voisin le plus proche.

Par exemple, nous rédigeons un document de recherche et nous souhaitons montrer les résultats de notre algorithme de détection sous forme graphique. Nous pouvons soit prendre une capture d'écran du nuage de points, soit afficher les résultats sur une image de profondeur, comme indiqué ci-dessous. À mon avis, la deuxième option est la meilleure. Dans ce cas, un nuage de points organisé est nécessaire pour enregistrer les positions des pixels de profondeur.

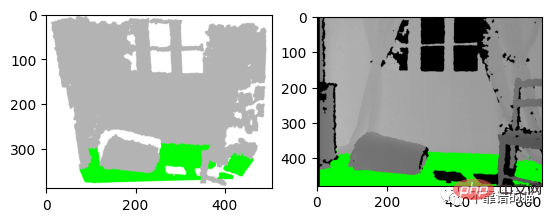
左：3D 可视化的屏幕截图 右：深度图像的结果

让我们从之前的深度图像创建一个有组织的点云。我们首先导入相机参数。我们还导入深度图像并将其转换为3通道灰度图像，以便我们可以将地面像素设置为绿色：

import imageio.v3 as iio
import numpy as np
import matplotlib.pyplot as plt


# Camera parameters:
FX_DEPTH = 5.8262448167737955e+02
FY_DEPTH = 5.8269103270988637e+02
CX_DEPTH = 3.1304475870804731e+02
CY_DEPTH = 2.3844389626620386e+02


# Read depth image:
depth_image = iio.imread('../data/depth_2.png')
# Compute the grayscale image:
depth_grayscale = np.array(256 * depth_image / 0x0fff, dtype=np.uint8)
# Convert a grayscale image to a 3-channel image:
depth_grayscale = np.stack((depth_grayscale,) * 3, axis=-1)

要计算一个有组织的点云，我们使用与上一篇教程相同的方法（Python：基于 RGB-D 图像的点云计算）。我们没有将深度图像扁平化，而是将jj和ii重塑为与深度图像相同的形状，如下所示:

# get depth image resolution:
height, width = depth_image.shape
# compute indices and reshape it to have the same shape as the depth image:
jj = np.tile(range(width), height).reshape((height, width))
ii = np.repeat(range(height), width).reshape((height, width))
# Compute constants:
xx = (jj - CX_DEPTH) / FX_DEPTH
yy = (ii - CY_DEPTH) / FY_DEPTH
# compute organised point cloud:
organized_pcd = np.dstack((xx * depth_image, yy * depth_image, depth_image))

如果你打印出创建的点云的形状，你可以看到它是一个有3个通道的矩阵(480,640,3)。如果你觉得这个代码很难理解，请回到之前的教程（Python：基于 RGB-D 图像的点云计算）。

类似地，我们像上面那样检测地面，但不是更新点的颜色并显示点云，而是更新灰度图像的像素并显示它:

# Ground_detection:
THRESHOLD = 0.075 * 1000# Define a threshold
y_max = max(organized_pcd.reshape((height * width, 3)), key=lambda x: x[1])[
1]# Get the max value along the y-axis


# Set the ground pixels to green:
for i in range(height):
for j in range(width):
if organized_pcd[i][j][1] >= y_max - THRESHOLD:
depth_grayscale[i][j] = [0, 255, 0]# Update the depth image


# Display depth_grayscale:
plt.imshow(depth_grayscale)
plt.show()

4.结论

在本教程中，为了熟悉点云，我们引入了默认坐标系统，并实现了一个简单的地面检测算法。事实上，地面检测在某些应用(如导航)中是一项重要的任务，文献中已经提出了几种算法。实现算法简单;它认为最低点是地面。然而，它的限制是，深度相机必须与地面平行，这是大多数现实应用的情况不是这样的。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!