Comment tracer une coque convexe en Python ?

ConvexHull

ConvexHull est une classe spatiale. Sa fonction principale est de trouver les bords d'un ensemble de points et de créer une coque convexe. Le paramètre d'initialisation nécessaire est un ensemble de points, le format de l'ensemble de points est un tableau de n×m dimensions, n est le nombre de points dans l'ensemble de points et m est la dimension du point.

from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
import numpy as np

pts = np.random.rand(30, 2)
hull = ConvexHull(pts)
plt.plot(pts[:,0], pts[:,1], 'o')
for i in hull.simplices:
    plt.plot(pts[i, 0], pts[i, 1], 'k-')

plt.show()

où simplex est le numéro de série du point d'index. L'effet après le dessin est le suivant

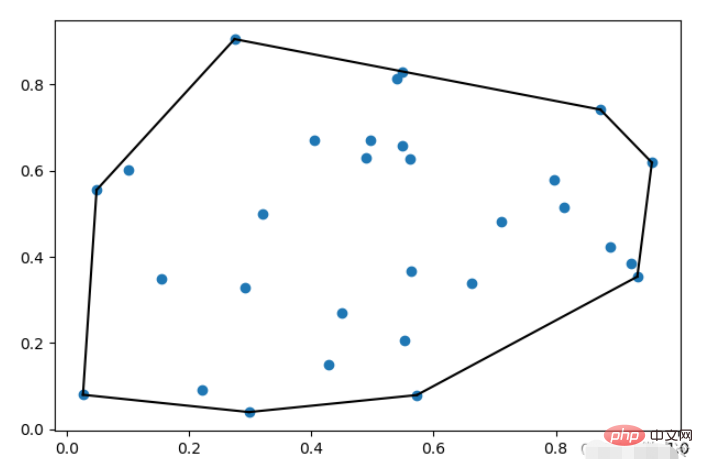
ConvexHull a deux paramètres facultatifs. Incrémental est un paramètre booléen. Lorsqu'il est vrai, de nouveaux points peuvent être ajoutés. .

Les paramètres spécifiques de qhull_options peuvent être visualisés dans qhull Seul QG sera démontré ci-dessous.

QG

QGn signifie que le nième point est considéré comme le point d'observation. Après avoir divisé le point défini par l'enveloppe convexe, si les sommets sont connectés et utilisés comme mur, alors les points visibles par le point d'observation sont. marqué comme bon, l'effet est comme indiqué ci-dessous

pts = np.random.rand(1000, 2)
# 添加一个观察点
pts = np.vstack([pts, np.array([[2,0.5]])])
hull = ConvexHull(pts, qhull_options='QG1000')
plt.plot(pts[:,0], pts[:,1], '.')
for i in hull.simplices:
    plt.plot(pts[i, 0], pts[i, 1], 'k-')

for i in hull.simplices[hull.good]:
    plt.plot(pts[i, 0],pts[i, 1], lw=5)

plt.show()

L'effet est comme le montre l'image

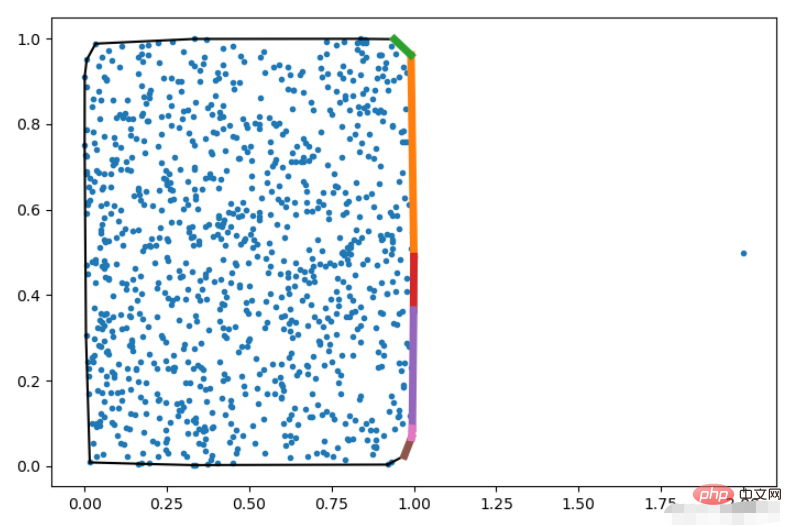
Boîtier tridimensionnel

La coque convexe dans le boîtier bidimensionnel est évidemment une figure fermée composée de lignes, et la coque convexe dans le cas tridimensionnel devrait naturellement être une géométrie tridimensionnelle. Étendu à n'importe quelle dimension, l'enveloppe convexe est en fait un simplexe. Les simplexes de ConvexHull sont les points qui composent le simplexe et sont indexés dans l'ensemble d'origine. L'exemple est le suivant

pts = np.random.rand(30, 3)
hull = ConvexHull(pts)
ax = plt.subplot(projection='3d')
ax.scatter(pts[:,0], pts[:,1], pts[:,2])
for i in hull.simplices:
    ax.plot_trisurf(pts[i, 0], pts[i, 1], pts[i,2], alpha=0.5)

plt.show()

Le paramètre alpha est utilisé pour ajuster la transparence de la surface triangulaire, de sorte que les points à l'intérieur de la coque convexe puissent être vus à travers la coque convexe.

L'effet est le suivant

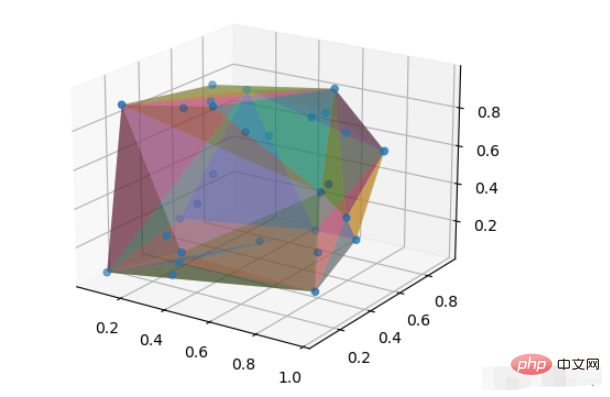
Attribut ConvexHull

Le concept de simplex a déjà été introduit, c'est-à-dire que la figure composée de la coque convexe est un simplex. Dans le cas bidimensionnel, l'enveloppe convexe est entourée de segments de ligne ; dans le cas tridimensionnel, l'enveloppe convexe est entourée de plans, elle peut être exprimée comme un simplex qui constitue l'enveloppe convexe, entourée. par les hypersurfaces. Puisque le concept d’hypersurface n’a pas de frontières, la surface de coque convexe avec ses sommets et ses arêtes est appelée ci-après hypersurface simplexe.

Les attributs couramment utilisés dans la classe ConvexHull sont les suivants

• ensemble de points de points entourés d'une coque convexe

• index des sommets du sommet simplex dans l'ensemble de points

• simplices simplex hypersurface

• ne super surface des voisins Indices des hypersurfaces adjacentes

• équations Paramètres des équations d'hypersurface

Des exemples d'équations d'hypersurface dans le cas tridimensionnel sont les suivants, c'est-à-dire que chaque hypersurface a 4 paramètres

>>> hull.equations
array([[-0.5509472 ,  0.72386104, -0.41530999, -0.36369123],
       [-0.26155355,  0.16210178, -0.95147925,  0.02022163],
       [-0.99132368, -0.0460725 ,  0.12310441,  0.045523  ],
       [-0.98526526, -0.07170442,  0.15527666,  0.04749854],
       [-0.15900968, -0.98529789, -0.06248198,  0.13294496],
   # .......

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!