Exemple d'analyse d'arbre de recherche binaire Java

Concept

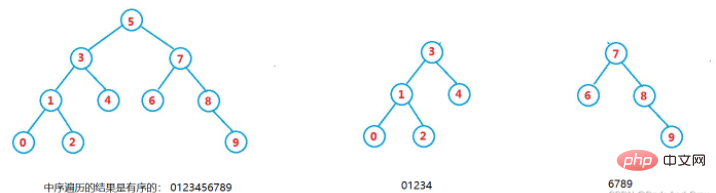
L'arbre de recherche binaire est également appelé arbre de tri binaire. Il s'agit soit d'un arbre vide, soit d'un arbre binaire avec les propriétés suivantes :
1. Si son sous-arbre de gauche n'est pas vide, alors Les valeurs. de tous les nœuds du sous-arbre de gauche sont inférieurs à la valeur du nœud racine.
2. Si son sous-arbre droit n'est pas vide, alors les valeurs de tous les nœuds du sous-arbre droit sont supérieures à la valeur du nœud racine.
3. Ses sous-arbres gauche et droit sont également respectivement des arbres de recherche binaires

Pratique directe

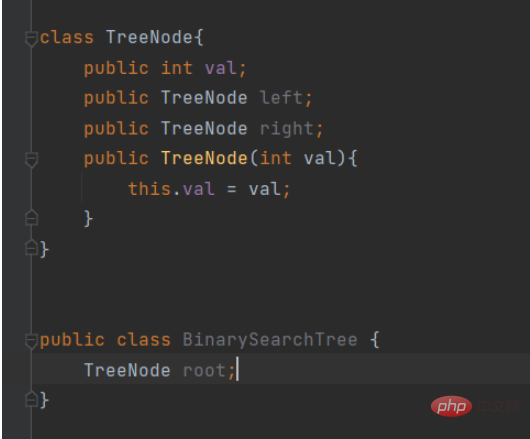
Travail de préparation : définir une classe de nœuds d'arbre et une classe d'arbre de recherche binaire.

Recherchez la fonction de recherche d'un arbre binaire

Supposons que nous ayons construit un tel arbre binaire, comme indiqué ci-dessous

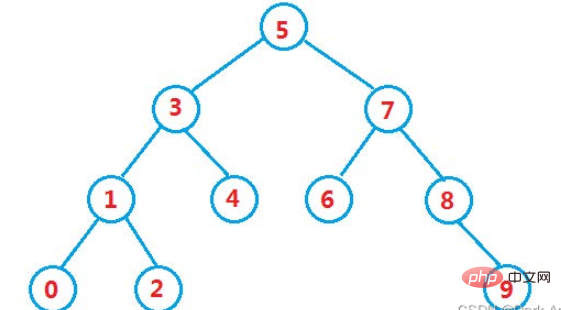
La première question à laquelle nous voulons réfléchir est de savoir comment savoir si une certaine valeur est dans l'arbre binaire ?

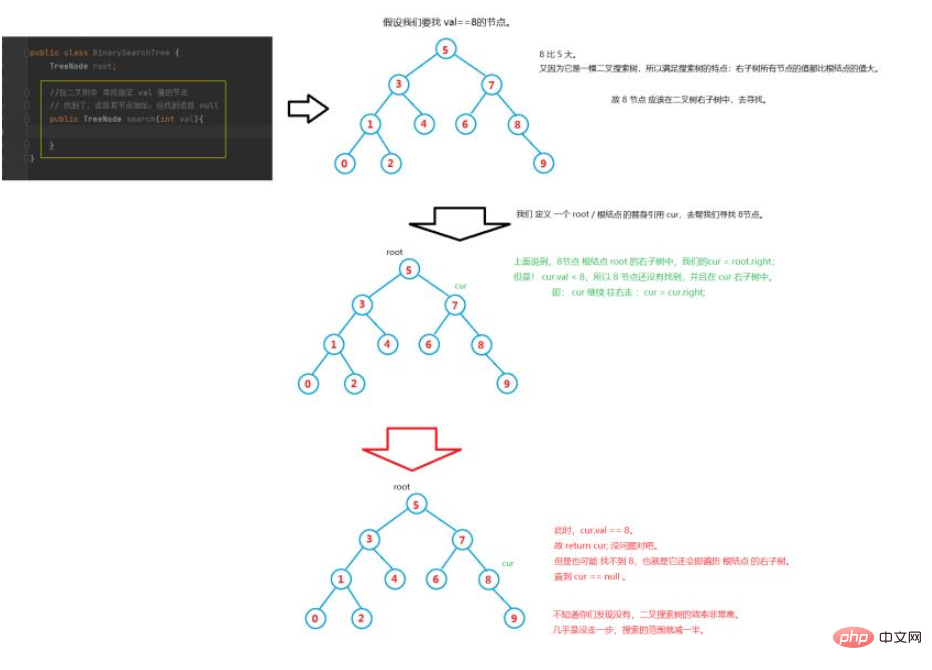
Sur la base de la logique ci-dessus, améliorons la méthode de recherche.

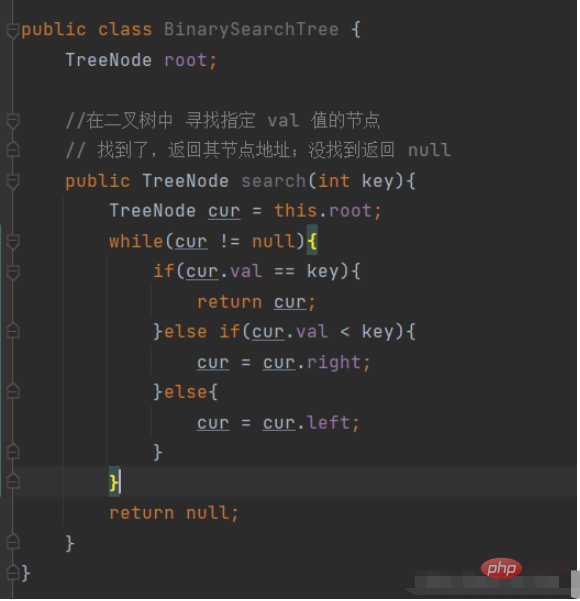
Recherchez l'opération d'insertion de l'arbre binaire

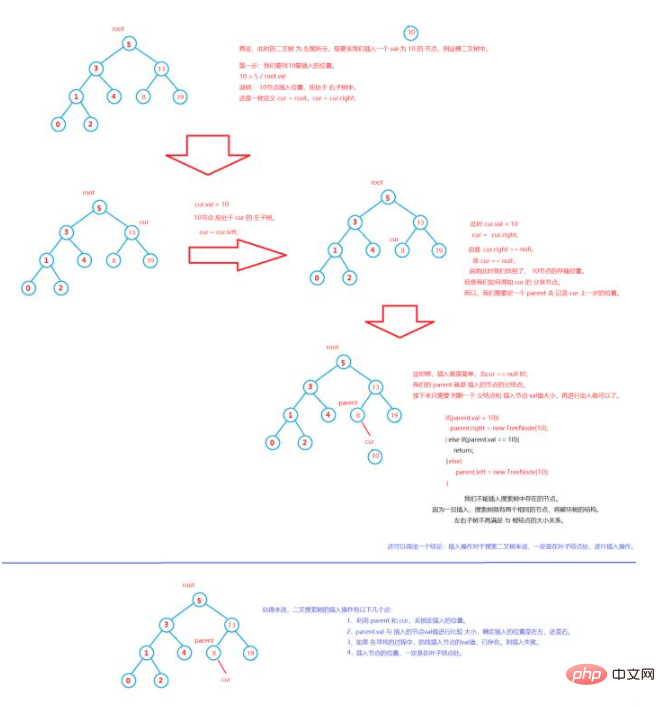
Sur la base de la logique ci-dessus, écrivons un code pour insérer un nœud.

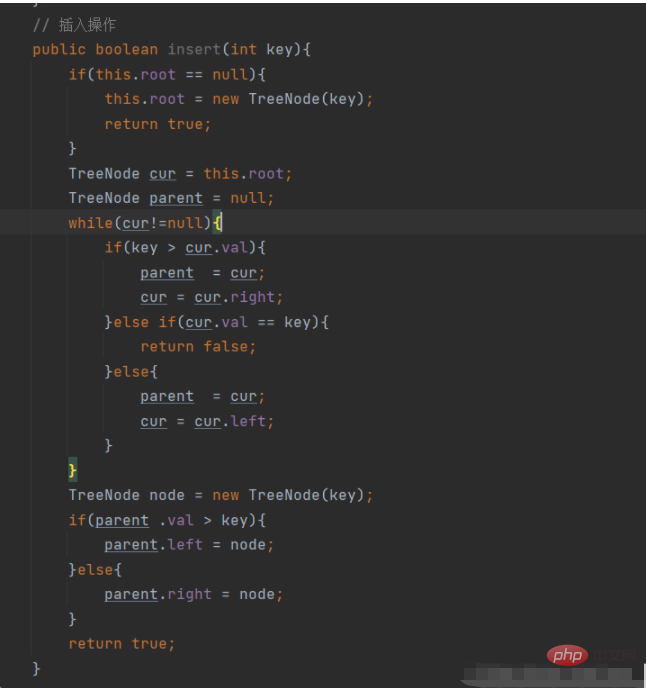
Rechercher l'opération de suppression de nœuds dans un arbre binaire - difficulté

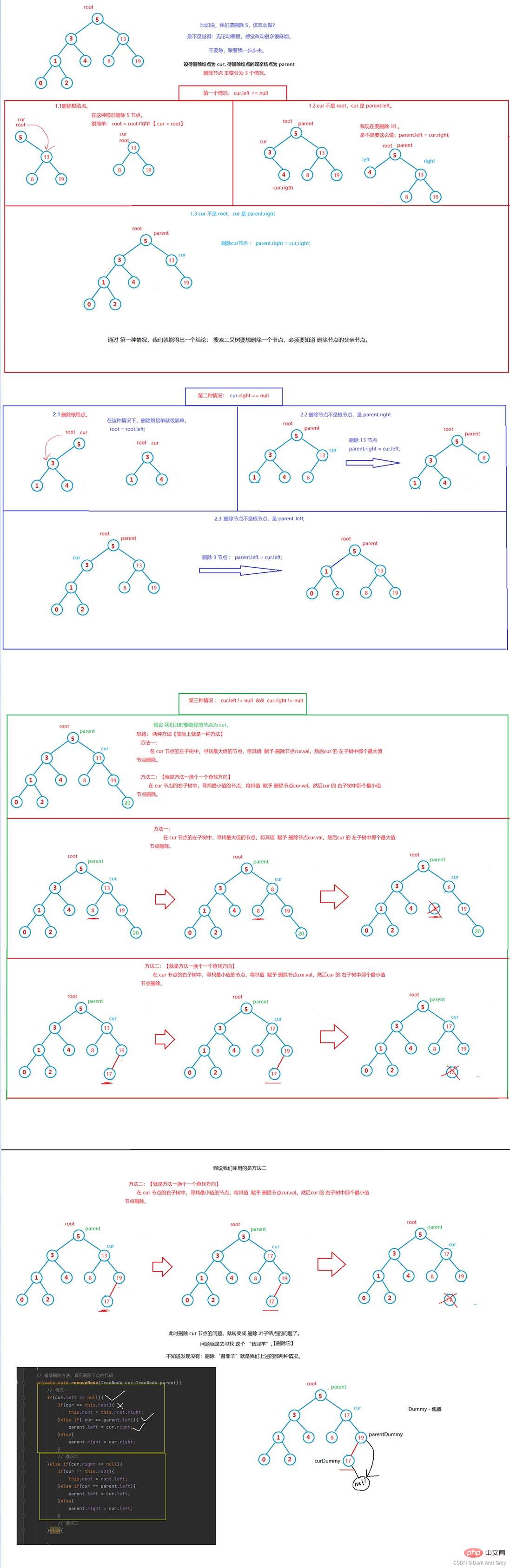
Analysons encore : comment curDummy et parentDummy trouvent le "bouc émissaire".

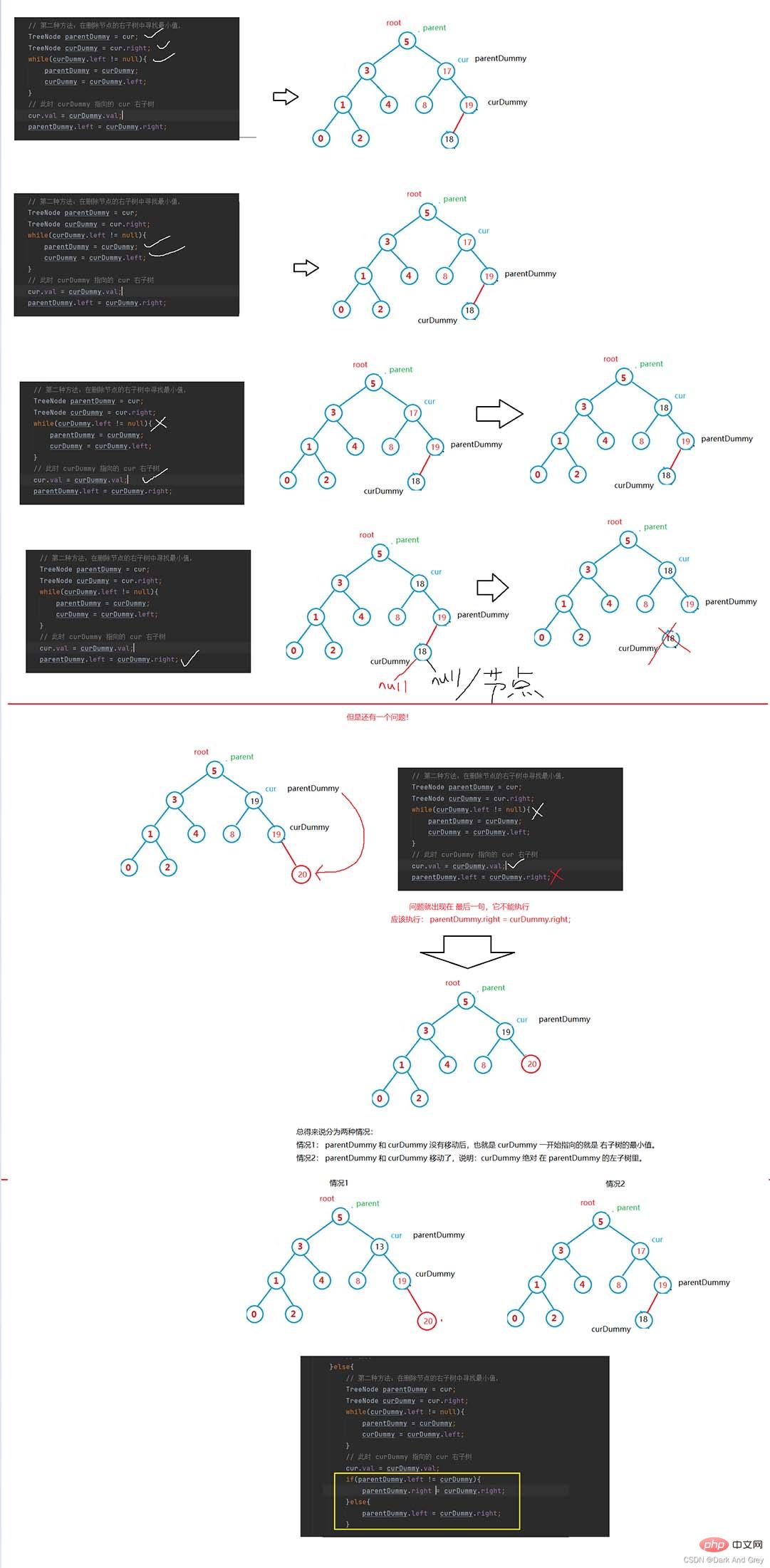
Programme général - Simuler la mise en œuvre d'un arbre de recherche binaire

class TreeNode{
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val){
        this.val = val;
    }
}


public class BinarySearchTree {
    TreeNode root;

    //在二叉树中 寻找指定 val 值的节点
    // 找到了，返回其节点地址；没找到返回 null
    public TreeNode search(int key){
        TreeNode cur = this.root;
        while(cur != null){
            if(cur.val == key){
                return cur;
            }else if(cur.val < key){
                cur = cur.right;
            }else{
                cur = cur.left;
            }
        }
        return null;
    }
    // 插入操作
    public boolean insert(int key){
        if(this.root == null){
            this.root = new TreeNode(key);
            return true;
        }
        TreeNode cur = this.root;
        TreeNode parent = null;
        while(cur!=null){
            if(key > cur.val){
                parent  = cur;
                cur = cur.right;
            }else if(cur.val == key){
                return false;
            }else{
                parent  = cur;
                cur = cur.left;
            }
        }
        TreeNode node = new TreeNode(key);
        if(parent .val > key){
            parent.left = node;
        }else{
            parent.right = node;
        }
        return true;
    }
    // 删除操作
    public void remove(int key){
        TreeNode cur = root;
        TreeNode parent = null;
        // 寻找 删除节点位置。
        while(cur!=null){
            if(cur.val == key){
                removeNode(cur,parent);// 真正删除节点的代码
                break;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else{
                parent = cur;
                cur = cur.left;
            }
        }
    }
    // 辅助删除方法：真正删除节点的代码
    private void removeNode(TreeNode cur,TreeNode parent){
        // 情况一
        if(cur.left == null){
            if(cur == this.root){
                this.root = this.root.right;
            }else if( cur == parent.left){
                parent.left = cur.right;
            }else{
                parent.right = cur.right;
            }
            // 情况二
        }else if(cur.right == null){
            if(cur == this.root){
                this.root = root.left;
            }else if(cur == parent.left){
                parent.left = cur.left;
            }else{
                parent.right = cur.left;
            }
            // 情况三
        }else{
            // 第二种方法：在删除节点的右子树中寻找最小值，
            TreeNode parentDummy = cur;
            TreeNode curDummy = cur.right;
            while(curDummy.left != null){
                parentDummy = curDummy;
                curDummy = curDummy.left;
            }
            // 此时 curDummy 指向的 cur 右子树
            cur.val = curDummy.val;
            if(parentDummy.left != curDummy){
                parentDummy.right = curDummy.right;
            }else{
                parentDummy.left = curDummy.right;
            }

        }
    }
   // 中序遍历
    public void inorder(TreeNode root){
        if(root == null){
            return;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }

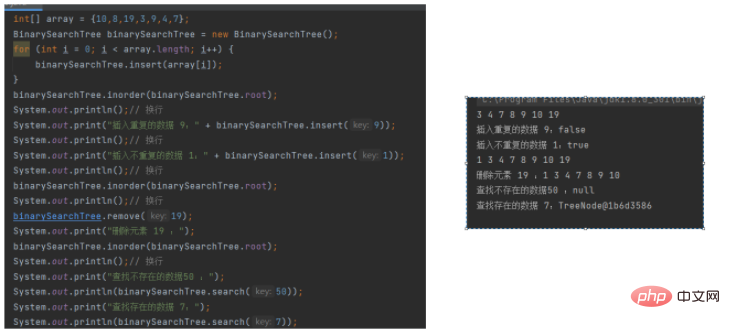
    public static void main(String[] args) {
        int[] array = {10,8,19,3,9,4,7};
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        for (int i = 0; i < array.length; i++) {
            binarySearchTree.insert(array[i]);
        }
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        System.out.print("插入重复的数据 9：" + binarySearchTree.insert(9));
        System.out.println();// 换行
        System.out.print("插入不重复的数据 1：" + binarySearchTree.insert(1));
        System.out.println();// 换行
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        binarySearchTree.remove(19);
        System.out.print("删除元素 19 ：");
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        System.out.print("查找不存在的数据50 ：");
        System.out.println(binarySearchTree.search(50));
        System.out.print("查找存在的数据 7：");
        System.out.println(binarySearchTree.search(7));
    }
}

Analyse des performances

   Les opérations d'insertion et de suppression doivent être recherchées en premier, et l'efficacité de la recherche représente la performance de chaque opération. dans les performances de l'arbre de recherche binaire.
 
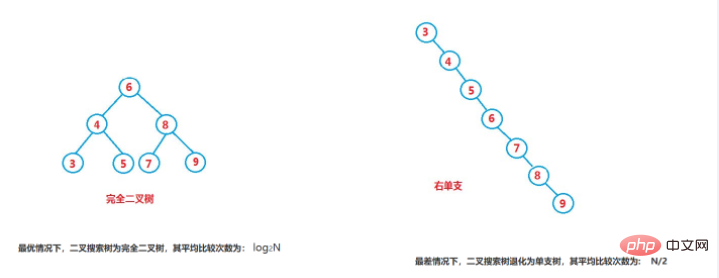
  Pour un arbre de recherche binaire à n nœuds, si la probabilité de trouver chaque élément est égale, alors la longueur moyenne de recherche de l'arbre de recherche binaire est fonction de la profondeur du nœud dans la recherche binaire arbre, C'est-à-dire que plus le nœud est profond, plus le nombre de comparaisons est grand.
 
  Mais pour un même jeu de codes clés, si l'ordre d'insertion de chaque code clé est différent, des arbres de recherche binaires avec des structures différentes peuvent être obtenus :

Si nous pouvons garantir la gauche et la droite enfants de l'arbre de recherche binaire La différence de hauteur de l'arbre ne dépasse pas 1. Essayez de respecter les conditions d'équilibre élevé.
Cela devient un arbre AVL (arbre de recherche binaire équilibré en hauteur). L'arbre AVL présente également des inconvénients : il nécessite des rotations fréquentes. Beaucoup d’efficacité gaspillée.
À ce stade, l'arbre rouge-noir naît pour éviter davantage de rotations.

La relation entre les ensembles de classes Java

TreeMap et TreeSet sont Map et Set implémentés à l'aide d'arbres de recherche en Java ; en fait, des arbres rouge-noir sont utilisés, et les arbres rouge-noir sont un arbre de recherche binaire approximativement équilibré, c'est-à-dire est, basé sur l'arbre de recherche binaire + la couleur et la vérification des propriétés de l'arbre rouge-noir. Concernant le contenu de l'arbre rouge-noir, le blogueur écrira un blog après l'avoir appris.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!