Maison >Périphériques technologiques >IA >Cui Peng, Université Tsinghua : Cadre et pratique décisionnels intelligents et dignes de confiance
Cui Peng, Université Tsinghua : Cadre et pratique décisionnels intelligents et dignes de confiance
- 王林avant
- 2023-05-06 21:10:081455parcourir

1. Un cadre décisionnel intelligent et fiable
Tout d'abord, j'aimerais partager avec vous un cadre décisionnel intelligent et fiable.
1. Des décisions qui sont plus importantes que des prédictions
Dans de nombreux scénarios réels, les décisions sont plus importantes que les prédictions. Parce que le but de la prédiction elle-même n’est pas seulement de prédire à quoi ressemblera l’avenir, mais d’influencer certains comportements et décisions clés du présent grâce à la prédiction.
Dans de nombreux domaines, y compris celui de la sociologie d'entreprise, la prise de décision est très importante, comme la croissance continue de l'entreprise (Croissance continue de l'entreprise), la découverte de nouvelles opportunités d'affaires (Nouvelles opportunités d'affaires), etc. prendre de meilleures décisions grâce aux données. Soutenir correctement la décision finale fait partie du travail dans le domaine de l'intelligence artificielle qui ne peut être ignoré.

2. La prise de décision partout

Les scénarios de prise de décision sont partout. Le système de recommandation bien connu, qui recommande un produit à un utilisateur, prend en réalité une décision de sélection parmi tous les produits. Les algorithmes de tarification dans le commerce électronique, tels que la tarification des services logistiques, etc., comment fixer un prix raisonnable pour un service ; dans des scénarios médicaux, quels médicaments ou traitements doivent être recommandés en fonction des symptômes du patient, ce sont tous des processus décisionnels interventionnels. scénarios.
3. Méthodes courantes de prise de décision 1 : Utiliser des simulateurs pour prendre des décisions
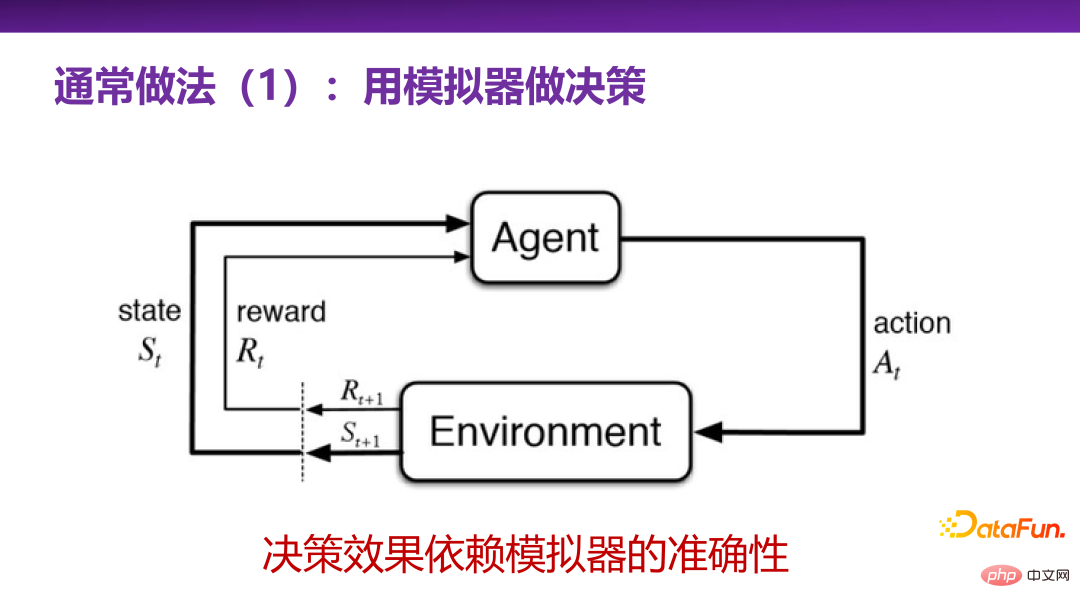
Le monde universitaire et l'industrie ne sont pas familiers avec la prise de décision, et il existe certaines méthodes couramment utilisées pour résoudre ou discuter problèmes de prise de décision, pour résumer, il existe deux méthodes courantes.
La première approche courante consiste à utiliser un simulateur pour prendre des décisions, c'est-à-dire l'apprentissage par renforcement. L'apprentissage par renforcement est une méthode très puissante pour prendre des décisions.Il équivaut à avoir une scène réelle (environnement) ou une simulation d'une scène réelle, à travers laquelle un agent intelligent peut continuellement effectuer un apprentissage par essais et erreurs avec la scène réelle. explorez les actions clés (actions), et enfin trouvez les actions clés avec la plus grande récompense (récompense) dans ce scénario réel.
L'ensemble du système décisionnel de l'apprentissage par renforcement sera la première chose à laquelle tout le monde pensera dans de nombreux problèmes d'application pratique. Mais dans des scénarios d’application réels, le plus grand défi lié à l’utilisation de l’apprentissage par renforcement est de savoir s’il existe un bon simulateur pour les scénarios réels. La construction du simulateur lui-même est une tâche difficile. Bien entendu, pour des scénarios de jeu tels que les échecs Alphago, les règles sont généralement relativement fermées et il est relativement facile de construire un simulateur. Cependant, dans les affaires et dans la vie réelle, la plupart d’entre eux sont des scénarios ouverts, comme la conduite sans conducteur, et il est difficile de proposer un simulateur très complet. Construire un simulateur nécessite une compréhension très approfondie du scénario. Par conséquent, construire un simulateur lui-même peut être un problème plus difficile que prendre des décisions et faire des prédictions. Il s’agit en fait d’une limitation de l’apprentissage par renforcement.
4. Approche commune de prise de décision 2 : Utiliser des prédictions pour prendre des décisions
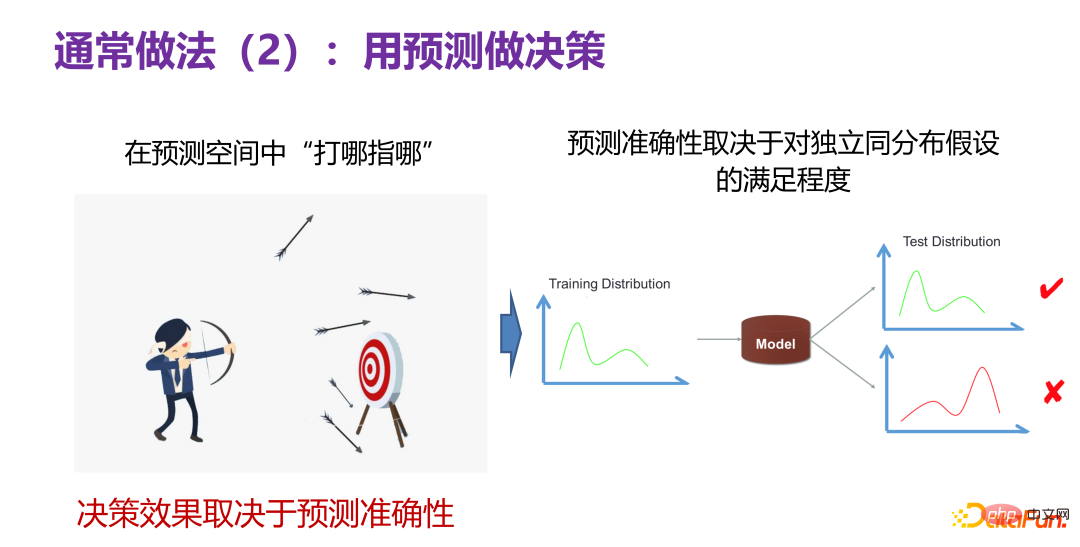
Une autre approche courante consiste à utiliser des prédictions pour prendre des décisions. Cela signifie que même si nous ne savons pas quel type de décision est bonne maintenant, s'il existe un prédicteur, il peut « déterminer où pointer » dans l'espace de prédiction, comme le montre le côté gauche de la figure ci-dessous. personne tirant une flèche, vous pouvez d'abord tirer quelques flèches lorsque vous tirez sur une cible, si vous découvrez quelle flèche tire le mieux, vous pouvez utiliser le comportement clé de cette flèche pour prendre des décisions pertinentes. S’il existe un tel espace de prédiction, les prédictions peuvent être utilisées pour prendre des décisions.
Mais l'effet de la prise de décision dépend de l'exactitude de l'espace de prédiction, que la prédiction soit exacte ou non. Bien que dans l'espace de prédiction, la cible soit atteinte 10 fois, lorsqu'elle est appliquée à la vie ou aux produits réels, le nombre d'atteintes est de 0, ce qui signifie que l'espace de prédiction est inexact. Jusqu'à présent, le scénario le plus fiable dans les tâches de prédiction consiste à faire des prédictions sous l'hypothèse d'une distribution indépendante et identique, c'est-à-dire que la distribution de test et la distribution d'entraînement sont la même distribution. Il existe actuellement de nombreuses prédictions puissantes Modèle (modèle de prédiction). ) peut bien résoudre des problèmes pratiques. Cela nous indique : Le fait que la précision de la prédiction soit bonne ou non dépend dans une certaine mesure du fait que la distribution des données de test et des données d'entraînement dans le scénario réel satisfait une distribution indépendante et identique.
Continuez à réfléchir profondément à l'exactitude des prédictions. Supposons qu'un modèle de prédiction soit construit sur la base de données historiques P(X,Y), puis nous explorons les avantages apportés par différents comportements clés, c'est-à-dire tirer plusieurs flèches comme mentionné ci-dessus pour voir laquelle a le plus grand nombre de cibles. . En le décomposant, on peut le diviser en deux situations différentes.
La première catégorie consiste à optimiser la valeur d'une variable de décision donnée. Si vous savez à l'avance laquelle des variables d'entrée X est une meilleure variable de décision, par exemple, si le prix est une variable de décision dans Que se passe-t-il une fois la valeur obtenue.
L'autre catégorie consiste à rechercher les variables de décision optimales et à optimiser leurs valeurs. On ne sait pas à l'avance laquelle des valeurs prédites par le modèle de prédiction est la bonne.
Sur la base de cette hypothèse de prémisse, lors du changement de la valeur de la variable de décision, P(X) est réellement modifié, c'est-à-dire que si P(X) change, P(X,Y) changera définitivement, puis indépendamment et simultanément. L’hypothèse de distribution elle-même s’effondre, ce qui signifie que les prédictions sont en réalité très probablement invalides. Par conséquent, si le problème de prise de décision est résolu de manière prédictive, cela déclenchera le problème de la généralisation hors distribution, car la modification de la valeur de la variable de décision entraînera inévitablement un changement de distribution. Dans le cas d'un écart de distribution, comment faire des prédictions appartient au problème de prédiction de la généralisation hors distribution et n'est pas le sujet de l'article d'aujourd'hui. Si le problème de prédiction de la généralisation hors distribution peut être résolu dans le domaine de la prédiction, l'utilisation de la prédiction pour prendre des décisions est également l'une des voies réalisables. Cependant, l’utilisation actuelle de méthodes d’identification (In-Distribution) ou de prédiction directe (prédiction directe) pour prendre des décisions est théoriquement invalide et problématique.
5. Les problèmes de prise de décision entrent dans la catégorie des causes et des effets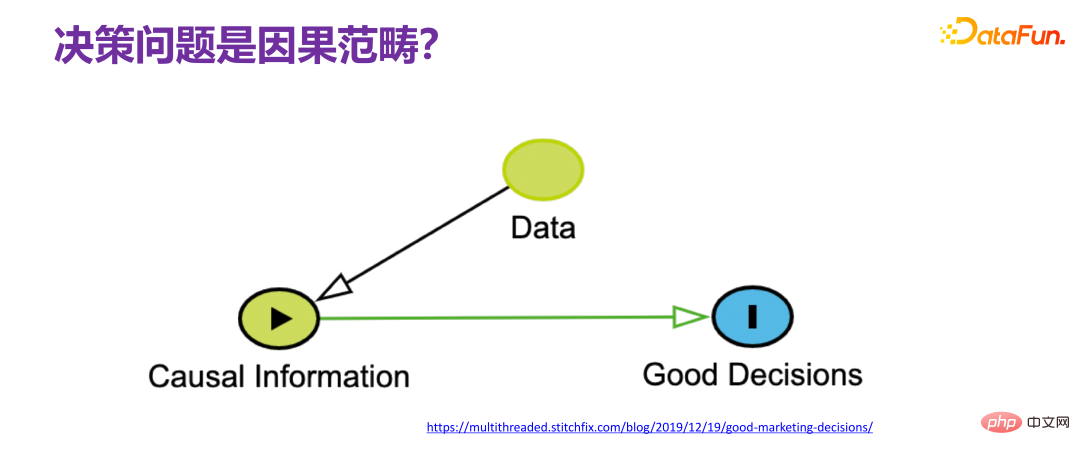
Quand on parle de problèmes de prise de décision, le problème de prise de décision est généralement directement lié à la cause et à l'effet. La soi-disant prise de décision fait référence au type de décision à prendre. Nous devons nous demander pourquoi une telle décision a été prise. Il est évident qu'il existe une chaîne de cause à effet. Le consensus de nombreux chercheurs dans la communauté universitaire est. que pour résoudre les problèmes de prise de décision, nous ne pouvons pas éviter la cause et l'effet, c'est-à-dire que nous devons partir de données observables. Obtenir suffisamment d'informations causales (informations causales) et comprendre le mécanisme causal pertinent (mécanisme causal), puis concevoir des stratégies pour. prise de décision finale basée sur le mécanisme causal. Si nous pouvons comprendre complètement l'ensemble du processus, nous pouvons parfaitement restaurer l'ensemble du mécanisme causal, donc la prise de décision ne constitue pas un problème, car elle équivaut en fait à avoir la perspective de Dieu, et il n'y a aucun défi dans la prise de décision.
6. Une description cadre de la prise de décisionDès 2015, Jon Kleinberg a publié dans un article : Les problèmes de prise de décision ne sont pas résolus par des mécanismes causals, c'est-à-dire que toutes les décisions ne nécessitent pas mécanismes causals à résoudre. Jon Kleinberg est un professeur bien connu à l'Université Cornell. Le célèbre algorithme des hits, la théorie du style à six degrés, etc. sont tous les résultats des recherches de Jon Kleinberg. Jon Kleinberg a publié un article sur les problèmes de prise de décision en 2015, « Prediction Policy Problems »[1]. Il pensait que certains problèmes de prise de décision sont des problèmes de stratégie de prédiction, et pour prouver cet argument, il a donné une description cadre de la prise de décision, comme le montre la figure ci-dessous.
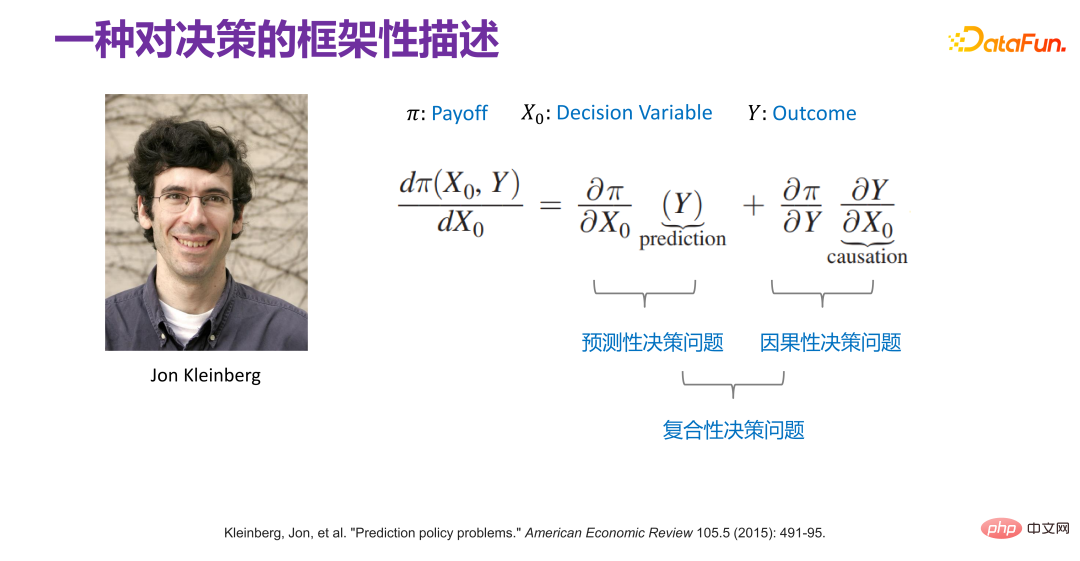
Π est la fonction de paiement, x0 est causée par les variables de décision Résultat, Π est en fait une fonction de x0 et Y. Alors, comment x0 change-t-il ? Si Π est le plus grand, vous pouvez trouver une telle dérivée : 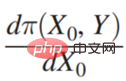
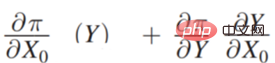
7. Deux cas de scénarios de prise de décision

Comme le montre la figure ci-dessus, les deux scénarios de prise de décision sont les suivants, où x0 est la variable de décision. Les définitions dans les deux scénarios sont différentes.
Premier regard sur le cas de scène à gauche. Il n'y a aucune relation entre le fait que vous deviez apporter un parapluie et s'il pleut, c'est-à-dire que x0 et Y ne sont pas liés et sont introduits dans 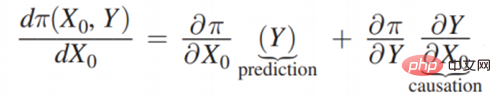
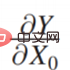
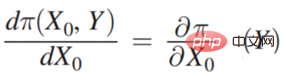
Le cas à droite est que si vous êtes un chef, devriez-vous payer quelqu'un pour faire la Danse de Dieu afin de prier pour la pluie ? En fait, cela dépend en grande partie de la capacité de la « Danse de la Danse » à apporter de la pluie et si cela a un effet causal. 
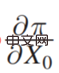
Grâce aux deux scénarios de prise de décision réels ci-dessus, les problèmes de prise de décision peuvent être divisés en deux catégories : la prise de décision prédictive et la prise de décision causale, et le cadre des problèmes de prise de décision donné par Jon Kleinberg explique également très bien l'importance de la prise de décision.
8. La complexité de la prise de décision

L'un des points de vue exprimés dans l'article de Jon Kleinberg est que pour les problèmes de prise de décision prédictive, il importe seulement que la prédiction soit bonne ou non, et le mécanisme causal n'est pas nécessairement nécessaire. Oui, le modèle de prédiction est très utile dans les scénarios de prise de décision, a une bonne capacité d'expression pour les problèmes de prise de décision et peut intégrer de nombreuses situations ensemble. Mais la complexité réelle de la prise de décision dépasse la compréhension antérieure des scénarios de prévision. Dans la plupart des cas, lors de la résolution de problèmes de prédiction, nous faisons simplement de notre mieux (meilleur effort), essayons d'utiliser des modèles plus complexes et plus de données, dans l'espoir d'améliorer la précision finale, c'est-à-dire le modèle du meilleur effort (modèle du meilleur effort) .
Mais il y a bien plus de contraintes dans les scénarios de prise de décision que de prédictions. La prise de décision est en fait le dernier kilomètre. La décision finale affectera en effet tous les aspects, affectera de nombreuses parties prenantes et impliquera des facteurs sociaux et économiques très complexes. Par exemple, dans le cadre d’un même prêt, la question de savoir s’il existe une discrimination à l’égard de personnes de sexes différents et de régions différentes est une question typique d’équité algorithmique. Le Big Data est familier et le même produit a des prix différents pour différentes personnes, ce qui constitue également un problème. Ces dernières années, tout le monde a une compréhension approfondie du cocooning d'informations, qui consiste à recommander en permanence un utilisateur en fonction de ses intérêts ou de ses intérêts dans un spectre relativement étroit, ce qui formera une salle de cocooning d'informations. Si les choses continuent ainsi, de mauvais phénomènes culturels et sociaux apparaîtront. Par conséquent, lors de la prise de décisions, davantage de facteurs doivent être pris en compte pour prendre des décisions crédibles.
9. Un cadre pour une prise de décision intelligente et fiable
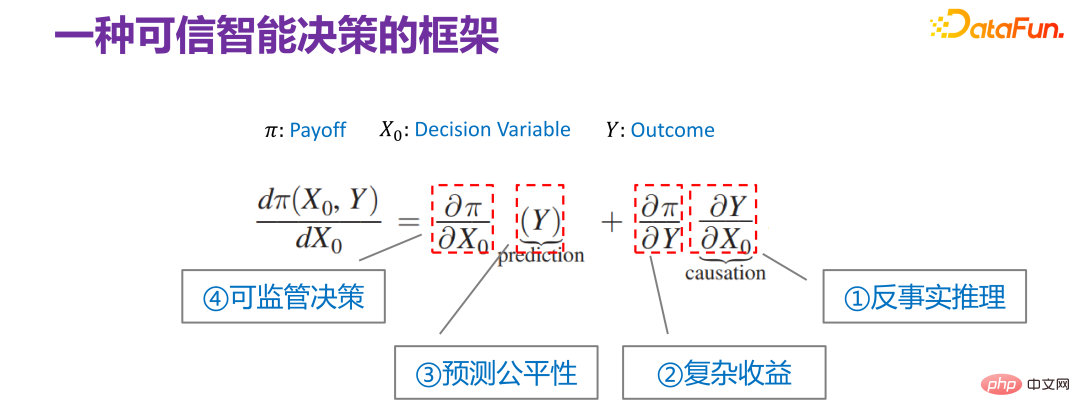
Continuez à interpréter le cadre des problèmes de prise de décision donné par Jon Kleinberg du point de vue de la fiabilité de la prise de décision. Bien que Jon Kleinberg lui-même ait proposé ce cadre de problèmes de prise de décision pour plaider en faveur de l'efficacité du modèle de prédiction pour les problèmes de prise de décision, la connotation du cadre de problèmes de prise de décision est en fait très riche. Voici une explication de chaque élément du cadre de problèmes de prise de décision. cadre de problème de prise de décision.
Tout d'abord est l'élément le plus à droite : 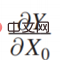
est en fait équivalent à la relation entre la fonction de revenu et les résultats du modèle. Il existe des scénarios plus simples pour la relation entre Y et Π. Par exemple, lors de la recommandation de produits, quels types de produits sont recommandés aux utilisateurs et les utilisateurs cliquent dessus ? La fonction de gain optimisée finale est en fait le taux de clics global. Il s’agit d’un scénario où la relation entre les deux est relativement simple. Cependant, dans la réalité des affaires, que ce soit du point de vue de la plateforme ou de la réglementation, la relation entre Y et Π est très compliquée dans la plupart des cas. Par exemple, dans un cas qui sera abordé plus tard, lors de l'optimisation des revenus de la plateforme, vous ne pouvez pas seulement regarder le taux de clics actuel, mais aussi les revenus à long terme. La relation entre Y et Π sera relativement compliquée, c'est-à-dire des revenus complexes.
Le troisième élément est Y. La tâche principale est de faire des prédictions, mais si la prédiction est utilisée pour prendre des décisions et que le scénario de prise de décision est de nature sociale, comme affecter le crédit personnel, cela affecte si l'examen d'entrée à l'université est admis, si le prisonnier sera libéré, etc., alors toutes ces tâches dites prédictives exigent que la prédiction soit juste et ne puisse pas utiliser certaines variables dimensionnelles sensibles, telles que le sexe, la race, l'identité, etc. pour faire des prédictions.
Le quatrième élément est : 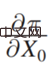
Ce cadre de problèmes de prise de décision contient des scénarios à différents niveaux, et il peut également être considéré comme ayant les quatre sous-directions différentes ci-dessus. Mais en général, les quatre sous-directions ci-dessus sont très liées à une prise de décision crédible, c'est-à-dire que si vous voulez vous assurer que le personnage est crédible, tous les aspects des facteurs doivent être pris en compte. Mais d’une manière générale, elle peut s’exprimer de manière uniforme en utilisant le cadre donné par Jon Kleinberg.
Ce qui suit présentera les quatre sous-directions du cadre de prise de décision intelligente et digne de confiance : le raisonnement contrefactuel, les avantages complexes, l'équité prédictive et la prise de décision réglementaire.
2. Le raisonnement contrefactuel dans la prise de décision intelligente et fiable
Tout d'abord, nous présenterons quelques réflexions et pratiques sur le raisonnement contrefactuel dans le cadre d'une prise de décision intelligente et fiable.

1. Raisonnement contrefactuel

Il existe trois scénarios dans le raisonnement contrefactuel.
La première est l'évaluation de l'effet moyen de la stratégie (Off-Policy Evaluation). Pour une politique donnée, nous ne souhaitons pas effectuer de tests AB car le coût des tests AB est trop élevé. Par conséquent, évaluer l'effet de la politique sur les données hors ligne équivaut à tester l'ensemble de la population, comme un échantillon. évaluation globale de l’effet pour tous les groupes d’utilisateurs.
La seconde est l'évaluation des effets individuels de la stratégie (prédiction contrefactuelle), qui consiste à prédire l'effet de la stratégie à un niveau individuel. Il ne s'agit pas d'une stratégie globale de plateforme, mais quel type d'effet y aura-t-il après un certain point. l'intervention est réalisée pour un particulier.
Le troisième est l'optimisation des politiques, c'est-à-dire comment sélectionner la meilleure intervention pour un individu. Contrairement à la prédiction des effets individuels, la prédiction des effets individuels consiste d'abord à savoir comment intervenir, puis à prédire l'effet après l'intervention. L'optimisation de la stratégie ne consiste pas à savoir à l'avance comment intervenir, mais à découvrir comment obtenir le meilleur effet après l'intervention.
2. Évaluation de l'effet moyen de la stratégie(1) Aperçu du cadre problématique de l'évaluation de l'effet moyen de la stratégie
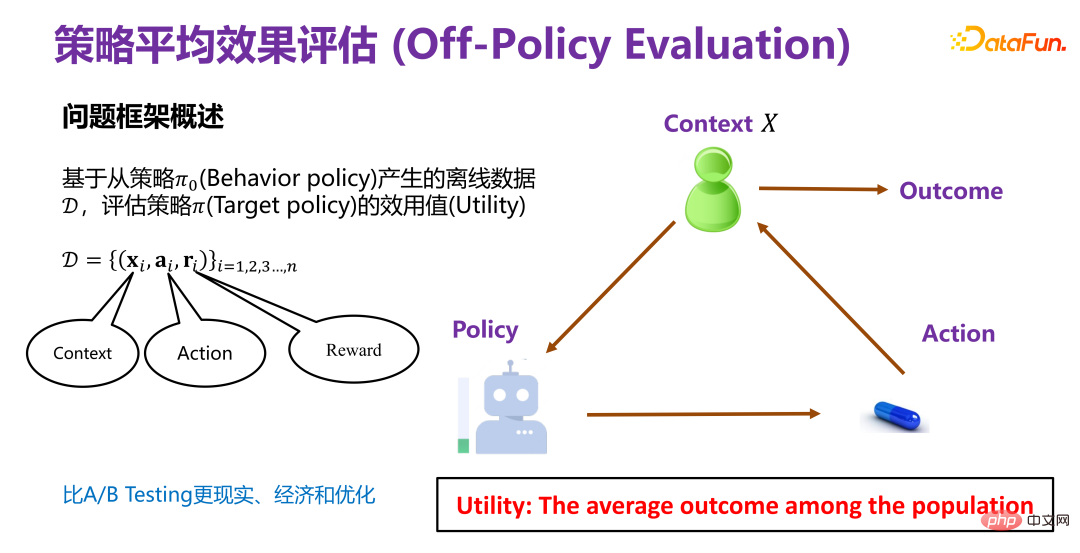
L'évaluation de l'effet moyen de la stratégie est basée sur la stratégie Π 0 Les données hors ligne D générées par (Politique de comportement) évaluent la valeur d'utilité (Utilité) de la politique Π (Politique cible). Π0 est une stratégie existante, telle que la stratégie de recommandation qui a été utilisée dans les systèmes de recommandation existants. Les données hors ligne D générées dans le cadre de la stratégie existante contiennent au moins trois dimensions, comme le montre la figure ci-dessus, xi sont les informations de base (contexte), telles que les utilisateurs et les produits dans le système de recommandation Les attributs de Ou acheter des biens. Évaluez la valeur d'utilité (Utilité) d'une nouvelle politique Π (Politique cible) sur la base de données historiques. Ainsi, le cadre général est que dans un certain contexte, une certaine stratégie (politique) aura une variable de comportement ou d'intervention correspondante (traitement). Lorsque cette variable d'intervention (traitement) est déclenchée, elle produira des résultats correspondants. Parmi eux, la valeur d'utilité (Utility) est le gain susmentionné. Dans le principe de simplification, la valeur d'utilité est la somme des résultats générés par tous les utilisateurs, ou l'effet moyen. (2) Méthodes existantes d'évaluation de l'effet moyen de la stratégie La méthode traditionnelle d'évaluation de l'effet moyen de la stratégie est basée sur la méthode de prédiction des résultats (méthode directe), dans le cadre de la nouvelle politique (politique) donnée xi, pour le sujet, il est recommandé d'exposer ou de ne pas exposer, c'est-à-dire le comportement correspondant Il faut prédire si l'utilisateur final achètera ou cliquera si l'exposition est réalisée, c'est-à-dire le résultat final (récompense). ). Mais veuillez noter que la récompense est en réalité une fonction de prédiction, obtenue grâce à des données historiques. La distribution conjointe (distribution conjointe) de x, a et r dans les données historiques a en fait été générée sous Π0. Maintenant, la distribution des données générée par Π est modifiée et le modèle de prédiction de distribution conjointe (prédiction de distribution conjointe) généré sous le Π0 d'origine est. modèle utilisé) pour faire des prédictions, il est évident qu'il s'agit d'un problème OOD (hors distribution). Si un modèle de prédiction OOD est utilisé ultérieurement, le problème de décalage de distribution des données peut être atténué si un modèle ID (in-distribution). ) un modèle de prédiction est utilisé, en principe il y aura certainement des problèmes. Il s’agit de la méthode traditionnelle d’évaluation de l’efficacité moyenne des stratégies.
(3) Nouvelle méthode d'évaluation de l'effet moyen des stratégies : estimateur FCB

ai
) de chaque groupe d'action correspondant est généralement cohérente avec P(X).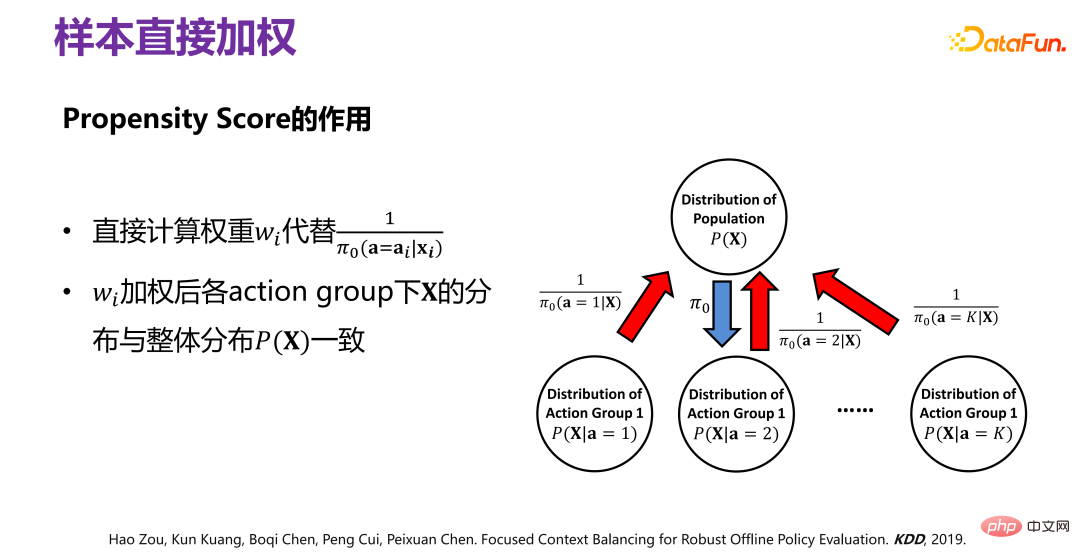
Les données historiques sont générées à partir de Π0. Pour supprimer le biais de distribution (biais) causé par Π0, la méthode spécifique est celle indiquée dans la figure ci-dessus. La distribution des données d'origine P (X. ), sous l'action de Π0, cela équivaut à diviser P(X) en plusieurs sous-distributions P(X|a=1), P(X|a=2), P(X|a =3),...,P(X|a=K), c'est-à-dire un sous-ensemble de P(X) correspondant à différents comportements. Il y a un facteur Π0 sous chaque groupe de comportements. . Pour éliminer l'écart provoqué par , vous pouvez repondérer les données historiques générées par Π0 afin que toutes les sous-distributions après pondération soient proches de la distribution d'origine P(X), c'est-à-dire l'échantillon directement pondéré. .
Prédire quel sera l'effet final d'une nouvelle stratégie sur la base de données historiques nécessite deux étapes. Comme mentionné ci-dessus, la première étape consiste à supprimer le biais provoqué par la stratégie originale Π0 en pondérant directement les échantillons. La deuxième étape consiste à prédire l'effet de la nouvelle stratégie Π, c'est-à-dire à estimer l'effet final en fonction de l'écart provoqué par la nouvelle stratégie Π, il faut donc ajouter l'écart provoqué par la nouvelle stratégie Π 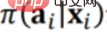
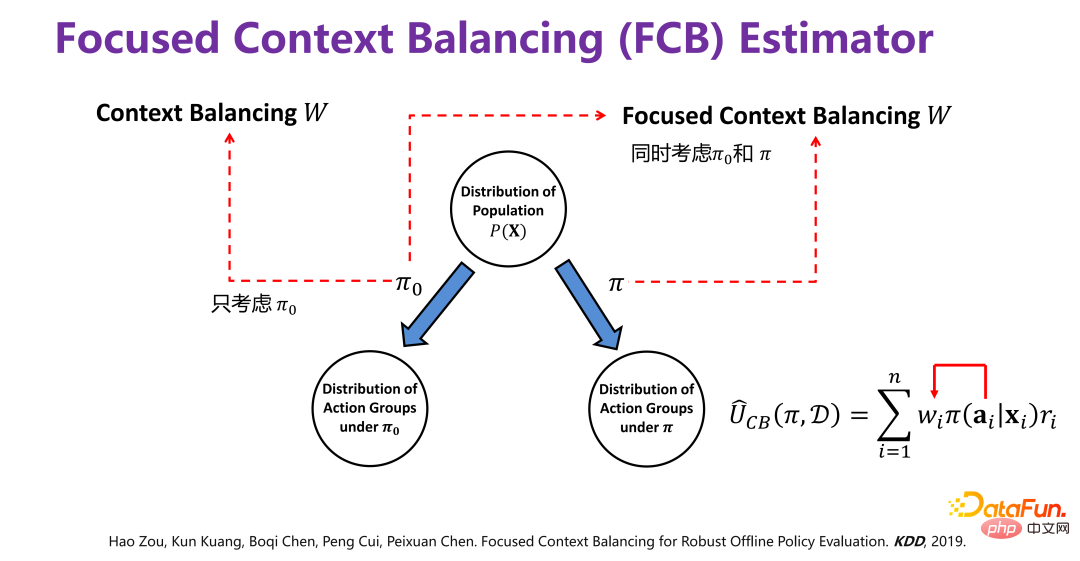
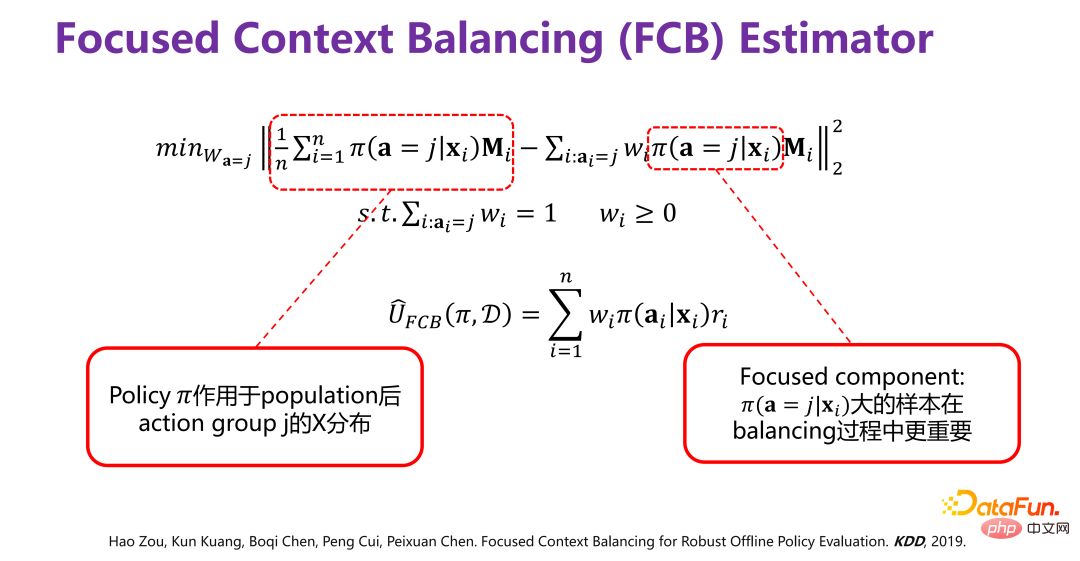
Par conséquent :
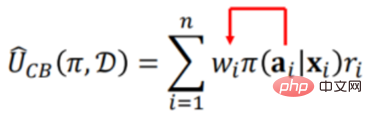
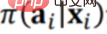
équivaut à En ajoutant l'écart de la nouvelle stratégie, l'effet final d'une nouvelle stratégie peut être prédit. La méthode spécifique ne sera pas décrite en détail, mais vous pouvez vous référer à l'article [2].
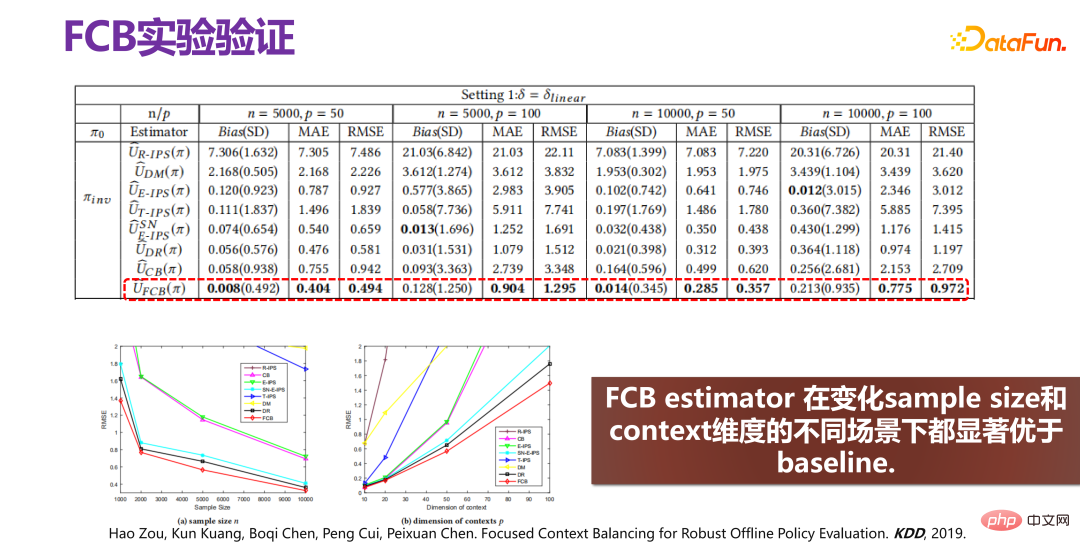
L'effet d'amélioration final de la nouvelle méthode FCB Estimator est montré dans la figure ci-dessus. L'effet d'amélioration est très évident, que ce soit en termes de biais ou de RMSE, l'amélioration relative est d'environ 15. %-20%. L'estimateur FCB est nettement meilleur que la référence dans différents scénarios avec des tailles d'échantillon et des dimensions de contexte variables. Des articles connexes ont été publiés dans KDD 2019 [2].
3. Stratégie de prédiction des effets individuels
(1) Description globale de la stratégie de prédiction des effets individuels
La stratégie de prédiction des effets individuels consiste à prendre pleinement en compte l'hétérogénéité individuelle et à mettre directement en œuvre une intervention différenciée pour les individus, c'est-à-dire , en respectant la volonté individuelle et en mettant en œuvre différentes interventions pour différents individus.
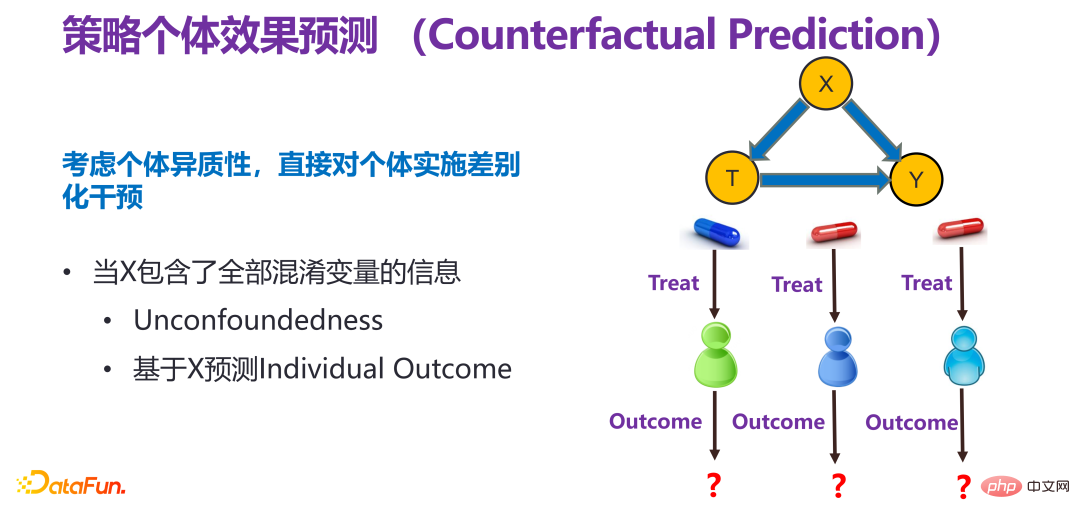
(2) Limites des méthodes existantes
La méthode courante pour prédire l'effet individuel des stratégies consiste à effectuer directement une modélisation prédictive sur les individus, c'est-à-dire sur la base de données d'observation historiques : 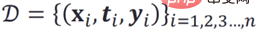

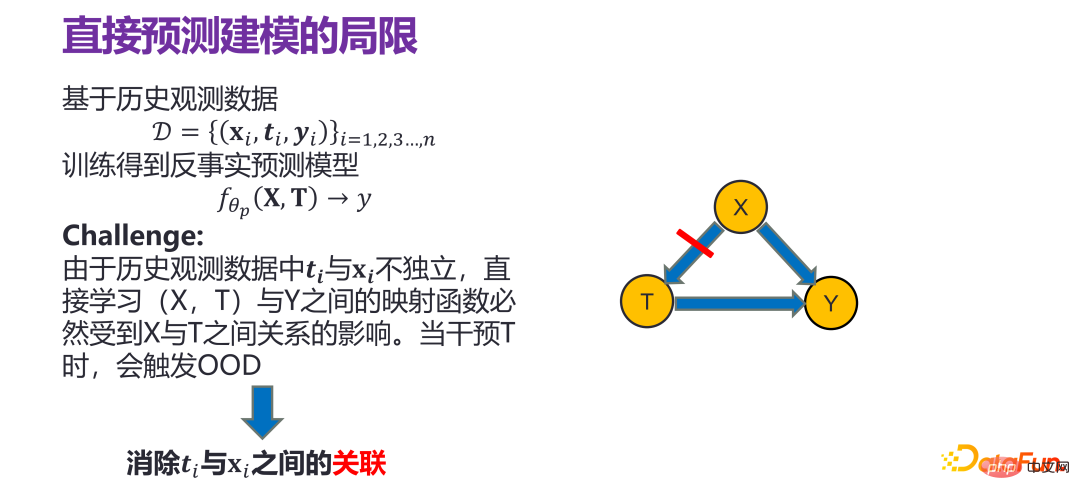
Si vous effectuez une analyse de régression ou des modèles similaires directement sous la distribution des données historiques, il y aura des problèmes. Parce que ti et xi dans les données d'observation historiques ne sont pas indépendants, l'apprentissage direct de la fonction de cartographie directe entre (X, T) et Y sera inévitablement affecté par la relation entre X et T, qui est tout à fait Étant donné un xi, il doit y avoir un ti correspondant dans les données historiques. Par exemple, ti doit être égal à 0. Lors d'une intervention dans T, par exemple, si. vous forcez t i est changé en 1, ce qui en fait n'obéit plus à la distribution historique d'origine, ce qui signifie que le modèle de prédiction ID (In-Distribution) construit sous la distribution des données historiques n'est pas valide et déclenche OOD (Out-of -Distribution) ).
Par conséquent, lors de la construction du modèle dit de prédiction, il est nécessaire d'éliminer la corrélation entre X et T, et d'estimer respectivement l'impact de X sur Y et l'impact de T sur Y. si T intervient ou change, cela n'a rien à voir avec X. L'impact et le changement que cela aura sur Y est entièrement déterminé par le lien T->Y, et il n'y a pas de problème OOD (Out-of-Distribution).

L'approche traditionnelle consiste à utiliser la méthode de repondération de l'échantillon (Sample Re-weighting) pour supprimer l'association entre X et T. Il existe deux méthodes : (1) Propension inverse pondération des scores, (2) équilibrage variable. Ces méthodes ont cependant des limites : elles ne conviennent qu’à des types simples de scénarios de variables d’intervention (traitement), à valeurs binaires ou discrètes. Dans les scénarios d'application réels, tels que les systèmes de recommandation, la variable intermédiaire (traitement) a une dimension élevée. Les produits sont recommandés aux utilisateurs, et ce qui est recommandé est un ensemble, c'est-à-dire que les recommandations sont faites à partir de nombreux produits. Lorsque la dimension de la variable intermédiaire (traitement) est très élevée, l'utilisation de méthodes traditionnelles pour corréler directement la variable intermédiaire initiale (traitement brut) et la variable de confusion (confondeur) X est très complexe, et même l'espace d'échantillonnage n'est pas suffisant pour prendre en charge la dimension élevée. La variable intermédiaire (traitement).
(3) Nouvelle méthode de prédiction de l'effet individuel de la stratégie : VSR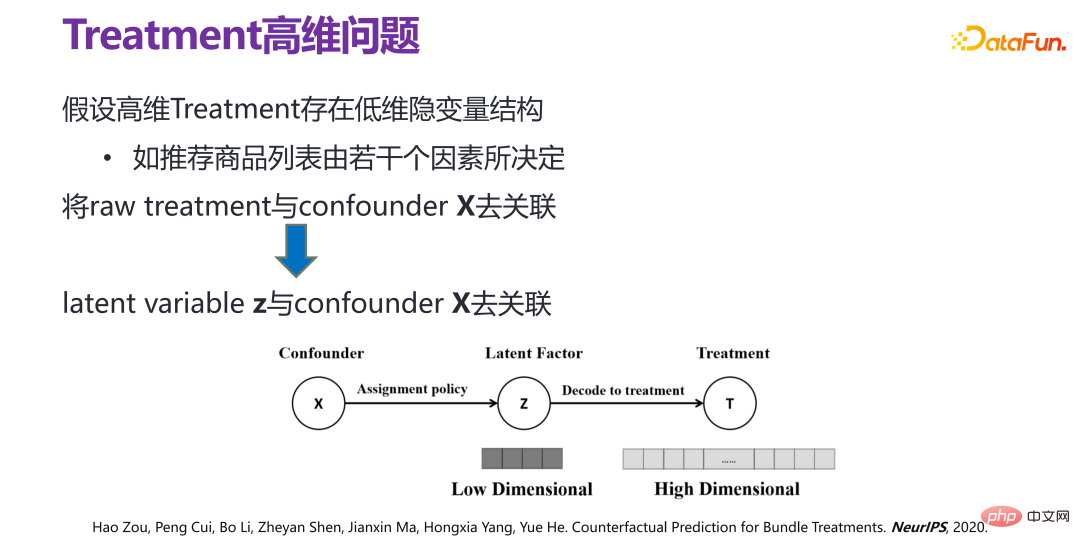
Si l'on suppose que la variable intermédiaire de grande dimension (traitement) a une structure de variable latente de faible dimension , c'est-à-dire de grande dimension. En principe, la variable intermédiaire (traitement) n'est pas aléatoire. Par exemple, dans un système de recommandation, un ensemble de produits recommandés par une stratégie de recommandation donnée a diverses relations entre les produits et il existe de faibles relations. variables dimensionnelles cachées. La structure des variables, c'est-à-dire la liste de produits recommandés, est déterminée par plusieurs facteurs.
S'il existe une variable latente z sous la variable intermédiaire de haute dimension (traitement), le problème peut en fait être transformé en décorrélation entre x et z, c'est-à-dire avec le facteur latent (facteur latent ) ). De cette manière, le traitement des faisceaux peut être réalisé avec un espace d’échantillon limité. Une nouvelle méthode VSR est donc proposée. Dans la méthode VSR , la première est l'apprentissage de la variable latente z (variable latente z) de la variable d'intervention de grande dimension (traitement), c'est-à-dire à l'aide d'un auto-encodeur variationnel (VAE) pour apprentissage ; puis la fonction de poids Dans l'apprentissage de w (x, z), la décorrélation entre x et z est réalisée par repondération d'échantillon, enfin, un modèle de régression peut être obtenu directement en utilisant le modèle de régression sous la distribution de corrélation repondérée ; modèle de prédiction relativement idéal pour l’effet individuel des stratégies. 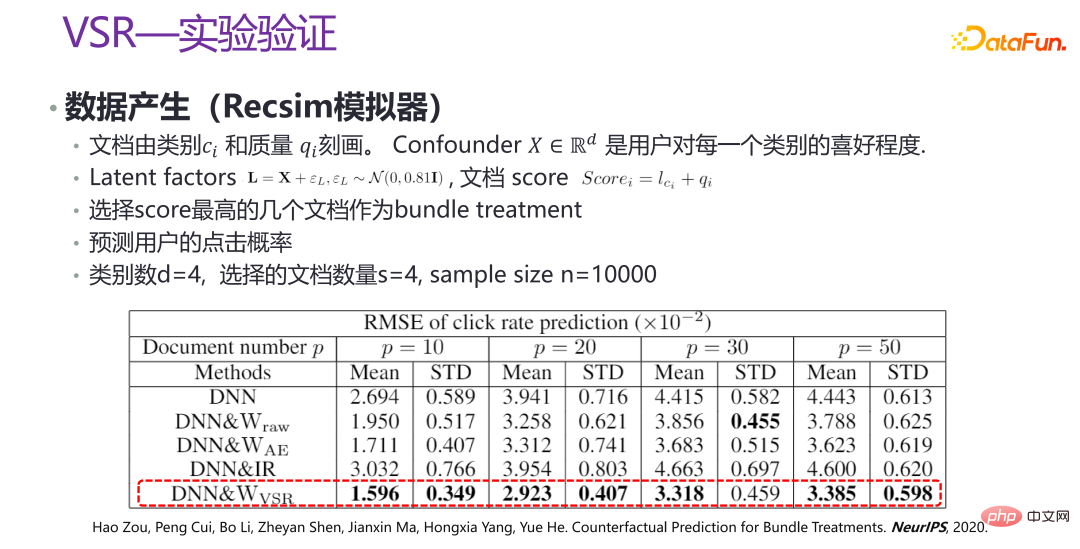
# 🎜 🎜#L'image ci-dessus est la vérification expérimentale de la nouvelle méthode VSR. Dans certains scénarios, certaines données sont générées via le simulateur Recsim, ainsi que des données simulées artificiellement pour vérification. On peut voir que sous différentes valeurs de p, les performances du VSR sont relativement stables, ce qui est grandement amélioré par rapport aux autres méthodes. Des articles connexes ont été publiés dans NeurIPS 2020 [3].
4. Optimisation de la stratégie
 #🎜 🎜#
#🎜 🎜#
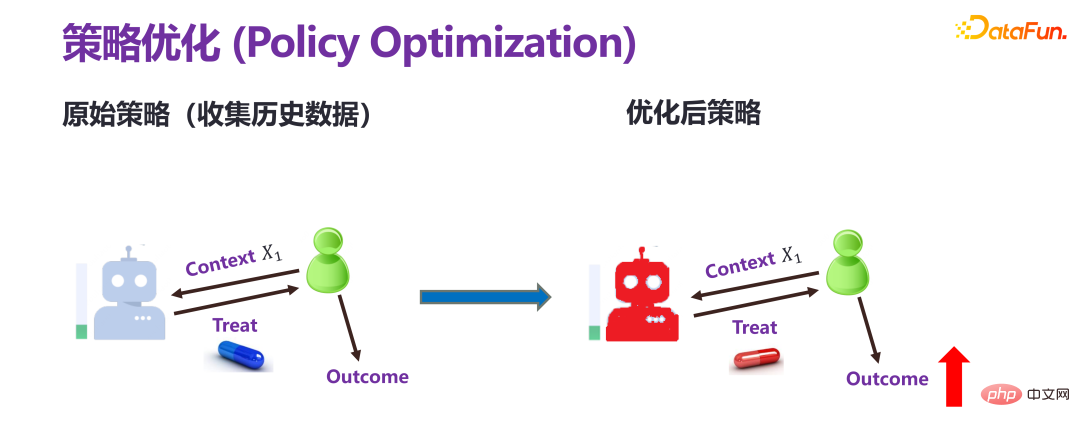
Il existe une différence fondamentale entre l'optimisation de la stratégie et les deux évaluations de prédiction précédentes. L'évaluation prédictive consiste à donner à l'avance une stratégie (politique) ou une intervention personnalisée (traitement individuel) pour prédire le résultat final. L’optimisation stratégique, également appelée apprentissage stratégique, n’a qu’un seul objectif : obtenir de meilleurs résultats. Par exemple, si le revenu doit augmenter, quel type d’intervention doit être mis en œuvre.
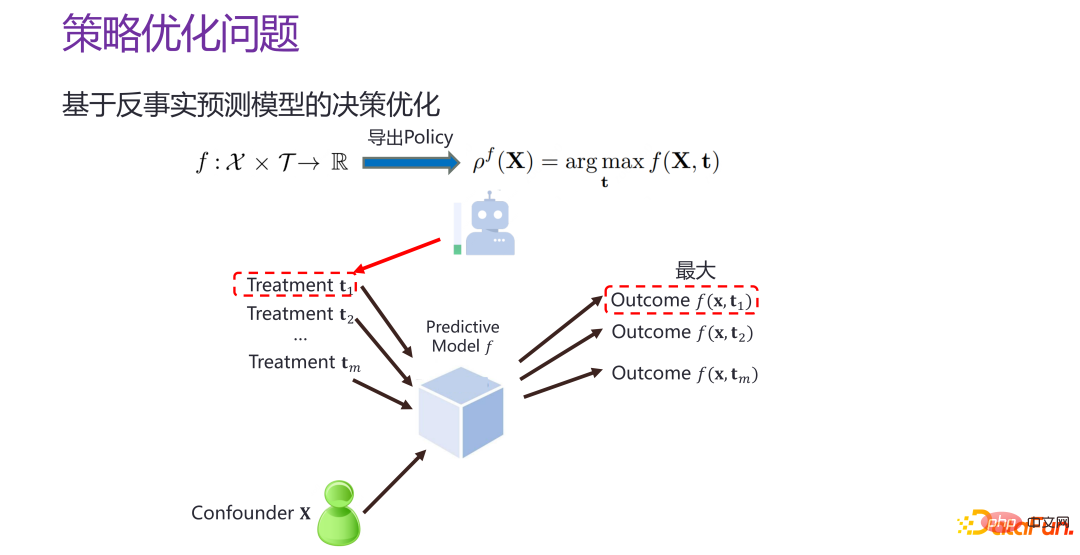
S'il y a un contrefactuel maintenant Le modèle de prédiction au niveau individuel f, c'est-à-dire le modèle de prédiction des effets individuels de la stratégie f, est donné xi et t#🎜 🎜 #i, vous pouvez estimer le résultat correspondant, puis vous pouvez parcourir T. Quand t prend quelle valeur, la valeur de f est la plus grande. Cela équivaut à construire un meilleur espace de prédiction et à « cibler où frapper » dans l'espace de prédiction.
Mais il y a un problème à réduire le problème d'optimisation de la stratégie à la construction d'un modèle de prédiction de l'effet individuel de la stratégie. L'objectif de la prédiction des effets individuels des stratégies, comme mentionné ci-dessus, équivaut en fait à donner une intervention, en espérant que l'erreur entre la situation contrefactuelle prédite et la situation réelle soit aussi petite que possible, et pour toutes les interventions données, nous espérons comparer précis. Le but de l'optimisation de la stratégie est de trouverPlus la distance entre le point et le résultat de la décision optimale du point de vue de Dieu par rapport à la situation réelle est petite, mieux c'est. l'effet individuel de la stratégie dans l'ensemble de l'espace, mais si elle peut trouver la distance par rapport à la décision optimale. Les avantages sont relativement proches de la zone et si le point optimal peut être prédit avec précision. L'optimisation de la stratégie et la prédiction des effets individuels de la stratégie ont des objectifs différents et il existe des différences évidentes. Comme le montre l'image ci-dessus Comme le montre la figure, l'axe horizontal représente les différentes interventions (traitements), la ligne verte est la fonction réelle du point de vue de Dieu, reflétant les résultats réels d'une certaine intervention, la ligne rouge et la ligne bleue reflètent les résultats des deux prédictions ; modèles. Du point de vue de l'évaluation de la prévision des effets individuels de la stratégie, il est évident que la ligne bleue est meilleure que la ligne rouge. L'écart global de la ligne bleue par rapport à la ligne verte est bien inférieur à l'écart global de la ligne rouge par rapport à la ligne rouge. la ligne verte. Mais du point de vue d'une prise de décision optimale, le résultat optimal de la ligne rouge est plus proche du résultat optimal de la ligne verte du point de vue de Dieu, et l'intervention correspondante est également plus proche, tandis que la ligne bleue est évidemment plus éloignée. Par conséquent, un meilleur modèle de prédiction des effets individuels ne conduit pas nécessairement à une décision optimale ; et dans les scénarios réels, la quantité de données est généralement insuffisante pour optimiser l’ensemble de l’espace, il est préférable d’effectuer l’optimisation uniquement du point de vue des résultats. . Lors de l'optimisation dans une sous-zone, l'effet et l'intensité de l'optimisation sont différents.

Par conséquent, une nouvelle méthode d'optimisation stratégique OOSR est proposée. Le but est de renforcer la prédiction et l'optimisation des zones d'intervention avec de meilleurs résultats, plutôt que d'optimiser dans l'ensemble de l'espace. Par conséquent, lors d’une optimisation, lors d’une pondération axée sur les résultats, plus l’intervention actuelle est proche de la solution optimale donnée qui a été formée, plus l’optimisation sera forte.
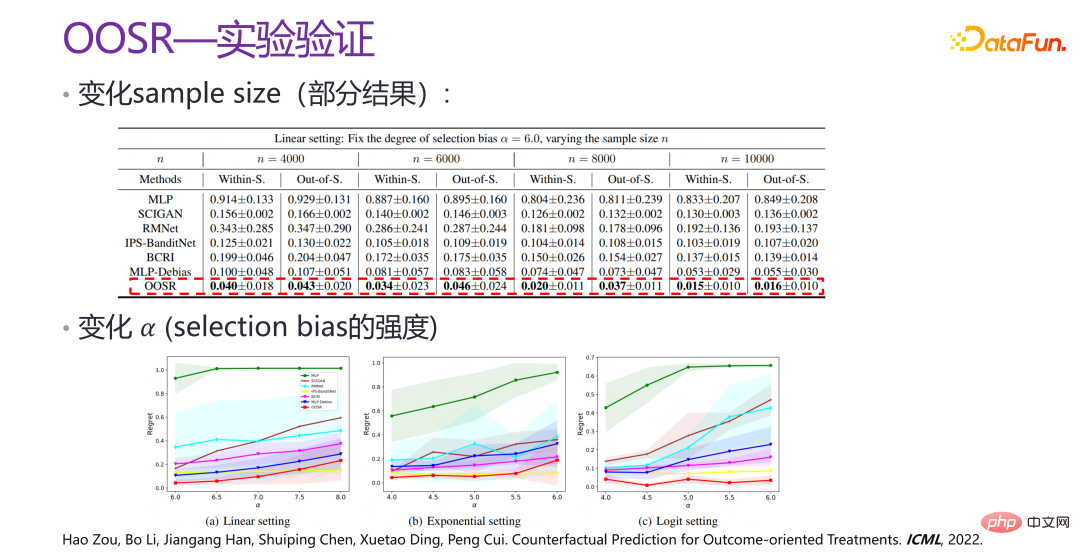
5. Résumé du raisonnement contrefactuel
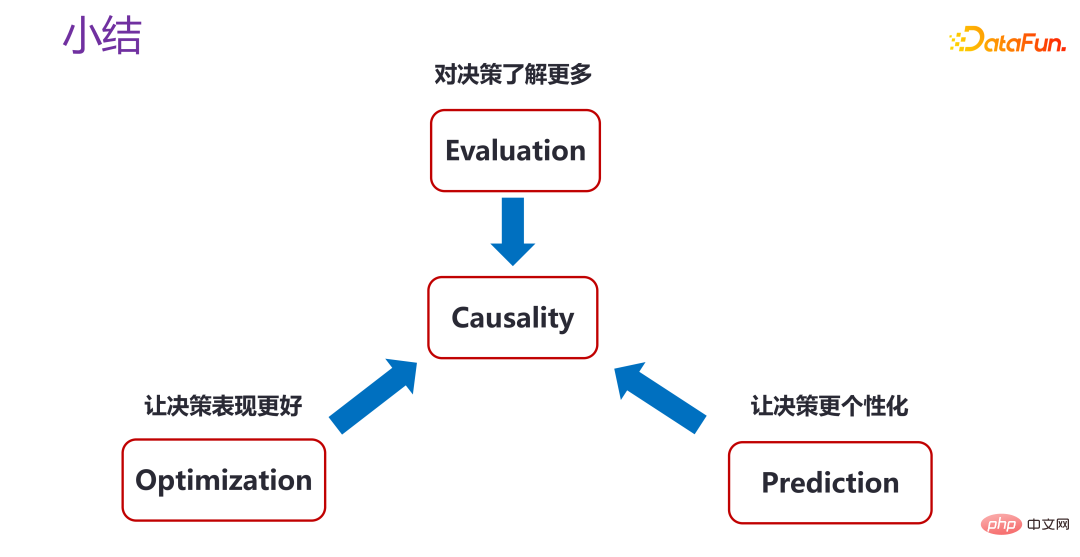
3. Les avantages complexes dans une prise de décision intelligente et fiable



, pensez à celui-ci Des scénarios, tels que les systèmes de recommandation, espèrent que les utilisateurs achèteront ou cliqueront sur des produits ou des informations recommandés, et certaines incitations seront également mises en œuvre, telles que des réductions de prix ou des commentaires sur des enveloppes rouges, etc. Il existe de nombreuses stratégies commerciales similaires, bien que les ventes ont augmenté à court terme, l'effet d'amélioration est très significatif, mais à long terme il n'y a pas de changement très significatif, c'est-à-dire qu'une grande partie de la stimulation commerciale ne transforme pas les gens qui ne veulent pas acheter en gens. qui veut acheter, mais la demande totale par mois est de 4 pièces. J'ai acheté les 4 pièces d'un coup lorsque le prix a baissé. Par conséquent, lors de l'optimisation du modèle, nous devons non seulement considérer les avantages à court terme, mais également considérer les avantages à court et à long terme pour optimiser ensemble les stratégies. 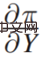


À en juger par l'effet final, comme le montre l'image ci-dessus, il y a une augmentation significative des revenus dans de nombreux scénarios réels. Des articles connexes ont été publiés dans NeurIPS 2022 [5].
4. L'équité prédictive dans une prise de décision intelligente et fiable
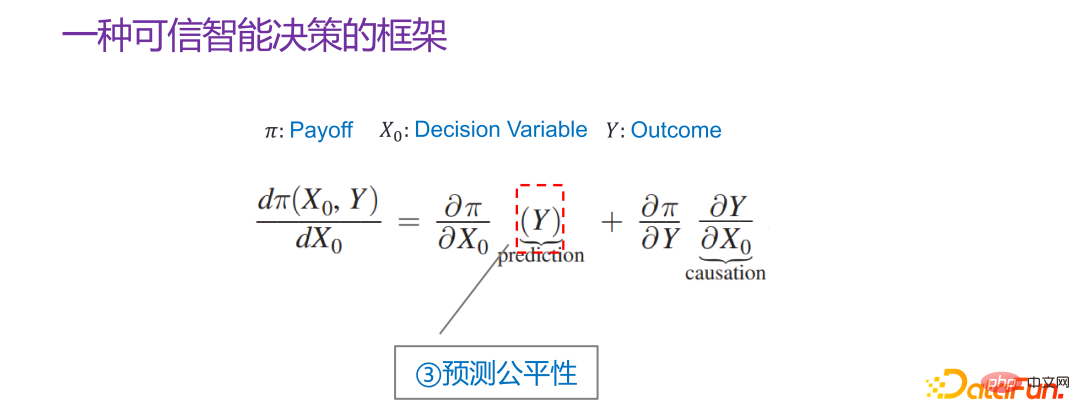

Si la prédiction doit être impliquée dans la prise de décision, en particulier la prise de décision à caractère social , ça doit être L'équité de la prédiction doit être prise en compte.

Concernant l'équité, les méthodes traditionnelles incluent DP et EO, qui exigent que la probabilité d'acceptation des hommes et des femmes soit égale, ou que la capacité prédictive des hommes et des femmes soit la même, qui sont relativement indicateurs classiques. Mais DP et EO ne peuvent pas résoudre essentiellement la question de l’équité.
Par exemple, dans le cas des admissions à l'université, théoriquement le taux d'admission des garçons et des filles dans chaque département devrait être le même, mais en fait on constatera que le taux d'admission des filles est généralement inférieur. en fait, c'est une sorte de paradoxe de la théorie de Simpson. L'admission à l'université est essentiellement un cas équitable, mais lorsqu'elle est détectée par l'indicateur du DP, elle sera considérée comme injuste. En fait, le DP n'est pas un indicateur d'équité très parfait.


EO L'essence du modèle est en effet que le genre participe à la prise de décision, mais dans un scénario injuste, s'il existe un prédicteur parfait pour les hommes et les femmes, on considère que c'est juste. Cela montre que le taux de discrimination de l’EO est insuffisant.

En 2020, le concept d'équité conditionnelle a été proposé. L'équité conditionnelle ne garantit pas absolument que le résultat final soit indépendant des attributs sensibles, mais qu'étant donné certaines variables d'équité, le résultat final soit considéré comme équitable s'il est indépendant des attributs sensibles. Par exemple, la sélection majeure est juste et constitue une variable équitable, car elle peut être décidée par l’initiative subjective des étudiants, et il n’y a pas de problème d’équité.
Faire cela apporte de nombreux avantages. Du point de vue de la prédiction, il existe en réalité un compromis entre équité et prédiction. Autrement dit, plus l’exigence d’équité est forte, moins il y a de variables prédictives disponibles. Par exemple, dans le cadre de l’EO, tant qu’une variable est liée au sexe et à la prise de décision en matière de résultats, elle ne peut pas être utilisée. Si elle est utilisée, de nombreuses variables auront en fait une efficacité de prédiction très élevée, mais ne pourront pas faire de prédictions. Cependant, dans des conditions d'équité conditionnelle, étant donné une variable d'équité, l'efficacité de la prédiction peut être garantie d'être disponible, qu'elle soit sur la liaison ou non.
Dans ce cadre, le modèle d'algorithme DCFR est conçu et proposé, comme le montrent les trois figures suivantes.



La figure ci-dessous montre la vérification expérimentale de l'algorithme DCFR. Dans l'ensemble, l'algorithme DCFR permet d'obtenir un meilleur compromis entre prédiction et équité. Du point de vue de l'optimalité de Pareto, la courbe supérieure gauche est en fait meilleure. Des articles connexes ont été publiés dans KDD 2020 [6]. 5. Supervisabilité dans une prise de décision intelligente et fiable Décision
Enfin, il existe des décisions réglementaires dans une prise de décision intelligente et fiable. 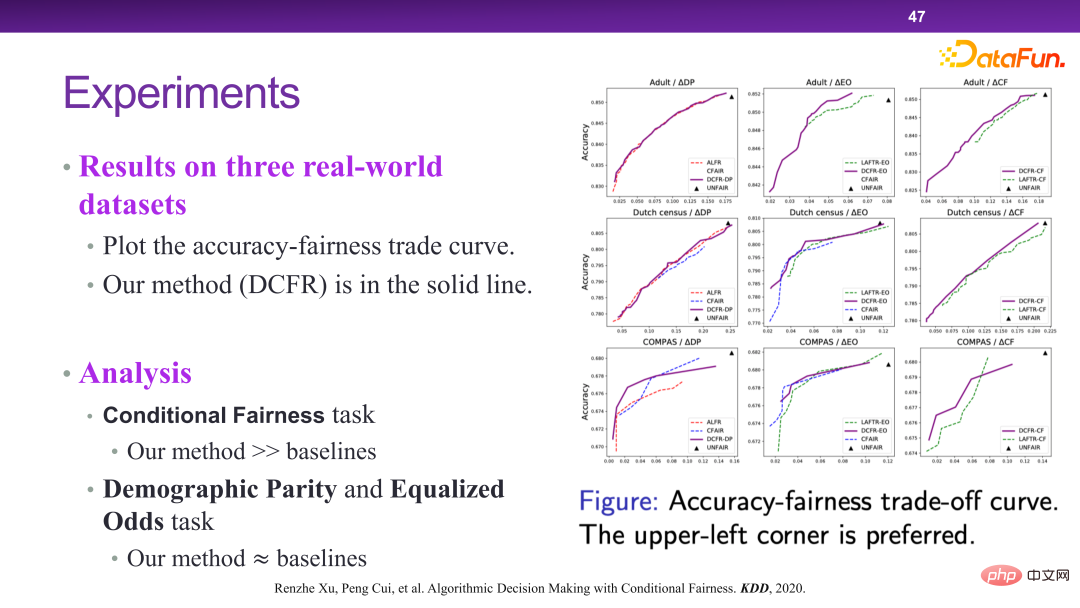
# 🎜 🎜#
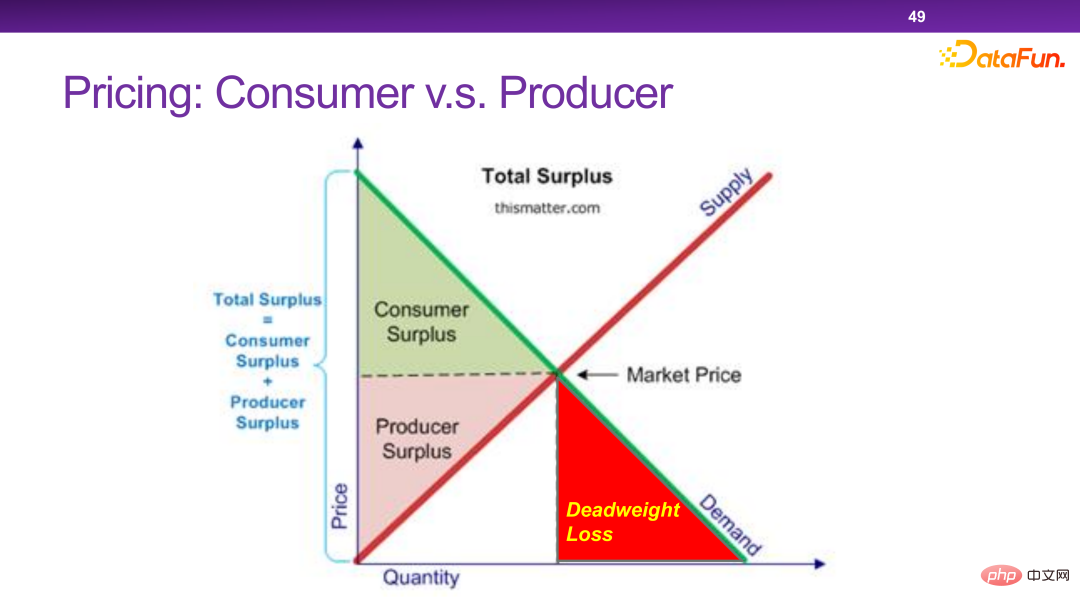
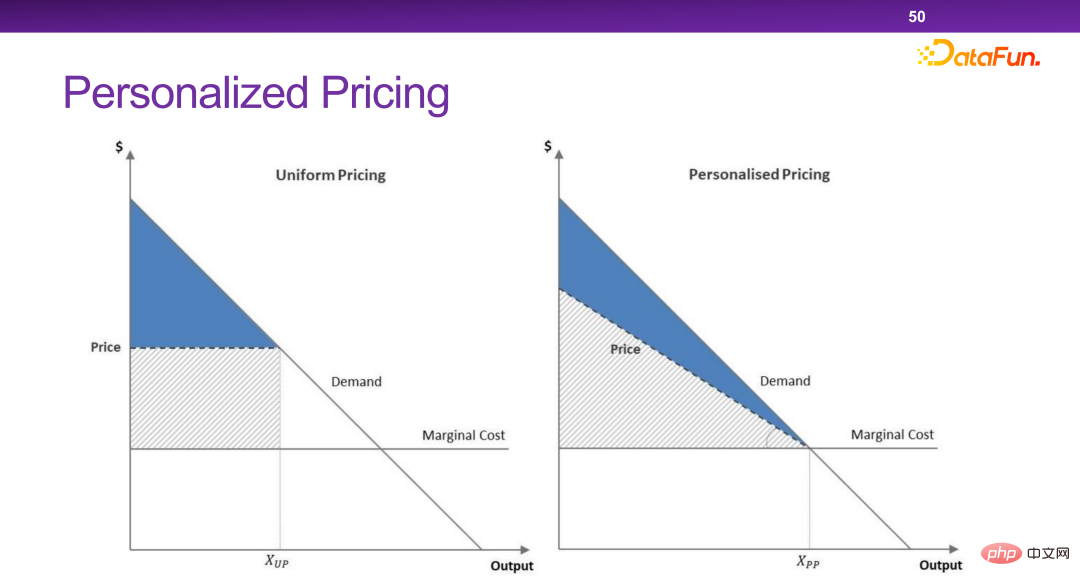
Les plateformes d'aujourd'hui disposent de nombreux mécanismes de tarification personnalisés. Essentiellement, une tarification personnalisée peut maximiser l’efficacité totale et le surplus total de la société. Mais dans certains cas extrêmes, les commerçants retireront tout le surplus sans laisser aucun surplus aux utilisateurs. C’est quelque chose que nous ne voulons pas voir. 
# 🎜 🎜#
Globalement, il est nécessaire de concevoir une stratégie qui permette aux entreprises de transférer une partie de ce qui peut être considéré comme de la richesse sans que le surplus social total soit grandement affecté. consommateurs.

# 🎜 🎜#
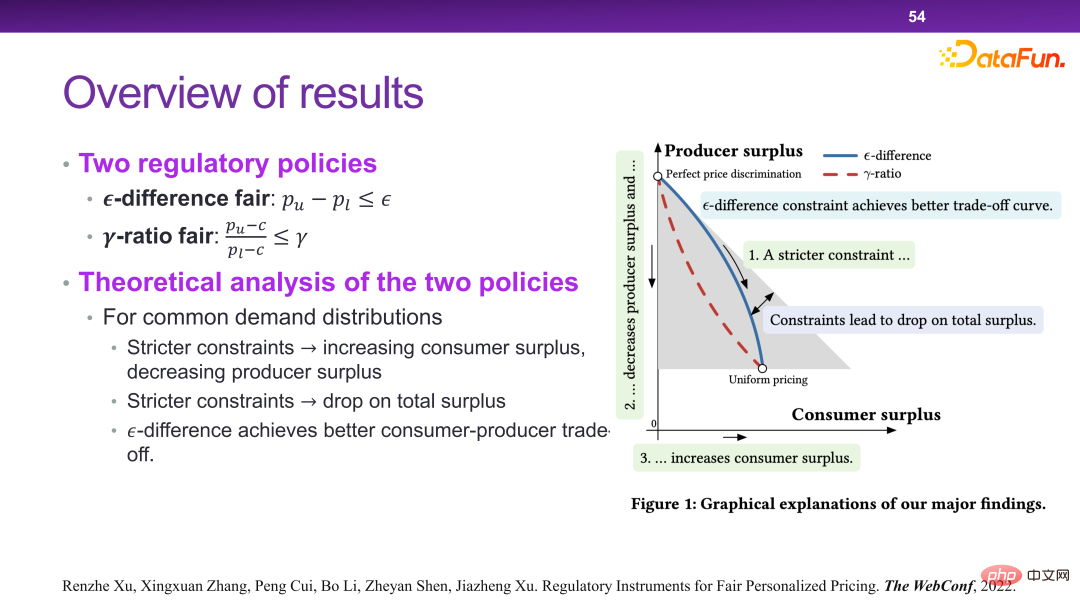
Enfin, une méthode de contrôle a été conçue pour résoudre ce problème, comme le montre la figure ci-dessous. C'est par exemple que pour un même produit, le prix maximum et le prix minimum ne peuvent pas dépasser un, ou ne peuvent pas dépasser un certain rapport. Il peut être théoriquement prouvé que des règles ainsi conçues peuvent atteindre les objectifs d’optimisation mentionnés ci-dessus.

# 🎜 🎜#Dans ce scénario, essentiellement en ajoutant quelques contraintes à la fonction de revenu, un autre niveau de considération doit être pris en compte lors de la prise de décisions. Ainsi, dans le cadre de ce système, certaines stratégies ou outils liés à la supervision peuvent être ajoutés.
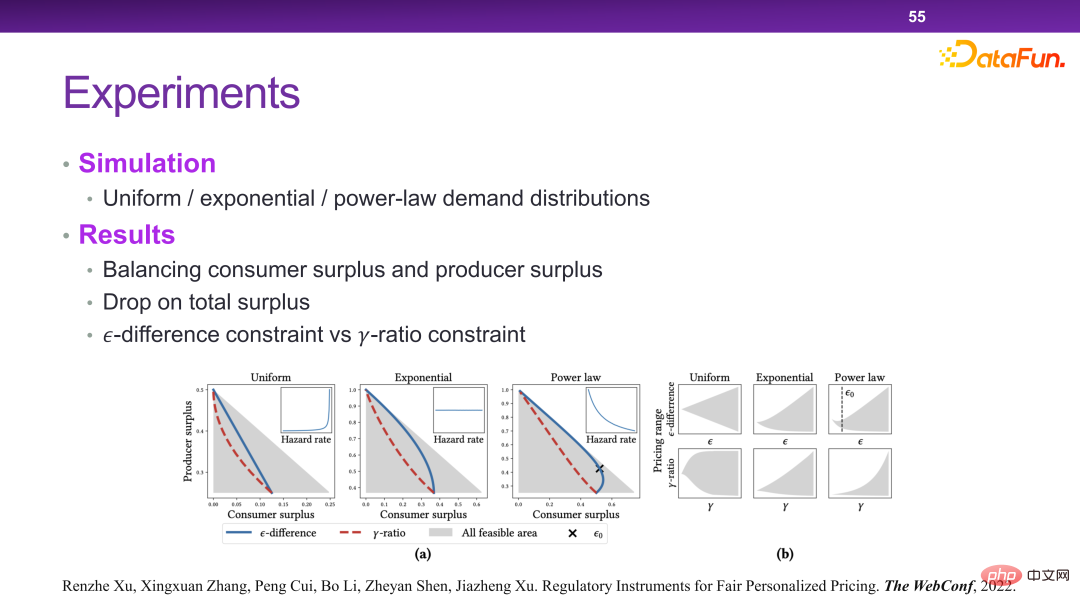
Ce qui précède s'inscrit dans le cadre d'une prise de décision intelligente et fiable , certaines tentatives ont été faites sur divers points uniques du raisonnement contrefactuel, des rendements complexes, de l'équité prédictive et de la prise de décision réglementaire. Dans l’ensemble, la prise de décision est bien plus imaginative que la prévision. Dans le domaine de la prise de décision, de nombreuses questions restent en suspens, étroitement liées à nos vies et à nos entreprises et méritent d’être explorées. Des articles connexes ont été publiés dans WWW 2022 [7]. 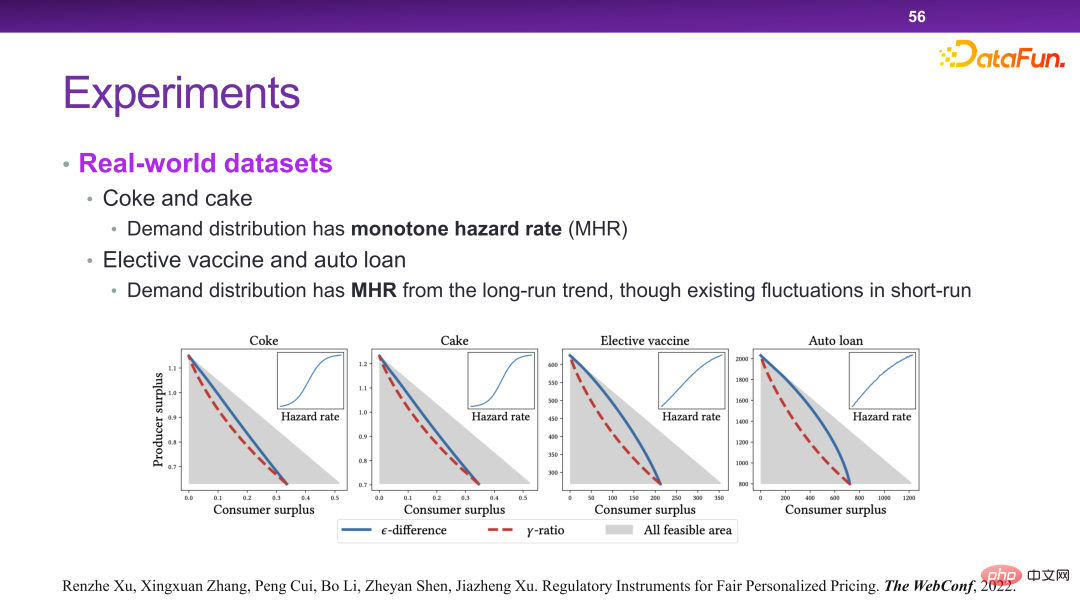
PS : Pour de nombreux détails techniques impliqués dans cet article, vous pouvez vous référer aux articles récents publiés par l'équipe de Cui Peng dans le sens d'une prise de décision intelligente et fiable.
7. Références
[1] Jon Kleinberg, Jens Ludwig, Sendhil Mullainathan, Ziad Obermeyer.
[2] Hao Zou, Kun Kuang, Boqi Chen, Peng Cui, Peixuan Chen. Équilibrage du contexte ciblé pour une évaluation robuste des politiques hors ligne, 2019.
[3] Hao Zou, Peng Cui, Bo Li, Zheyan Shen, Jianxin Ma, Hongxia Yang, Yue He. Prédiction contrefactuelle pour les traitements groupés.
[4] Hao Zou, Bo Li, Jiangang Han, Shuiping Chen, Xuetao Ding, Peng Cui Prédiction contrefactuelle pour les traitements axés sur les résultats ICML, 2022.
[5] Renzhe Xu, Xingxuan Zhang, Bo Li, Yafeng Zhang, Xiaolong Chen, Peng Cui Classement des produits pour la maximisation des revenus avec des achats multiples, 2022.
[6] Renzhe Xu, Peng Cui, Kun Kuang, Bo Li, Linjun Zhou, Zheyan Shen et Wei Cui Prise de décision algorithmique avec équité conditionnelle, 2020.
[7] Renzhe Xu, Xingxuan Zhang, Peng Cui, Bo Li, Zheyan Shen, Jiazheng Xu, Instruments de réglementation pour une tarification personnalisée équitable WWW, 2022.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

