bulleméthode de tri
|
#🎜 🎜 #
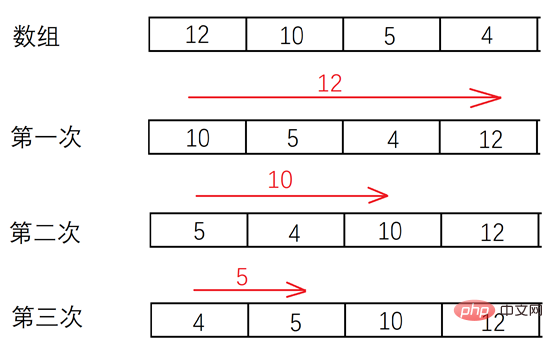
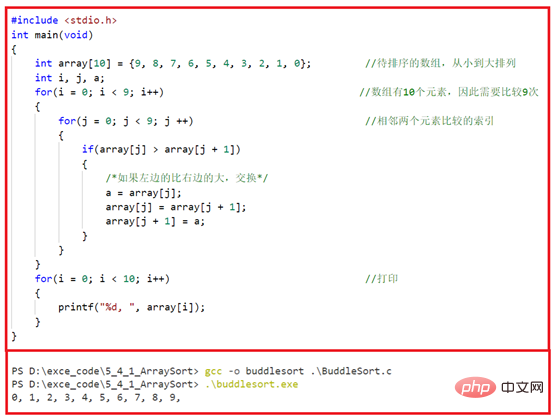
Méthode de tri des bulles L'algorithme des bulles est largement discuté dans les manuels traditionnels en langage C. Il s'agit d'un algorithme de tri relativement stable. Lorsque vous utilisez cet algorithme de tri, vous pouvez penser à sa forme d'implémentation à partir de son nom. Lorsqu'il s'agit de bouillonner, la première chose qui vient à l'esprit est un petit poisson nageant dans l'eau, crachant un chapelet de petites bulles et remontant à la surface de l'eau. En fait, la méthode de tri des bulles est la même que pour faire éclater des bulles. Elle n'en crache qu'une à la fois et les crache les unes après les autres en continu. L'idée centrale de l'algorithme de tri à bulles est de comparer deux nombres adjacents puis d'échanger leurs positions en fonction des exigences de taille. Commençons par le tableau le plus simple de deux éléments et tirons-en des conclusions. Supposons qu'il n'y ait que deux éléments dans un tableau "int array = {8, 0};". Lors du tri, nous n'avons besoin que d'un seul jugement pour savoir quel élément est le plus grand et quel élément est le plus petit. En supposant que nous classions du plus petit au plus grand, le résultat de l'arrangement devrait être "array = {0, 8};". Regardons un tableau avec trois éléments. Supposons qu'il n'y ait que deux éléments dans un tableau "int array = {8, 0, 1};". Ensuite, nous effectuons toujours une comparaison par paire. Dans la première comparaison, nous pouvons conclure que le tableau doit être "array = {0, 1, 8};", et une seule comparaison est nécessaire pour terminer le tri du tableau. Mais si le tableau change la position des éléments, c'est-à-dire "int array = {8, 1, 0};", alors jetons un coup d'oeil à nouveau. La première comparaison par paire d'éléments devient "array = {1, 0, 8} ;", donc lorsque nous rencontrons cette situation extrême, la méthode des bulles ne peut pas terminer le tri avec une seule comparaison, alors une deuxième comparaison doit être effectuée. Enfin, dans la deuxième comparaison, nous pouvons obtenir le résultat "array = {0, 1, 8}; "Regardons le tri du tableau lorsqu'il y a quatre éléments. Cette fois, nous prenons un cas extrême, c'est-à-dire changer un tableau disposé du grand au petit en un tableau disposé du petit au grand. Le tableau est "int array = {9, 8, 1, 0};". Ensuite, à ce moment-là, la première comparaison de deux éléments adjacents peut donner "tableau = {8, 1, 0, 9} ;", et la deuxième comparaison d'éléments adjacents peut donner "tableau = {1, 0, 8, 9} ;", la troisième comparaison par paire peut donner "array = {0, 1, 8, 9};". Sur la base de l'analyse ci-dessus, nous pouvons savoir que si un tableau comporte n éléments qui doivent être triés, le cas extrême de tri devrait être n-1 fois. Le processus de tri spécifique est le suivant.

Le processus de la méthode de tri des bulles
Donc, sur la base de l'analyse ci-dessus, nous pouvons écrire le code comme suit.

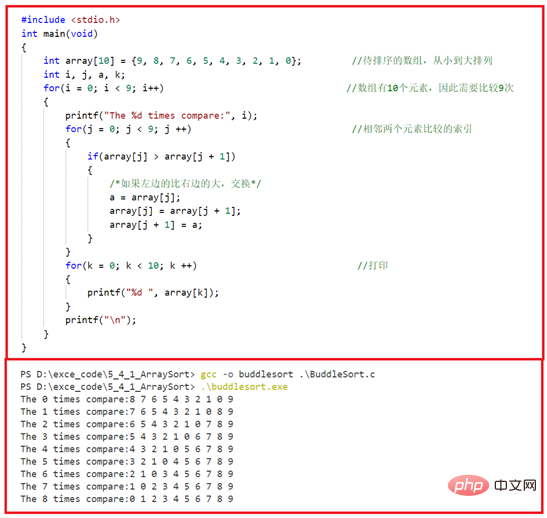
Ensuite, nous modifions le programme pour qu'il imprime la comparaison de deux éléments adjacents à chaque étape, comme le montre la figure 5-4-3. Nous pouvons voir que les éléments plus gros vont lentement « flotter » vers le haut de la séquence par échange (disposés par ordre croissant ou décroissant), tout comme un chapelet de bulles craché par un petit poisson rouge dans l'eau, émergeant lentement de l'eau, d'où le nom "Tri à bulles".

Tri à bulles, impression en une seule étape
Méthode de tri par sélection
Tri par sélection Tri par sélection, communément appelé "tri par balle", bien sûr, ce "tri par balle" est ce que j'ai nommé Son nom, parce qu'il s'agit de la méthode de tri la plus intuitive, explique parfaitement les quatre mots « esthétique de la violence ». Pour comprendre le tri de sélection, imaginez d’abord comment l’enseignant organise les équipes dans un cours d’éducation physique à l’école primaire. Tout d'abord, sélectionnez au hasard parmi les enfants un élève que l'enseignant considère comme le plus petit et laissez-le être le leader. Ensuite, comparez les autres élèves à son tour. S'il est plus grand, il sera placé derrière lui. il sera placé devant. Puis inspectez visuellement le deuxième, et ainsi de suite. Bien entendu, le paragraphe ci-dessus décrit les pensées intérieures du professeur d’éducation physique. Lorsque nous trions le tableau, nous pouvons également utiliser cette méthode. Nous pouvons d'abord désigner une avant-garde. Supposons que nous voulions organiser du petit au grand, alors nous supposons d'abord que le premier élément est le plus petit élément du tableau, puis le comparons respectivement avec les éléments restants s'il s'avère plus petit. que lui, puis échangez-le avec cet élément. De cette façon, il vous suffit de parcourir tout le tableau et de placer le plus petit élément à la position du premier élément. Comme indiqué ci-dessous.

Le tri par sélection effectue une comparaison transversale
Dans l'image ci-dessus, grâce à la première comparaison transversale, nous avons disposé les plus petits éléments à l'extrémité la plus à gauche du tableau, et ce que nous devons faire ensuite n'en est qu'un pass Comparez les 9 éléments restants pour trouver la valeur minimale, puis placez-la à droite de 0, et ainsi de suite. Enfin, nous pouvons écrire le programme de tri par sélection comme le montre la figure ci-dessous.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!