Maison >Périphériques technologiques >IA >Résumé comparatif de cinq modèles d'apprentissage profond pour la prévision de séries chronologiques
Résumé comparatif de cinq modèles d'apprentissage profond pour la prévision de séries chronologiques
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-05-05 17:16:072226parcourir
Makridakis Les séries M-Competitions (appelées respectivement M4 et M5) ont eu lieu respectivement en 2018 et 2020 (M6 a également eu lieu cette année). Pour ceux qui ne le savent pas, le concours m-series peut être considéré comme un résumé de l’état actuel de l’écosystème des séries chronologiques, fournissant des preuves empiriques et objectives de la théorie et de la pratique actuelles de la prévision.
Les résultats du M4 2018 ont montré que les méthodes pures « ML » surpassaient largement les méthodes statistiques traditionnelles, ce qui était inattendu à l'époque. En M5[1] deux ans plus tard, le score le plus élevé était avec les seules méthodes « ML ». Et tous les 50 premiers sont essentiellement basés sur le ML (principalement des modèles d'arbres). Ce concours a vu les débuts de LightGBM (pour la prévision de séries chronologiques) ainsi que de Deepar [2] et N-Beats d'Amazon [3]. Le modèle N-Beats est sorti en 2020 et est 3% meilleur que le gagnant du concours M4 !
Le récent concours de prévision de la pression respiratoire a démontré l'importance d'utiliser des méthodes d'apprentissage profond pour relever les défis des séries chronologiques en temps réel. Le but du concours est de prédire la séquence temporelle des pressions au sein d'un poumon mécanique. Chaque instance de formation est sa propre série chronologique, la tâche est donc un problème de séries chronologiques multiples. L'équipe gagnante a soumis une architecture profonde multicouche comprenant un réseau LSTM et un bloc Transformer.
Au cours des dernières années, de nombreuses architectures célèbres ont été publiées, telles que MQRNN et DSSM. Tous ces modèles apportent de nombreuses nouveautés dans le domaine de la prévision de séries chronologiques grâce au deep learning. En plus de gagner des concours Kaggle, cela nous a également apporté plus de progrès tels que :
- Polyvalence : la possibilité d'utiliser le modèle pour différentes tâches.
- MLOP : La possibilité d'utiliser des modèles en production.
- Interprétabilité et interprétabilité : Les modèles de boîtes noires ne sont pas si populaires.
Cet article traite de 5 architectures d'apprentissage profond spécialisées dans la prédiction de séries chronologiques. L'article est :
- N-BEATS(ElementAI)# 🎜. 🎜# DeepAR(Amazon)
- Spacetimeformer[4]
- Temporal Fusion Transformer ou TFT(Google) [5]
- TSFormer (MAE en Time Series)[7]
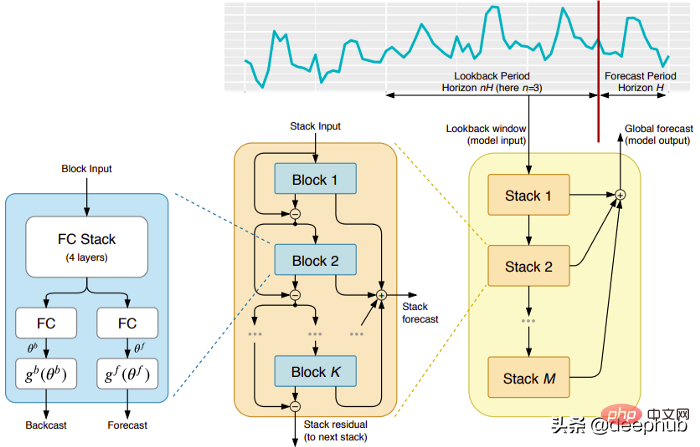
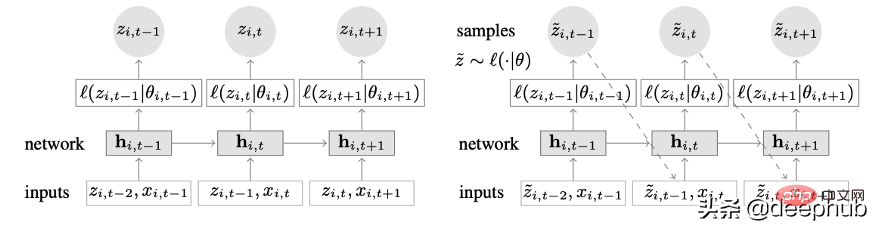
Voici les principaux avantages de ce modèle :
DeepAR fonctionne très bien sur plusieurs séries temporelles : un modèle global est construit en utilisant plusieurs séries temporelles avec des distributions légèrement différentes. Applicable également à de nombreux scénarios réels. Par exemple, une compagnie d’électricité peut souhaiter lancer un service de prévision de puissance pour chaque client, chacun ayant des modes de consommation différents (ce qui signifie des distributions différentes).
En plus des données historiques, DeepAR permet également d'utiliser des séries temporelles futures connues (une caractéristique des modèles autorégressifs) et des attributs statiques supplémentaires. Dans le scénario de prévision de la demande d'électricité mentionné précédemment, une variable temporelle supplémentaire pourrait être le mois (sous forme d'entier avec une valeur comprise entre 1 et 12). En supposant que chaque client soit associé à un capteur qui mesure la consommation d'énergie, les variables statiques supplémentaires seraient quelque chose comme sensor_id ou customer_id.
Si vous êtes habitué à utiliser des architectures de réseaux neuronaux telles que les MLP et les RNN pour la prévision de séries chronologiques, une étape clé du prétraitement consiste à mettre à l'échelle la série chronologique à l'aide de techniques de normalisation ou de normalisation. Cela ne nécessite pas d'opération manuelle dans DeepAR, car le modèle sous-jacent met à l'échelle l'entrée autorégressive z pour chaque série temporelle i par un facteur d'échelle v_i, qui est la moyenne de cette série temporelle. Plus précisément, l'équation du facteur d'échelle utilisée dans le benchmark de l'article est la suivante :

Mais en pratique, si la taille de la série temporelle cible varie considérablement, il est toujours nécessaire d'appliquer votre propre mise à l'échelle lors du prétraitement. Par exemple, dans un scénario de prévision de la demande énergétique, l’ensemble de données peut contenir des clients d’électricité à moyenne tension (tels que de petites usines, consommant de l’électricité en mégawatts) et des clients à basse tension (tels que des ménages, consommant de l’électricité en unités de kilowatts).
DeepAR fait des prédictions probabilistes au lieu de générer directement des valeurs futures. Ceci est réalisé sous forme d'un échantillon de Monte Carlo. Ces prédictions sont utilisées pour calculer des prédictions quantiles à l'aide de la fonction de perte quantile. Pour ceux qui ne connaissent pas ce type de perte, la perte quantile est utilisée pour calculer non seulement une estimation, mais aussi un intervalle de prédiction autour de cette valeur.
Spacetimeformer
La dépendance temporelle est la plus importante dans les séries chronologiques univariées. Mais dans plusieurs scénarios de séries chronologiques, les choses ne sont pas si simples. Par exemple, supposons que nous ayons une tâche de prévisions météorologiques et que nous souhaitions prédire la température de cinq villes. Supposons que ces villes appartiennent à un pays. Compte tenu de ce que nous avons vu jusqu’à présent, nous pouvons utiliser DeepAR et modéliser chaque ville comme une covariable statique externe.
En d’autres termes, le modèle prendra en compte à la fois les relations temporelles et spatiales. C'est l'idée centrale de Spacetimeformer : utiliser un modèle pour exploiter les relations spatiales entre ces villes/lieux, apprenant ainsi des dépendances supplémentaires utiles car le modèle prendra en compte à la fois les relations temporelles et spatiales.
Étude approfondie des séquences spatio-temporelles
Comme son nom l'indique, ce modèle utilise en interne une structure basée sur des transformateurs. Lors de l'utilisation de modèles basés sur des transformateurs pour la prédiction de séries chronologiques, une technique populaire pour produire des intégrations sensibles au temps consiste à transmettre l'entrée via une couche d'intégration Time2Vec [6] (pour les tâches PNL, des vecteurs de codage positionnels sont utilisés à la place de Time2Vec). Bien que cette technique fonctionne très bien pour les séries temporelles univariées, elle n'a pas de sens pour les entrées temporelles multivariées. Il se peut que dans la modélisation du langage, chaque mot d'une phrase soit représenté par un incorporation, et qu'un mot soit essentiellement une partie du vocabulaire, alors que les séries temporelles ne sont pas si simples.
Dans les séries chronologiques multivariées, à un pas de temps t donné, l'entrée se présente sous la forme x_1,t, x2,t, x_m,t où x_i,t est la valeur de la caractéristique i et m est le nombre total de caractéristiques /séquences. Si nous transmettons l'entrée via une couche Time2Vec, un vecteur d'intégration temporel sera produit. Que représente réellement cette intégration ? La réponse est qu’elle représentera l’ensemble de la collection d’entrées comme une seule entité (jeton). Ainsi, le modèle n'apprendra que la dynamique temporelle entre les pas de temps, mais manquera les relations spatiales entre les caractéristiques/variables.
Spacetimeformer résout ce problème en aplatissant l'entrée dans un grand vecteur appelé séquence espace-temps. Si l'entrée contient N variables, organisées en T pas de temps, la séquence spatio-temporelle résultante aura l'étiquette (NxT). La figure 3 ci-dessous le montre mieux :
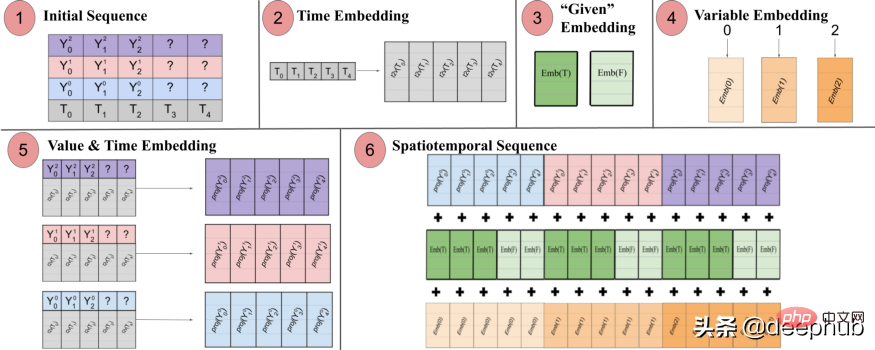
Le document indique : "(1) Format d'entrée multivarié contenant des informations temporelles. L'entrée du décodeur manque de valeurs ("?") et est définie sur zéro lors des prédictions. (2) La série chronologique passe par une couche Time2Vec pour générer une représentation de la périodicité Incorporation de fréquence du modèle d'entrée. (3) L'intégration binaire indique si la valeur est donnée comme contexte ou doit être prédite (4) Mappage de l'indice entier de chaque série temporelle à une représentation « spatiale ». avec une intégration de table de recherche. 5) Utiliser une couche de rétroaction pour projeter l'intégration Time2Vec et les valeurs variables de chaque série chronologique (6) La somme des valeurs et du temps, des variables et des intégrations données entraîne un allongement du MSA entre le temps et la variable. espace. Séquence en entrée.
En d'autres termes, la séquence finale code un intégration unifiée qui contient des informations temporelles, spatiales et contextuelles. Cependant, un inconvénient de cette méthode est que la séquence peut devenir très longue, ce qui entraîne une croissance secondaire des ressources. En effet, selon le mécanisme d'attention, chaque jeton est comparé à un autre. L'auteur utilise une architecture plus efficace appelée mécanisme d'attention Performer, qui convient aux séquences plus grandes.
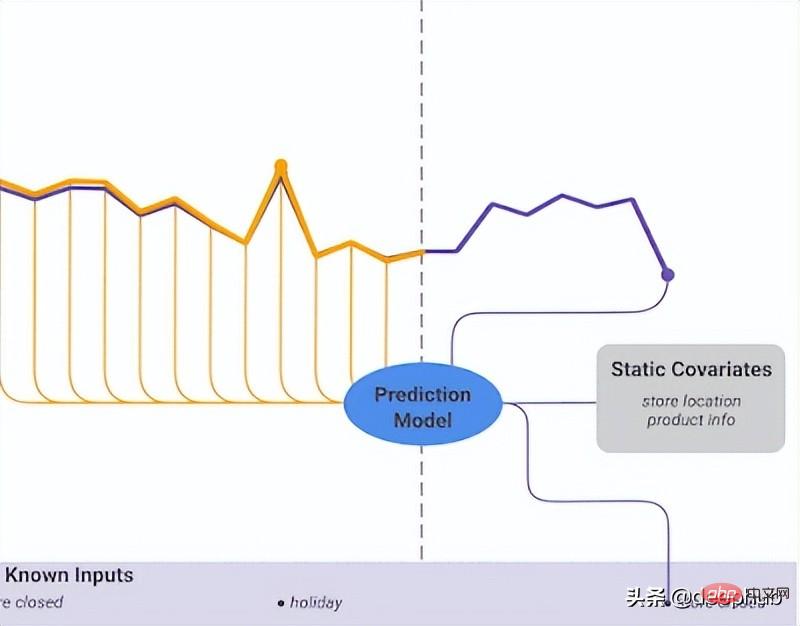
Temporal Fusion Transformer (TFT) est une série temporelle basée sur Transformer. Le modèle de prédiction publié par Google est plus polyvalent que les modèles précédents. L'architecture de haut niveau de TFT est illustrée dans la figure 4. :Comme les modèles mentionnés précédemment, TFT prend en charge la création de modèles sur plusieurs séries temporelles hétérogènes TFT en prend en charge trois. types de fonctionnalités : i) Données variables dans le temps avec entrées futures connues ii) Données variables dans le temps connues jusqu'à présent iii) Variables catégorielles/statiques, également connues sous le nom de fonctionnalités invariantes dans le temps. Par conséquent, TFT est plus polyvalent que les modèles précédents. Dans le scénario de prévision de la demande de puissance mentionné précédemment, nous souhaitons utiliser les niveaux d'humidité comme fonctionnalité variable dans le temps, ce qui n'était connu que jusqu'à présent. Cela n'est possible que dans TFT, mais pas dans DeepAR.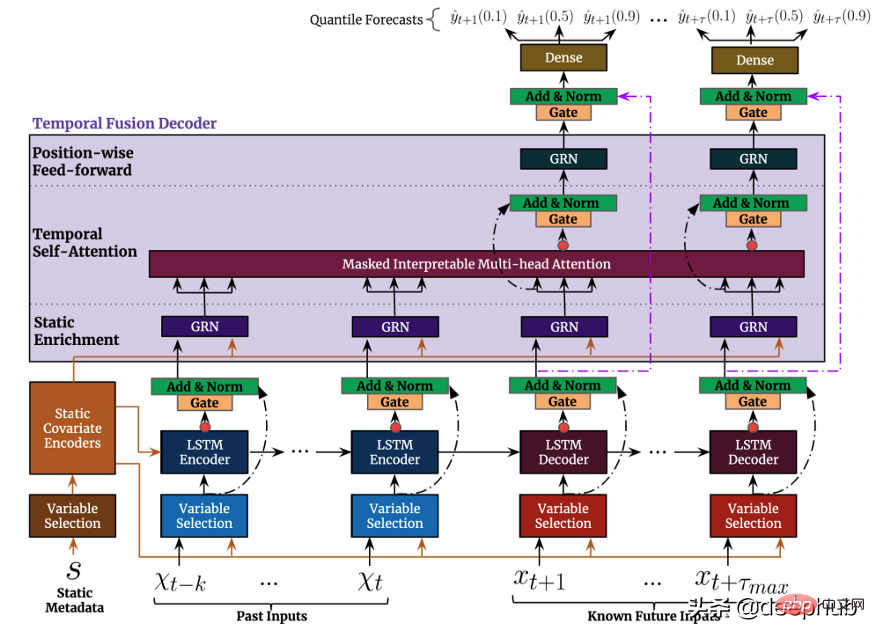 La figure 5 montre un exemple de cette méthode. pour utiliser toutes ces fonctionnalités :
La figure 5 montre un exemple de cette méthode. pour utiliser toutes ces fonctionnalités :
 Cela conduit au dernier modèle que nous souhaitons introduire, TSFormer. Ce modèle considère deux perspectives. Nous le divisons en quatre parties de l'entrée à la sortie et fournissons le code d'implémentation Python (officiellement également fourni), ce modèle vient de sortir, c'est pourquoi nous nous y concentrons ici.
Cela conduit au dernier modèle que nous souhaitons introduire, TSFormer. Ce modèle considère deux perspectives. Nous le divisons en quatre parties de l'entrée à la sortie et fournissons le code d'implémentation Python (officiellement également fourni), ce modèle vient de sortir, c'est pourquoi nous nous y concentrons ici.
TSFormer
Il s'agit d'un modèle de pré-entraînement de séries chronologiques non supervisé basé sur Transformer (TSFormer), qui utilise la stratégie de formation dans MAE et est capable de capturer de très longues dépendances dans les données.
PNL et séries chronologiques :
Dans une certaine mesure, les informations PNL et les données de séries chronologiques sont les mêmes. Ce sont à la fois des données séquentielles et sensibles à la localité, c'est-à-dire par rapport à son point de données suivant/précédent. Mais il existe encore quelques différences, et il y a deux différences que nous devrions prendre en compte lors de l'élaboration de notre modèle pré-entraîné, tout comme nous le faisons dans les tâches de PNL :
La densité des données de séries chronologiques est bien inférieure à celle des données en langage naturel.Nous avons besoin de données de séries chronologiques plus longues que les données PNL
Introduction à TSFormer
TSFormer est fondamentalement similaire à l'architecture principale de MAE. Les données passent par un encodeur puis un décodeur. Le but final est de reconstruire les éléments manquants (. artificielles) masquées).
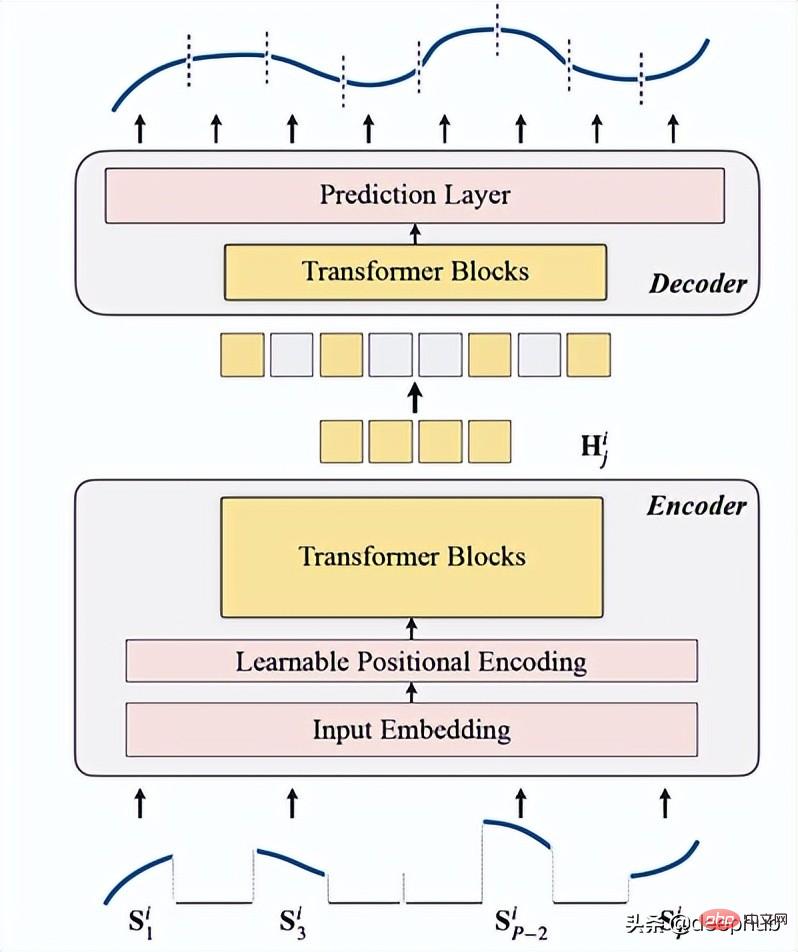
Nous le résumons dans les 4 points suivants :
1. Le masquage
est utilisé comme première étape avant que les données n'entrent dans l'encodeur. La séquence d'entrée (Sᶦ) a été distribuée en P tranches, dont la longueur est L. Par conséquent, la longueur de la fenêtre glissante utilisée pour prédire le prochain pas de temps est P XL.

Le taux de masquage est de 75 % (cela semble très élevé, probablement parce qu'il utilise les mêmes paramètres que MAE) ; ce que nous voulons effectuer est une tâche auto-supervisée, donc moins il y a de données, plus le calcul de l'encodeur est rapide ; vitesse.
La principale raison de cette opération (masquage des segments de séquence d'entrée) est la suivante :
- les segments (patch) sont meilleurs que les points individuels.
- Cela simplifie l'utilisation des modèles en aval (STGNN prend les segments unitaires en entrée)
- peut factoriser la taille d'entrée de l'encodeur.
class Patch(nn.Module):<br>def __init__(self, patch_size, input_channel, output_channel, spectral=True):<br>super().__init__()<br>self.output_channel = output_channel<br>self.P = patch_size<br>self.input_channel = input_channel<br>self.output_channel = output_channel<br>self.spectral = spectral<br>if spectral:<br>self.emb_layer = nn.Linear(int(patch_size/2+1)*2, output_channel)<br>else:<br>self.input_embedding = nn.Conv2d(input_channel, output_channel, kernel_size=(self.P, 1), stride=(self.P, 1))<br>def forward(self, input):<br>B, N, C, L = input.shape<br>if self.spectral:<br>spec_feat_ = torch.fft.rfft(input.unfold(-1, self.P, self.P), dim=-1)<br>real = spec_feat_.real<br>imag = spec_feat_.imag<br>spec_feat = torch.cat([real, imag], dim=-1).squeeze(2)<br>output = self.emb_layer(spec_feat).transpose(-1, -2)<br>else:<br>input = input.unsqueeze(-1) # B, N, C, L, 1<br>input = input.reshape(B*N, C, L, 1) # B*N, C, L, 1<br>output = self.input_embedding(input) # B*N, d, L/P, 1<br>output = output.squeeze(-1).view(B, N, self.output_channel, -1)<br>assert output.shape[-1] == L / self.P<br>return output
Voici la fonction qui génère le masquage :
class MaskGenerator(nn.Module):<br>def __init__(self, mask_size, mask_ratio, distribution='uniform', lm=-1):<br>super().__init__()<br>self.mask_size = mask_size<br>self.mask_ratio = mask_ratio<br>self.sort = True<br>self.average_patch = lm<br>self.distribution = distribution<br>if self.distribution == "geom":<br>assert lm != -1<br>assert distribution in ['geom', 'uniform']<br>def uniform_rand(self):<br>mask = list(range(int(self.mask_size)))<br>random.shuffle(mask)<br>mask_len = int(self.mask_size * self.mask_ratio)<br>self.masked_tokens = mask[:mask_len]<br>self.unmasked_tokens = mask[mask_len:]<br>if self.sort:<br>self.masked_tokens = sorted(self.masked_tokens)<br>self.unmasked_tokens = sorted(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def geometric_rand(self):<br>mask = geom_noise_mask_single(self.mask_size, lm=self.average_patch, masking_ratio=self.mask_ratio) # 1: masked, 0:unmasked<br>self.masked_tokens = np.where(mask)[0].tolist()<br>self.unmasked_tokens = np.where(~mask)[0].tolist()<br># assert len(self.masked_tokens) > len(self.unmasked_tokens)<br>return self.unmasked_tokens, self.masked_tokens<br>def forward(self):<br>if self.distribution == 'geom':<br>self.unmasked_tokens, self.masked_tokens = self.geometric_rand()<br>elif self.distribution == 'uniform':<br>self.unmasked_tokens, self.masked_tokens = self.uniform_rand()<br>else:<br>raise Exception("ERROR")<br>return self.unmasked_tokens, self.masked_tokens
2 Encoding
comprend l'intégration d'entrée, l'encodage de position et le bloc Transformer. L'encodeur ne peut être exécuté que sur des patchs non masqués (c'est aussi la méthode MAE).
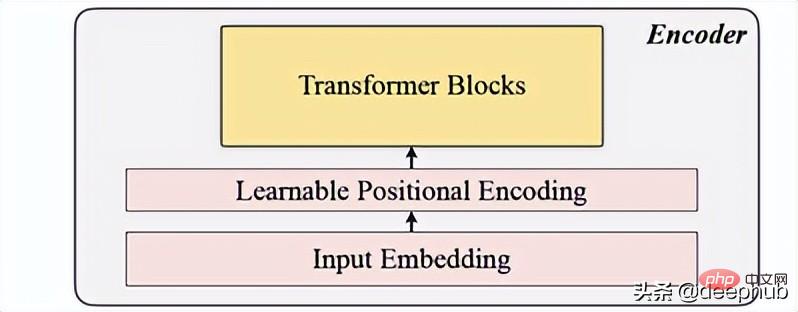
Input embedding
Utilise la projection linéaire pour obtenir l'incorporation d'entrée, qui convertit l'espace non masqué en un espace latent. Sa formule est visible ci-dessous :
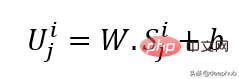
W et B sont les paramètres apprenables et U est le vecteur d'entrée du modèle en dimension.
Encodage positionnel
Une simple couche d'encodage positionnel est utilisée pour ajouter de nouvelles informations séquentielles. Ajout du mot « apprenable », qui permet d'afficher de meilleures performances que sinus. Par conséquent, les intégrations de localisation apprenables montrent de bons résultats pour les séries chronologiques.
class LearnableTemporalPositionalEncoding(nn.Module):<br>def __init__(self, d_model, dropout=0.1, max_len: int = 1000):<br>super().__init__()<br>self.dropout = nn.Dropout(p=dropout)<br>self.pe = nn.Parameter(torch.empty(max_len, d_model), requires_grad=True)<br>nn.init.uniform_(self.pe, -0.02, 0.02)<br><br>def forward(self, X, index):<br>if index is None:<br>pe = self.pe[:X.size(1), :].unsqueeze(0)<br>else:<br>pe = self.pe[index].unsqueeze(0)<br>X = X + pe<br>X = self.dropout(X)<br>return X<br>class PositionalEncoding(nn.Module):<br>def __init__(self, hidden_dim, dropout=0.1):<br>super().__init__()<br>self.tem_pe = LearnableTemporalPositionalEncoding(hidden_dim, dropout)<br>def forward(self, input, index=None, abs_idx=None):<br>B, N, L_P, d = input.shape<br># temporal embedding<br>input = self.tem_pe(input.view(B*N, L_P, d), index=index)<br>input = input.view(B, N, L_P, d)<br># absolute positional embedding<br>return input
Bloc Transformer
Le papier utilise 4 couches de Transformers, ce qui est un nombre inférieur à celui qui est courant dans les tâches de vision par ordinateur et de traitement du langage naturel. Le transformateur utilisé ici est la structure la plus basique mentionnée dans l'article original, comme le montre la figure 4 ci-dessous :
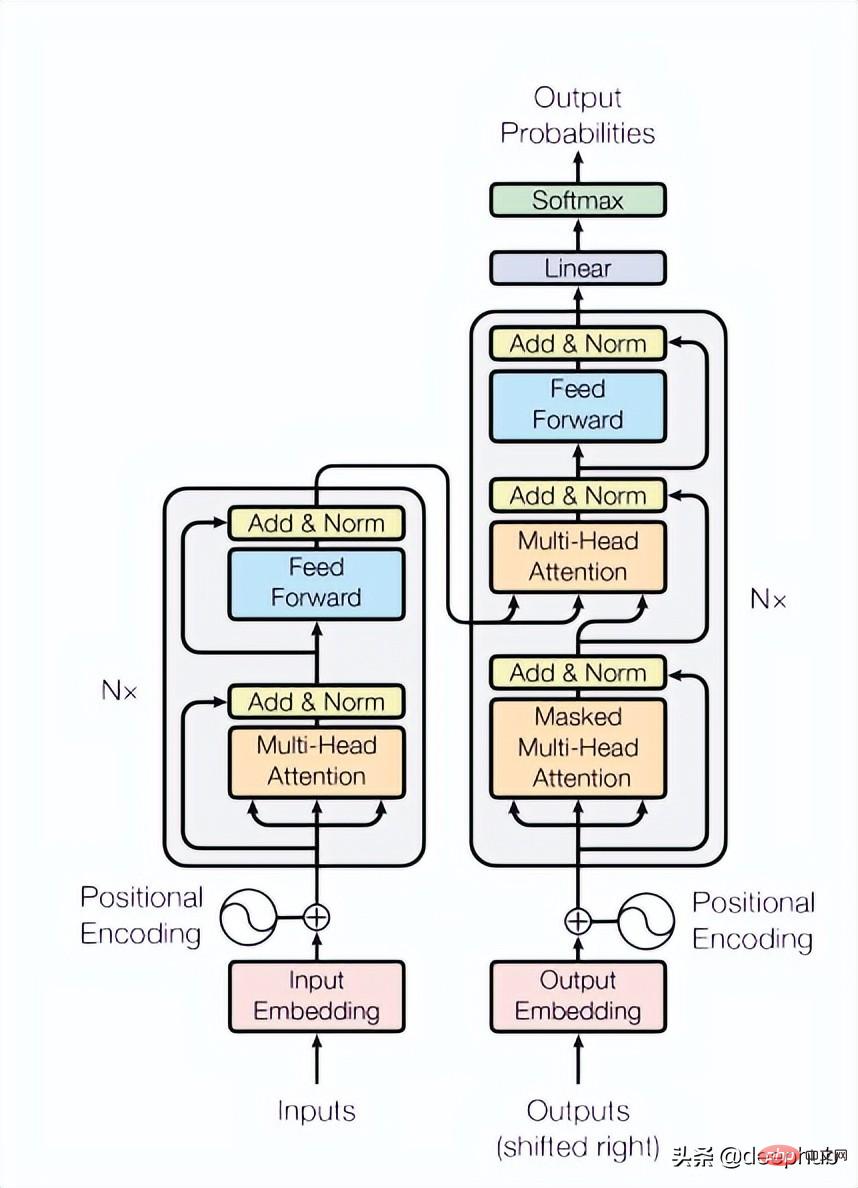
class TransformerLayers(nn.Module):<br>def __init__(self, hidden_dim, nlayers, num_heads=4, dropout=0.1):<br>super().__init__()<br>self.d_model = hidden_dim<br>encoder_layers = TransformerEncoderLayer(hidden_dim, num_heads, hidden_dim*4, dropout)<br>self.transformer_encoder = TransformerEncoder(encoder_layers, nlayers)<br>def forward(self, src):<br>B, N, L, D = src.shape<br>src = src * math.sqrt(self.d_model)<br>src = src.view(B*N, L, D)<br>src = src.transpose(0, 1)<br>output = self.transformer_encoder(src, mask=None)<br>output = output.transpose(0, 1).view(B, N, L, D)<br>return output
3. Décodage
Le décodeur comprend une série de blocs Transformer. Il s'applique à tous les patchs (en revanche, MAE n'a pas d'intégration de position, car ses patchs ont déjà des informations de position), et le nombre de couches n'est qu'un, puis utilise un simple MLP, qui rend la longueur de sortie égale à chaque patch. longueur.
4. Cible de reconstruction

Calculez le patch de masquage pour chaque point de données (i) et sélectionnez mae (Mean-Absolute-Error) comme fonction de perte de la séquence principale et de la séquence reconstruite.

Voici l'architecture globale
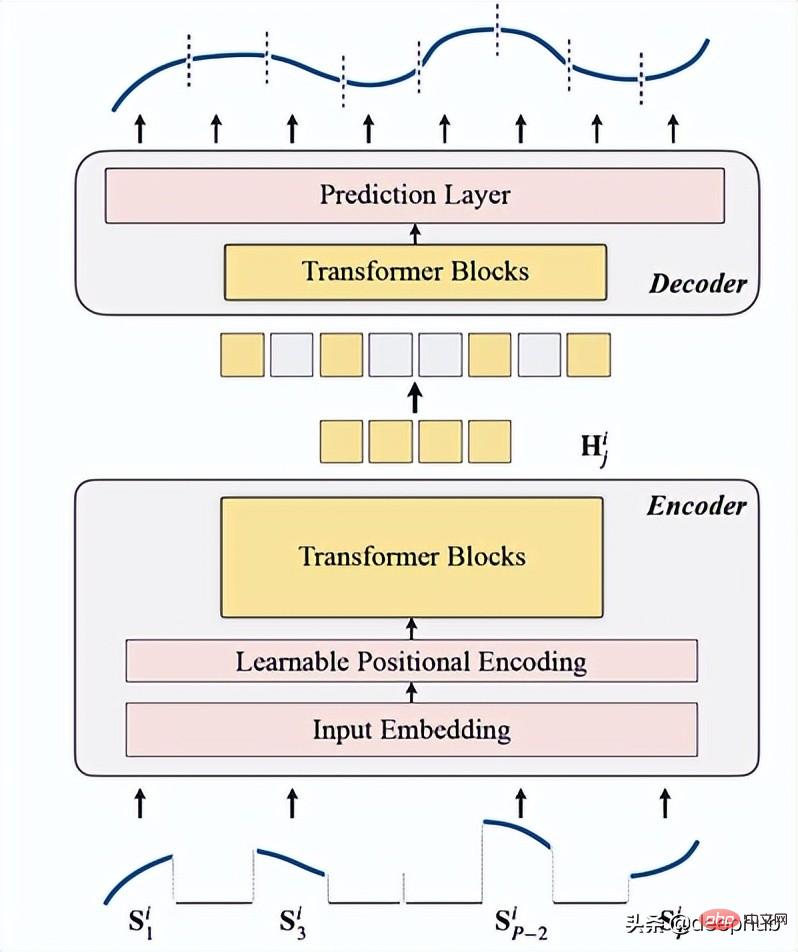
Ce qui suit est l'implémentation du code :
def trunc_normal_(tensor, mean=0., std=1.):<br>__call_trunc_normal_(tensor, mean=mean, std=std, a=-std, b=std)<br>def unshuffle(shuffled_tokens):<br>dic = {}<br>for k, v, in enumerate(shuffled_tokens):<br>dic[v] = k<br>unshuffle_index = []<br>for i in range(len(shuffled_tokens)):<br>unshuffle_index.append(dic[i])<br>return unshuffle_index<br>class TSFormer(nn.Module):<br>def __init__(self, patch_size, in_channel, out_channel, dropout, mask_size, mask_ratio, L=6, distribution='uniform', lm=-1, selected_feature=0, mode='Pretrain', spectral=True):<br>super().__init__()<br>self.patch_size = patch_size<br>self.seleted_feature = selected_feature<br>self.mode = mode<br>self.spectral = spectral<br>self.patch = Patch(patch_size, in_channel, out_channel, spectral=spectral)<br>self.pe = PositionalEncoding(out_channel, dropout=dropout)<br>self.mask = MaskGenerator(mask_size, mask_ratio, distribution=distribution, lm=lm)<br>self.encoder = TransformerLayers(out_channel, L)<br>self.decoder = TransformerLayers(out_channel, 1)<br>self.encoder_2_decoder = nn.Linear(out_channel, out_channel)<br>self.mask_token = nn.Parameter(torch.zeros(1, 1, 1, out_channel))<br>trunc_normal_(self.mask_token, std=.02)<br>if self.spectral:<br>self.output_layer = nn.Linear(out_channel, int(patch_size/2+1)*2)<br>else:<br>self.output_layer = nn.Linear(out_channel, patch_size)<br>def _forward_pretrain(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br><br># mask tokens<br>unmasked_token_index, masked_token_index = self.mask()<br>encoder_input = patches[:, :, unmasked_token_index, :] <br># encoder<br>H = self.encoder(encoder_input) <br># encoder to decoder<br>H = self.encoder_2_decoder(H)<br># decoder<br># H_unmasked = self.pe(H, index=unmasked_token_index)<br>H_unmasked = H<br>H_masked = self.pe(self.mask_token.expand(B, N, len(masked_token_index), H.shape[-1]), index=masked_token_index)<br>H_full = torch.cat([H_unmasked, H_masked], dim=-2) # # B, N, L/P, d<br>H = self.decoder(H_full)<br># output layer<br>if self.spectral:<br># output = H<br>spec_feat_H_ = self.output_layer(H)<br>real = spec_feat_H_[..., :int(self.patch_size/2+1)]<br>imag = spec_feat_H_[..., int(self.patch_size/2+1):]<br>spec_feat_H = torch.complex(real, imag)<br>out_full = torch.fft.irfft(spec_feat_H)<br>else:<br>out_full = self.output_layer(H)<br># prepare loss<br>B, N, _, _ = out_full.shape <br>out_masked_tokens = out_full[:, :, len(unmasked_token_index):, :]<br>out_masked_tokens = out_masked_tokens.view(B, N, -1).transpose(1, 2)<br>label_full = input.permute(0, 3, 1, 2).unfold(1, self.patch_size, self.patch_size)[:, :, :, self.seleted_feature, :].transpose(1, 2) # B, N, L/P, P<br>label_masked_tokens = label_full[:, :, masked_token_index, :].contiguous()<br>label_masked_tokens = label_masked_tokens.view(B, N, -1).transpose(1, 2)<br># prepare plot<br>## note that the output_full and label_full are not aligned. The out_full in shuffled<br>### therefore, unshuffle for plot<br>unshuffled_index = unshuffle(unmasked_token_index + masked_token_index)<br>out_full_unshuffled = out_full[:, :, unshuffled_index, :]<br>plot_args = {}<br>plot_args['out_full_unshuffled'] = out_full_unshuffled<br>plot_args['label_full'] = label_full<br>plot_args['unmasked_token_index'] = unmasked_token_index<br>plot_args['masked_token_index'] = masked_token_index<br>return out_masked_tokens, label_masked_tokens, plot_args<br>def _forward_backend(self, input):<br>B, N, C, L = input.shape<br># get patches and exec input embedding<br>patches = self.patch(input) <br>patches = patches.transpose(-1, -2) <br># positional embedding<br>patches = self.pe(patches)<br>encoder_input = patches # no mask when running the backend.<br># encoder<br>H = self.encoder(encoder_input) <br>return H<br>def forward(self, input_data):<br><br>if self.mode == 'Pretrain':<br>return self._forward_pretrain(input_data)<br>else:<br>return self._forward_backend(input_data)
Après avoir lu cet article, j'ai découvert que cela peut fondamentalement être considéré comme une copie de MAE, ou MAE de séries chronologiques L'étape de prédiction est également similaire à MAE, utilisant la sortie de l'encodeur comme fonctionnalités et fournissant des données de fonctionnalités comme entrée pour les tâches en aval. Si vous êtes intéressé, vous pouvez lire l'article original et jeter un œil au code fourni dans l'article. .
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

