Comment implémenter le parcours graphique en Java

1. Parcours du graphique

Commencez à partir d'un certain sommet du graphique et visitez les sommets restants du graphique, et chaque sommet n'est visité qu'une seule fois

Il existe deux types de parcours de graphique : le parcours en profondeur DFS et le parcours en largeur en premier. traversée BFS

2. Traversée en profondeur d'abord

Traversée en profondeur d'abord avec la profondeur en premier, cela signifie aller jusqu'au bout à chaque fois. Semblable au parcours de pré-ordre d'un arbre binaire

Idées :

1. Effectuez un parcours en profondeur à partir d'un certain sommet et marquez le sommet comme visité

2 Sélectionnez n'importe quel chemin à partir du sommet et traversez. jusqu'à la fin, et marquez les sommets visités

3. Après avoir parcouru jusqu'à la fin à l'étape 2, revenez au sommet précédent et répétez l'étape 2

4 Fin du parcours de tous les sommets

Selon l'idée de traversée, nous. Je peux savoir qu'il s'agit d'un processus récursif. En fait, DFS est fondamentalement la même chose que le retour en arrière.

Traversée :

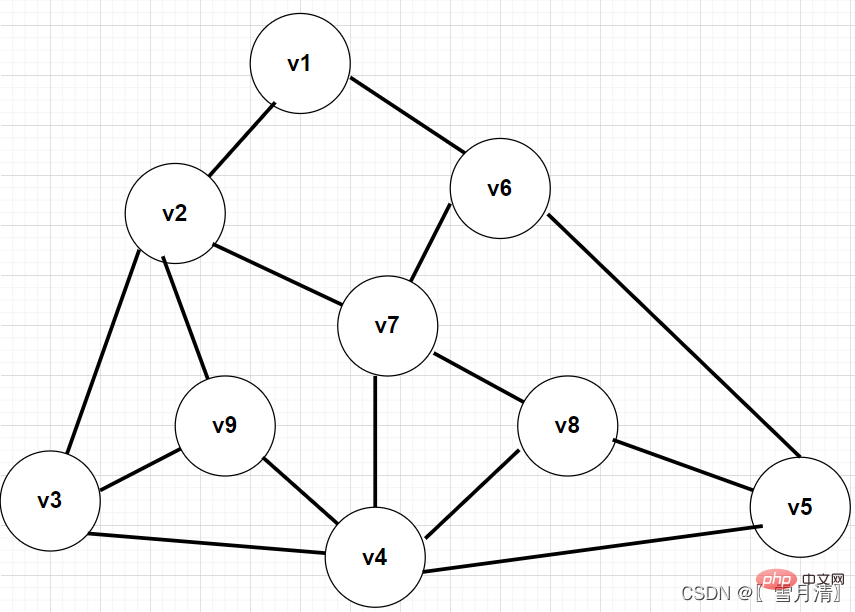
Prenez cette photo comme exemple pour effectuer une traversée en profondeur d'abord

	static void dfs(int[][] graph,int idx,boolean[]visit) {
		int len = graph.length;
		//访问过
	 if(visit[idx]) return;
	 //访问该顶点
	 System.out.println("V"+idx);
	 //标志顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
	 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
	 //递归进行dfs遍历
		 dfs(graph, i, visit);
		 }
	 }
			
	}

Résultats de traversée :

V1

V2

V3

V4

V5

V6

V7

V8

V9

Le code pour créer le graphe :

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit);
		
	}

3. Utilisez DFS pour déterminer s'il y a un cycle dans le graphe orienté

Idée : lors du passage d'un certain sommet, s'il est en plus du sommet précédent. , il y a d'autres sommets connectés qui ont été visités, alors il doit y avoir un cycle

	//默认无环
   static boolean flag = false;
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			
		}
	 //标记数组 true为访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit,1);
		if(flag) 
			System.out.println("有环");
		
	}
	
	static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
		int len = graph.length;
	
	 System.out.println("V"+idx);
	 //标记顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
		 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
		 if( !visit[i] ) {
		 dfs(graph, i, visit,idx);
		 }
		 else if(idx != i) {
			 flag = true;
		 }
		 }
	 }
	
	 
	}

Remarque : c'est un graphe orienté pour déterminer si un cycle existe, et un graphe non orienté n'a aucun sens pour déterminer si un cycle existe, car le les sommets de deux chemins existants peuvent être des cycles

4. Traversée en largeur en premier

La traversée en largeur consiste à parcourir la largeur (largeur) en premier. Semblable au parcours par ordre de niveau d'un arbre binaire

Idées :

1. Effectuez un parcours en largeur en premier à partir d'un certain sommet et marquez le sommet comme visité

2 Visitez tous les sommets connectés au sommet qui l'ont été. n'a pas été visité, et marquez les sommets visités

3. Répétez les étapes 1 et 2 en commençant par les sommets visités à l'étape 2

4. Fin du parcours de tous les sommets

Utilisez la file d'attente pour faciliter la traversée et l'ordre de la file d'attente. est le résultat du parcours en largeur en premier

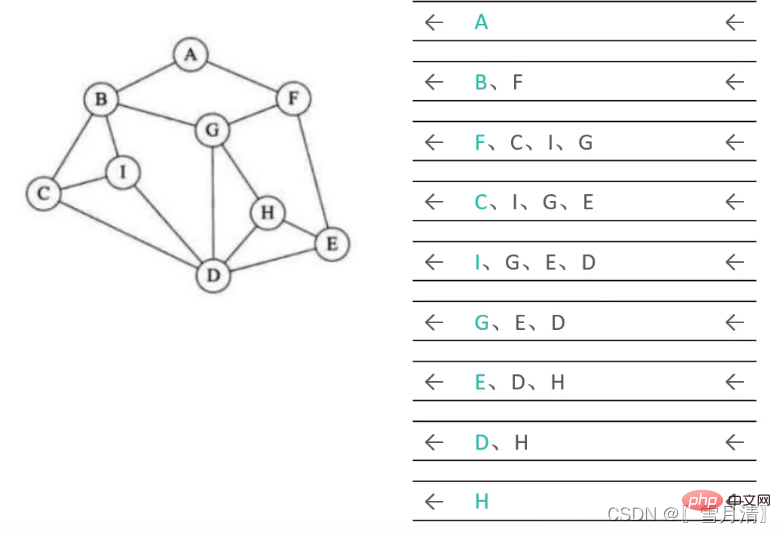
Traversal

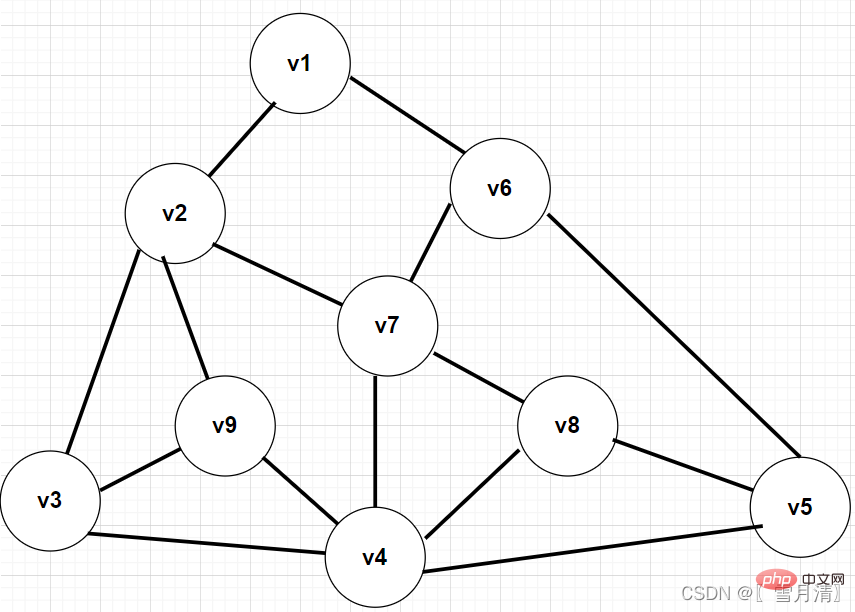
Prenez cette image comme exemple, utilisez la matrice de contiguïté pour créer le graphique et effectuez le parcours BFS

	static void bfs(int[][] graph) {		
		int len = graph.length;
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[len];
		//辅助队列
		Queue<Integer> queue = new LinkedList<>();
		
		queue.offer(1);
		visit[1] = true;
		
		while(!queue.isEmpty()) {
			int num = queue.poll();
			System.out.println("V"+num);
					
			//遍历该顶点所有相连顶点
			for(int i = 1;i < len;i++) {
				//相连并且没有被访问过
				if(graph[num][i] == 1 && !visit[i]) {
					queue.offer(i);
					visit[i] = true;				
				}
			}
		}	
	}

Résultat du parcours :

V1

V2

V6

V3

V7

V9

V5

V4

V8

Code pour créer un graphique

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		bfs(graph);
	}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!