Comment implémenter un arbre binaire en Python

Python implémente un arbre binaire

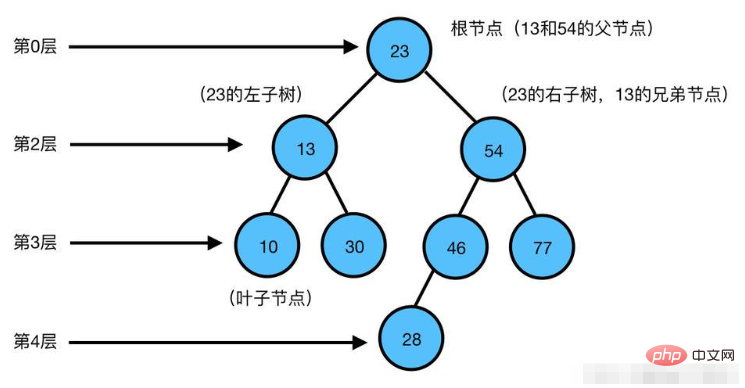
Python peut implémenter un arbre binaire en utilisant une programmation orientée objet en définissant une classe de nœuds d'arbre binaire. Chaque nœud contient un élément de données, des pointeurs de nœuds enfants gauche et droit et certaines méthodes de fonctionnement, telles que l'insertion de nœuds, la recherche de nœuds, la suppression de nœuds, etc.

Ce qui suit est un exemple simple d'implémentation d'arbre binaire :

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return str(data) + " Not Found"
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return str(data) + " Not Found"
            return self.right.find(data)
        else:
            return str(self.data) + " is found"

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

Dans le code ci-dessus, la classe Node définit un nœud, y compris les données de l'élément de données, et les pointeurs de nœud enfant gauche et droit gauche et droit. La méthode insert est utilisée pour insérer des nœuds dans un arbre binaire, la méthode find est utilisée pour déterminer si un nœud spécifique existe dans l'arbre binaire et la méthode inorder_traversal est utilisée pour effectuer un parcours dans l'ordre de l'arbre binaire.

Voici comment utiliser cette classe Node pour créer un arbre binaire :

root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 查找节点

print(root.find(70)) # Output: 70 is found
print(root.find(90)) # Output: 90 Not Found

# 中序遍历
print(root.inorder_traversal(root)) # Output: [20, 30, 40, 50, 60, 70, 80]

Dans le code ci-dessus, un nœud racine racine est d'abord créé, puis la méthode insert est utilisée pour insérer le nœud dans l'arbre, et enfin la méthode find est utilisé pour trouver le nœud et la méthode inorder_traversal est utilisée Effectuer un parcours dans l'ordre d'un arbre binaire.

En plus des méthodes d'insertion, de recherche et de parcours, les arbres binaires ont également d'autres méthodes de fonctionnement, telles que la suppression de nœuds, la détermination s'il s'agit d'un arbre de recherche binaire, le calcul de la profondeur de l'arbre, etc. Ce qui suit est un exemple de code d'arbre binaire légèrement plus complet :

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
            return self.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is None:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

Dans cet exemple, nous avons ajouté la méthode delete pour supprimer le nœud spécifié ; la méthode minimale pour trouver le plus petit nœud dans l'arborescence pour déterminer si la méthode is_bst ; L'arbre actuel est une méthode binaire de recherche de hauteur d'arbre pour calculer la profondeur de l'arbre.

Nous pouvons utiliser le code suivant pour tester la nouvelle méthode :

# 创建二叉树
root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 删除节点
print("Deleting node 20:")
root.delete(20)
print(root.inorder_traversal(root))

# 判断是否为二叉搜索树
print("Is it a BST?:", root.is_bst())

# 计算树的深度
print("Tree height:", root.height(root))

De cette façon, nous avons réalisé une implémentation d'arbre binaire relativement complète et avons également démontré comment utiliser des idées de programmation orientée objet en Python pour implémenter une structure de données.

Enfin, le code complet d'implémentation de la classe d'arbre binaire est joint :

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
            return self.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is None:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

if __name__ == '__main__':
    # 创建二叉树
    root = Node(50)
    root.insert(30)
    root.insert(20)
    root.insert(40)
    root.insert(70)
    root.insert(60)
    root.insert(80)

    # 删除节点
    print("Deleting node 20:")
    root.delete(20)
    print(root.inorder_traversal(root))

    # 判断是否为二叉搜索树
    print("Is it a BST?:", root.is_bst())

    # 计算树的深度
    print("Tree height:", root.height(root))

Après avoir exécuté le code, vous pouvez obtenir le résultat suivant :

Suppression du nœud 20 :
[30, 40, 50, 60, 70, 80]
Est-ce un BST ? : Vrai
Hauteur de l'arbre : 3

Cet exemple inclut l'insertion, la recherche, la suppression, le parcours, la détermination s'il s'agit d'un arbre de recherche binaire et le calcul de la profondeur de l'arbre, etc.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!