Chaque bit binaire est décalé vers la gauche d'un certain nombre de bits, le bit élevé est ignoré et le bit élevé est complété avec le signe bit ou zéro, selon la situation Compilateur |
|
** Tout d'abord, il doit être clair que les opérations sur les bits ne peuvent opérer que sur des entiers**
En jdk, le décalage à droite Java est une opération de décalage à droite arithmétique
** La priorité des opérations sur les bits est très faible. Il est donc préférable d'utiliser des parenthèses**
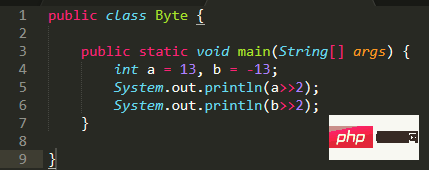
La sortie du code ci-dessus :
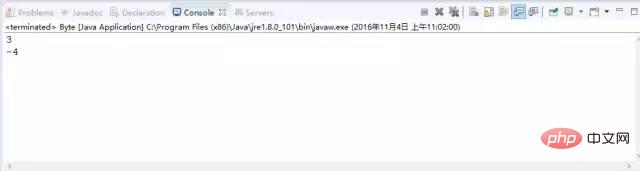
Analysons pourquoi ce résultat est affiché :
Tout d'abord, pour 13. , on écrit son Binaire : 0000 1101
Décalage à droite de deux places : 0000 0011. Puisque le décalage à droite en jdk est un décalage arithmétique à droite, les bits hauts sont remplis de 00, et le résultat est 3
Pour -13, le code binaire : 1111 0011
Décaler vers la droite de deux bits, compléter le bit de signe dans l'ordre supérieur, 1111 1100, le résultat est -4
Commun conseils pour les opérations sur les bits
Les opérations sur bits sont souvent utilisées pour certaines petites opérations, car elles ne peuvent opérer que sur des nombres entiers, leurs utilisations sont donc limitées, mais certaines astuces couramment utilisées valent la peine d'être maîtrisées, comme juger les pairs et les impairs, échanger deux nombres, échanger des signes, trouver valeurs absolues, etc. Nous les présenterons un par un ci-dessous.
Juge parité
La différence entre la parité et l'égalité se reflète en binaire, c'est-à-dire que la fin est 0, 1. Évidemment, lorsque la fin est 0, c'est un nombre pair, et lorsque la fin est 1, il est le dernier nombre impair. Ainsi, la méthode pour déterminer la parité est la suivante :
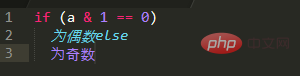
Un petit programme de test :
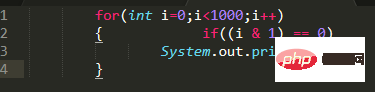
Le programme ci-dessus produira tous les nombres pairs dans les 1000
Échangez deux nombres
Utilisez des opérations sur bits pour échanger deux nombres. L'avantage est qu'il n'y a pas besoin de la troisième variable temporaire (la limitation est que seules les variables entières peuvent être échangées)

Analysez comment l'échange se produit :
D'abord a^=b, c'est-à-dire a=(a^ b);
b^= a signifie b=b(ab). Puisque l'opération satisfait la loi commutative, b(ab)=bb^a. Un nombre qui est XORé avec lui-même doit être 0, car il doit être égal à lui-même. Donc, si un nombre est XORé avec 0, 1 et 0 seront toujours 1, et 0 et 0 seront toujours 0, donc évidemment un nombre et. 0 Après XOR, bien sûr, c'est toujours lui-même. Donc à ce moment, b se voit attribuer la valeur a.
La dernière étape, a^=b est a=ab Puisque les deux étapes précédentes montrent que a=(ab), b=a, a=ab signifie a=(ab)^a. . Par conséquent, a se verra attribuer la valeur de b.
Conversion du signe
La conversion du signe est évidemment très simple. D'après le code complémentaire similaire, il suffit de prendre l'inverse et d'en ajouter un.

Trouver la valeur absolue
La recherche de la valeur absolue est mise en œuvre sur la base du changement de signe. Il suffit de déterminer d'abord s'il s'agit d'un nombre négatif, changez le signe. Sinon, revenez directement.
Pour déterminer s'il est positif ou négatif, vous pouvez déterminer directement son bit de signe, le décaler de 31 bits vers la droite, obtenir le bit de signe et déterminer s'il est positif ou négatif
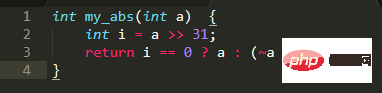
Pour n'importe quel nombre, XOR avec 0 restera inchangé et XOR avec -1, qui est 0xFFFFFFFF, sera équivalent à la négation. Par conséquent, la valeur absolue peut également être obtenue en effectuant un XOR sur a avec i puis en soustrayant i (car i est 0 ou -1, donc soustraire i signifie soit ajouter 0, soit ajouter 1). Par conséquent, le code ci-dessus peut être optimisé :
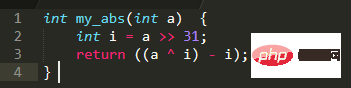
Application des opérations sur les bits
Les opérations sur les bits pour implémenter les opérations A+B sont des questions d'algorithme courantes.
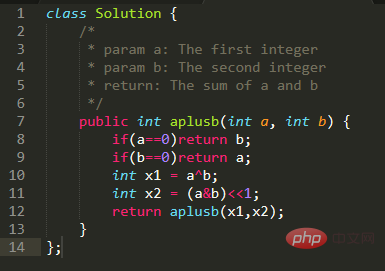
Le code ci-dessus réalise l'addition de deux nombres à l'aide d'opérations sur bits sans utiliser l'opérateur +.
Expliquons maintenant le principe de l'addition de deux nombres par opérations sur bits
Tout d'abord, en décimal, on sait que, 7+8, la somme sans retenue est 5, et la retenue est 1, alors on peut ajouter 5+1 selon à la somme sans report et report *10 calcule le résultat final 15.
Semblable au binaire, cette méthode peut également être adoptée
Par exemple
a = 3, b = 6
a : 0011
b : 0110
Sans report et : 0101 Soit 5
Carry : 0010 Soit 2
Donc a+ b devient 5 + (2 1 0001
4sans report et 1001 = 9
carry 0000 = 0
Quand le report est 0, la somme sans report est 9, qui est la somme de a + b.
Vous pouvez constater que ce qui précède est un processus récursif, il n'est donc pas difficile d'écrire le code. Trouver la somme sans retenue de deux nombres n’est en réalité qu’une opération XOR des deux nombres.










