Maison >Java >javaDidacticiel >Exemple d'analyse de l'arbre de Huffman en Java
Exemple d'analyse de l'arbre de Huffman en Java
- 王林avant
- 2023-04-28 23:16:231021parcourir
Arbre de Huffman
1. Introduction de base

2. Plusieurs concepts et exemples importants de l'arbre de Huffman
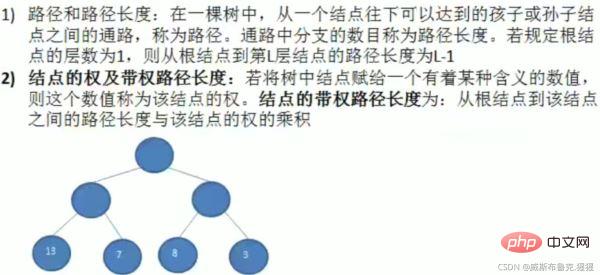
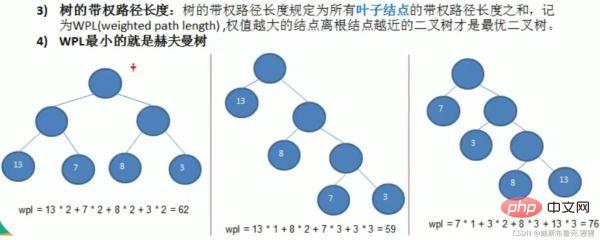
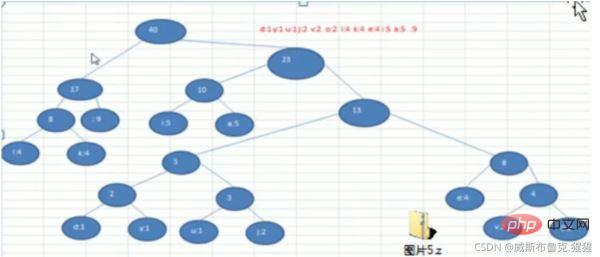
Étapes pour construire un arbre de Huffman

Exemples : Prendre arr = {1 3 6 7 8 13 29}
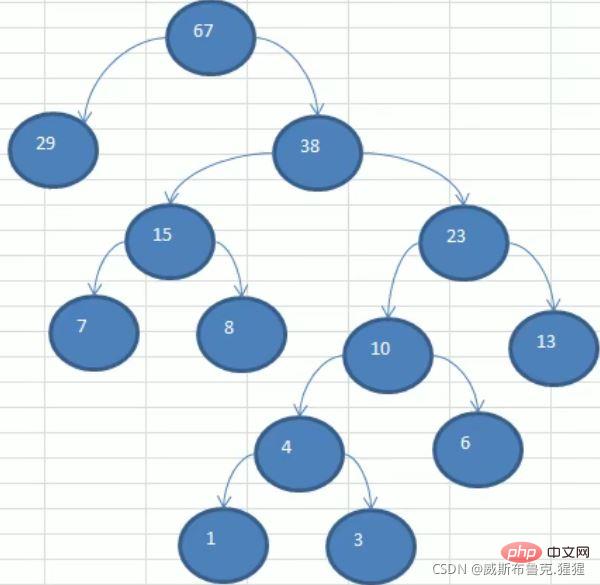
public class HuffmanTree {
public static void main(String[] args) {
int[] arr = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root);
}
// 编写一个前序遍历的方法
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("树是空树,无法遍历~~");
}
}
// 创建赫夫曼树的方法
/**
* @param arr 需要创建成霍夫曼树的数组
* @return 创建好后的霍夫曼树的root节点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1.遍历 arr 数组
// 2.将 arr 的每个元素构成一个Node
// 3.将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
// 排序从小到大
Collections.sort(nodes);
System.out.println("nodes = " + nodes);
// 取出根节点权值最小的两颗二叉树
//注意:如果是从大到小排列的:就应该取倒数第一个和倒数第二个
// (1) 取出权值最小的节点(二叉树)
Node leftNode = nodes.get(0);
// (2) 取出权值第二小的节点(二叉树)
Node rightNode = nodes.get(1);
// (3) 构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
// (4) 从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
// (5) 将parent加入到nodes
nodes.add(parent);
}
// 返回赫夫曼树的root节点
return nodes.get(0);
}
}
//创建节点类
//为了让Node对象支持排序Collections集合排序
//让Node实现Comparable接口
class Node implements Comparable<Node> {
int value;// 节点权值
Node left;// 指向左子节点
Node right;// 指向右子节点
public Node(int value) {
this.value = value;
}
// 写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// 表示从小到大排列
return this.value - o.value;
}
}Codage Huffman
1. Introduction de base

2. Analyse des principes


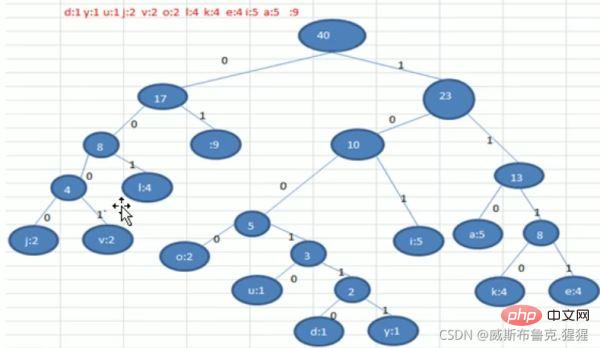


6) Remarque :
La longueur originale est de 359, compressée (359 - 133) / 359 = 62,9%
Cet encodage satisfait à l'encodage de préfixe, c'est-à-dire que l'encodage de caractères ne peut pas être le préfixe d'autres encodages de caractères. Cela ne provoquera pas d'ambiguïté de correspondance ;
L'encodage Huffman est une solution de traitement de compression sans perte
Remarque :


Précautions concernant l'encodage Huffman pour les fichiers compressés
1 ) Si le fichier lui-même est compressé , alors l'utilisation du codage Huffman ne modifiera pas de manière significative l'efficacité de la compression, comme les vidéos, ppt et autres fichiers
2) Le codage Huffman est traité par octets, il peut donc traiter tous les fichiers (fichiers binaires, fichiers texte)
3) Si il n'y a pas beaucoup de données répétées dans le contenu d'un fichier, l'effet de compression ne sera pas évident.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

