Comment implémenter un arbre de hauteur minimale en Java

Le problème nécessite

Un arbre est un graphe non orienté, dans lequel deux sommets quelconques sont reliés par un seul chemin. En d’autres termes, tout graphe connecté sans cycles simples est un arbre.

Vous recevez un arbre contenant n nœuds, étiquetés de 0 à n - 1. Étant donné un nombre n et une liste d'arêtes avec n - 1 arêtes non orientées (chaque arête est une paire d'étiquettes), où arêtes[i] = [ai, bi] signifie qu'il y a une arête entre les nœuds ai et bi dans l'arbre. bord.

Vous pouvez sélectionner n'importe quel nœud de l'arborescence comme racine. Lorsque le nœud x est sélectionné comme nœud racine, laissez la hauteur de l’arbre résultat être h. Parmi tous les arbres possibles, l'arbre avec la hauteur minimale (c'est-à-dire min(h)) est appelé l'arbre de hauteur minimale.

Veuillez trouver tous les arbres de hauteur minimale et renvoyer leur liste d'étiquettes de nœuds racines dans n'importe quel ordre.

La hauteur d'un arbre fait référence au nombre d'arêtes sur le chemin descendant le plus long entre le nœud racine et les nœuds feuilles.

Exemple 1 :

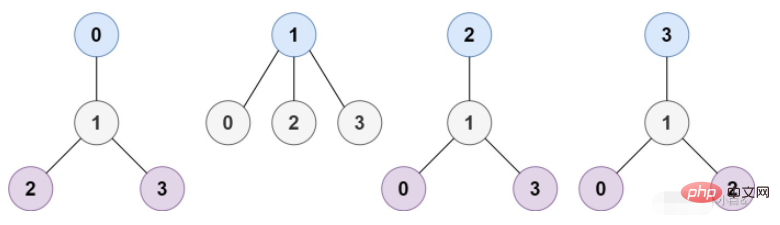
Entrée : n = 4, bords = [[1,0],[1,2],[1,3]]
Sortie : [1]
Explication : Comme indiqué dans le figure , lorsque la racine est le nœud d'étiquette 1, la hauteur de l'arbre est 1, qui est le seul arbre de hauteur minimale.

Exemple 2 :

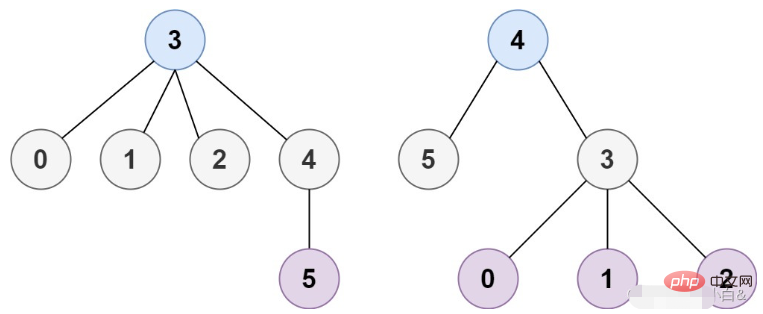
Entrée : n = 6, bords = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Sortie : [3,4]

Invite :
1 edges.length == n - 1
0 Tous (ai, bi) sont différents les uns des autres
L'entrée donnée est garantie d'être un arbre, et il n'y aura pas d'arêtes en double

Idées de résolution de problèmes

  À partir des deux figures ci-dessus, nous pouvons tirer une conclusion : ce qui doit être résolu dans la question, c'est le nœud central de l'arbre, et chaque arbre n'aura pas plus de deux nœuds centraux.

  Et si nous voulons obtenir le nœud central dans l'arbre, nous pouvons FBS couche par couche (c'est-à-dire couper les nœuds feuilles avec un degré de sortie d'une couche par couche) jusqu'à ce que la dernière couche soit couper, alors nous pouvons Le résultat est sorti !

Algorithme

class Solution {
    public List<Integer> findMinHeightTrees(int n, int[][] edges) {
        List<Integer> res = new ArrayList<Integer>();
        //如果只有一个节点，则它就是最小高度树
        if(n == 1){
            res.add(0);
            return res;
        }

        //每个节点的邻居数量
        int [] degree = new int[n];
        //每个节点的邻居
        HashMap<Integer,List<Integer>> map = new HashMap<>();

        for(int [] edge : edges){
            int a = edge[0];
            int b = edge[1];

            degree[a]++;
            degree[b]++;

            if(map.get(a) == null){
                map.put(a,new ArrayList<Integer>());//key:节点   value:邻居
            }

            if(map.get(b) == null){
                map.put(b,new ArrayList<Integer>());//key:节点   value:邻居
            }

            map.get(a).add(b);
            map.get(b).add(a);
        }

        //建立队列
        LinkedList<Integer> leafNodes = new LinkedList<Integer>();//表示叶子节点
        //将所有度为1的节点入队
        for(int i = 0;i < degree.length;i++){
            if(degree[i] == 1){
                leafNodes.add(i);
            }
        }

        while(leafNodes.size() > 0){
            res.clear();
            //每一层节点的数量
            int size = leafNodes.size();

            for(int i = 0;i < size;i++){
                int leaf = leafNodes.poll();
                //将当前节点加入到结果集
                res.add(leaf);

                List<Integer> neighbors = map.get(leaf);
                //将出度减一，也就是将最外层的叶子节点剪掉
                for(int neighbor : neighbors){
                    degree[neighbor]--;
                    if(degree[neighbor] == 1){
                        //叶子节点入队
                        leafNodes.add(neighbor);
                    }
                }
            }
        }
        return res;
    }
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!