Explication détaillée d'exemples d'ajout, d'insertion, de suppression et de création d'arbres de recherche binaires Java

①Concept

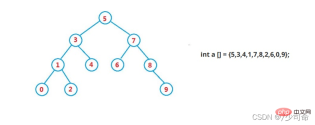
L'arbre de recherche binaire est également appelé arbre de tri binaire. Il s'agit soit d'un arbre vide**, soit d'un arbre binaire avec les propriétés suivantes :

Si son sous-arbre gauche n'est pas vide, alors les valeurs ​​de tous les nœuds du sous-arbre de gauche sont inférieures à la valeur du nœud racine

Si son sous-arbre droit n'est pas vide, alors les valeurs de tous les nœuds du sous-arbre droit sont supérieures à la valeur du nœud racine

Ses sous-arbres gauche et droit sont également respectivement. opération - insérer

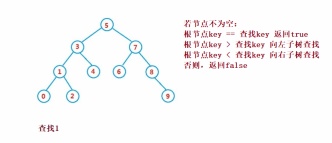
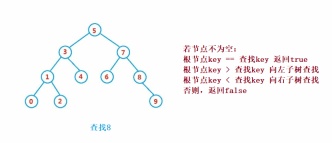
public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

④Opération-Supprimer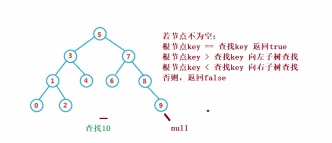

L'opération de suppression est plus compliquée, mais il est relativement facile de comprendre son principe

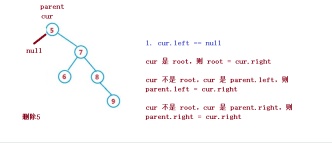
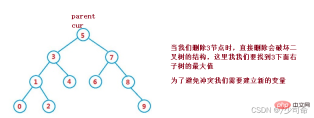
Supposons que le nœud à supprimer soit cur, et le nœud parent du nœud à supprimer est parent

1. cur.left == null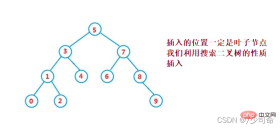

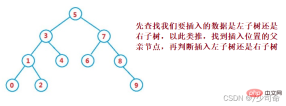1 cur est root, alors root = cur.right

2. , alors parent.left = cur.right

3. cur n'est pas root, cur est parent.right, puis parent.right = cur.right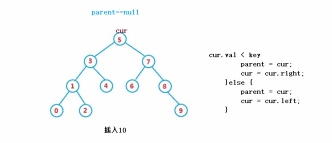

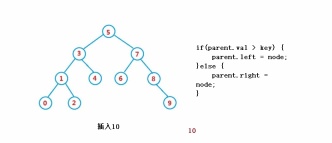
2. right == null

1. cur est root, puis root = cur .left

2 cur n'est pas root, cur est parent.left, puis parent.left = cur.left

3. cur est parent.right, alors parent.right = cur.left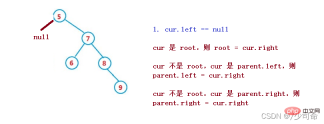

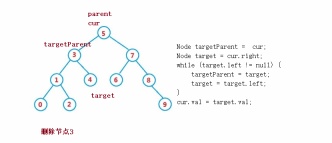
Deuxième Cette situation est la même que la première, sauf dans le sens opposé Plus de dessin ici

3. right != null

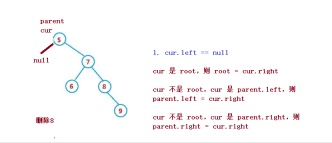
Vous devez utiliser la méthode de substitution pour supprimer, c'est-à-dire dans son sous-arbre droit. Trouvez le premier nœud dans l'ordre du milieu (avec le plus petit code clé), remplissez-le avec sa valeur dans le nœud supprimé, et puis traitez le problème de suppression du nœud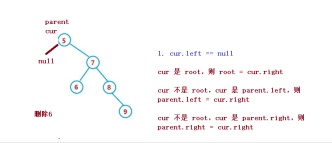

Lorsque nous sommes dans la situation où ni le sous-arbre gauche ni le sous-arbre droit ne sont vides, la suppression est effectuée ci-dessous. La suppression du nœud détruira la structure de l'arbre, la méthode du bouc émissaire est donc utilisée pour résoudre. Le processus de suppression réel est toujours les deux situations ci-dessus. Les propriétés de l'arbre binaire de recherche sont toujours utilisées ici

  public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }

⑤Analyse des performances

Les opérations d'insertion et de suppression doivent être recherchées en premier. L'efficacité de la recherche représente la performance de chaque opération dans l'arbre de recherche binaire.

Pour un arbre de recherche binaire avec n nœuds, si la probabilité de rechercher chaque élément est égale, alors la longueur de recherche moyenne de l'arbre de recherche binaire est fonction de la profondeur du nœud dans l'arbre de recherche binaire, c'est-à-dire plus le nœud est profond, plus il y a de comparaisons.

Mais pour un même jeu de codes clés, si l'ordre d'insertion de chaque code clé est différent, des arbres de recherche binaires avec des structures différentes peuvent être obtenus :

Dans le cas optimal, l'arbre de recherche binaire est un arbre binaire complet, et son no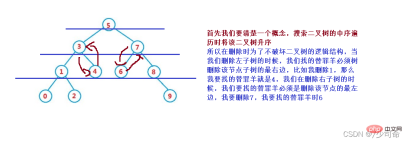mbre moyen de comparaisons est :

Dans le pire des cas, l'arbre de recherche binaire dégénère en un arbre à une seule branche, et son nombre moyen de comparaisons est :

⑥完整代码

public class TextDemo {
 
    public static class Node {
        public int val;
        public Node left;
        public Node right;
 
        public Node (int val) {
            this.val = val;
        }
    }
 
 
    public Node root;
 
    /**
     * 查找
     * @param key
     */
    public Node search(int key) {
        Node cur = root;
        while (cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(cur.val < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }
 
    /**
     *
     * @param key
     * @return
     */
    public boolean insert(int key) {
        Node node = new Node(key);
        if(root == null) {
            root = node;
            return true;
        }
 
        Node cur = root;
        Node parent = null;
 
        while(cur != null) {
            if(cur.val == key) {
                return false;
            }else if(cur.val < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //parent
        if(parent.val > key) {
            parent.left = node;
        }else {
            parent.right = node;
        }
 
        return true;
    }
 
    public void remove(Node parent,Node cur) {
        if(cur.left == null) {
            if(cur == root) {
                root = cur.right;
            }else if(cur == parent.left) {
                parent.left = cur.right;
            }else {
                parent.right = cur.right;
            }
        }else if(cur.right == null) {
            if(cur == root) {
                root = cur.left;
            }else if(cur == parent.left) {
                parent.left = cur.left;
            }else {
                parent.right = cur.left;
            }
        }else {
            Node targetParent =  cur;
            Node target = cur.right;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }
 
    public void removeKey(int key) {
        if(root == null) {
            return;
        }
        Node cur = root;
        Node parent = null;
        while (cur != null) {
            if(cur.val == key) {
                remove(parent,cur);
                return;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
 
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!