Maison >Java >javaDidacticiel >Quelles sont les méthodes de parcours récursives et non récursives de l'arbre binaire Java ?
Quelles sont les méthodes de parcours récursives et non récursives de l'arbre binaire Java ?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-24 13:04:141458parcourir
Avant-propos
Les méthodes de parcours des arbres binaires sont divisées en parcours de pré-ordre, parcours dans l'ordre, parcours ultérieur et parcours par ordre de niveau.
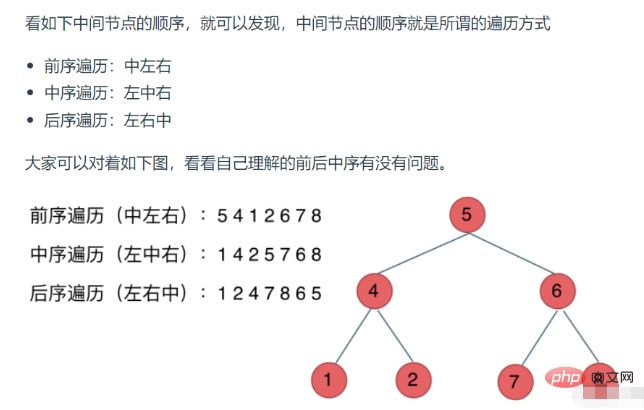
1. Parcours récursif
Pour la récursivité, nous devons parler des trois éléments de la récursion : Prenons l'exemple du parcours de précommande
Paramètres d'entrée récursifs et valeurs de retour
Parce que nous devons imprimer les valeurs des nœuds de parcours de précommande, donc les paramètres Vous devez transmettre la valeur du nœud dans la liste. En dehors de cela, il n'est pas nécessaire de traiter des données et il n'est pas nécessaire d'avoir une valeur de retour, donc le retour. Le type de la fonction récursive est nul. Le code est le suivant :
public void preorder(TreeNode root, List<Integer> result)
Déterminer la condition de terminaison
En récursion Dans le processus, comment se termine la récursion Bien sûr, le nœud actuellement parcouru est vide, alors le niveau actuel de ? la récursion est sur le point de se terminer, donc si le nœud actuellement parcouru est vide, revenez simplement directement
if (root == null) return;
Logique de boucle monocouche
Le parcours de pré-ordre est l'ordre du milieu et de gauche, donc la logique de la récursivité à un seul niveau doit prendre la valeur du nœud du milieu en premier. Le code est le suivant :
result.add(root.val); preorder(root.left, result); preorder(root.right, result);
// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {
public List preorderTraversal(TreeNode root) {
List result = new ArrayList();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);//先保存中间节点
preorder(root.left, result); //处理左边节点
preorder(root.right, result); //处理右边节点
}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {
public List inorderTraversal(TreeNode root) {
List res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List list) {
if (root == null) {
return;
}
inorder(root.left, list); //先处理左边节点
list.add(root.val); //保存中间当前的节点
inorder(root.right, list);//先处理右边节点
}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {
public List postorderTraversal(TreeNode root) {
List res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List list) {
if (root == null) {
return;
}
postorder(root.left, list); //先处理左边节点
postorder(root.right, list); //再处理右边节点
list.add(root.val); //保存最后
}
} 2 Traversée non itérative
//前序遍历
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack();
if (root == null) return res;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.right != null) { //先将右孩子入栈,因为它在最后
stack.push(node.right);
}
if (node.left != null) { //左孩子入栈再出栈
stack.push(node.left);
}
}
return res;
}
}
//中序遍历
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
//如果可以,一直往左下探
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop(); //弹出来的肯定是叶子节点或中间节点
res.add(cur.val); //将这个节点加入list
cur = cur.right; //查看当前节点是否有右节点,如果右,肯定是中间节点,如果没有,就是叶子节点,继续弹出就可以
}
}
return res;
}
}
//后序遍历
//再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.left != null) stack.push(node.left); // 相对于前序遍历,这更改一下入栈顺序 (空节点不入栈)
if (node.right != null) stack.push(node.right);// 空节点不入栈
}
Collections.reverse(res); // 将结果反转之后就是左右中的顺序了
return res;
}
}3.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

