Comparez les méthodes de prévision de séries chronologiques basées sur SARIMA, XGBoost et CNN-LSTM.

Utilisation des tests statistiques et de l'apprentissage automatique pour analyser et prédire les tests et comparaisons des performances de la production d'énergie solaire

Cet article abordera les techniques permettant d'obtenir une valeur tangible à partir d'ensembles de données en utilisant des tests d'hypothèses, l'ingénierie des fonctionnalités, des méthodes de modélisation de séries chronologiques, etc. J'aborderai également des questions telles que la fuite de données et la préparation des données pour différents modèles de séries chronologiques, et effectuerai des tests comparatifs de trois prévisions de séries chronologiques courantes.

Introduction

La prévision de séries chronologiques est un sujet fréquemment étudié. Ici, nous utilisons les données de deux centrales solaires pour étudier ses lois et réaliser une modélisation. Abordez ces problèmes en les réduisant d'abord en deux questions :

1. Est-il possible d'identifier les modules solaires sous-performants ?
2. Est-il possible de prédire la production d'énergie solaire sur deux jours ?

Avant de continuer à répondre à ces questions, comprenons d'abord comment les centrales solaires produisent de l'électricité.

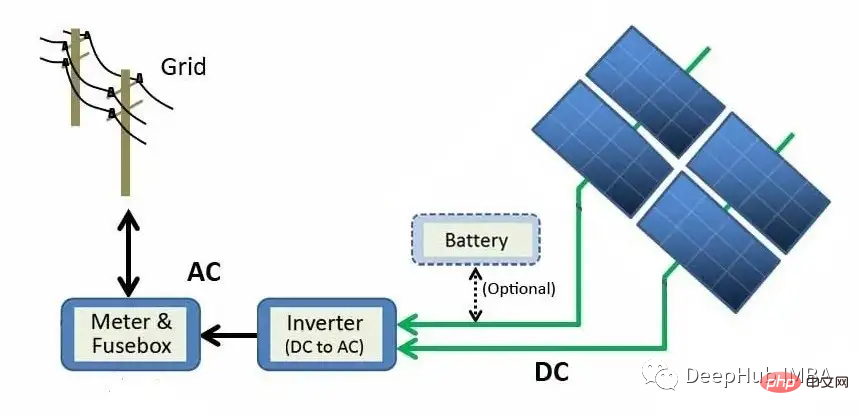
Le schéma ci-dessus décrit le processus de génération des modules de panneaux solaires au réseau. L'énergie solaire est directement convertie en énergie électrique grâce à l'effet photoélectrique. Lorsque des matériaux tels que le silicium (le matériau semi-conducteur le plus courant dans les panneaux solaires) sont exposés à la lumière, les photons (particules subatomiques d'énergie électromagnétique) sont absorbés et des électrons libres sont libérés, créant ainsi un courant continu (CC). À l’aide d’un onduleur, l’énergie CC est convertie en courant alternatif (AC) et envoyée au réseau, où elle peut être distribuée aux foyers.

Données

Les données brutes sont constituées de deux fichiers CSV (valeurs séparées par des virgules) pour chaque centrale solaire. Un document montre le processus de production d'électricité et l'autre montre les mesures enregistrées par les capteurs du parc solaire. Les deux ensembles de données pour chaque centrale solaire ont été organisés dans un pandas df.

Les données de la centrale solaire 1 (SP1) et de la centrale solaire 2 (SP2) ont été collectées toutes les 15 minutes du 15 mai 2020 au 18 juin 2020. Les ensembles de données SP1 et SP2 contiennent les mêmes variables.

• Date Heure - un intervalle de 15 minutes
• Température ambiante - la température de l'air autour du module
• Température du module - la température du module
• Irradiation - le rayonnement sur le module
• Puissance CC (kW) - DC
• Puissance AC ( kW) - AC
• Rendement quotidien - Production d'énergie quotidienne totale
• Rendement total - Sortie cumulée de l'onduleur
• ID de la plante - Identification unique de la centrale solaire
• ID du module - Identification unique de chaque module

Des capteurs météorologiques sont utilisés pour enregistrer la température ambiante, la température du module et le rayonnement de chaque centrale solaire.

Pour cet ensemble de données, la puissance CC sera la variable dépendante (variable cible). Notre objectif est d'essayer de trouver des modules solaires sous-performants.

Deux df indépendants pour l'analyse et la prédiction. La seule différence est que les données utilisées pour les prévisions sont rééchantillonnées à intervalles horaires, tandis que la trame de données utilisée pour l'analyse contient des intervalles de 15 minutes.

Nous supprimons d’abord l’ID de l’usine car il n’ajoute aucune valeur à la réponse à la question ci-dessus. Les ID de module sont également supprimés de l’ensemble de données de prédiction. Les tableaux 1 et 2 montrent des exemples de données.

Avant de continuer à analyser les données, nous avons fait quelques hypothèses sur la centrale solaire, notamment :

• L'instrument d'acquisition de données est sans défaut
• Le module est nettoyé régulièrement (en ignorant l'impact de maintenance)
• Deux solaires Il n'y a aucun problème d'occlusion autour de la centrale électrique

Analyse exploratoire des données (EDA)

Pour ceux qui débutent dans la science des données, l'EDA est une étape cruciale dans la compréhension des données en traçant des visualisations et en effectuant des tests statistiques. Nous pouvons d’abord observer les performances de chaque centrale solaire en traçant le courant continu et alternatif pour SP1 et SP2.

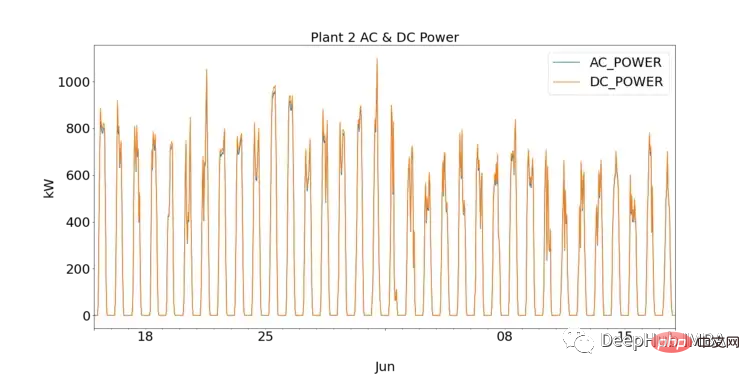
SP1 montre une puissance CC d'un ordre de grandeur supérieure à celle de sp2. En supposant que les données collectées par SP1 sont correctes et que l'instrument utilisé pour enregistrer les données n'est pas défectueux, cela indique que l'onduleur du SP1 doit être étudié plus en profondeur

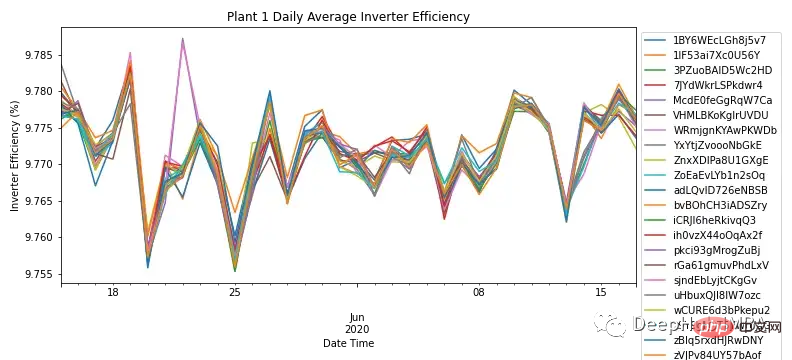
en agrégeant les puissances AC et DC selon la fréquence quotidienne de Pour chaque module, la figure 3 montre l'efficacité de l'onduleur de tous les modules du SP1. Selon les connaissances dans le domaine, l'efficacité des onduleurs solaires devrait se situer entre 93 et ​​96 %. Étant donné que la plage d'efficacité de tous les modules est comprise entre 9,76 % et 9,79 %, cela illustre la nécessité d'étudier les performances de l'onduleur et de déterminer s'il doit être remplacé.

Étant donné que le SP1 a montré des problèmes avec l'onduleur, une analyse plus approfondie n'a été effectuée que sur le SP2.

Bien que cette brève analyse soit le résultat de plus de temps que nous avons passé à étudier l'onduleur, elle ne répond pas à la question principale de la détermination des performances du module solaire.

Étant donné que l’onduleur du SP2 fonctionne correctement, toute anomalie peut être identifiée et étudiée en approfondissant les données.

La figure 4 montre la relation entre la température du module et la température ambiante, et il existe des cas où la température du module est extrêmement élevée.

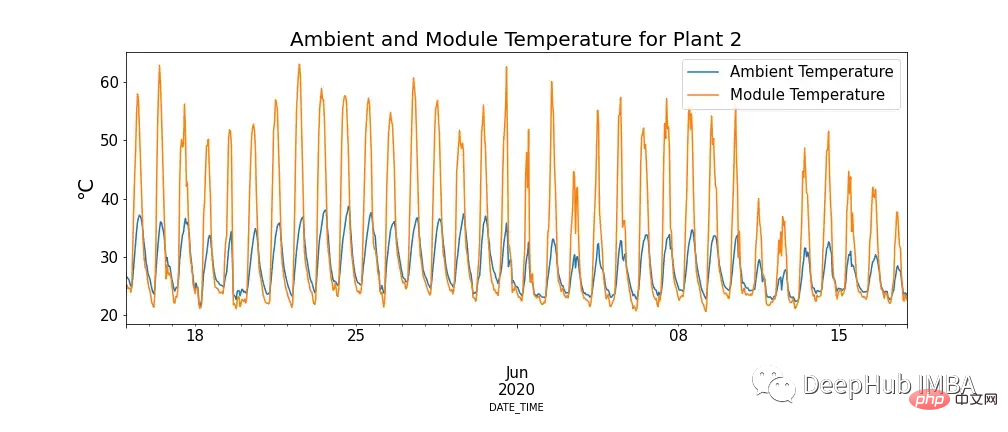
Cela peut sembler aller à l'encontre de nos connaissances, mais on constate que les températures élevées ont bel et bien un impact négatif sur les panneaux solaires. Lorsque les photons entrent en contact avec des électrons dans une cellule solaire, ils libèrent des électrons libres, mais à des températures plus élevées, davantage d'électrons sont déjà dans un état excité, ce qui réduit la tension que les panneaux peuvent produire, réduisant ainsi l'efficacité.

En tenant compte de ce phénomène, la figure 5 ci-dessous montre la température du module et la puissance CC pour le SP2 (les points de données où la température ambiante est inférieure à la température du module et les heures de la journée où le module fonctionne avec un nombre inférieur ont été filtrés pour éviter le biais des données).

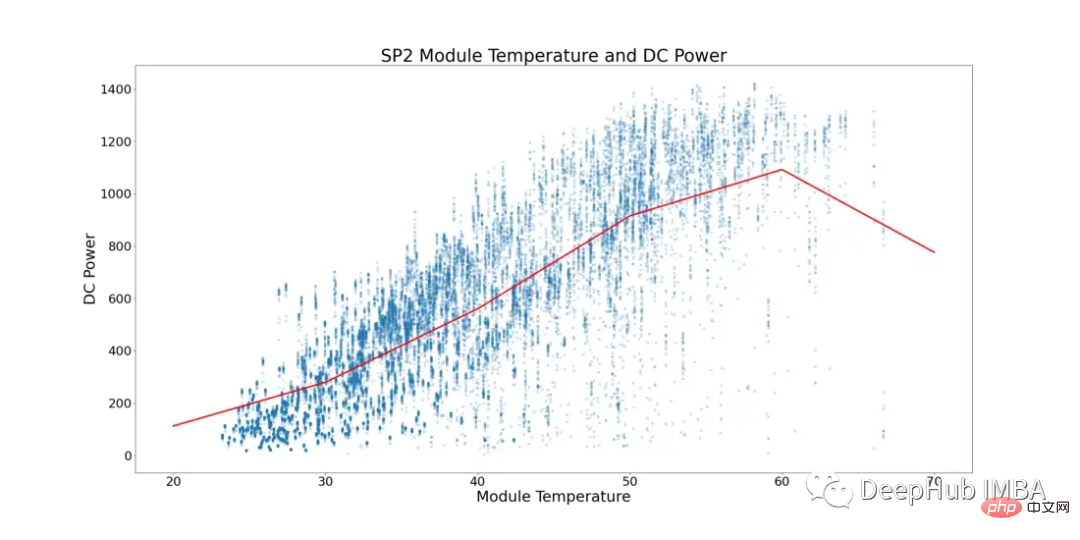
Dans la figure 5, la ligne rouge représente la température moyenne. Vous pouvez voir ici qu’il existe un point de basculement clair et des signes de stagnation de l’alimentation CC. Commence à atteindre un plateau à ~52°C. Afin de détecter les modules solaires aux performances sous-optimales, toutes les lignes affichant des températures de module supérieures à 52°C ont été supprimées.

La figure 6 ci-dessous montre la puissance CC de chaque module dans SP2 au cours d'une journée. Cela répond fondamentalement aux attentes et la production d'électricité est plus importante à midi. Mais il existe un autre problème : pendant les périodes de pointe, la production d’électricité est faible. Il nous est difficile de résumer les raisons de cette situation, car les conditions météorologiques peuvent être mauvaises ce jour-là, ou le SP2 peut nécessiter un entretien de routine, etc.

Il existe également des signes de modules à faible performance dans la figure 6. Ils peuvent être identifiés comme des modules (points de données individuels) sur le graphique qui s'écartent du cluster le plus proche.

Pour déterminer quels modules fonctionnent mal, nous pouvons effectuer des tests statistiques tout en comparant les performances de chaque module à d'autres modules pour déterminer les performances.

Toutes les 15 minutes, la distribution des alimentations CC de différents modules en même temps est une distribution normale grâce à des tests d'hypothèse, il peut être déterminé quels modules fonctionnent mal. Les comptes correspondent au nombre de fois qu'un module tombe en dehors de l'intervalle de confiance de 99,9 % avec une valeur p

La figure 7 montre par ordre décroissant le nombre de fois où chaque module a été statistiquement significativement inférieur aux autres modules au cours de la même période.

Il ressort clairement de la figure 7 que le module 'Quc1TzYxW2pYoWX' pose problème. Ces informations peuvent être fournies au personnel SP2 concerné pour enquêter sur la cause.

Modélisation

Ci-dessous, nous commençons la modélisation et la comparaison à l'aide de trois algorithmes de séries chronologiques différents : SARIMA, XGBoost et CNN-LSTM

Pour les trois modèles, prédisez le prochain point de données à l'aide de Predict. La validation progressive est une technique utilisée dans la modélisation de séries chronologiques, car les prédictions deviennent moins précises avec le temps. Une approche plus pratique consiste donc à recycler le modèle avec les données réelles lorsqu'elles deviennent disponibles.

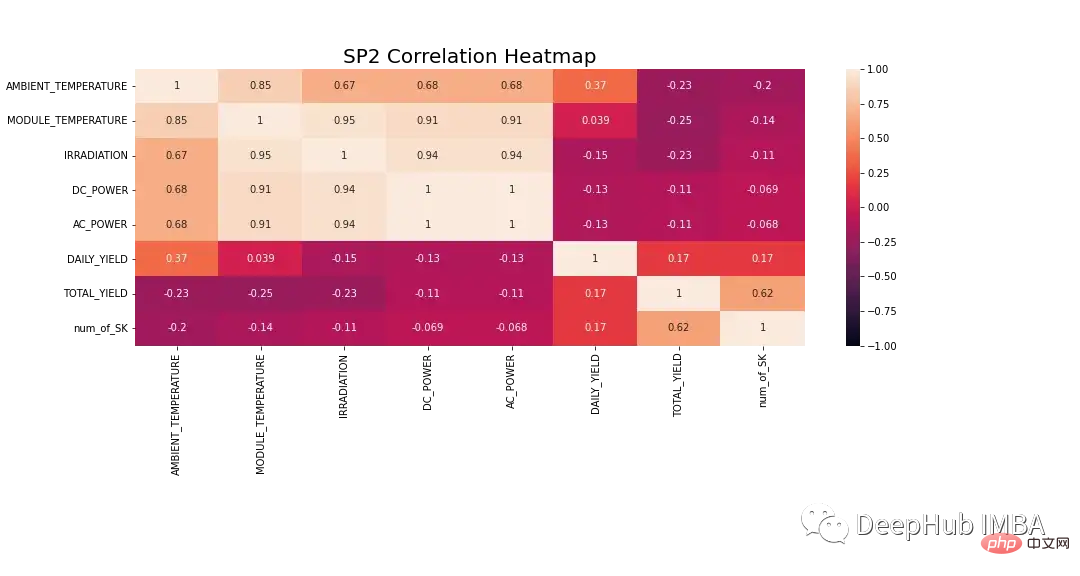
Les données doivent être étudiées plus en détail avant la modélisation. La figure 8 montre la carte thermique de corrélation pour toutes les fonctionnalités de l'ensemble de données SP2. La carte thermique montre la forte corrélation entre la variable dépendante, la puissance CC, avec la température du module, l'irradiation et la température ambiante. Ces caractéristiques peuvent jouer un rôle important dans la prédiction.

Dans la carte thermique ci-dessous, le courant alternatif affiche un coefficient de corrélation de Pearson de 1. Pour éviter les problèmes de fuite de données, nous supprimons l'alimentation CC des données.

SARIMA

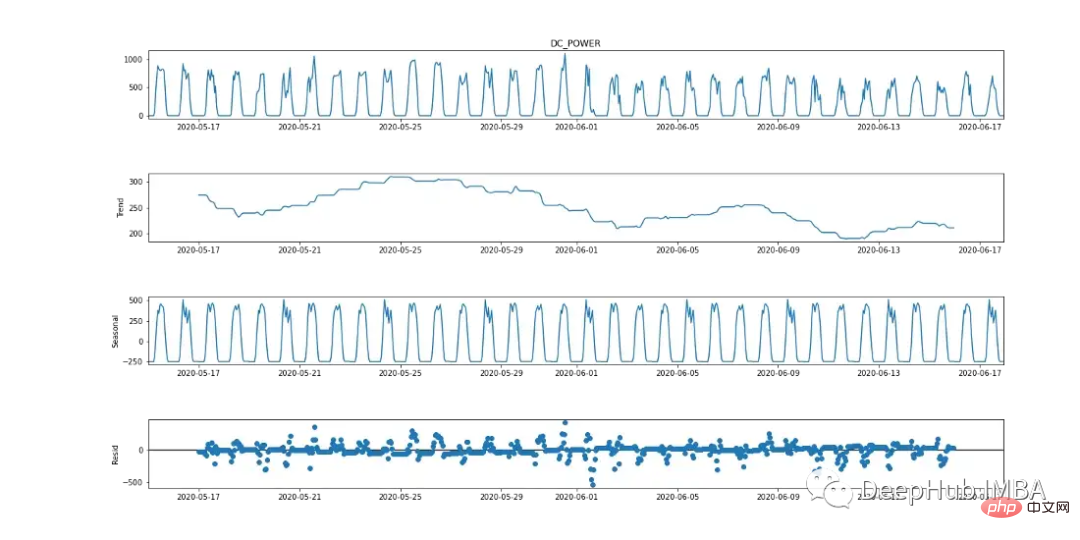
La moyenne mobile intégrée autorégressive saisonnière (SARIMA) est une méthode de prévision de séries chronologiques univariées. Étant donné que la variable cible montre des signes d'une période cyclique de 24 heures, SARIMA est une option de modélisation efficace car elle prend en compte les effets saisonniers. Cela peut être observé dans le tableau de répartition saisonnière ci-dessous.

L'algorithme SARIMA nécessite que les données soient stationnaires. Il existe différentes manières de tester si les données sont stationnaires, telles que les tests statistiques (test de Dickey-Fowler augmenté), les statistiques récapitulatives (comparaison des moyennes/variances de différentes parties des données) et l'analyse visuelle des données. Il est important d'effectuer plusieurs tests avant la modélisation.

Le test Augmented Dickey-Fuller (ADF) est un « test de racine unitaire » utilisé pour déterminer si une série chronologique est stationnaire. Fondamentalement, il s'agit d'un test de signification statistique dans lequel il existe une hypothèse nulle et une hypothèse alternative et une conclusion est tirée sur la base de la valeur p résultante.

Hypothèse nulle : les données des séries chronologiques sont non stationnaires.

Hypothèse alternative : les données des séries chronologiques sont stationnaires.

Dans notre exemple, si la valeur p ≤ 0,05, nous pouvons rejeter l'hypothèse nulle et confirmer que les données n'ont pas de racine unitaire.

 from statsmodels.tsa.stattools import adfuller
 
 result = adfuller(plant2_dcpower.values)
 
 print('ADF Statistic: %f' % result[0])
 print('p-value: %f' % result[1])
 print('Critical Values:')
 for key, value in result[4].items():
print('t%s: %.3f' % (key, value))

D'après le test ADF, la valeur p est de 0,000553,

Afin de modéliser la variable dépendante avec SARIMA, la série chronologique doit être stationnaire. Comme le montre la figure 9 (premier et troisième graphiques), DC présente des signes évidents de saisonnalité. Prenez la première différence [t-(t-1)] pour supprimer la composante saisonnière, comme le montre la figure 10, car elle ressemble à une distribution normale. Les données sont désormais stationnaires et adaptées à l'algorithme SARIMA. Les hyperparamètres de

SARIMA incluent p (ordre autorégressif), d (ordre de différence), q (ordre de moyenne mobile), p (ordre autorégressif saisonnier), d (ordre de différence saisonnière), q (ordre de moyenne mobile saisonnière), m (pas de temps du cycle saisonnier), tendance (tendance déterministe).

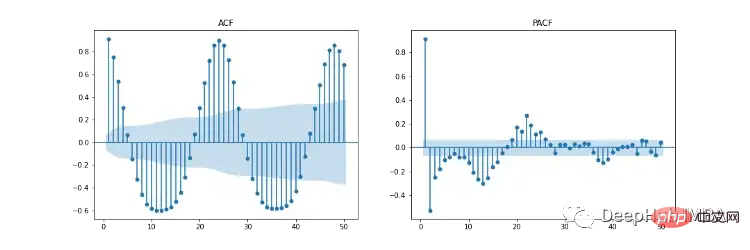
La figure 11 montre les tracés d'autocorrélation (ACF), d'autocorrélation partielle (PACF) et d'ACF/PACF saisonniers. Le tracé ACF montre la corrélation entre une série chronologique et sa version retardée. PACF montre une corrélation directe entre une série chronologique et sa version décalée. La zone ombrée en bleu représente l'intervalle de confiance. SACF et SPACF peuvent être calculés en prenant la différence saisonnière (m) des données originales, dans ce cas 24, car il existe un effet saisonnier évident sur 24 heures dans le graphique ACF.

Selon notre intuition, le point de départ des hyperparamètres peut être dérivé des tracés ACF et PACF. Par exemple, ACF et PACF affichent une tendance à la baisse progressive, c'est-à-dire que l'ordre autorégressif (p) et l'ordre moyen mobile (q) sont tous deux supérieurs à 0. p et p peuvent être déterminés en examinant respectivement les tracés PCF et SPCF et en comptant le nombre de décalages qui deviennent statistiquement significatifs avant que la valeur du décalage ne devienne insignifiante. De même, q et q peuvent être trouvés dans les diagrammes ACF et SACF.

L'ordre des différences (d) peut être déterminé par le nombre de différences qui rendent les données stationnaires. L'ordre des différences saisonnières (D) est estimé à partir du nombre de différences nécessaires pour supprimer la composante saisonnière de la série chronologique.

Vous pouvez lire cet article pour ces sélections d'hyperparamètres : https://arauto.readthedocs.io/en/latest/how_to_choose_terms.html

Vous pouvez également utiliser la méthode de recherche de grille pour l'optimisation des hyperparamètres, basée sur l'erreur quadratique moyenne minimale (MSE) ) Sélectionnez les hyperparamètres optimaux, notamment p = 2, d = 0, q = 4, p = 2, d = 1, q = 6, m = 24, tendance = 'n' (pas de tendance).

from time import time
 from sklearn.metrics import mean_squared_error
 from statsmodels.tsa.statespace.sarimax import SARIMAX
 
 configg = [(2, 1, 4), (2, 1, 6, 24), 'n']
 
 def train_test_split(data, test_len=48):
"""
Split data into training and testing.
"""
train, test = data[:-test_len], data[-test_len:]
return train, test
 
 def sarima_model(data, cfg, test_len, i):
"""
SARIMA model which outputs prediction and model.
"""
order, s_order, t = cfg[0], cfg[1], cfg[2]
model = SARIMAX(data, order=order, seasonal_order=s_order, trend=t,
enforce_stationarity=False, enfore_invertibility=False)
model_fit = model.fit(disp=False)
yhat = model_fit.predict(len(data))
 
if i + 1 == test_len:
return yhat, model_fit
else:
return yhat
 
 def walk_forward_val(data, cfg):
"""
A walk forward validation technique used for time series data. Takes current value of x_test and predicts
value. x_test is then fed back into history for the next prediction.
"""
train, test = train_test_split(data)
pred = []
history = [i for i in train]
test_len = len(test)
 
for i in range(test_len):
if i + 1 == test_len:
yhat, s_model = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
mse = mean_squared_error(test, pred)
return pred, mse, s_model
else:
yhat = sarima_model(history, cfg, test_len, i)
pred.append(yhat)
history.append(test[i])
pass
 
 if __name__ == '__main__':
start_time = time()
sarima_pred_plant2, sarima_mse, s_model = walk_forward_val(plant2_dcpower, configg)
time_len = time() - start_time
 
print(f'SARIMA runtime: {round(time_len/60,2)} mins')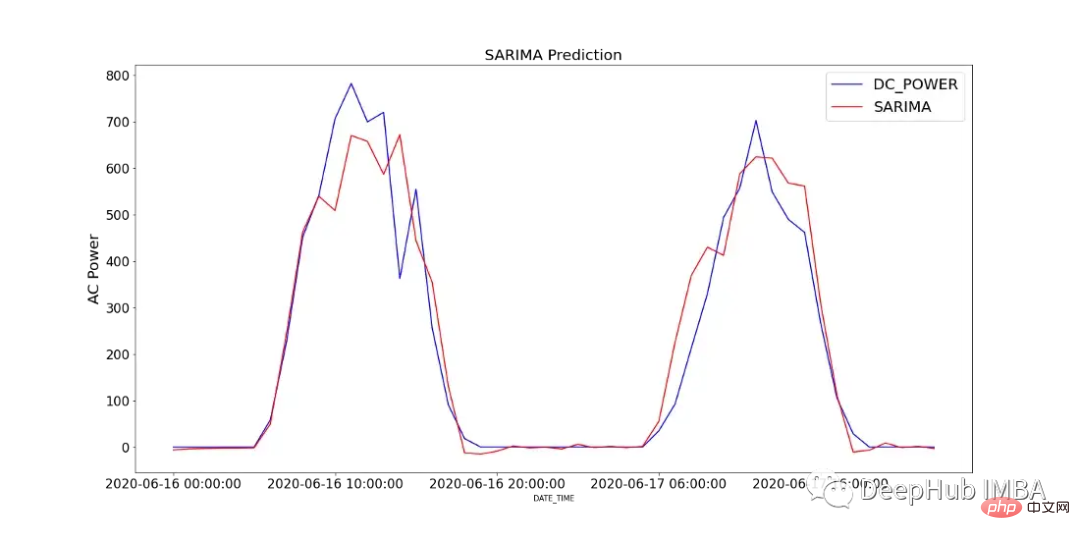

La figure 12 montre la comparaison des valeurs prédites du modèle SARIMA avec la puissance DC enregistrée sur 2 jours dans SP2.

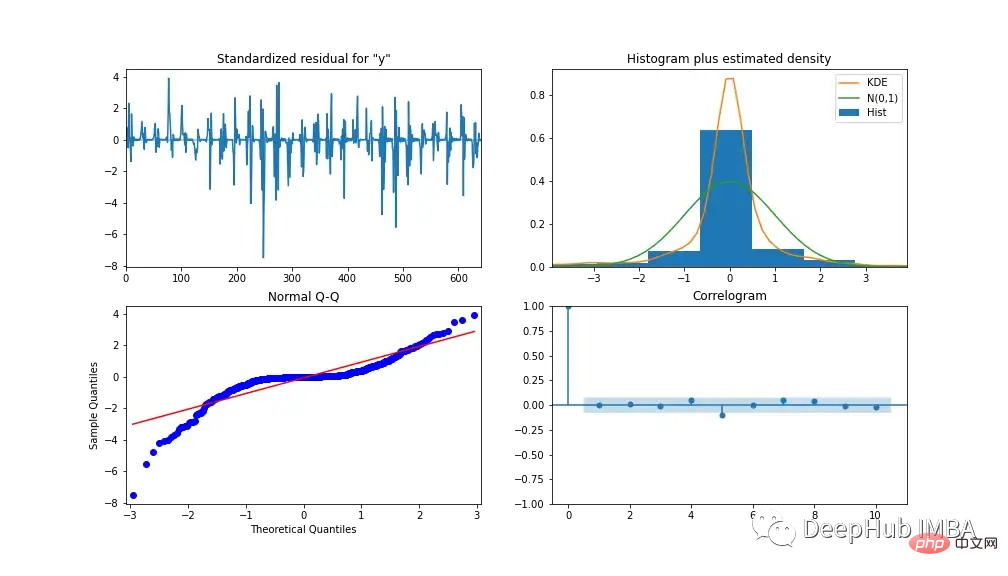
Pour analyser les performances du modèle, la figure 13 montre les diagnostics du modèle. Le tracé de corrélation ne montre presque aucune corrélation après le premier décalage et l'histogramme ci-dessous montre une distribution normale autour de la moyenne de zéro. De là, nous pouvons dire que le modèle ne peut pas tirer davantage d’informations des données.

XGBoost

XGBoost (eXtreme Gradient Boosting) est un algorithme d'arbre de décision améliorant le gradient. Il utilise une approche d'ensemble dans laquelle de nouveaux modèles d'arbre de décision sont ajoutés pour modifier les scores des arbres de décision existants. Contrairement à SARIMA, XGBoost est un algorithme d'apprentissage automatique multivarié, ce qui signifie que le modèle peut adopter plusieurs fonctionnalités pour améliorer ses performances.

Nous utilisons l'ingénierie des fonctionnalités pour améliorer la précision du modèle. 3 caractéristiques supplémentaires ont également été créées, qui incluent des versions retardées de l'alimentation CA et CC, S1_AC_POWER et S1_DC_POWER respectivement, et l'efficacité globale EFF, qui est la puissance CA divisée par la puissance CC. Et supprimez AC_POWER et MODULE_TEMPERATURE des données. La figure 14 montre le niveau d'importance des fonctionnalités par gain (gain moyen de fractionnement à l'aide d'une fonctionnalité) et par poids (nombre de fois qu'une fonctionnalité apparaît dans l'arborescence).

Déterminez les hyperparamètres utilisés dans la modélisation grâce à la recherche par grille. Les résultats sont : *taux d'apprentissage = 0,01, nombre d'estimateurs = 1200, sous-échantillon = 0,8, échantillon par arbre = 1, échantillon par niveau = 1, poids min de l'enfant. = 20 et profondeur maximale = 10

Nous utilisons MinMaxScaler pour mettre à l'échelle les données d'entraînement entre 0 et 1 (vous pouvez également expérimenter avec d'autres scalers tels que la transformation logarithmique et le scaler standard, en fonction de la distribution des données). Convertissez les données en un ensemble de données d'apprentissage supervisé en reculant toutes les variables indépendantes d'un certain laps de temps.

 import numpy as np
 import pandas as pd
 import xgboost as xgb
 from sklearn.preprocessing import MinMaxScaler
 from time import time
 
 def train_test_split(df, test_len=48):
"""
split data into training and testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def data_to_supervised(df, shift_by=1, target_var='DC_POWER'):
"""
Convert data into a supervised learning problem.
"""
target = df[target_var][shift_by:].values
dep = df.drop(target_var, axis=1).shift(-shift_by).dropna().values
data = np.column_stack((dep, target))
return data
 
 
 def xgb_forecast(train, x_test):
"""
XGBOOST model which outputs prediction and model.
"""
x_train, y_train = train[:,:-1], train[:,-1]
xgb_model = xgb.XGBRegressor(learning_rate=0.01, n_estimators=1500, subsample=0.8,
colsample_bytree=1, colsample_bylevel=1,
min_child_weight=20, max_depth=14, objective='reg:squarederror')
xgb_model.fit(x_train, y_train)
yhat = xgb_model.predict([x_test])
return yhat[0], xgb_model
 
 def walk_forward_validation(df):
"""
A walk forward validation approach by scaling the data and changing into a supervised learning problem.
"""
preds = []
train, test = train_test_split(df)
 
scaler = MinMaxScaler(feature_range=(0,1))
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)
 
train_scaled_df = pd.DataFrame(train_scaled, columns = train.columns, index=train.index)
test_scaled_df = pd.DataFrame(test_scaled, columns = test.columns, index=test.index)
 
train_scaled_sup, test_scaled_sup = data_to_supervised(train_scaled_df), data_to_supervised(test_scaled_df)
history = np.array([x for x in train_scaled_sup])
 
for i in range(len(test_scaled_sup)):
test_x, test_y = test_scaled_sup[i][:-1], test_scaled_sup[i][-1]
yhat, xgb_model = xgb_forecast(history, test_x)
preds.append(yhat)
np.append(history,[test_scaled_sup[i]], axis=0)
 
pred_array = test_scaled_df.drop("DC_POWER", axis=1).to_numpy()
pred_num = np.array([pred])
pred_array = np.concatenate((pred_array, pred_num.T), axis=1)
result = scaler.inverse_transform(pred_array)
 
return result, test, xgb_model
 
 if __name__ == '__main__':
start_time = time()
xgb_pred, actual, xgb_model = walk_forward_validation(dropped_df_cat)
time_len = time() - start_time
 
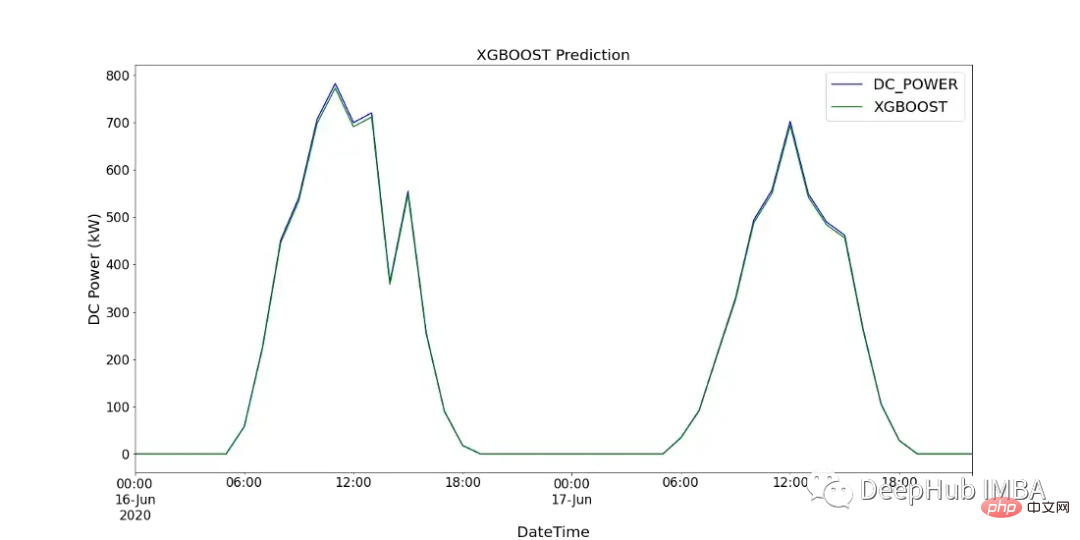
print(f'XGBOOST runtime: {round(time_len/60,2)} mins')

图15显示了XGBoost模型的预测值与SP2 2天内记录的直流功率的比较。

CNN-LSTM

CNN-LSTM (convolutional Neural Network Long - Short-Term Memory)是两种神经网络模型的混合模型。CNN是一种前馈神经网络，在图像处理和自然语言处理方面表现出了良好的性能。它还可以有效地应用于时间序列数据的预测。LSTM是一种序列到序列的神经网络模型，旨在解决长期存在的梯度爆炸/消失问题，使用内部存储系统，允许它在输入序列上积累状态。

在本例中，使用CNN-LSTM作为编码器-解码器体系结构。由于CNN不直接支持序列输入，所以我们通过1D CNN读取序列输入并自动学习重要特征。然后LSTM进行解码。与XGBoost模型类似，使用scikitlearn的MinMaxScaler使用相同的数据并进行缩放，但范围在-1到1之间。对于CNN-LSTM，需要将数据重新整理为所需的结构:[samples, subsequences, timesteps, features]，以便可以将其作为输入传递给模型。

由于我们希望为每个子序列重用相同的CNN模型，因此使用timedidistributedwrapper对每个输入子序列应用一次整个模型。在下面的图16中可以看到最终模型中使用的不同层的模型摘要。

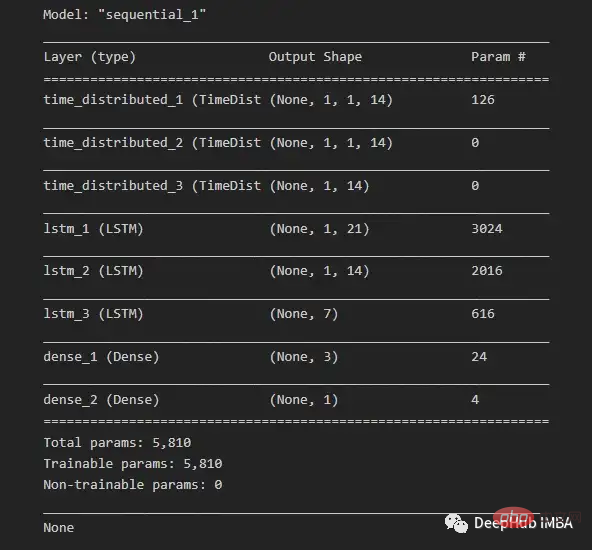
在将数据分解为训练数据和测试数据之后，将训练数据分解为训练数据和验证数据集。在所有训练数据(包括验证数据)的每次迭代之后，模型可以进一步使用这一点来评估模型的性能。

学习曲线是深度学习中使用的一个很好的诊断工具，它显示了模型在每个阶段之后的表现。下面的图17显示了模型如何从数据中学习，并显示了验证数据与训练数据的收敛。这是良好模特训练的标志。

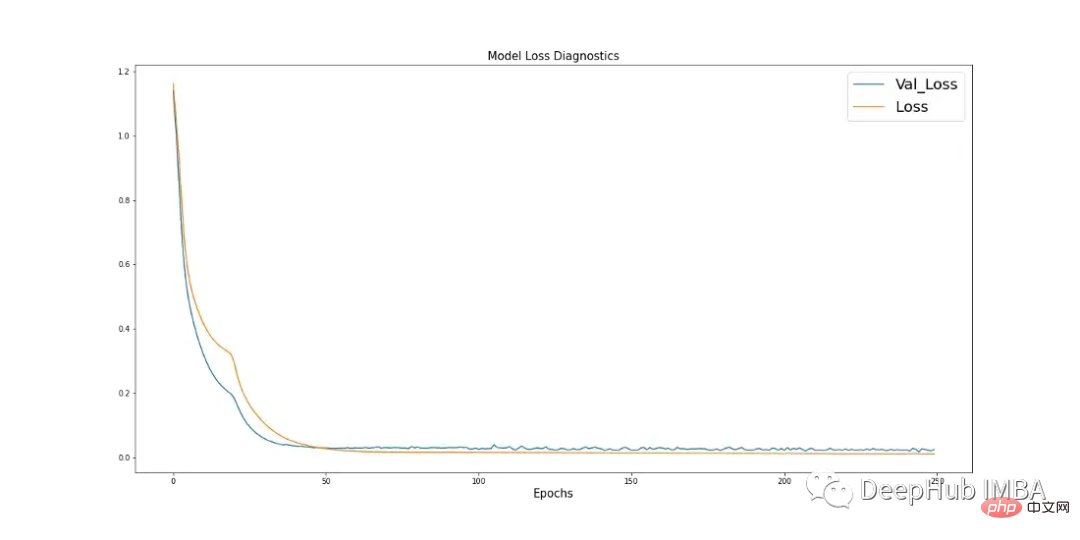
import pandas as pd
 import numpy as np
 from sklearn.metrics import mean_squared_error
 from sklearn.preprocessing import MinMaxScaler
 import keras
 from keras.models import Sequential
 from keras.layers.convolutional import Conv1D, MaxPooling1D
 from keras.layers import LSTM, TimeDistributed, RepeatVector, Dense, Flatten
 from keras.optimizers import Adam
 
 n_steps = 1
 subseq = 1
 
 def train_test_split(df, test_len=48):
"""
Split data in training and testing. Use 48 hours as testing.
"""
train, test = df[:-test_len], df[-test_len:]
return train, test
 
 def split_data(sequences, n_steps):
"""
Preprocess data returning two arrays.
"""
x, y = [], []
for i in range(len(sequences)):
end_x = i + n_steps
 
if end_x > len(sequences):
break
x.append(sequences[i:end_x, :-1])
y.append(sequences[end_x-1, -1])
 
return np.array(x), np.array(y)
 
def CNN_LSTM(x, y, x_val, y_val):
"""
CNN-LSTM model.
"""
model = Sequential()
model.add(TimeDistributed(Conv1D(filters=14, kernel_size=1, activation="sigmoid",
input_shape=(None, x.shape[2], x.shape[3]))))
model.add(TimeDistributed(MaxPooling1D(pool_size=1)))
model.add(TimeDistributed(Flatten()))
model.add(LSTM(21, activation="tanh", return_sequences=True))
model.add(LSTM(14, activation="tanh", return_sequences=True))
model.add(LSTM(7, activation="tanh"))
model.add(Dense(3, activation="sigmoid"))
model.add(Dense(1))
 
model.compile(optimizer=Adam(learning_rate=0.001), loss="mse", metrics=['mse'])
history = model.fit(x, y, epochs=250, batch_size=36,
verbose=0, validation_data=(x_val, y_val))
 
return model, history
 
 # split and resahpe data
 train, test = train_test_split(dropped_df_cat)
 
 train_x = train.drop(columns="DC_POWER", axis=1).to_numpy()
 train_y = train["DC_POWER"].to_numpy().reshape(len(train), 1)
 
 test_x = test.drop(columns="DC_POWER", axis=1).to_numpy()
 test_y = test["DC_POWER"].to_numpy().reshape(len(test), 1)
 
 #scale data
 scaler_x = MinMaxScaler(feature_range=(-1,1))
 scaler_y = MinMaxScaler(feature_range=(-1,1))
 
 train_x = scaler_x.fit_transform(train_x)
 train_y = scaler_y.fit_transform(train_y)
 
 test_x = scaler_x.transform(test_x)
 test_y = scaler_y.transform(test_y)
 
 
 # shape data into CNN-LSTM format [samples, subsequences, timesteps, features] ORIGINAL
 train_data_np = np.hstack((train_x, train_y))
 x, y = split_data(train_data_np, n_steps)
 x_subseq = x.reshape(x.shape[0], subseq, x.shape[1], x.shape[2])
 
 # create validation set
 x_val, y_val = x_subseq[-24:], y[-24:]
 x_train, y_train = x_subseq[:-24], y[:-24]
 
 n_features = x.shape[2]
 actual = scaler_y.inverse_transform(test_y)
 
 # run CNN-LSTM model
 if __name__ == '__main__':
start_time = time()
 
model, history = CNN_LSTM(x_train, y_train, x_val, y_val)
prediction = []
 
for i in range(len(test_x)):
test_input = test_x[i].reshape(1, subseq, n_steps, n_features)
yhat = model.predict(test_input, verbose=0)
yhat_IT = scaler_y.inverse_transform(yhat)
prediction.append(yhat_IT[0][0])
 
time_len = time() - start_time
mse = mean_squared_error(actual.flatten(), prediction)
 
print(f'CNN-LSTM runtime: {round(time_len/60,2)} mins')
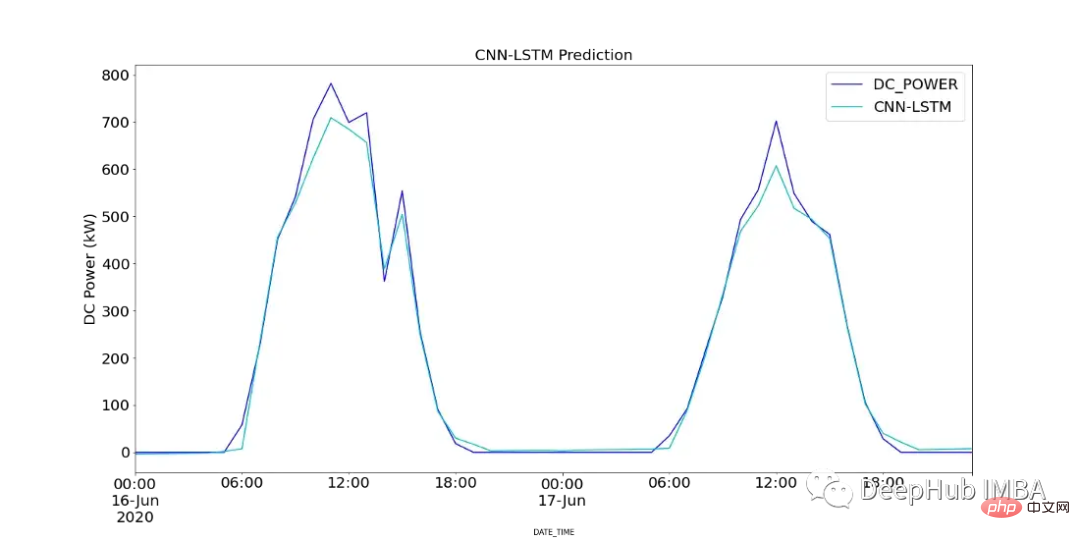
print(f"CNN-LSTM MSE: {round(mse,2)}")

图18显示了CNN-LSTM模型的预测值与SP2 2天内记录的直流功率的对比。

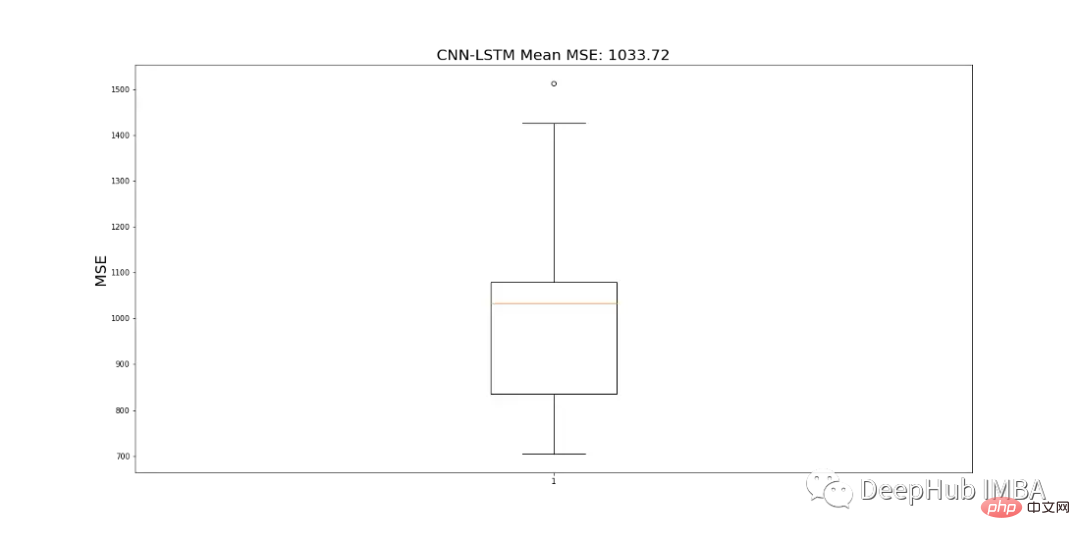
由于CNN-LSTM的随机性，该模型运行10次，并记录一个平均MSE值作为最终值，以判断模型的性能。图19显示了为所有模型运行记录的mse的范围。

结果对比

下表显示了每个模型的MSE (CNN-LSTM的平均MSE)和每个模型的运行时间(以分钟为单位)。

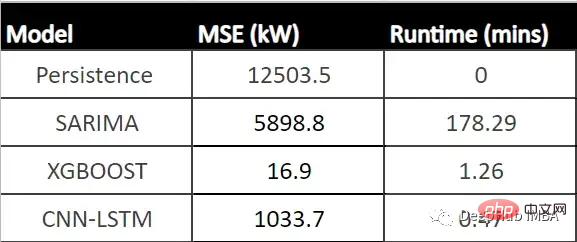
从表中可以看出，XGBoost的MSE最低、运行时第二快，并且与所有其他模型相比具有最佳性能。由于该模型显示了一个可以接受的每小时预测的运行时，它可以成为帮助运营经理决策过程的强大工具。

总结

在本文中我们分析了SP1和SP2，确定SP1性能较低。所以对SP2的进一步调查显示，并且查看了SP2中那些模块性能可能有问题，并使用假设检验来计算每个模块在统计上明显表现不佳的次数，' Quc1TzYxW2pYoWX '模块显示了约850次低性能计数。

我们使用数据训练三个模型：SARIMA、XGBoost和CNN-LSTM。SARIMA表现最差，XGBOOST表现最好，MSE为16.9，运行时间为1.43 min。所以可以说XGBoost在表格数据中还是最优先得选择。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!