Maison >Périphériques technologiques >IA >Comparaison des technologies courantes de réduction de dimensionnalité : analyse de faisabilité de la réduction des dimensions des données tout en préservant l'intégrité des informations
Comparaison des technologies courantes de réduction de dimensionnalité : analyse de faisabilité de la réduction des dimensions des données tout en préservant l'intégrité des informations
- 王林avant
- 2023-04-23 18:46:081387parcourir
Cet article comparera l'efficacité de diverses techniques de réduction de dimensionnalité sur des données tabulaires dans des tâches d'apprentissage automatique. Nous appliquons des méthodes de réduction de dimensionnalité à l'ensemble de données et évaluons leur efficacité au moyen d'analyses de régression et de classification. Nous appliquons des méthodes de réduction de dimensionnalité à divers ensembles de données obtenus à partir d'UCI liés à différents domaines. Au total, 15 ensembles de données ont été sélectionnés, dont 7 seront utilisés pour la régression et 8 pour la classification.
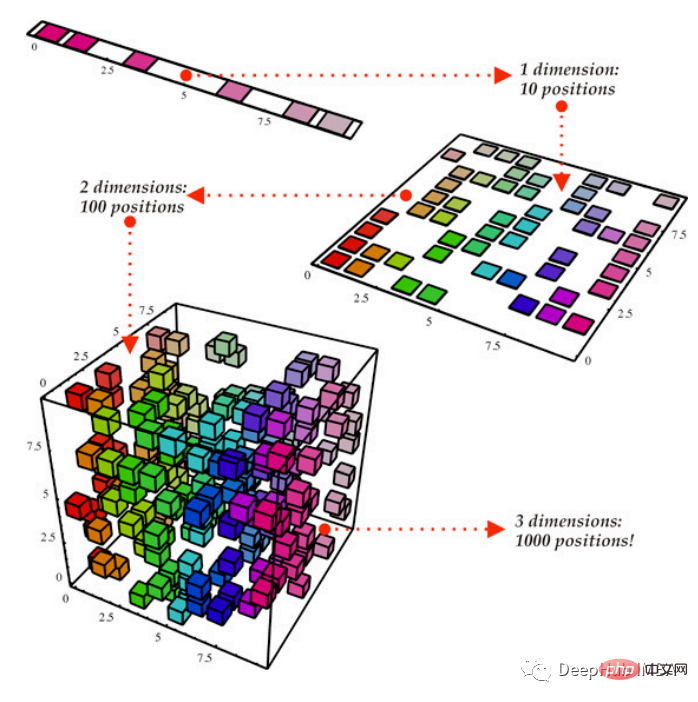
Pour rendre cet article facile à lire et à comprendre, seuls le prétraitement et l'analyse d'un ensemble de données sont présentés. L'expérience commence par le chargement de l'ensemble de données. L'ensemble de données est divisé en ensembles d'entraînement et de test, puis normalisé pour avoir une moyenne de 0 et un écart type de 1.
Des techniques de réduction de dimensionnalité sont ensuite appliquées aux données d'entraînement et l'ensemble de test est transformé pour une réduction de dimensionnalité en utilisant les mêmes paramètres. Pour la régression, l'analyse en composantes principales (ACP) et la décomposition en valeurs singulières (SVD) sont utilisées pour la réduction de la dimensionnalité. D'autre part, pour la classification, l'analyse discriminante linéaire (LDA) est utilisée. Après la réduction de la dimensionnalité, plusieurs modèles d'apprentissage automatique sont formés. tests, et les performances de différents modèles sur différents ensembles de données obtenus par différentes méthodes de réduction de dimensionnalité ont été comparées.
Traitement des données
import pandas as pd ## for data manipulation df = pd.read_excel(r'RegressionAirQualityUCI.xlsx') print(df.shape) df.head()
 L'ensemble de données contient 15 colonnes, dont une est nécessaire pour prédire l'étiquette. Avant de poursuivre la réduction de dimensionnalité, les colonnes de date et d'heure sont également supprimées.
L'ensemble de données contient 15 colonnes, dont une est nécessaire pour prédire l'étiquette. Avant de poursuivre la réduction de dimensionnalité, les colonnes de date et d'heure sont également supprimées.
X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1) y = df['CO(GT)'] X.shape, y.shape #Output: ((9357, 12), (9357,))
Pour la formation, nous devons partitionner l'ensemble de données en un ensemble d'entraînement et un ensemble de test, afin que l'efficacité de la méthode de réduction de dimensionnalité et du modèle d'apprentissage automatique formé sur l'espace des fonctionnalités de réduction de dimensionnalité puisse être évaluée. Le modèle sera formé à l'aide de l'ensemble de formation et les performances seront évaluées à l'aide de l'ensemble de test.
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) X_train.shape, X_test.shape, y_train.shape, y_test.shape #Output: ((7485, 12), (1872, 12), (7485,), (1872,))
Avant d'utiliser des techniques de réduction de dimensionnalité sur l'ensemble de données, les données d'entrée peuvent être mises à l'échelle pour garantir que toutes les entités sont à la même échelle. Ceci est crucial pour les modèles linéaires, car certaines méthodes de réduction de dimensionnalité peuvent modifier leur résultat selon que les données sont normalisées ou non et sont sensibles à la taille des caractéristiques.
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) X_train.shape, X_test.shape
Analyse en composantes principales (ACP)
La méthode PCA de réduction de dimensionnalité linéaire réduit la dimensionnalité des données tout en conservant autant de variance des données que possible.
La méthode PCA du module Python sklearn.decomposition sera utilisée ici. Le nombre de composants à conserver est spécifié via ce paramètre, et ce nombre affecte le nombre de dimensions incluses dans le plus petit espace de fonctionnalités. Comme alternative, nous pouvons définir une variance cible à conserver, qui établit le nombre de composants en fonction de la quantité de variance dans les données capturées, que nous définissons ici à 0,95
from sklearn.decomposition import PCA pca = PCA(n_compnotallow=0.95) X_train_pca = pca.fit_transform(X_train) X_test_pca = pca.transform(X_test) X_train_pca
 Que représentent les caractéristiques ci-dessus ? L'analyse des composants (ACP) projette les données dans un espace de faible dimension, en essayant de préserver autant de différences que possible dans les données. Même si cela peut faciliter des opérations spécifiques, cela peut également rendre les données plus difficiles à comprendre. , PCA peut identifier de nouveaux axes dans les données qui sont des fusions linéaires des caractéristiques initiales.
Que représentent les caractéristiques ci-dessus ? L'analyse des composants (ACP) projette les données dans un espace de faible dimension, en essayant de préserver autant de différences que possible dans les données. Même si cela peut faciliter des opérations spécifiques, cela peut également rendre les données plus difficiles à comprendre. , PCA peut identifier de nouveaux axes dans les données qui sont des fusions linéaires des caractéristiques initiales.
Décomposition en valeurs singulières (SVD)
SVD est une technique de réduction de dimensionnalité linéaire qui projette des caractéristiques avec une faible variance de données dans un espace de faible dimension. Nous devons définir le nombre de composants à conserver après la réduction de dimensionnalité. Ici, nous allons réduire la dimensionnalité de 2/3.
from sklearn.decomposition import TruncatedSVD svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33)) X_train_svd = svd.fit_transform(X_train) X_test_svd = svd.transform(X_test) X_train_svd
 Formation du modèle de régression
Formation du modèle de régression
Maintenant, nous allons commencer à former et tester le modèle en utilisant les trois types de données ci-dessus (ensemble de données d'origine, PCA et SVD), et nous utilisons plusieurs modèles à des fins de comparaison.
import numpy as np from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import SVR from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor from sklearn.metrics import r2_score, mean_squared_error import time
train_test_ML : Cette fonction complétera les tâches répétitives liées à la formation et aux tests du modèle. Les performances de tous les modèles ont été évaluées en calculant rmse et r2_score. et renvoie un ensemble de données avec tous les détails et les valeurs calculées. Il enregistrera également le temps nécessaire à chaque modèle pour s'entraîner et tester sur son ensemble de données respectif.
def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
r2 = np.round(r2_score(y_test, y_pred), 2)
rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
return temp_dfDonnées originales :
original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df
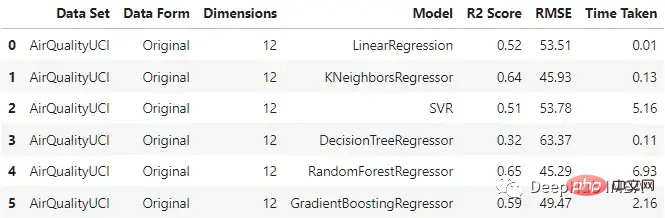 On peut voir que le régresseur KNN et la forêt aléatoire fonctionnent relativement bien lors de la saisie des données originales, et le temps de formation de la forêt aléatoire est le plus long.
On peut voir que le régresseur KNN et la forêt aléatoire fonctionnent relativement bien lors de la saisie des données originales, et le temps de formation de la forêt aléatoire est le plus long.
PCA
pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test)
pca_df
与原始数据集相比,不同模型的性能有不同程度的下降。梯度增强回归和支持向量回归在两种情况下保持了一致性。这里一个主要的差异也是预期的是模型训练所花费的时间。与其他模型不同的是,SVR在这两种情况下花费的时间差不多。
SVD
svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df
与PCA相比,SVD以更大的比例降低了维度,随机森林和梯度增强回归器的表现相对优于其他模型。
回归模型分析
对于这个数据集,使用主成分分析时,数据维数从12维降至5维,使用奇异值分析时,数据降至3维。
- 就机器学习性能而言,数据集的原始形式相对更好。造成这种情况的一个潜在原因可能是,当我们使用这种技术降低维数时,在这个过程中会发生信息损失。
- 但是线性回归、支持向量回归和梯度增强回归在原始和PCA案例中的表现是一致的。
- 在我们通过SVD得到的数据上,所有模型的性能都下降了。
- 在降维情况下,由于特征变量的维数较低,模型所花费的时间减少了。
将类似的过程应用于其他六个数据集进行测试,得到以下结果:
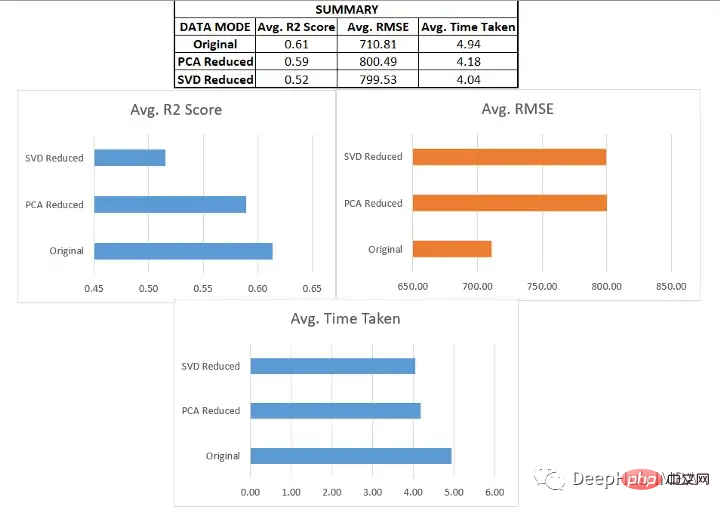
我们在各种数据集上使用了SVD和PCA,并对比了在原始高维特征空间上训练的回归模型与在约简特征空间上训练的模型的有效性
- 原始数据集始终优于由降维方法创建的低维数据。这说明在降维过程中可能丢失了一些信息。
- 当用于更大的数据集时,降维方法有助于显著减少数据集中的特征数量,从而提高机器学习模型的有效性。对于较小的数据集,改影响并不显著。
- 模型的性能在original和pca_reduced两种模式下保持一致。如果一个模型在原始数据集上表现得更好,那么它在PCA模式下也会表现得更好。同样,较差的模型也没有得到改进。
- 在SVD的情况下,模型的性能下降比较明显。这可能是n_components数量选择的问题,因为太小数量肯定会丢失数据。
- 决策树在SVD数据集时一直是非常差的,因为它本来就是一个弱学习器
训练分类模型
对于分类我们将使用另一种降维方法:LDA。机器学习和模式识别任务经常使用被称为线性判别分析(LDA)的降维方法。这种监督学习技术旨在最大化几个类或类别之间的距离,同时将数据投影到低维空间。由于它的作用是最大化类之间的差异,因此只能用于分类任务。
from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score
继续我们的训练方法
def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
start_time = time.time()
reg = i().fit(X_train, y_train)
y_pred = reg.predict(X_test)
accuracy = np.round(accuracy_score(y_test, y_pred), 2)
f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
end_time = time.time()
time_taken = np.round((end_time - start_time), 2)
temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
return temp_df开始训练
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda = LinearDiscriminantAnalysis() X_train_lda = lda.fit_transform(X_train, y_train) X_test_lda = lda.transform(X_test)
预处理、分割和数据集的缩放,都与回归部分相同。在对8个不同的数据集进行新联后我们得到了下面结果:
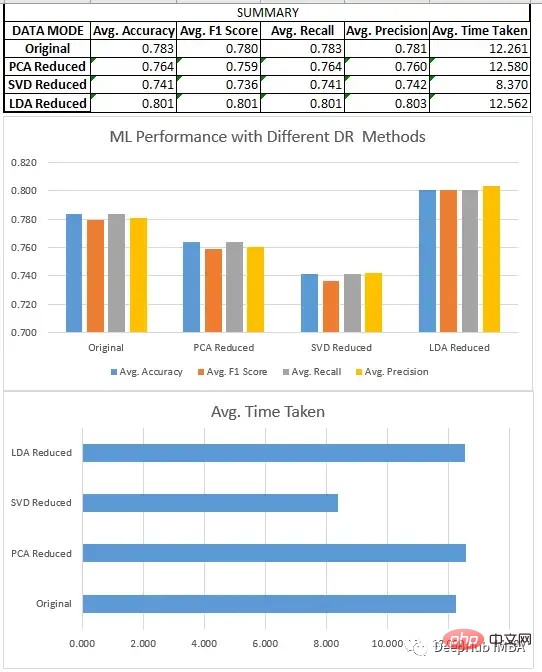
分类模型分析
我们比较了上面所有的三种方法SVD、LDA和PCA。
- LDA数据集通常优于原始形式的数据和由其他降维方法创建的低维数据,因为它旨在识别最有效区分类的特征的线性组合,而原始数据和其他无监督降维技术不关心数据集的标签。
- 降维技术在应用于更大的数据集时,可以极大地减少了数据集中的特征数量,这提高了机器学习模型的效率。在较小的数据集上,影响不是特别明显。除了LDA(它在这些情况下也很有效),因为它们在一些情况下,如二元分类,可以将数据集的维度减少到只有一个。
- 当我们在寻找一定的性能时,LDA可以是分类问题的一个非常好的起点。
- SVD与回归一样,模型的性能下降很明显。需要调整n_components的选择。
总结
我们比较了一些降维技术的性能,如奇异值分解(SVD)、主成分分析(PCA)和线性判别分析(LDA)。我们的研究结果表明,方法的选择取决于特定的数据集和手头的任务。
Pour les tâches de régression, nous constatons que PCA est généralement plus performant que SVD. Dans le cas de la classification, LDA surpasse SVD et PCA, ainsi que l'ensemble de données d'origine. Il est important que l'analyse discriminante linéaire (LDA) bat systématiquement l'analyse en composantes principales (ACP) dans les tâches de classification, mais cela ne signifie pas que l'ADL est une meilleure technique en général. En effet, LDA est un algorithme d'apprentissage supervisé qui s'appuie sur des données étiquetées pour localiser les caractéristiques les plus discriminantes des données, tandis que PCA est une technique non supervisée qui ne nécessite pas de données étiquetées et cherche à maintenir autant de variance que possible. Par conséquent, la PCA peut être mieux adaptée aux tâches non supervisées ou aux situations où l’interprétabilité est critique, tandis que la LDA peut être mieux adaptée aux tâches impliquant des données étiquetées.
Bien que les techniques de réduction de dimensionnalité puissent aider à réduire le nombre de fonctionnalités dans un ensemble de données et à augmenter l'efficacité des modèles d'apprentissage automatique, il est important de considérer l'impact potentiel sur les performances du modèle et l'interprétabilité des résultats.
Le code complet de cet article :
https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

