Conception et analyse d'algorithmes Java : explication détaillée des exemples d'algorithmes diviser pour régner

1. Introduction

Avant d'apprendre l'algorithme diviser pour régner, laissez-moi vous poser une question. Je crois que tout le monde a l'expérience des tirelires lorsqu'il était jeune. Si les parents et les proches donnent de l'argent, ils y mettront de l'argent. dans leurs propres trésors. Nous chacun Il y aura un moment où l'argent sera compté. Mais vous trouverez peut-être compliqué de gérer une pile d'argent, car les données sont un peu énormes par rapport à votre cerveau et il est facile de faire des erreurs. Vous pouvez les diviser en plusieurs petites parties, puis les additionner pour calculer le total. . Le montant total de cette pile d'argent

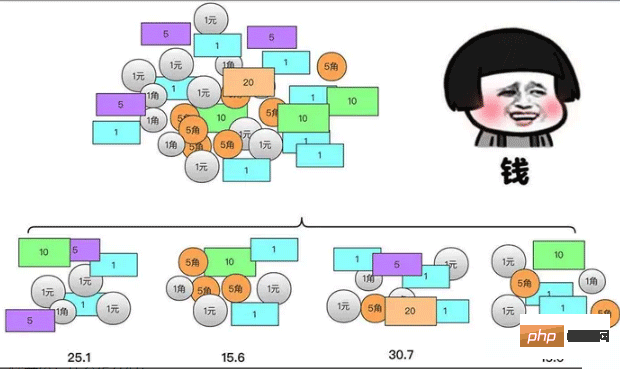
Bien sûr, si vous pensez que la somme d'argent dans chaque partie est encore trop importante, vous pouvez toujours la diviser et la fusionner. La raison pour laquelle nous en avons autant est :

.

• Calculez chaque petit tas d'argent La méthode est la même que la méthode de calcul du plus gros tas d'argent (la différence réside dans la taille)

• Ensuite, la somme du gros tas d'argent est en fait la somme de les résultats du petit tas d’argent. De cette façon, il existe en réalité une mentalité de diviser pour mieux régner.

2. Introduction à l'algorithme diviser pour régner

L'algorithme diviser pour régner est un algorithme qui utilise l'idée de diviser pour régner. Qu'est-ce que diviser pour régner ?

Diviser pour régner, l'explication littérale est « diviser pour régner », qui consiste à diviser un problème complexe en deux ou plusieurs sous-problèmes identiques ou similaires, puis à diviser les sous-problèmes en sous-problèmes plus petits... jusqu'à ce que les sous-problèmes finaux peuvent être résolus simplement et directement, et la solution au problème initial est la combinaison des solutions aux sous-problèmes. En informatique, la méthode diviser pour régner est un algorithme très important qui utilise l’idée diviser pour régner. La méthode diviser pour régner est à la base de nombreux algorithmes efficaces, tels que les algorithmes de tri (tri rapide, tri par fusion), la transformée de Fourier (transformation de Fourier rapide), etc.

Décomposez le problème parent en sous-problèmes et résolvez-les de la même manière. Ceci est cohérent avec le concept de récursion, donc l'algorithme diviser pour régner est généralement implémenté de manière récursive (bien sûr, il existe également des non-problèmes). implémentations récursives).

La description de l'algorithme diviser pour régner est également facile à comprendre littéralement. Diviser pour régner implique en fait un processus de fusion :

• Divider : Résoudre de manière récursive des problèmes plus petits (jusqu'à la couche de terminaison ou arrêter lorsque vous le pouvez). résolvez-le)

• Conquérir : Résolvez de manière récursive Si le problème est suffisamment petit, résolvez-le directement.

• Combiner : Construire la solution du sous-problème en un problème de classe parent

L'algorithme général diviser pour régner est décomposé en deux ou plusieurs appels récursifs dans le texte et en problèmes de sous-classes ne veulent généralement pas être soumis (ne s'influencent pas). Lors de la résolution d'un problème qui est très vaste et difficile à résoudre directement, mais qui est facile à résoudre lorsqu'il est petit et que le problème répond aux conditions applicables de l'algorithme diviser pour régner, alors l'algorithme diviser pour régner peut être utilisé .

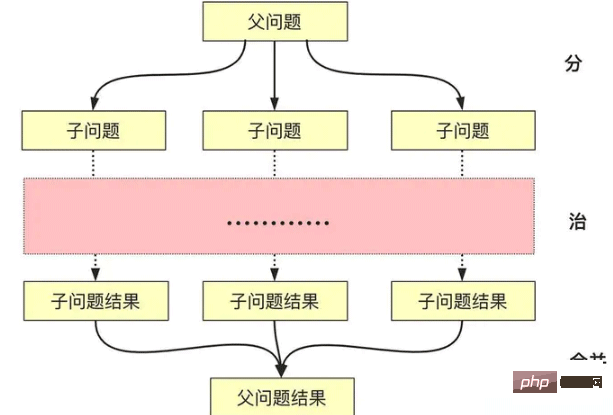
Alors, quelles conditions (caractéristiques) doivent être remplies pour que le problème soit résolu par l'algorithme diviser pour régner

• 1 Le problème d'origine est généralement de grande envergure et difficile à résoudre directement, mais le problème peut être résolu plus facilement s'il est réduit dans une certaine mesure.

• 2. Le problème peut être décomposé en plusieurs sous-problèmes plus petits avec la même méthode de solution (similaire). Et les solutions aux sous-problèmes sont indépendantes et ne s’influencent pas mutuellement.

• 3. La solution au problème peut être obtenue en fusionnant les sous-problèmes de la décomposition du problème.

Vous vous demandez peut-être quelle est la relation entre l'algorithme diviser pour régner et la récursivité ? En fait, diviser pour régner est une pensée importante, axée sur le processus de division, de conquête et de fusion des problèmes. La récursivité est une méthode (outil) qui utilise des méthodes pour s'appeler afin de former un processus de va-et-vient, et diviser pour régner peut tirer parti de plusieurs de ces processus de va-et-vient.

3. Problèmes classiques de l'algorithme Divide and Conquer

Pour les problèmes classiques de l'algorithme Divide and Conquer, l'important est son idée. Parce que nous utilisons principalement la récursion pour l'implémenter, la plupart de l'implémentation du code est très simple, et cet article également L'accent est mis sur le fait de raconter ses pensées.

Le problème classique de l'algorithme diviser pour régner est divisé en deux catégories : les sous-problèmes sont complètement indépendants et les sous-problèmes ne sont pas complètement indépendants.

• 1. Les sous-problèmes sont complètement indépendants, ce qui signifie que la réponse à la question initiale peut être entièrement dérivée des résultats des sous-problèmes.

• 2. Les sous-problèmes ne sont pas complètement indépendants. Certains problèmes d'intervalles ou problèmes inter-intervalles peuvent utiliser diviser pour régner pour aboutir à des intervalles croisés. Vous devez en tirer des leçons approfondies lorsque vous examinez le problème.

3.1. Recherche binaire

La recherche binaire est un exemple de diviser pour régner, mais la recherche binaire a sa propre particularité

• La séquence est ordonnée

• Le résultat est une valeur

Binaire normal recherchera Un intervalle complet est divisé en deux intervalles. Les deux intervalles doivent trouver les valeurs séparément puis confirmer les résultats. Cependant, grâce aux intervalles ordonnés, vous pouvez directement déterminer dans quel intervalle se trouve le résultat, donc les deux intervalles divisés. il suffit de calculer un des intervalles, puis de continuer jusqu'à la fin. Il existe des implémentations récursives et non récursives, mais non récursive est plus couramment utilisé :

public int searchInsert(int[] nums, int target) {
  if(nums[0]>=target)return 0;//剪枝
  if(nums[nums.length-1]==target)return nums.length-1;//剪枝
  if(nums[nums.length-1]<target)return nums.length;
  int left=0,right=nums.length-1;
  while (left<right) {
    int mid=(left+right)/2;
    if(nums[mid]==target)
      return mid;
    else if (nums[mid]>target) {
      right=mid;
    }
    else {
      left=mid+1;
    }
  }
  return left;
}

3.2. Tri rapide

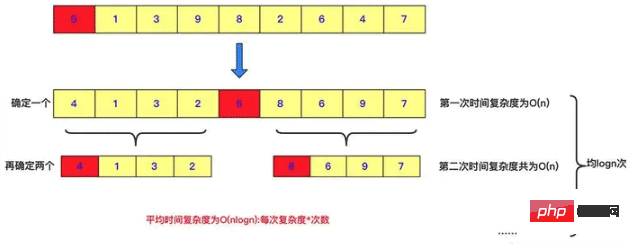
Le tri rapide est également un exemple de diviser pour mieux régner. Chaque passe de tri rapide sélectionnera un nombre, placera le nombre plus petit que ce nombre à gauche et le nombre plus grand que ce nombre à droite. , puis diviser et conquérir récursivement pour résoudre le problème. Pour deux sous-gammes, bien sûr, le tri rapide a fait beaucoup de travail lors de la division. Lorsque tous sont triés au niveau inférieur, la valeur de cette séquence est la valeur triée. C’est une manifestation de diviser pour mieux régner.

public void quicksort(int [] a,int left,int right)
{
  int low=left;
  int high=right;
  //下面两句的顺序一定不能混，否则会产生数组越界！！！very important！！！
  if(low>high)//作为判断是否截止条件
    return;
  int k=a[low];//额外空间k，取最左侧的一个作为衡量，最后要求左侧都比它小，右侧都比它大。
  while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
  {
    while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
    {
      high--;
    }
    //这样就找到第一个比它小的了
    a[low]=a[high];//放到low位置
    while(low<high&&a[low]<=k)//在low往右找到第一个大于k的，放到右侧a[high]位置
    {
      low++;
    }
    a[high]=a[low];
  }
  a[low]=k;//赋值然后左右递归分治求之
  quicksort(a, left, low-1);
  quicksort(a, low+1, right);
}

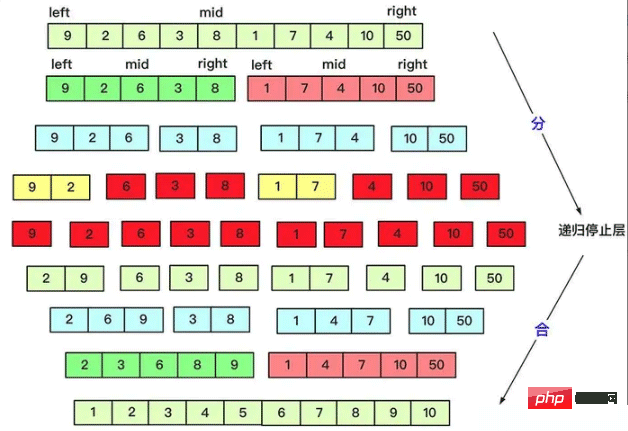
3.3. Tri par fusion (ordre inverse)

Le tri rapide fait beaucoup de travail lors de la division, et la fusion est l'inverse. Lors de la fusion, il divise uniformément en fonction de la quantité, tandis que lors de la fusion, c'est déjà le cas. Fusionnez deux par deux dans l'ordre, car les résultats requis peuvent être obtenus avec une complexité de niveau O (n) de deux séquences ordonnées. La déformation des nombres ordinaux inversés basée sur le tri par fusion est également résolue par l'idée de diviser pour mieux régner.

private static void mergesort(int[] array, int left, int right) {
  int mid=(left+right)/2;
  if(left<right)
  {
    mergesort(array, left, mid);
    mergesort(array, mid+1, right);
    merge(array, left,mid, right);
  }
}
private static void merge(int[] array, int l, int mid, int r) {
  int lindex=l;int rindex=mid+1;
  int team[]=new int[r-l+1];
  int teamindex=0;
  while (lindex<=mid&&rindex<=r) {//先左右比较合并
    if(array[lindex]<=array[rindex])
    {
      team[teamindex++]=array[lindex++];
    }
    else {
      team[teamindex++]=array[rindex++];
    }
  }
  while(lindex<=mid)//当一个越界后剩余按序列添加即可
  {
    team[teamindex++]=array[lindex++];

  }
  while(rindex<=r)
  {
    team[teamindex++]=array[rindex++];
  }	
  for(int i=0;i<teamindex;i++)
  {
    array[l+i]=team[i];
  }
}

3.4. Le problème de la somme maximale des sous-séquences

somme maximale des sous-séquences. Nous pouvons utiliser la programmation dynamique pour résoudre le problème, mais nous pouvons également utiliser l'algorithme diviser pour régner pour résoudre le problème, mais la somme maximale des sous-séquences. n'est pas la même chose lors d'une fusion. Fusion simple, car la somme des sous-séquences implique un problème de longueur, donc les résultats corrects ne sont pas nécessairement tous à gauche ou à droite, mais les résultats possibles sont :

• complètement à gauche de. le milieu

• Complètement sur le côté droit du milieu

• Une séquence contenant les deux nœuds à gauche et à droite du milieu

peut être exprimée dans une image comme :

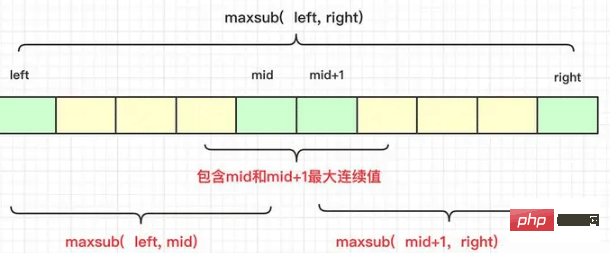
Ainsi, lorsqu'on le considère spécifiquement, il faut exclure la possibilité de récursion. Le résultat de la chaîne de valeur maximale au milieu du résultat obtenu est également calculé pour participer à la comparaison entre les côtés gauche et droit.

Le code implémenté pour la somme maximale des sous-séquences est :

public int maxSubArray(int[] nums) {
    int max=maxsub(nums,0,nums.length-1);
    return max;
}
int maxsub(int nums[],int left,int right)
{
    if(left==right)
        return  nums[left];
    int mid=(left+right)/2;
    int leftmax=maxsub(nums,left,mid);//左侧最大
    int rightmax=maxsub(nums,mid+1,right);//右侧最大
    int midleft=nums[mid];//中间往左
    int midright=nums[mid+1];//中间往右
    int team=0;
    for(int i=mid;i>=left;i--)
    {
        team+=nums[i];
        if(team>midleft)
            midleft=team;
    }
    team=0;
    for(int i=mid+1;i<=right;i++)
    {
        team+=nums[i];
        if(team>midright)
            midright=team;
    }
    int max=midleft+midright;//中间的最大值
    if(max<leftmax)
        max=leftmax;
    if(max<rightmax)
        max=rightmax;
    return  max;
}

3.5.Paire de points la plus proche

La paire de points la plus proche est l'une des applications les plus réussies de diviser pour régner. Il existe plusieurs coordonnées de points sur l'axe de coordonnées bidimensionnel, vous permettant de trouver la distance entre les deux points les plus proches. Si on vous demande de la trouver directement, la violence du dénombrement est une très, très grande quantité de calcul. méthode diviser pour mieux régner pour optimiser ce genre de problème.

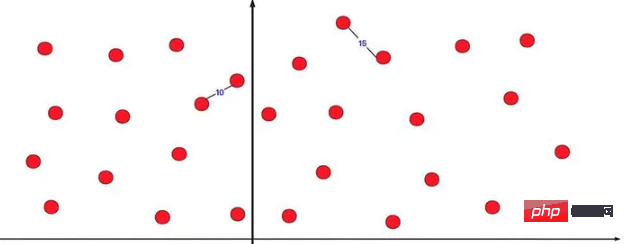
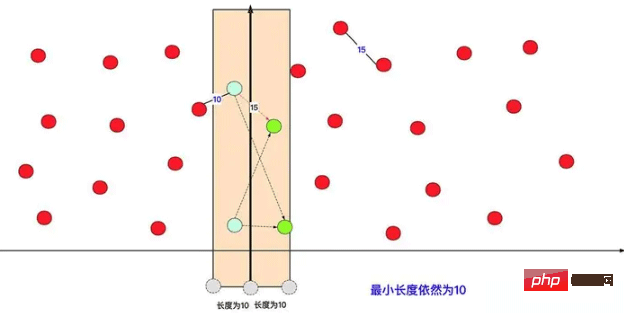
Si vous le divisez directement en deux parties et faites le calcul diviser pour mieux régner, vous constaterez certainement que si la plus courte est une à gauche et une à droite, il y aura un problème. Nous pouvons l'optimiser.

Dans le plan d'optimisation spécifique, considérez la dimension x ou y, divisez les données en deux zones et calculez d'abord (selon la même méthode) les paires de points les plus courtes dans les zones gauche et droite respectivement. Parcourez-le ensuite à gauche et à droite en fonction de la distance la plus courte entre les deux, calculez la distance entre les points couverts gauche et droit, trouvez la plus petite distance et comparez-la avec la distance la plus courte actuelle.

De cette façon, vous pouvez constater qu'avec cette opération ponctuelle (quels que soient les sous-cas), le point rouge de gauche évite le calcul de distance avec la plupart des points rouges de droite (complexité temporelle de O (n2)). En fait, lors de l'exécution de calculs internes dans les intervalles gauche et droit, il effectue en fait de nombreux calculs diviser pour régner de manière récursive. Comme le montre l'image :

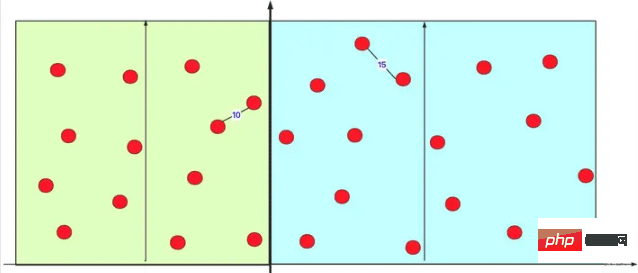
De cette façon, vous pouvez économiser beaucoup de calculs.

Cependant, il y a un problème avec ce type de diviser pour régner, c'est que si les points de coordonnées bidimensionnelles sont tous rassemblés sur une certaine méthode et un certain axe, l'effet peut ne pas être évident (les points sont tous proches x=2 et ont peu d'effet sur la division x). Il faut faire attention. Le code pour

ac est :

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
public class Main {
    static int n;
    public static void main(String[] args) throws IOException {
        StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        //List<node>list=new ArrayList();
         while(in.nextToken()!=StreamTokenizer.TT_EOF)
         {
             n=(int)in.nval;if(n==0) {break;}
            node no[]=new node[n];

             for(int i=0;i<n;i++)
             {
                 in.nextToken();double x=in.nval;
                 in.nextToken();double y=in.nval;
                // list.add(new node(x,y));
                 no[i]=new node(x,y);
             }
             Arrays.sort(no, com);
            double min= search(no,0,n-1);
            out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush();
         }
    }
    private static double search(node[] no, int left,int right) {
        int mid=(right+left)/2;
        double minleng=0;
        if(left==right) {return Double.MAX_VALUE;}
        else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);}
        else minleng= min(search(no,left,mid),search(no,mid,right));
        int ll=mid;int rr=mid+1;
        while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;}
        while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;}
        for(int i=ll;i<rr;i++)
        {
            for(int j=i+1;j<rr+1;j++)
            {
                double team=0;
                if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;}
                else
                {
                    team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y);
                    if(team<minleng)minleng=team;
                }
            }
        }
        return minleng;

    }
    private static double min(double a, double b) {
        // TODO 自动生成的方法存根
        return a<b?a:b;
    }
    static Comparator<node>com=new Comparator<node>() {

        @Override
        public int compare(node a1, node a2) {
            // TODO 自动生成的方法存根
            return a1.y-a2.y>0?1:-1;
        }};
    static class node
    {
        double x;
        double y;
        public node(double x,double y)
        {
            this.x=x;
            this.y=y;
        }
    }
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!