Introduction à l'utilisation et aux algorithmes des énumérations Java

Si vous souhaitez utiliser l'algorithme d'énumération, vous devez d'abord déterminer l'objet d'énumération, la plage d'énumération et les conditions de jugement. Énumérez les solutions possibles une par une, vérifiez si chaque solution est la solution au problème et ne manquez jamais aucune solution correcte possible.

Donnez-moi un exemple

Achetez 100 poulets avec 100 dollars Problème : Il y a une personne qui a 100 dollars et envisage d'acheter 100 poulets. Quand je suis allé au marché, un gros poulet coûtait trois yuans, un petit poulet coûtait trois yuans et un poulet de taille moyenne coûtait deux yuans. Maintenant, s'il vous plaît, écrivez un programme pour l'aider à planifier comment acheter 100 poulets pour exactement 100 yuans ?

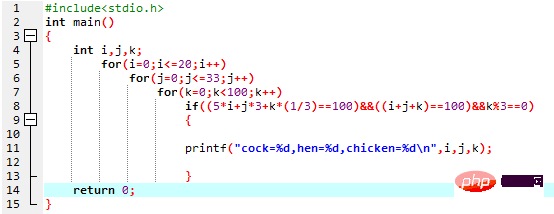
Nous pouvons supposer que le coq est x, la poule est y et le poussin est z, et nous pouvons obtenir l'équation suivante :
 La valeur d'un coq, d'une poule et d'un poussin peut être représentée par le x du coq .

Code :

Le code dans l'image utilise trois boucles for. La complexité temporelle (si vous ne la connaissez pas, ne vous inquiétez pas, il y aura un article spécial pour en discuter plus tard) est O(N). ^3); Nous aimons tous qu'un programme soit simple, qu'il consomme de l'espace, qu'il soit court et concis et qu'il ait l'air haut de gamme. L'optimisation est présentée ci-dessous.

Routines d'optimisation

Bien que l'énumération soit un algorithme très rentable, vous pouvez toujours améliorer l'efficacité de la résolution de problèmes

en rétrécissant la plage d'énumération. Dans le même temps, nous devrions également éviter les énumérations répétées. Regardons la deuxième méthode :

x+y+z = 100 ①

5x+3y+z/3 = 100 ②

Soit ②x3-① obtenir

7x+4y = 100

= > ;y = 25-(7/4)x ③

Et parce que 0

=> 25-7k ⑤

En remplaçant ④⑤ dans ①, nous pouvons savoir

=> z = 75+3k ⑥

Pour garantir que 0

Code :

Ce code a atteint la base d'une boucle à un niveau, et la complexité temporelle est O(n)

Cette châtaigne introduit une routine d'optimisation d'énumération qui est pour réduire le nombre de variables d’énumération à citer. L'ensemble de la routine d'optimisation du dénombrement a principalement deux aspects : l'un consiste à réduire les variables de dénombrement et l'autre est de réduire la portée du dénombrement.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!