Comment implémenter une permutation complète dans l'algorithme Java

Algorithme 1

implémenté basé sur la récursivité et le retour en arrière. Lorsque vous disposez 1, 2 et 3, revenez d'abord de 3 à 2 et constatez qu'il n'y a pas d'autres situations possibles, puis revenez à 1, arrangez 1, 3, 2, puis remontez jusqu'à quand il y a d'autres situations. , c'est-à-dire le nœud racine, puis lorsque vous disposez 2 comme première position, répétez le processus ci-dessus pour mettre tous les résultats possibles dans res.

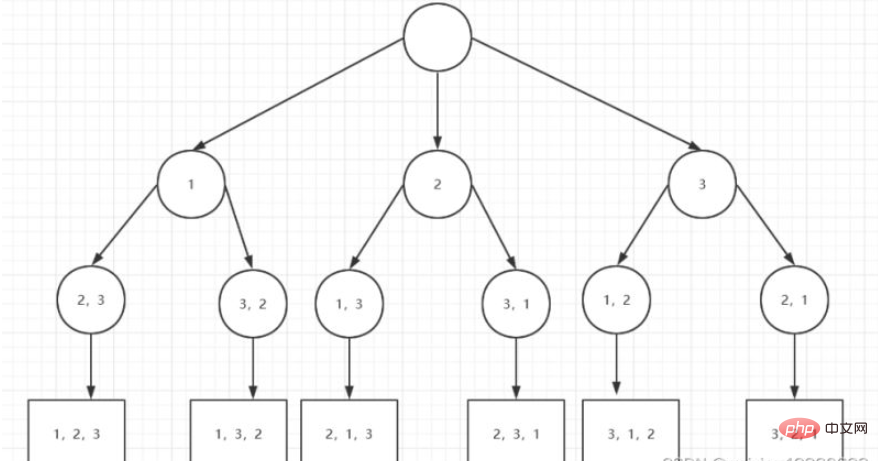
Code :

import java.util.ArrayList;
import java.util.List;
 
public class h718_1 {
 
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
        int[] arr = {1,2,3};
 
        h718_1 h2 = new h718_1();
        h2.dfs(arr,new ArrayList<>());
        for (List<Integer> re : res) {
            System.out.println(re);
        }
 
    }
 
    public List<List<Integer>> dfs( int[] arr,List<Integer> list){
        List<Integer> temp = new ArrayList<>(list);
        if (arr.length == list.size()){
            res.add(temp);
        }
        for (int i=0;i<arr.length;i++){
            if (temp.contains(arr[i])){
                continue;
            }
            temp.add(arr[i]);
            dfs(arr,temp);
            temp.remove(temp.size()-1);
        }
        return res;
    }
 
}

Algorithme 2

Réalisez une permutation complète en échangeant des positions : Supposons que l'ensemble soit {1, 2, 3, 4}

Cycle d'échange de positions : 1 et 1 sont échangés ; sont échangés ; 1 et 3 sont échangés ; 1 et 4 sont échangés

Chaque échange appelle un ensemble plus petit de manière récursive :

Par exemple : le premier échange de 1 et 1 détermine que 1 est en premier lieu, il peut donc être considéré comme {1} + échange récursif {2,3,4} ;

Le premier échange de 1 et 2 détermine que 2 est en premier lieu, il peut donc être considéré comme {2} + échange récursif {1,3 ,4};

La première fois 1 L'échange avec 3 détermine que 3 est en premier lieu, il peut donc être considéré comme {3} + échange récursif {1,2,4};

Le premier échange de 1 et 4 détermine que 4 est en premier lieu, il peut donc être considéré comme {4 } + échange récursif {1,2,3} ;

et ainsi de suite.

Code :

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
public class h718_2 {
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
 
        int[] arr = {1,2,3};
        h718_2 h3 = new h718_2();
        h3.pailie_swap(0,arr);
 
    }
    public void pailie_swap(int index, int[] arr){
        if (arr.length==index){
            System.out.println(Arrays.toString(arr));
            return;
        }
        for (int i = index;i<arr.length;i++){
            swap(i,index,arr);
            pailie_swap(index+1,arr);
            swap(i,index,arr);
        }
 
    }
 
    public void swap(int i,int j ,int[] arr){
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
 
    }
}

Algorithme 3

Vous pouvez obtenir un arrangement complet en ajoutant des éléments :

Définissez d'abord une liste et placez-y le premier élément, puis insérez les éléments restants dans l'ordre dans toutes les positions possibles des éléments de l'ensemble précédent ; Générez une nouvelle liste ;

Par exemple : pour obtenir un arrangement complet de {1,2,3,4}

Définissez d'abord une liste et ajoutez le premier élément comme {1}, puis le deuxième élément 2 peut être inséré dans { ; 1} Les deux positions avant et après forment une nouvelle liste : {21, 12}, et le troisième élément 3 est inséré dans toutes les positions des éléments de la liste : {321, 231, 213, 312, 132, 123} ; et ainsi de suite.

Code :

import java.util.ArrayList;
 
public class h718_3 {
 
    public static void main(String[] args) {
        String aa = "123";
        h718_3 h4 = new h718_3();
        ArrayList<String> res = new ArrayList<>();
        res = h4.getPermutation0(aa);
 
        for (String re : res) {
            System.out.println(re);
        }
 
    }
 
    public ArrayList<String> getPermutation0(String A) {
        int n = A.length();
        ArrayList<String> res = new ArrayList<>();
        res.add(A.charAt(0) + "");//初始化,包含第一个字符
 
        for (int i = 1; i < n; i++) {//第二个字符插入到前面生成集合的每个元素里面
            ArrayList<String> res_new = new ArrayList<>();
            char c = A.charAt(i);//新字符
            for (String str : res) {//访问上一趟集合中的每个字符串
                //  插入到每个位置,形成一个新串
                String newStr = c + str;//加在前面
                res_new.add(newStr);
                newStr = str + c;//加在后面
                res_new.add(newStr);
                //加在中间
                for (int j = 1; j < str.length(); j++) {
                    newStr = str.substring(0, j) + c + str.substring(j);
                    res_new.add(newStr);
                }
            }
            res = res_new;//更新
 
        }
        return res;
    }
}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!