Comment implémenter un algorithme génétique en utilisant Python

遗传算法 est une méthode de recherche et d’optimisation globale stochastique développée en imitant le mécanisme d’évolution biologique dans la nature. Elle s’appuie sur la théorie de l’évolution de Darwin et la théorie de la génétique de Mendel. Son essence est une méthode de recherche efficace, parallèle et globale qui peut automatiquement acquérir et accumuler des connaissances sur l'espace de recherche pendant le processus de recherche, et contrôler de manière adaptative le processus de recherche pour obtenir la solution optimale. Les opérations des algorithmes génétiques utilisent le principe de survie du plus apte pour générer successivement une solution quasi optimale dans la population de solutions potentielles à chaque génération de l'algorithme génétique, en fonction de la valeur de fitness de l'individu dans le domaine problématique et de la génétique naturelle. une méthode de reconstruction empruntée à la littérature chinoise est utilisée pour la sélection individuelle afin de générer une nouvelle solution approchée. Ce processus conduit à l'évolution des individus dans la population, et les nouveaux individus qui en résultent sont mieux adaptés à l'environnement que les individus d'origine, tout comme la transformation de la nature.

Étapes spécifiques de l'algorithme génétique :

(1) Initialisation : définissez le compteur de génération évolutive t = 0, définissez la génération évolutive maximale T, la probabilité de croisement, la probabilité de mutation et générez aléatoirement M individus comme population initiale P

(2) Évaluation individuelle : Calculer l'aptitude de chaque individu dans la population P

(3) Opération de sélection : Appliquer l'opérateur de sélection à la population. En fonction de la condition physique individuelle, sélectionnez l'individu optimal pour en hériter directement à la génération suivante ou générer de nouveaux individus par croisement par paire, puis en hériter à la génération suivante

(4) Opération de croisement : sous le contrôle de la probabilité de croisement, deux individus dans le groupe croise les deux

(5) Opération de mutation : Sous le contrôle de la probabilité de mutation, les individus de la population sont mutés, c'est-à-dire que les gènes d'un certain individu sont ajustés au hasard

(6) Après sélection, croisement , et les opérations de mutation, nous obtenons le groupe P1 de nouvelle génération.

Répétez les étapes (1) à (6) ci-dessus jusqu'à ce que la génération génétique soit T, utilisez l'individu avec la forme physique optimale obtenue au cours du processus d'évolution comme résultat de solution optimale et terminez le calcul.

Problème du voyageur de commerce (TSP) : il y a n villes. Un vendeur doit partir d'une des villes, visiter toutes les villes, puis revenir à la ville où il a commencé pour trouver l'itinéraire le plus court.

Certaines conventions sont nécessaires lors de l'application de l'algorithme génétique pour résoudre le problème TSP. Un gène est un ensemble de séquences de villes, et la fitness est la somme des distances des séquences de villes selon ce gène.

1.2 Code expérimental

import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典，防止下面被当成列表
cities={}
for line in data:
    #原始数据以\n换行，将其替换掉
    line=line.replace("\n","")
    #最后一行以EOF为标志，如果读到就证明读完了，退出循环
    if(line=="EOF"):
        break
    #空格分割城市编号和城市的坐标
    city=line.split(" ")
    map(int,city)
    #将城市数据添加到cities中
    cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
 
# 计算适应度，也就是距离分之一，这里用伪欧氏距离
def calcfit(gene):
    sum=0
    #最后要回到初始城市所以从-1，也就是最后一个城市绕一圈到最后一个城市
    for i in range(-1,len(gene)-1):
        nowcity=gene[i]
        nextcity=gene[i+1]
        nowloc=cities[nowcity]
        nextloc=cities[nextcity]
        sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
 
    return 1/sum
 
# 每个个体的类，方便根据基因计算适应度
class Person:
    def __init__(self,gene):
        self.gene=gene
        self.fit=calcfit(gene)
class Group:
    def __init__(self):
        self.GroupSize=100  #种群规模
        self.GeneSize=48    #基因数量，也就是城市数量
        self.initGroup()
        self.upDate()
    #初始化种群，随机生成若干个体
    def initGroup(self):
        self.group=[]
        i=0
        while(i<self.GroupSize):
            i+=1
            #gene如果在for以外生成只会shuffle一次
            gene=[i+1 for i in range(self.GeneSize)]
            random.shuffle(gene)
            tmpPerson=Person(gene)
            self.group.append(tmpPerson)
 
    #获取种群中适应度最高的个体
    def getBest(self):
        bestFit=self.group[0].fit
        best=self.group[0]
        for person in self.group:
            if(person.fit>bestFit):
                bestFit=person.fit
                best=person
        return best
    #计算种群中所有个体的平均距离
    def getAvg(self):
        sum=0
        for p in self.group:
            sum+=1/p.fit
        return sum/len(self.group)
    #根据适应度，使用轮盘赌返回一个个体，用于遗传交叉
    def getOne(self):
        #section的简称，区间
        sec=[0]
        sumsec=0
        for person in self.group:
            sumsec+=person.fit
            sec.append(sumsec)
        p=random.random()*sumsec
        for i in range(len(sec)):
            if(p>sec[i] and p<sec[i+1]):
                #这里注意区间是比个体多一个0的
                return self.group[i]
    #更新种群相关信息
    def upDate(self):
        self.best=self.getBest()
# 遗传算法的类，定义了遗传、交叉、变异等操作
class GA:
    def __init__(self):
        self.group=Group()
        self.pCross=0.35    #交叉率
        self.pChange=0.1    #变异率
        self.Gen=1  #代数
 
    #变异操作
    def change(self,gene):
        #把列表随机的一段取出然后再随机插入某个位置
        #length是取出基因的长度，postake是取出的位置，posins是插入的位置
        geneLenght=len(gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(0, geneLenght - 1)
        newGene = gene[:]       # 产生一个新的基因序列，以免变异的时候影响父种群
        newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
        return newGene
 
    #交叉操作
    def cross(self,p1,p2):
        geneLenght=len(p1.gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(index1, geneLenght - 1)
        tempGene = p2.gene[index1:index2]   # 交叉的基因片段
        newGene = []
        p1len = 0
        for g in p1.gene:
              if p1len == index1:
                    newGene.extend(tempGene)     # 插入基因片段
                    p1len += 1
              if g not in tempGene:
                    newGene.append(g)
                    p1len += 1
        return newGene
 
    #获取下一代
    def nextGen(self):
        self.Gen+=1
        #nextGen代表下一代的所有基因
        nextGen=[]
        #将最优秀的基因直接传递给下一代
        nextGen.append(self.group.getBest().gene[:])
        while(len(nextGen)<self.group.GroupSize):
            pChange=random.random()
            pCross=random.random()
            p1=self.group.getOne()
            if(pCross<self.pCross):
                p2=self.group.getOne()
                newGene=self.cross(p1,p2)
            else:
                newGene=p1.gene[:]
            if(pChange<self.pChange):
                newGene=self.change(newGene)
            nextGen.append(newGene)
        self.group.group=[]
        for gene in nextGen:
            self.group.group.append(Person(gene))
            self.group.upDate()
 
    #打印当前种群的最优个体信息
    def showBest(self):
        print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
 
    #n代表代数，遗传算法的入口
    def run(self,n):
        Gen=[]  #代数
        dist=[] #每一代的最优距离
        avgDist=[]  #每一代的平均距离
        #上面三个列表是为了画图
        i=1
        while(i<n):
            self.nextGen()
            self.showBest()
            i+=1
            Gen.append(i)
            dist.append(1/self.group.getBest().fit)
            avgDist.append(self.group.getAvg())
        #绘制进化曲线
        plt.plot(Gen,dist,&#39;-r&#39;)
        plt.plot(Gen,avgDist,&#39;-b&#39;)
        plt.show()
 
ga=GA()
ga.run(3000)
print("进行3000代后最优解：",1/ga.group.getBest().fit)

1.3 Résultats expérimentaux

L'image ci-dessous est une capture d'écran des résultats d'une expérience. La solution optimale est 11271

Afin d'éviter le hasard de l'expérience, l'expérience a été répétée. 10 fois et le résultat a été obtenu Moyen, les résultats sont les suivants.

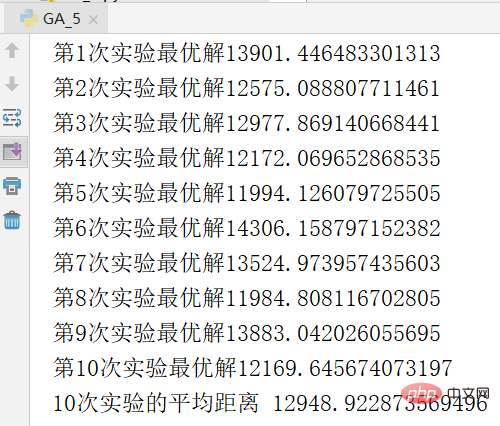
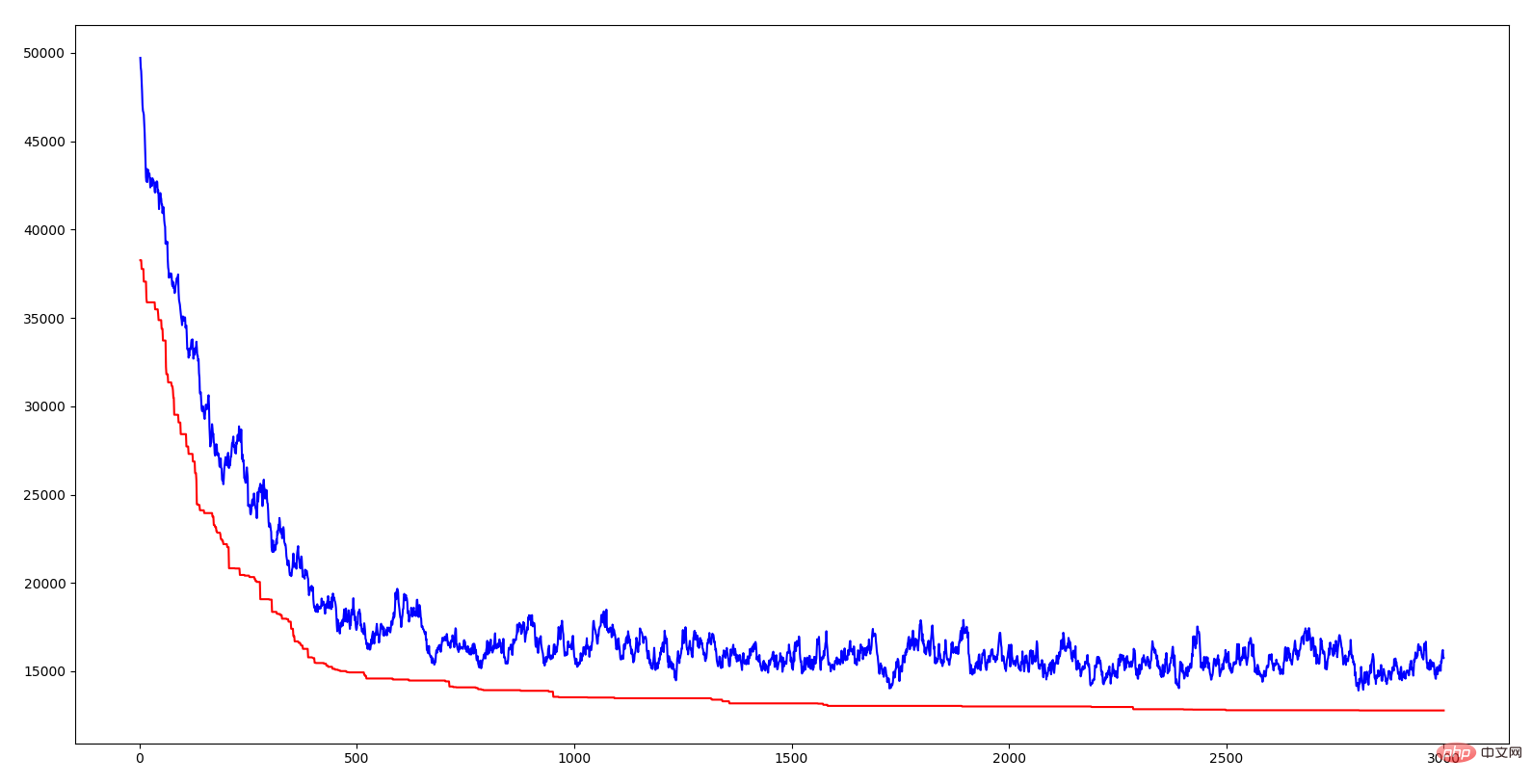
L'abscisse dans la figure ci-dessus est l'algèbre, l'ordonnée est la distance, la courbe rouge est la distance de l'individu optimal de chaque génération et la courbe bleue est la distance moyenne de chaque génération. On peut voir que les deux lignes ont une tendance à la baisse, ce qui signifie qu’elles évoluent. La diminution de la distance moyenne indique qu'en raison de l'émergence d'excellents gènes (c'est-à-dire d'une certaine séquence urbaine), cet excellent trait se propage rapidement à l'ensemble de la population. Tout comme la survie des plus forts dans la nature, seuls ceux qui possèdent des gènes qui s'adaptent à l'environnement peuvent survivre. Par conséquent, ceux qui survivent sont ceux qui possèdent d'excellents gènes. L'importance de l'introduction du taux de croisement et du taux de mutation dans l'algorithme est de garantir l'excellente qualité des gènes actuels et d'essayer de générer de meilleurs gènes. Si tous les individus se croisent, certains segments génétiques excellents peuvent être perdus ; si aucun ne se croise, alors deux segments génétiques excellents ne peuvent pas être combinés en de meilleurs gènes ; s’il n’y a pas de variation, des individus plus adaptés à l’environnement ne peuvent pas être produits. Je dois soupirer parce que la sagesse de la nature est si puissante.

Le fragment de gène mentionné ci-dessus est une courte séquence de ville dans TSP Lorsque la somme des distances d'une certaine séquence est relativement petite, cela signifie que cette séquence est un ordre de traversée relativement bon pour ces villes. L'algorithme génétique réalise une optimisation continue de la solution TSP en combinant ces excellents fragments. La méthode combinée s’appuie sur la sagesse de la nature, l’héritage, la mutation et la survie du plus fort.

1.4 Résumé de l'expérience

1. Comment parvenir à la « survie du plus fort » dans l'algorithme ?

La soi-disant survie du plus fort signifie la rétention d'excellents gènes et l'élimination de gènes qui ne sont pas adaptés à l'environnement. Dans l'algorithme GA ci-dessus, j'utilise la roulette, c'est-à-dire que dans l'étape génétique (qu'elle soit croisée ou non), chaque individu est sélectionné en fonction de sa forme physique. De cette manière, les individus ayant une bonne forme physique peuvent avoir plus de progéniture, atteignant ainsi l’objectif de survie du plus fort.

Lors du processus spécifique de mise en œuvre, j'ai commis une erreur lors de la sélection des individus à l'étape génétique, j'ai supprimé cet individu du groupe à chaque fois que je le sélectionnais. En y réfléchissant maintenant, cette approche était très stupide. Même si j'avais déjà mis en œuvre la roulette à l'époque, si l'individu était sélectionné et supprimé, chaque individu donnerait naissance à une progéniture égale. La soi-disant roulette n'est qu'un moyen. laisser ceux qui ont une bonne forme physique être hérités en premier. Cette approche s'écarte complètement de l'intention initiale de « la survie du plus fort ». L'approche correcte consiste à sélectionner les individus à hériter, puis à les réintégrer dans la population. Cela peut garantir que les individus ayant une bonne condition physique seront hérités plusieurs fois, produiront plus de progéniture et diffuseront plus largement d'excellents gènes. produira peu de progéniture ou sera éliminé directement.

2. Comment s'assurer que l'évolution progresse toujours dans un sens positif ?

La soi-disant progression vers l'avant signifie que les individus optimaux de la prochaine génération doivent être plus ou tout aussi adaptables à l'environnement que la génération précédente. La méthode que j’adopte est que l’individu optimal entre directement dans la génération suivante sans participer à des opérations telles qu’une mutation croisée. Cela peut empêcher l’évolution inverse de « contaminer » les meilleurs gènes actuellement dus à ces opérations.

J'ai également rencontré un autre problème lors du processus d'implémentation, qu'il soit dû au passage par référence ou par valeur. Lors du croisement et de la mutation de gènes individuels, une liste est utilisée. Lors de la transmission de la liste en Python, il s'agit en fait d'une référence. Cela entraînera la modification des propres gènes de l'individu après le croisement et la mutation de l'individu. Le résultat est une évolution très lente, accompagnée d'une évolution inverse.

3. Comment réaliser le crossover ?

Sélectionnez les fragments d'un individu et placez-les dans un autre individu, puis placez les gènes non dupliqués dans d'autres positions dans l'ordre.

Lors de la mise en œuvre de cette étape, j'ai mal implémenté cette fonction en raison de ma compréhension inhérente du comportement des chromosomes réels lors de l'étude de la biologie, "les chromosomes homologues se croisent et échangent des segments homologues". J'ai seulement interverti les fragments des deux individus au même endroit pour compléter le croisement. Évidemment, cette approche est erronée et conduira à la duplication des villes.

4. Lorsque j'ai commencé à écrire cet algorithme, je l'ai écrit à moitié POO et à moitié orienté processus.

Lors des tests ultérieurs, j'ai trouvé qu'il était difficile de modifier les paramètres et de mettre à jour les informations individuelles, j'ai donc tout changé en POO, ce qui l'a rendu beaucoup plus pratique. La POO offre une grande flexibilité et simplicité pour simuler des problèmes du monde réel comme celui-ci.

5. Comment prévenir l’apparition de solutions optimales locales ?

Au cours du processus de test, il a été constaté que des solutions optimales locales apparaissent occasionnellement, qui ne continueront pas à évoluer avant longtemps, et les solutions actuelles sont loin de la solution optimale. Même après des ajustements ultérieurs, bien qu'il soit proche de la solution optimale, il s'agit toujours d'un « optimal local » car il n'a pas encore atteint la solution optimale.

L'algorithme convergera très rapidement au début, mais deviendra de plus en plus lent au fur et à mesure, voire ne bougera pas du tout. Parce qu'à un stade ultérieur, tous les individus ont d'excellents gènes relativement similaires, l'effet du croisement sur l'évolution à ce moment est très faible, et la principale force motrice de l'évolution devient la mutation, et la mutation est un algorithme violent. Si vous avez de la chance, vous pourrez rapidement muter pour devenir un meilleur individu, mais si vous n'avez pas de chance, vous devrez attendre.

La solution pour empêcher les solutions optimales locales est d'augmenter la taille de la population, afin qu'il y ait plus de mutations individuelles et qu'il y ait une plus grande possibilité de produire des individus évolués. L’inconvénient de l’augmentation de la taille de la population est que le temps de calcul de chaque génération va s’allonger, ce qui signifie que les deux s’inhibent mutuellement. Bien qu'une population très grande puisse finalement éviter des solutions optimales locales, chaque génération prend beaucoup de temps, et il faut beaucoup de temps pour trouver la solution optimale, alors qu'une population plus petite, bien que le temps de calcul de chaque génération soit rapide, ne le sera pas ; résolu après plusieurs générations tombera dans un optimum local.

Conjecture, une méthode d'optimisation possible consiste à utiliser une taille de population plus petite dans les premiers stades de l'évolution pour accélérer l'évolution lorsque la condition physique atteint un certain seuil, augmenter la taille de la population et le taux de mutation pour éviter l'émergence de solutions optimales locales. . Cette méthode d'ajustement dynamique est utilisée pour peser l'équilibre entre l'efficacité informatique de chaque génération et l'efficacité informatique globale.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!