Quelles sont les méthodes de normalisation courantes en Python ?

La normalisation des données est une étape très critique dans le prétraitement des données d'apprentissage en profondeur, qui peut unifier les dimensions et empêcher l'absorption de petites données.

1 : Le concept de normalisation

La normalisation consiste à convertir toutes les données en nombres compris entre [0,1] ou [-1,1]. Son but est d'éliminer les différences entre les données dans chaque dimension. La différence d'amplitude empêche l'erreur de prédiction du réseau d'être trop importante en raison de la grande différence d'ordre de grandeur entre les données d'entrée et de sortie.

2 : Le rôle de la normalisation

1. Pour faciliter le traitement ultérieur des données, la normalisation peut éviter certains problèmes numériques inutiles.

2. Afin de converger plus rapidement lorsque le programme est en cours d'exécution

3. unifiez les dimensions. Les critères d'évaluation des exemples de données sont différents, ils doivent donc être dimensionnés et les critères d'évaluation unifiés. Ceci est considéré comme une exigence au niveau de l'application.

4. Évitez la saturation neuronale. C'est-à-dire que lorsque l'activation des neurones est proche de 0 ou 1, dans ces zones, le gradient est proche de 0, de sorte que lors du processus de rétro-propagation, le gradient local sera proche de 0, ce qui est très défavorable au réseau. entraînement.

5. Assurez-vous que les petites valeurs dans les données de sortie ne seront pas avalées.

Trois : Types de normalisation

1 : Normalisation linéaire

La normalisation linéaire est également appelée normalisation min-max ; est une transformation linéaire des données d'origine, convertissant les valeurs des données Map entre [0 ,1]. Elle s'exprime comme suit :

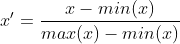
La standardisation des différences conserve la relation existant dans les données d'origine et constitue la méthode la plus simple pour éliminer l'influence des dimensions et des plages de valeurs des données. Le code est implémenté comme suit :

def MaxMinNormalization(x,Max,Min):
    x = (x - Min) / (Max - Min);
    return x

Champ d'application : Plus adapté aux situations où les valeurs numériques sont relativement concentrées

Inconvénients :

1. Si max et min sont instables, il est facile de rendre le résultat normalisé instable , rendant l'utilisation ultérieure moins efficace. Si la plage de valeurs dépasse l'attribut actuel [min, max], le système signalera une erreur. Min et max doivent être redéterminés.

2. Si une certaine valeur dans l'ensemble de valeurs est très grande, alors les valeurs normalisées seront proches de 0 et ne différeront pas beaucoup. (tels que 1,1.2,1.3,1.4,1.5,1.6,10) cet ensemble de données.

2 : Normalisation à moyenne nulle (normalisation du score Z)

La normalisation du score Z est également appelée normalisation de l'écart type. La moyenne des données traitées est de 0 et l'écart type est de 1. La formule de conversion est la suivante :

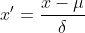
où 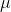est la moyenne des données originales, 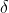est l'écart type des données originales, qui est la formule de standardisation la plus couramment utilisée

Cette méthode donne la moyenne et l'écart type des les données originales (écart type) normalisent les données. Les données traitées sont conformes à la distribution normale standard, c'est-à-dire que la moyenne est de 0 et l'écart type est de 1. La clé ici est la distribution normale standard composite

Le code est implémenté comme suit :

def Z_ScoreNormalization(x,mu,sigma):
    x = (x - mu) / sigma;
    return x

3 : Normalisation de l'échelle décimale

Cette méthode est passée Déplacez les décimales de la valeur de l'attribut et mappez la valeur de l'attribut entre [-1,1]. Le nombre de décimales déplacées dépend de la valeur absolue maximale de la valeur de l'attribut. La formule de conversion est la suivante :

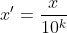
4 : Normalisation non linéaire

Cette méthode inclut log, exponentielle, tangente

Champ d'application : souvent utilisé dans des scénarios d'analyse de données relativement volumineux, certaines valeurs sont très grandes, d'autres sont très petit, mappez la valeur d'origine.

4 : Normalisation par lots

1 : Introduction

Dans la précédente formation sur les réseaux neuronaux, seules les données de la couche d'entrée étaient normalisées, mais il n'y avait pas de normalisation dans la couche intermédiaire. Bien que nous ayons normalisé les données d'entrée, une fois que les données d'entrée ont subi une multiplication matricielle comme celle-ci, leur distribution de données est susceptible de changer considérablement et à mesure que le nombre de couches du réseau continue de s'approfondir. La distribution des données va changer de plus en plus. Par conséquent, ce processus de normalisation dans la couche intermédiaire du réseau neuronal, qui améliore l'effet d'entraînement, est appelé normalisation par lots (BN)

2 : Les avantages de l'algorithme BN

1. réduit la sélection artificielle des paramètres

2. réduit l'exigence de taux d'apprentissage. Nous pouvons utiliser un taux d'apprentissage élevé dans l'état initial ou lors de l'utilisation d'un taux d'apprentissage plus faible, l'algorithme peut également s'entraîner et converger rapidement.

3. Remplace la distribution des données d'origine, ce qui atténue dans une certaine mesure le surajustement (empêchant qu'un certain échantillon soit fréquemment sélectionné dans chaque lot d'entraînement)

4. Réduit la disparition du gradient, accélère la convergence et améliore la précision de l'entraînement.

3 : Processus de l'algorithme de normalisation par lots (BN)

Entrée : résultat de sortie de la couche précédente

1) Calculer la moyenne des données de sortie de la couche précédente :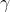

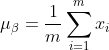
Parmi eux, m est la taille de ce lot d'échantillons de formation.

2) Calculez l'écart type des données de sortie de la couche précédente :

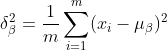
3) Processus de normalisation pour obtenir

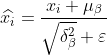
Le dans la formule est d'éviter que le dénominateur soit 0 et d'ajouter une petite valeur valeur proche de 0.

4) Reconstruction, reconstruisez les données obtenues après le processus de normalisation ci-dessus et obtenez :

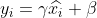
où 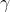, 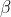sont des paramètres apprenables.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!