Richard Sutton a déclaré sans ambages que la rétropropagation convolutive a pris du retard et que les percées de l'IA nécessitent de nouvelles idées : la rétropropagation continue

La « perte de plasticité » est l'une des lacunes les plus fréquemment critiquées des réseaux de neurones profonds, ce qui est également l'une des raisons pour lesquelles les systèmes d'IA basés sur l'apprentissage profond sont considérés comme incapables de continuer à apprendre.

Pour le cerveau humain, la « plasticité » fait référence à la capacité à générer de nouveaux neurones et de nouvelles connexions entre neurones, ce qui constitue une base importante pour l'apprentissage continu. À mesure que nous vieillissons, la plasticité du cerveau diminue progressivement au détriment de la consolidation de ce que nous avons appris. Les réseaux de neurones sont similaires.

Un exemple frappant est que la formation à démarrage à chaud en 2020 a fait ses preuves : ce n'est qu'en abandonnant ce qui a été initialement appris et en s'entraînant sur l'ensemble des données de manière ponctuelle que l'on peut obtenir des comparaisons. Un bon effet d'apprentissage.

Dans l'apprentissage par renforcement profond (DRL), le système d'IA doit souvent "oublier" tout le contenu précédemment appris par le réseau neuronal, enregistrer seulement une partie du contenu dans le tampon de lecture, puis recommencer de zéro à parvenir à un apprentissage continu. Cette façon de réinitialiser le réseau est également considérée comme la preuve que le deep learning ne peut pas continuer à apprendre.

Alors, comment pouvons-nous garder les systèmes d'apprentissage malléables ?

Récemment, Richard Sutton, le père de l'apprentissage par renforcement, a prononcé un discours intitulé "Maintaining Plasticity in Deep Continual Learning" lors de la conférence CoLLAs 2022, et a proposé une réponse qui, selon lui, pourrait résoudre ce problème : Algorithme de rétropropagation continue ( Backprop continu).

Richard Sutton a d'abord prouvé l'existence d'une perte de plasticité du point de vue de l'ensemble de données, puis a analysé les causes de la perte de plasticité à l'intérieur du réseau neuronal et a finalement proposé l'algorithme de rétropropagation continue comme moyen de résoudre la perte de plasticité. : Réinitialisation d'un petit nombre de neurones de faible utilité, Cette injection continue de diversité peut maintenir indéfiniment la plasticité des réseaux profonds.

Ce qui suit est le texte intégral du discours, qui a été compilé par AI Technology Review sans changer le sens original.

1 L'existence réelle de la perte de plasticité

Le deep learning peut-il vraiment résoudre le problème de l'apprentissage continu ?

La réponse est non, principalement pour les trois points suivants :

1. « Insoluble » signifie que comme un réseau linéaire non profond, la vitesse d'apprentissage sera finalement très lente
2. utilisé en profondeur ; apprentissage Les méthodes de standardisation professionnelles ne sont efficaces que dans l'apprentissage ponctuel et sont contraires à l'apprentissage continu ;
3. La mise en cache de relecture elle-même est une méthode extrême pour admettre que l'apprentissage en profondeur n'est pas réalisable ;

Par conséquent, Nous devons trouver de meilleurs algorithmes adaptés à ce nouveau modèle d'apprentissage et nous débarrasser des limites de l'apprentissage ponctuel.

Tout d'abord, nous utilisons les ensembles de données ImageNet et MNIST pour les tâches de classification afin de réaliser une prédiction de régression, de tester directement l'effet d'apprentissage continu et de prouver l'existence d'une perte de plasticité dans l'apprentissage supervisé.

Test de l'ensemble de données ImageNet

ImageNet est un ensemble de données contenant des millions d'images étiquetées avec des noms. Il comporte 1 000 catégories avec 700 images ou plus par catégorie et est largement utilisé pour l'apprentissage et la prédiction de catégories.

Ci-dessous, une photo d'un requin, sous-échantillonnée à la taille 32*32. Le but de cette expérience est de trouver des changements minimes par rapport aux pratiques d'apprentissage profond. Nous avons divisé les 700 images de chaque catégorie en 600 échantillons d'apprentissage et 100 échantillons de test, puis divisé les 1 000 catégories en deux groupes pour générer une séquence de tâches de classification binaire d'une longueur de 500. Tous les ensembles de données ont été mélangés de manière aléatoire. Après un entraînement pour chaque tâche, nous évaluons la précision du modèle sur l'échantillon de test, l'exécutons 30 fois indépendamment et prenons la moyenne avant d'entrer dans la tâche de classification binaire suivante.

500 tâches de classification partageront le même réseau Afin d'éliminer l'impact de la complexité, le réseau principal sera réinitialisé après le changement de tâche. Nous utilisons un réseau standard, c'est-à-dire 3 couches de convolution + 3 couches entièrement connectées, mais la couche de sortie peut être relativement petite pour l'ensemble de données ImageNet car seules deux catégories sont utilisées dans une tâche. Pour chaque tâche, 100 exemples sont pris sous forme de lot, avec un total de 12 lots et 250 époques de formation. Une seule initialisation est effectuée avant de démarrer la première tâche, en utilisant la distribution de Kaiming pour initialiser les poids. La descente de gradient stochastique basée sur l'impulsion est utilisée pour la perte d'entropie croisée, et la fonction d'activation ReLU est utilisée.

Cela amène à deux questions :

1. Comment la performance va-t-elle évoluer dans la séquence de tâches ?

2. Sur quelle tâche la performance sera-t-elle meilleure ? La première mission initiale est-elle meilleure ? Ou les tâches ultérieures bénéficieront-elles de l’expérience des tâches précédentes ?

La réponse est donnée dans la figure ci-dessous : La performance de l'apprentissage continu est entièrement déterminée par la taille de l'étape de formation et la rétropropagation.

Puisqu'il s'agit d'un problème de classification binaire, la probabilité de chance est de 50 %. La zone ombrée représente l'écart type, et cette différence n'est pas significative. Le benchmark linéaire utilise une couche linéaire pour traiter directement les valeurs des pixels, ce qui n'est pas aussi efficace que la méthode d'apprentissage en profondeur. Cette différence est significative.

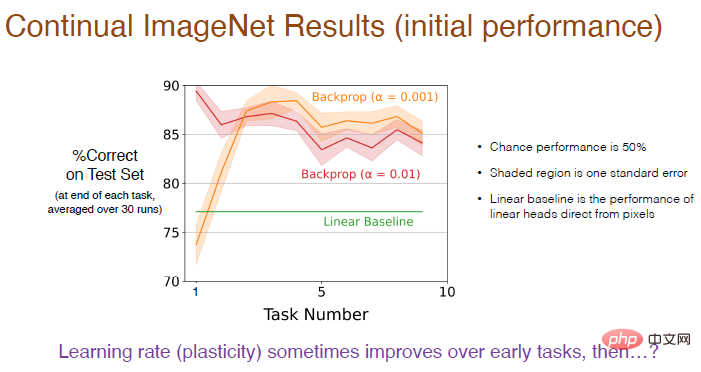
Illustration : L'utilisation d'un taux d'apprentissage plus faible (α=0,001) aura une plus grande précision et les performances s'amélioreront progressivement dans les 5 premières tâches, mais elles montreront une tendance à la baisse à long terme.

Nous avons ensuite augmenté le nombre de tâches à 2000 et analysé plus en détail l'impact du taux d'apprentissage sur l'effet d'apprentissage continu. En moyenne, la précision a été calculée toutes les 50 tâches. Le résultat est présenté ci-dessous.

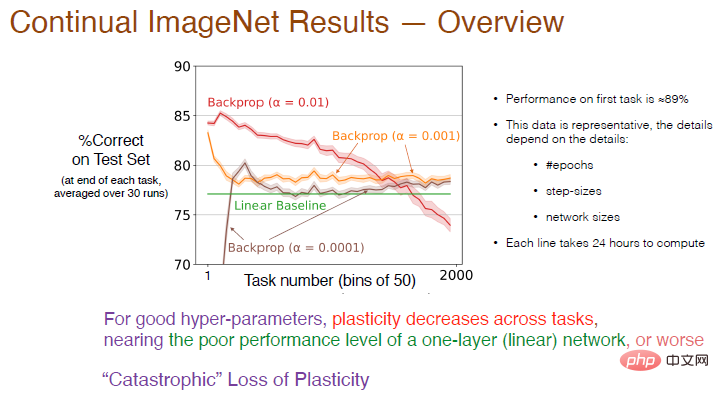
Légende : La précision de la courbe rouge avec α=0,01 sur la première tâche est d'environ 89%. Une fois que le nombre de tâches dépasse 50, la précision diminue à mesure que le nombre de tâches augmente encore, la plasticité. Peu à peu manquante, la précision finale est inférieure à la ligne de base linéaire. Lorsque α = 0,001, la vitesse d'apprentissage ralentit, la plasticité diminue également fortement et la précision n'est que légèrement supérieure à celle du réseau linéaire.

Par conséquent, pour de bons hyperparamètres, la plasticité entre les tâches diminuera et la précision sera inférieure à l'utilisation d'une seule couche de réseaux neuronaux. Ce que montre la courbe rouge est presque une "perte de plasticité catastrophique".

Les résultats de la formation dépendent également de paramètres tels que le nombre d'itérations, le nombre d'étapes et la taille du réseau. Le temps de formation pour chaque courbe de la figure est de 24 heures sur plusieurs processeurs, ce qui peut ne pas être pratique lorsque. faire des expériences systématiques. Nous sélectionnons ensuite l’ensemble de données MNIST pour les tests.

MNIST Dataset Test

L'ensemble de données MNIST contient un total de 60 000 images de chiffres manuscrits, avec 10 catégories de 0 à 9, et sont 28*28 images en niveaux de gris.

Goodfellow et al. ont créé une nouvelle tâche de test en mélangeant l'ordre ou en disposant les pixels de manière aléatoire. L'image dans le coin inférieur droit est un exemple de l'image organisée générée. dans chaque Dans chaque tâche, 6000 images sont présentées de manière aléatoire. Aucun contenu de tâche n'est ajouté ici et les pondérations du réseau ne sont initialisées qu'une seule fois avant la première tâche. Nous pouvons utiliser la perte d'entropie croisée en ligne pour la formation et continuer à utiliser l'indice de précision pour mesurer l'effet de l'apprentissage continu.

La structure du réseau neuronal est composée de 4 couches entièrement connectées, le nombre de neurones dans les 3 premières couches est de 2000 et le nombre de neurones dans la dernière couche est de 10. Étant donné que les images de l'ensemble de données MNIST sont centrées et mises à l'échelle, aucune opération de convolution n'est effectuée. Toutes les tâches de classification partagent le même réseau, utilisant la descente de gradient stochastique sans impulsion, et les autres paramètres sont les mêmes que ceux testés sur l'ensemble de données ImageNet.

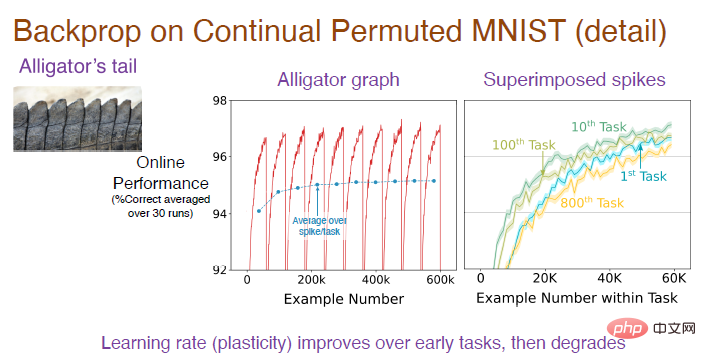
Remarque : L'image du milieu est le résultat moyen après 30 exécutions indépendantes sur la séquence de tâches. Chaque tâche comporte 6 000 échantillons. Puisqu'il s'agit d'une tâche de classification, la précision de la supposition aléatoire au début est de 10 %. les règles d'organisation des images, la précision de la prédiction augmentera progressivement, mais après avoir changé de tâche, la précision chute à 10 %, de sorte que la tendance globale fluctue constamment. L'image de droite montre l'effet d'apprentissage du modèle sur chaque tâche. La précision initiale est de 0. Au fil du temps, l'effet s'améliore progressivement. La précision sur la 10ème tâche est meilleure que sur la 1ère tâche, mais la précision diminue sur la 100ème tâche et la précision sur la 800ème tâche est encore inférieure à la première.

Afin de comprendre l'ensemble du processus, nous devons nous concentrer sur l'analyse de la précision de la partie convexe, puis en faire la moyenne pour obtenir la courbe bleue de l'image intermédiaire. On voit clairement que la précision augmentera progressivement au début puis se stabilisera jusqu'à la 100ème tâche. Alors pourquoi la précision chute-t-elle fortement à la 800e tâche ?

Ensuite, nous avons essayé différentes valeurs de pas sur davantage de séquences de tâches pour observer davantage leurs effets d'apprentissage. Les résultats sont les suivants :

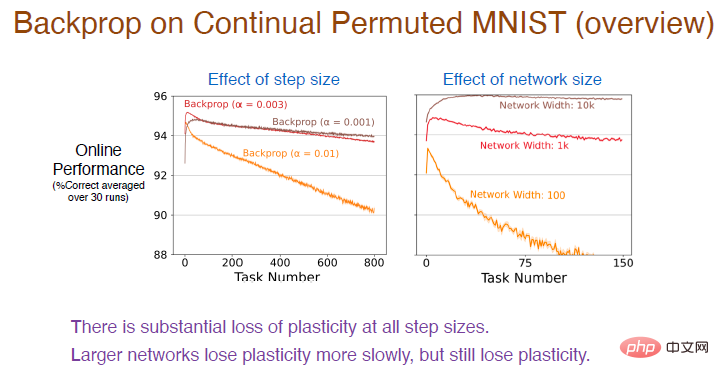
Légende : La courbe rouge utilise la même valeur de pas que l'expérience précédente. La précision diminue en effet régulièrement, et la perte de plasticité est relativement importante.

Dans le même temps, plus le taux d'apprentissage est élevé, plus la plasticité diminue rapidement. Il existe une énorme perte de plasticité pour toutes les valeurs de pas. De plus, le nombre de neurones dans la couche cachée affectera également la précision. Le nombre de neurones dans la courbe brune est de 10 000. En raison de la capacité d'ajustement améliorée du réseau neuronal, la précision diminuera très lentement à ce moment-là. il y aura toujours une perte de plasticité, mais plus la taille du réseau est grande, plus la précision diminuera. Plus la taille est petite, plus la plasticité diminue rapidement.

Alors, depuis l'intérieur du réseau neuronal, pourquoi une perte de plasticité se produit-elle ?

La photo ci-dessous explique pourquoi. On constate qu'une proportion trop élevée de neurones « morts », un poids excessif des neurones et une perte de diversité neuronale sont autant de causes de perte de plasticité.

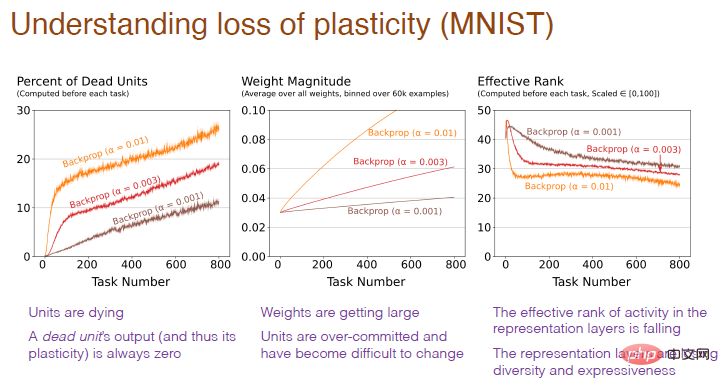
Note du graphique : L'axe horizontal représente toujours le numéro de tâche. L'axe vertical de la première image représente le pourcentage de neurones "morts". Les neurones "morts" font référence à ceux dont la sortie et le gradient sont toujours. 0 Neurones, ne prédisent plus la plasticité du réseau. L'axe vertical du deuxième graphique représente le poids. L'axe vertical du troisième graphique représente le niveau effectif du nombre de neurones cachés restants.

2 Limitations des méthodes existantes

Nous analysons si les méthodes d'apprentissage en profondeur existantes autres que la rétropropagation aideront à maintenir la plasticité.

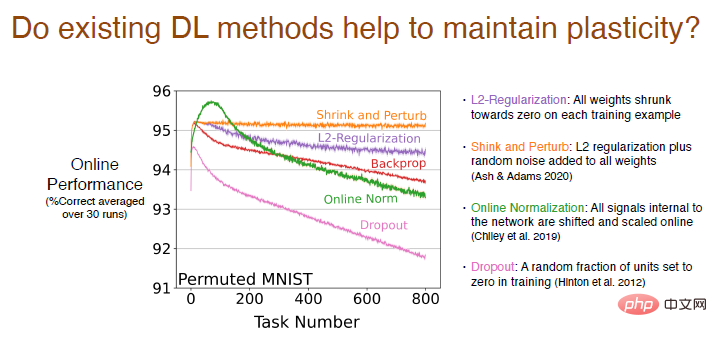
Les résultats montrent que la méthode de régularisation L2 réduira la perte de plasticité, réduisant ainsi les poids à 0, afin qu'elle puisse être ajustée dynamiquement et maintenir la plasticité.

Les méthodes de retrait et de perturbation sont similaires à la régularisation L2. En même temps, du bruit aléatoire est ajouté à tous les poids pour augmenter la diversité, et il n'y a pratiquement aucune perte de plasticité.

Nous avons également essayé d'autres méthodes de standardisation en ligne. Les résultats étaient relativement bons au début, mais la perte de plasticité était importante à mesure que l'apprentissage se poursuivait. Les performances de la méthode Dropout sont encore pires. Nous avons mis aléatoirement une partie des neurones à 0 pour le recyclage et avons constaté que la perte de plasticité augmentait fortement.

Diverses méthodes auront également un impact sur la structure interne du réseau neuronal. L'utilisation d'une méthode de régularisation augmentera le pourcentage de neurones « morts », car lors du processus de réduction des poids à 0, s'ils restent à 0, la sortie sera 0 et les neurones « mourront ». Et le rétrécissement et la perturbation ajoutent du bruit aléatoire aux poids, de sorte qu'il n'y a pas trop de neurones « morts ». La méthode de normalisation comporte également beaucoup de neurones "morts" et elle semble aller dans la mauvaise direction, et Dropout est similaire.

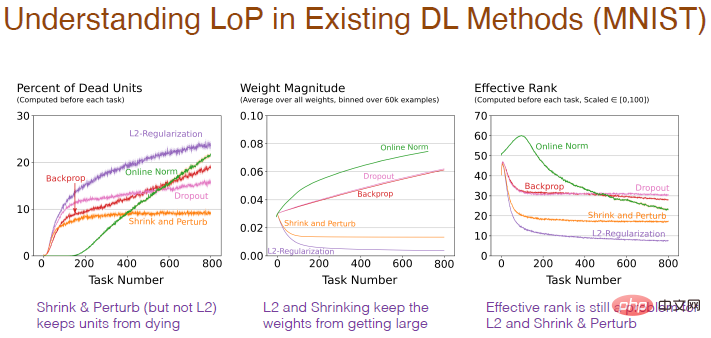
Le résultat de l'évolution du poids avec le nombre de tâches est plus raisonnable. L'utilisation de la régularisation obtiendra un très faible poids et la perturbation ajoutera du bruit sur la base de la régularisation, tandis que la standardisation rendra le résultat plus raisonnable. le poids devient plus grand. Cependant, pour la régularisation, la contraction et la perturbation de L2, le niveau effectif du nombre de neurones cachés est relativement faible, ce qui indique que ses performances en matière de maintien de la diversité sont médiocres, ce qui constitue également un problème.

Problème de régression à évolution lente (SCR)

Toutes nos idées et algorithmes sont dérivés du Problème de régression à évolution lenteExpériences, qui est un nouveau problème idéalisé axé sur l'apprentissage continu.

Dans cette expérience, notre objectif est d'atteindre la fonction objectif formée par un réseau neuronal monocouche avec des poids aléatoires, et les neurones de la couche cachée sont 100 neurones à seuil linéaire.

Nous ne faisons pas de classification, nous générons simplement un nombre, c'est donc un problème de régression. Toutes les 10 000 étapes d'entraînement, nous sélectionnons 1 bit parmi les 15 derniers bits de l'entrée à inverser, il s'agit donc d'une fonction objectif qui évolue lentement.

Notre solution est d'utiliser la même structure de réseau, avec une seule couche cachée de neurones, tout en s'assurant que la fonction d'activation est différentiable, mais nous aurons 5 neurones cachés. Ceci est similaire à RL. La plage d'exploration par l'agent est beaucoup plus petite que l'environnement interactif, il ne peut donc effectuer qu'un traitement approximatif. À mesure que la fonction objectif change, essayez de modifier la valeur approximative, ce qui facilitera la tâche. quelques expériences systématiques.

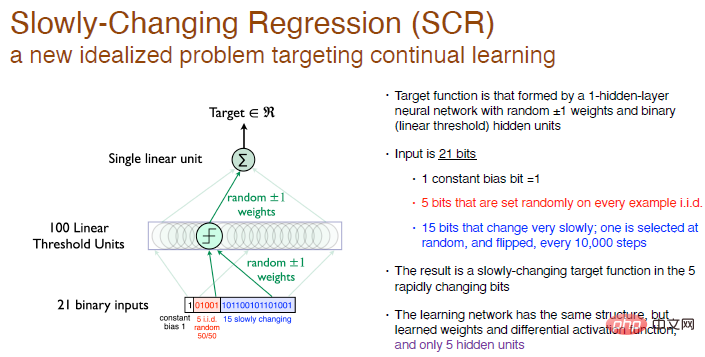
Légende : L'entrée est un nombre binaire aléatoire de 21 bits, le premier bit est l'écart constant d'entrée avec une valeur de 1, les 5 bits du milieu sont des nombres aléatoires indépendants et identiquement distribués, et l'autre 15 bits changent lentement Constant, la sortie est un nombre réel. Les poids sont randomisés à 0 et peuvent être choisis au hasard pour être +1 ou -1.

Nous avons étudié plus en détail l'impact de la modification des valeurs de pas et des fonctions d'activation sur l'effet d'apprentissage. Par exemple, les fonctions d'activation tanh, sigmoïde et relu sont utilisées ici :

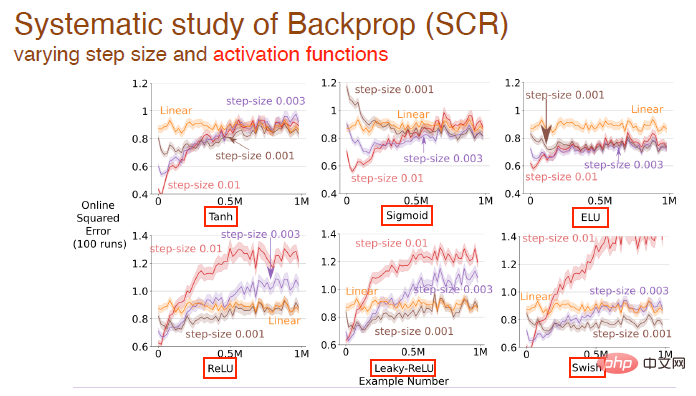
et le formulaire de fonction d'activation. convient à tous les algorithmes Influence de l'effet d'apprentissage :

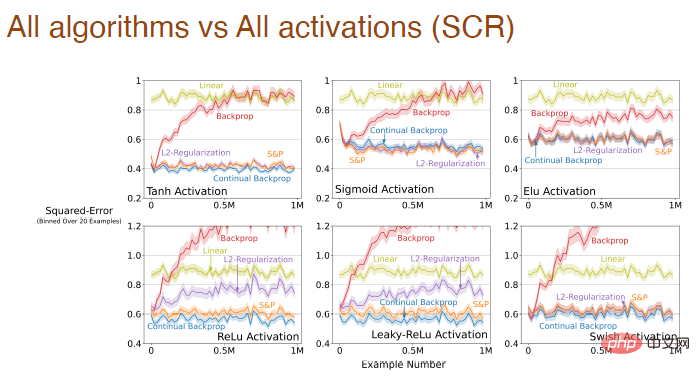
Lorsque la taille du pas et la fonction d'activation changent en même temps, nous avons également effectué une analyse systématique de l'impact de la rétro-propagation d'Adam :

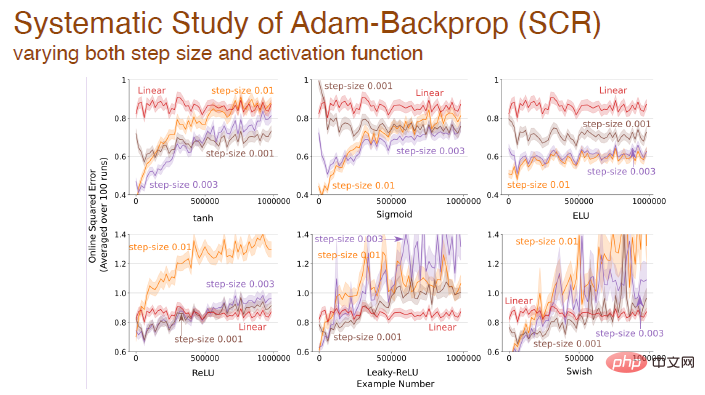
Enfin, en utilisant différents Après avoir activé la fonction, l'erreur change entre différents algorithmes basés sur le mécanisme d'Adam :

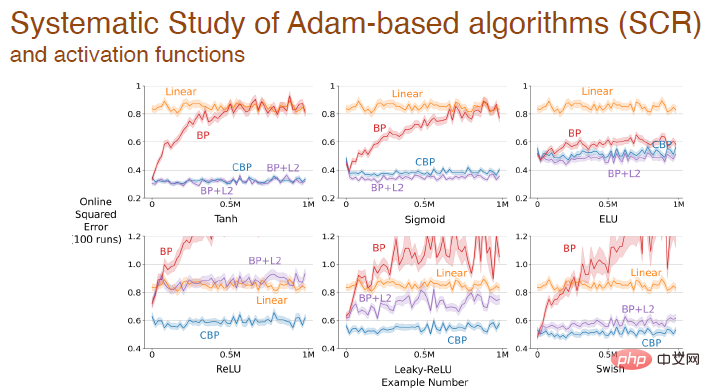
Les résultats expérimentaux ci-dessus montrent que les méthodes d'apprentissage en profondeur ne sont plus adaptées à l'apprentissage continu En cas de rencontre. nouveaux problèmes, apprentissage Le processus deviendra très lent et l'avantage de la profondeur ne sera pas reflété. Les méthodes standardisées d’apprentissage profond ne conviennent qu’à un apprentissage ponctuel. Nous devons améliorer les méthodes d’apprentissage profond pour permettre leur utilisation pour l’apprentissage continu.

3 Rétropropagation continue

L'algorithme de rétropropagation convolutionnelle sera-t-il lui-même un bon algorithme d'apprentissage continu ?

Nous ne le pensons pas.

L'algorithme de rétropropagation par convolution contient principalement deux aspects : l'initialisation avec de petits poids aléatoires et la descente de gradient à chaque pas de temps. Bien qu'il génère de petits nombres aléatoires au début pour initialiser les poids, il ne se répète pas. Idéalement, nous souhaiterions peut-être un algorithme d’apprentissage capable d’effectuer des calculs similaires à tout moment.

Alors, comment faire en sorte que l'algorithme de rétropropagation convolutionnelle apprenne en continu ?

Le moyen le plus simple est de réinitialiser de manière sélective, par exemple, après avoir effectué plusieurs tâches. Mais en même temps, réinitialiser l’ensemble du réseau n’est peut-être pas raisonnable en cas d’apprentissage continu, car cela signifie que le réseau neuronal oublie tout ce qu’il a appris. Il est donc préférable d'initialiser sélectivement une partie du réseau neuronal, par exemple en réinitialisant certains neurones "morts", ou en triant le réseau neuronal en fonction de son utilité et en réinitialisant les neurones ayant une utilité moindre.

L'idée d'une initialisation sélectionnée au hasard est liée à la méthode de génération et de test proposée par Mahmood et Sutton en 2012. Il suffit de générer quelques neurones et de tester leur fonctionnalité. L'algorithme de rétropropagation continue établit la connexion entre ces deux. notions de pont. La méthode de génération et de test présente certaines limites, utilisant une seule couche cachée et un seul neurone de sortie, nous l'étendons à un réseau multicouche qui peut être optimisé avec certaines méthodes d'apprentissage profond.

Nous envisageons d'abord de

configurer le réseau en plusieurs couches au lieu d'une seule sortie. Des travaux antérieurs mentionnaient le concept d'utilité. Puisqu'il n'y a qu'un seul poids, cette utilité n'est qu'un concept au niveau du poids. Cependant, nous avons plusieurs poids. La généralisation la plus simple consiste à considérer l'utilité au niveau de la somme des poids.

Une autre idée est de

considérer l'activité des fonctionnalités au lieu de simplement les poids de sortie, afin que nous puissions multiplier la somme des poids par la fonction d'activation moyenne des fonctionnalités, attribuant ainsi différentes proportions. Nous espérons concevoir des algorithmes capables de continuer à apprendre et à fonctionner rapidement. Nous prenons également en compte la plasticité des fonctionnalités lors du calcul de l'utilité. Enfin, la contribution moyenne des fonctionnalités est transférée au biais de sortie, réduisant ainsi l'impact de la suppression des fonctionnalités.

Il y a deux directions principales pour des améliorations futures : (1) Nous devons

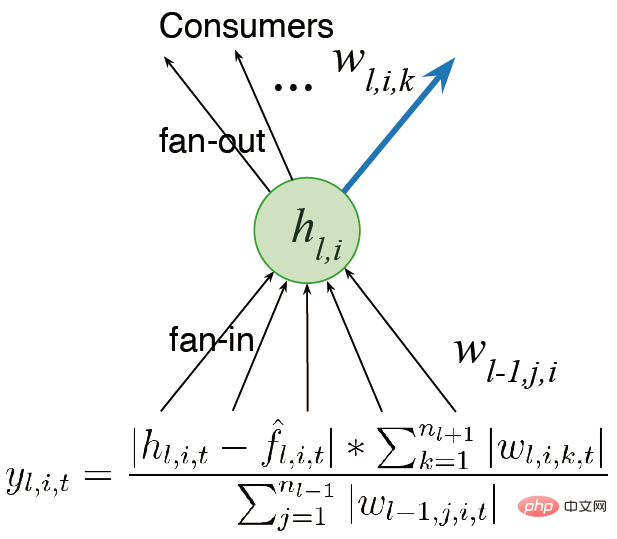
faire une mesure globale de l'utilité, mesurer l'impact des neurones sur l'ensemble de la fonction représentée, et pas seulement se limiter aux poids d'entrée, de sortie mesures locales telles que les poids et les fonctions d'activation ; (2) Nous devons encore améliorer le générateur. Actuellement, nous échantillonnons uniquement à partir de la distribution initiale pour l'initialisation, et nous devons également explorer des méthodes d'initialisation qui peuvent améliorer les performances. Alors, dans quelle mesure la rétropropagation continue réussit-elle à maintenir la plasticité ?

Les résultats expérimentaux montrent que la rétropropagation continue, entraînée à l'aide de l'ensemble de données MNIST aligné en ligne, maintient pleinement la plasticité.

La courbe bleue dans la figure ci-dessous montre ce résultat.

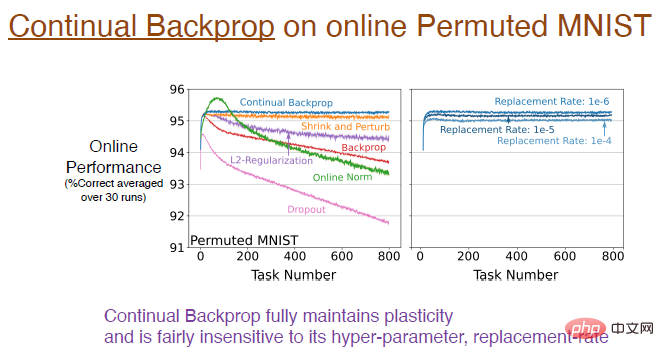Légende : L'image de droite montre l'impact de différents taux de remplacement sur l'apprentissage continu. Par exemple, un taux de remplacement de 1e-6 signifie remplacer 1/1000000 de représentations à chaque pas de temps. Autrement dit, en supposant qu’il y ait 2 000 caractéristiques, un neurone sera remplacé dans chaque couche toutes les 500 étapes. Cette vitesse de mise à jour est très lente, le taux de remplacement n'est donc pas très sensible aux hyperparamètres et n'affectera pas de manière significative l'effet d'apprentissage.

Ensuite, nous devons étudier l'impact de la rétropropagation continue sur la structure interne du réseau neuronal. Il n'y a presque pas de neurones "morts" en rétropropagation continue.

Étant donné que l'utilitaire prend en compte l'activation moyenne des fonctionnalités, si un neurone "meurt", il sera immédiatement remplacé. Et comme nous continuons à remplacer les neurones, nous obtenons de nouveaux neurones avec un poids plus faible. Étant donné que les neurones sont initialisés de manière aléatoire, ils conservent en conséquence une représentation et une diversité plus riches.

Ainsi, la rétropropagation continue résout tous les problèmes causés par le manque de plasticité sur l'ensemble de données MNIST.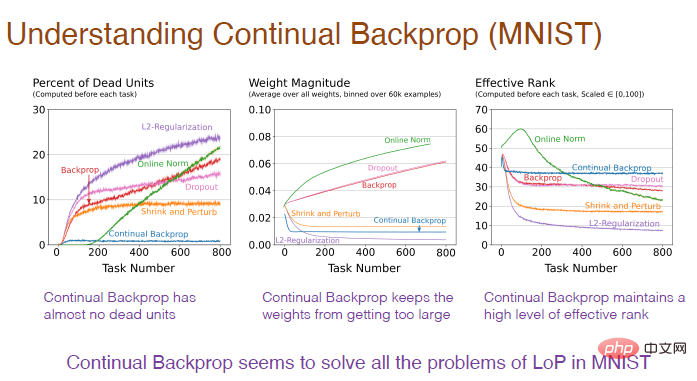

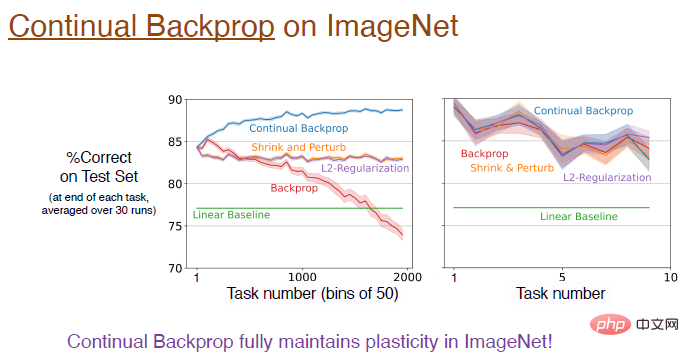
Alors, la rétropropagation continue peut-elle être étendue à des réseaux neuronaux convolutifs plus profonds ?

La réponse est oui ! Sur l'ensemble de données ImageNet, la rétropropagation continue a entièrement préservé la plasticité et la précision finale du modèle était d'environ 89 %. En fait, dans la phase initiale de formation, les performances de ces algorithmes sont équivalentes. Comme mentionné précédemment, le taux de remplacement évolue très lentement, et l'approximation n'est meilleure que lorsque le nombre de tâches est suffisamment grand.

Nous prenons ici le problème de la "Fourmi glissante" comme exemple pour montrer les résultats expérimentaux de l'apprentissage par renforcement.

Le problème « Slippery Ant » est une extension du problème du renforcement non stationnaire et est fondamentalement similaire à l'environnement PyBullet, sauf que la friction entre le sol et l'agent change tous les 10 millions de pas. Nous avons implémenté une version d'apprentissage continu de l'algorithme PPO basée sur la rétropropagation continue, qui peut être initialisée de manière sélective. Les résultats de la comparaison entre l'algorithme PPO et l'algorithme PPO continu sont les suivants.

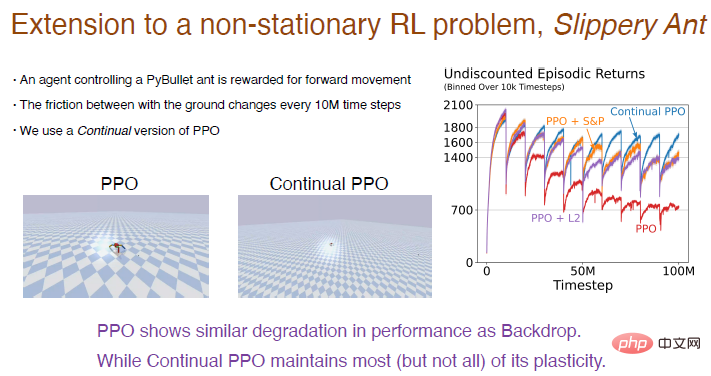
Illustration : L'algorithme PPO fonctionne bien au début, mais au fur et à mesure que l'entraînement progresse, les performances continuent de baisser, ce qui sera atténué après l'introduction de l'algorithme L2 et de l'algorithme de retrait et de perturbation. L’algorithme PPO continu a relativement bien fonctionné, conservant l’essentiel de la plasticité.

Fait intéressant, l'agent formé par l'algorithme PPO ne peut que lutter pour marcher, mais l'agent formé par l'algorithme PPO en continu peut courir très loin.

4 Conclusion

Les réseaux d'apprentissage profond sont principalement optimisés pour un apprentissage ponctuel, dans le sens où ils peuvent échouer complètement lorsqu'ils sont utilisés pour un apprentissage continu. Les méthodes d'apprentissage en profondeur telles que la normalisation et DropOut peuvent ne pas être utiles pour l'apprentissage continu, mais apporter quelques petites améliorations sur cette base, telles que la rétropropagation continue, peut être très efficace.

La rétropropagation continue trie les caractéristiques du réseau en fonction de l'utilité des neurones, en particulier pour les réseaux neuronaux récurrents, il peut y avoir davantage d'améliorations dans la méthode de tri.

L'algorithme d'apprentissage par renforcement utilise l'idée d'itération de politiques. Bien que des problèmes d'apprentissage continu existent, le maintien de la plasticité des réseaux d'apprentissage profond ouvre d'énormes nouvelles possibilités pour le RL et le RL basé sur des modèles.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!