L'apprentissage par renforcement découvre l'algorithme de multiplication matricielle, DeepMind apparaît en couverture de Nature et lance AlphaTensor

Les algorithmes aident les mathématiciens à effectuer des opérations de base depuis des milliers d'années. Il y a longtemps, les anciens Égyptiens ont inventé un algorithme permettant de multiplier deux nombres sans avoir recours à une table de multiplication. Le mathématicien grec Euclide a décrit un algorithme permettant de calculer le plus grand diviseur commun, encore utilisé aujourd'hui. Au cours de l’âge d’or islamique, le mathématicien persan Muhammad ibn Musa al-Khwarizmi a conçu un nouvel algorithme pour résoudre des équations linéaires et quadratiques qui aurait un impact profond sur les recherches ultérieures.

En fait, il existe un dicton sur l'émergence du mot algorithme : le mot al-Khwarizmi au nom du mathématicien persan Muhammad ibn Musa al-Khwarizmi est traduit en latin par Algoritmi, ce qui conduit à l'introduction de algorithme 1. mot. Cependant, même si aujourd'hui nous sommes très familiers avec les algorithmes, nous pouvons les apprendre en classe et les rencontrer souvent dans le domaine de la recherche scientifique. Il semble que la société tout entière utilise des algorithmes, mais le processus de découverte de nouveaux algorithmes est très difficile. . ​

Désormais, DeepMind utilise l'IA pour découvrir de nouveaux algorithmes.

Dans l'article de couverture du dernier numéro de Nature "Découverte d'algorithmes de multiplication matricielle plus rapides avec apprentissage par renforcement", DeepMind a proposé AlphaTensor et a déclaré qu'il est le premier à découvrir des algorithmes nouveaux, efficaces et prouvables pour des tâches de base telles que la multiplication matricielle. . Système d'intelligence artificielle avec algorithme correct. En termes simples, utiliser AlphaTensor vous permet de découvrir de nouveaux algorithmes. La recherche met en lumière un problème mathématique non résolu vieux de 50 ans : trouver le moyen le plus rapide de multiplier deux matrices.

• Adresse papier : https://www.nature.com/articles/s41586-022-05172-4
• G Adresse itHub : https:// /github.com/deepmind/alphatensor ​

AlphaTensor est construit sur AlphaZero, un agent qui peut battre les humains dans des jeux de société comme les échecs, le Go et le shogi. Ce travail démontre la transition d'AlphaZero d'une utilisation pour des jeux à une utilisation pour la première fois pour résoudre des problèmes mathématiques non résolus. ​​

Multiplication matricielle

La multiplication matricielle est l'une des opérations les plus simples en algèbre et est généralement enseignée dans les cours de mathématiques du secondaire. Mais en dehors de la salle de classe, cette humble opération mathématique a eu un impact énorme dans le monde numérique contemporain et est omniprésente dans l’informatique moderne.

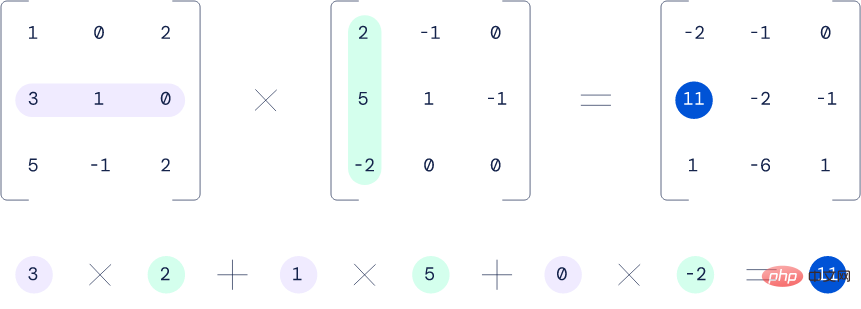
Exemple de multiplication de deux matrices 3x3. ​

Vous n'avez peut-être pas remarqué que la multiplication matricielle est cachée partout dans nos vies, comme le traitement d'images dans les smartphones, la reconnaissance des commandes vocales, la génération de graphiques pour les jeux informatiques, etc. Tout fonctionne derrière. Les entreprises du monde entier sont prêtes à consacrer beaucoup de temps et d’argent au développement de matériel informatique pour résoudre efficacement la multiplication matricielle. Par conséquent, même de petites améliorations de l’efficacité de la multiplication matricielle peuvent avoir des effets étendus.

Depuis des siècles, les mathématiciens considèrent l'algorithme de multiplication matricielle standard comme l'algorithme le plus efficace. Mais en 1969, le mathématicien allemand Volken Strassen a choqué le monde mathématique en prouvant qu’il existait bel et bien un meilleur algorithme.

En comparant l'algorithme standard avec l'algorithme de Strassen, ce dernier nécessite une opération de multiplication de moins, soit 7 fois, tandis que le premier en nécessite 8 fois, et l'efficacité globale est grandement améliorée. ​

En étudiant de très petites matrices (taille 2x2), Strassen a découvert une manière astucieuse de combiner les termes de la matrice pour produire un algorithme plus rapide. Au cours des décennies suivantes, les chercheurs ont étudié des matrices plus grandes, et même la recherche d’une méthode efficace pour multiplier des matrices 3x3 n’a pas encore été résolue.

Une nouvelle recherche de DeepMind explore comment la technologie moderne de l’IA favorise la découverte automatique de nouveaux algorithmes de multiplication matricielle. Basé sur les progrès de l'intuition humaine, l'algorithme découvert par AlphaTensor est plus efficace que de nombreuses méthodes SOTA pour des matrices plus grandes. L’étude montre que les algorithmes conçus par l’IA surpassent ceux conçus par les humains, ce qui constitue une avancée importante dans le domaine de la découverte d’algorithmes.

Le processus et les progrès de l'automatisation de la découverte d'algorithmes

Convertissez d'abord le problème de la découverte d'algorithmes efficaces pour la multiplication matricielle en un jeu solo. Parmi eux, board est un tenseur tridimensionnel (tableau de nombres) utilisé pour mesurer l'exactitude de l'algorithme actuel. Grâce à un ensemble de mouvements autorisés correspondant aux instructions de l'algorithme, le joueur tente de modifier le tenseur et de remettre ses entrées à zéro.

Lorsque le joueur parvient à faire cela, un algorithme de multiplication matricielle prouvée correct est généré pour n'importe quelle paire de matrices, et son efficacité est mesurée par le nombre d'étapes prises pour mettre à zéro le tenseur.

Ce jeu est très difficile et le nombre d'algorithmes possibles à considérer est bien supérieur au nombre d'atomes dans l'univers, même pour un cas aussi petit que la multiplication matricielle. Comparé au jeu de Go, qui constitue un défi d'IA depuis des décennies, le jeu propose 30 ordres de grandeur de mouvements possibles en plus par mouvement (un paramètre pris en compte par DeepMind était 10^33+.)

Pour résoudre ce problème avec DeepMind, il a fallu a développé plusieurs composants clés pour relever les défis d'un domaine très différent des jeux traditionnels, notamment une nouvelle architecture de réseau neuronal qui intègre des biais inductifs spécifiques à un problème, un programme pour générer des données synthétiques utiles et une méthode pour exploiter les symétries des problèmes.

Ensuite, DeepMind a formé un agent d'apprentissage par renforcement, AlphaTensor, pour jouer au jeu, en commençant sans aucune connaissance des algorithmes de multiplication matricielle existants. En apprenant, AlphaTensor s'améliore progressivement au fil du temps, redécouvrant des algorithmes matriciels historiquement rapides (tels que l'algorithme de Strassen) et découvrant des algorithmes plus rapides que ceux connus auparavant.

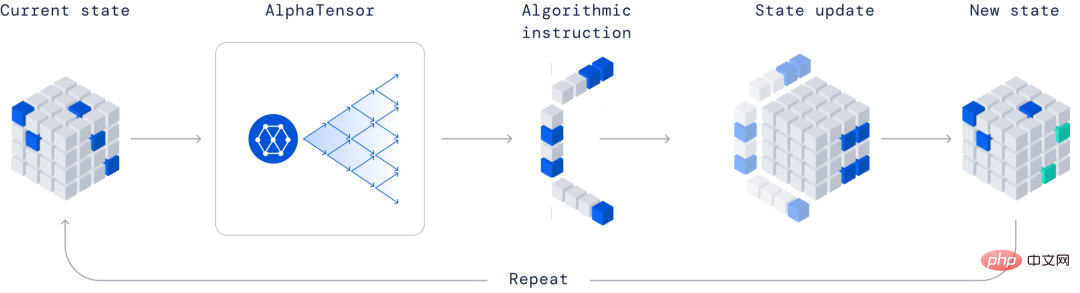
AlphaTensor Un jeu solo où le but est de trouver le bon algorithme de multiplication matricielle. L'état du jeu est un tableau cubique de nombres (le gris représente 0, le bleu représente 1 et le vert représente - 1) qui représente le travail restant à effectuer. ​

Par exemple, si l'algorithme traditionnel enseigné à l'école peut multiplier des matrices 4x5 et 5x5 en utilisant 100 multiplications, l'ingéniosité humaine peut réduire ce nombre à 80 fois. En comparaison, l'algorithme découvert par AlphaTensor accomplit la même opération en utilisant seulement 76 multiplications, comme le montre l'image ci-dessous.

En plus des exemples ci-dessus, l'algorithme découvert par AlphaTensor améliore également pour la première fois l'algorithme du second ordre de Strassen dans un corps fini. Ces algorithmes de multiplication de petites matrices peuvent être utilisés comme primitives pour multiplier des matrices plus grandes de n'importe quelle taille.

AlphaTensor a également découvert un ensemble diversifié d'algorithmes de complexité SOTA, avec jusqu'à des milliers d'algorithmes de multiplication matricielle de chaque taille, indiquant que l'espace des algorithmes de multiplication matricielle est plus riche qu'on ne le pensait auparavant.

Les algorithmes de cet espace riche ont différentes propriétés mathématiques et pratiques. Profitant de cette diversité, DeepMind a optimisé AlphaTensor pour découvrir spécifiquement des algorithmes qui s'exécutent rapidement sur un matériel donné (par exemple, le GPU Nvidia V100, Google TPU v2). Ces algorithmes effectuent de grandes multiplications matricielles 10 à 20 % plus rapidement que les algorithmes couramment utilisés sur le même matériel, démontrant la flexibilité d'AlphaTensor dans l'optimisation d'objectifs arbitraires.

AlphaTensor a une cible qui correspond au temps d'exécution de l'algorithme. Lorsque l'algorithme de multiplication matricielle correct est découvert, il est évalué sur le matériel spécifié, puis renvoyé à AlphaTensor pour apprendre un algorithme plus efficace sur le matériel spécifié.

Impact sur les recherches et applications futures

D’un point de vue mathématique, les résultats de DeepMind peuvent guider de nouvelles recherches sur la théorie de la complexité, qui visent à identifier les algorithmes les plus rapides pour résoudre des problèmes informatiques. AlphaTensor nous aide à approfondir notre compréhension de la richesse des algorithmes de multiplication matricielle en explorant l'espace des algorithmes possibles plus efficacement que les méthodes précédentes.

De plus, étant donné que la multiplication matricielle est un élément essentiel de nombreuses tâches informatiques telles que l'infographie, les communications numériques, la formation aux réseaux neuronaux et le calcul scientifique, les algorithmes découverts par AlphaTensor peuvent améliorer considérablement l'efficacité informatique dans ces domaines.

Bien que cet article se concentre uniquement sur le problème spécifique de la multiplication matricielle, DeepMind espère inciter davantage de personnes à utiliser l'IA pour guider la découverte d'algorithmes pour d'autres tâches informatiques de base. De plus, les recherches de DeepMind montrent également que le puissant algorithme d’AlphaZero va bien au-delà du domaine des jeux traditionnels et peut aider à résoudre des problèmes ouverts dans le domaine des mathématiques.

À l'avenir, DeepMind espère utiliser davantage l'intelligence artificielle pour aider la société à résoudre certains des défis les plus importants en mathématiques et en sciences sur la base de leurs recherches.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!