Maison >développement back-end >Tutoriel Python >Quel est le principe d'implémentation des entiers dans la machine virtuelle Python ?
Quel est le principe d'implémentation des entiers dans la machine virtuelle Python ?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-18 09:18:481431parcourir
Structure des données
La structure des données d'implémentation du type int à l'intérieur de cpython est la suivante :
typedef struct _longobject PyLongObject;
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
#define PyObject_VAR_HEAD PyVarObject ob_base;
typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
_PyObject_HEAD_EXTRA
Py_ssize_t ob_refcnt;
struct _typeobject *ob_type;
} PyObject;La structure de données ci-dessus est représentée graphiquement comme indiqué ci-dessous :
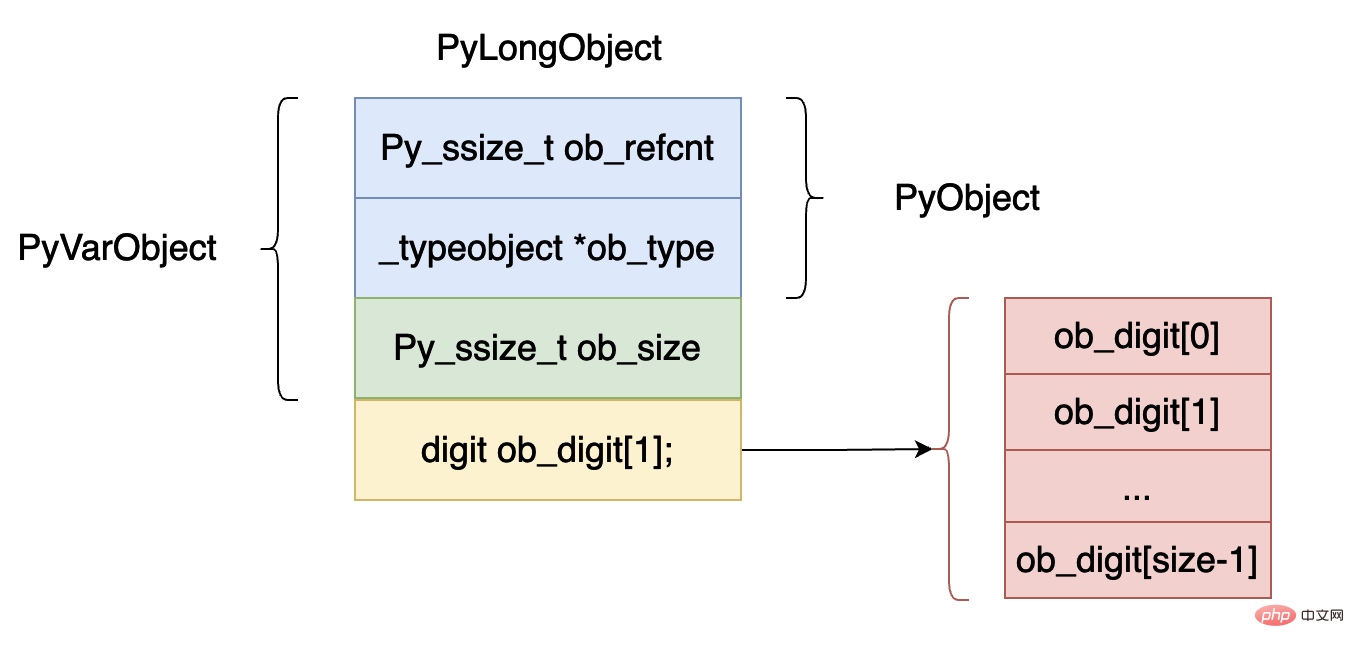
ob_refcnt, qui représente la référence de l'objet. Le nombre de comptes est très utile pour le garbage collection. Plus tard, nous analyserons en profondeur la partie garbage collection de la machine virtuelle.
ob_type indique le type de données de cet objet. En python, il est parfois nécessaire de juger du type de données des données. Par exemple, les deux mots clés isinstance et type utiliseront ce champ.
ob_size, ce champ indique combien d'éléments il y a dans ce tableau d'objets entiers ob_digit. Le type
digit est en fait une définition de macro du type uint32_t, représentant des données entières de 32 bits.
Analyse approfondie de la sémantique des champs PyLongObject
Tout d'abord, nous savons que les entiers en python ne déborderont pas, c'est pourquoi PyLongObject utilise des tableaux. Dans l'implémentation interne de cpython, les entiers incluent 0, des nombres positifs et des nombres négatifs. À ce sujet, il existe les réglementations suivantes dans cpython :
ob_size, qui stocke la longueur du tableau lorsque ob_size est supérieur à 0, il stocke les nombres positifs Lorsque ob_size est inférieur à 0, un nombre négatif est stocké.
ob_digit, stocke la valeur absolue de l'entier. Comme nous l'avons mentionné précédemment, ob_digit est une donnée de 32 bits, mais seuls les 30 premiers bits sont utilisés en interne dans Python, juste pour éviter les problèmes de débordement.
Utilisons quelques exemples pour comprendre en profondeur les règles ci-dessus :
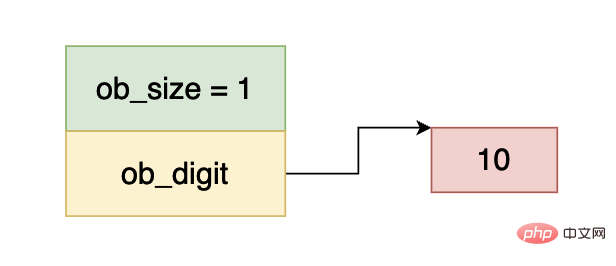
Dans l'image ci-dessus, ob_size est supérieur à 0, indiquant que ce nombre est un nombre positif, et ob_digit pointe vers une donnée int32, la valeur du nombre est égale à 10, donc le nombre ci-dessus représente l'entier 10.
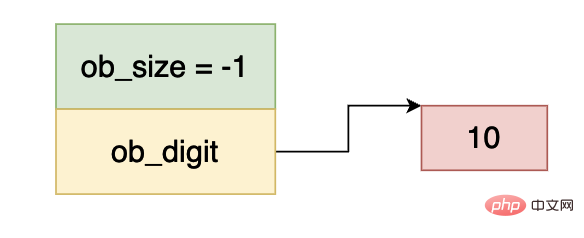
De même, ob_size est inférieur à 0 et ob_digit est égal à 10, donc les données dans l'image ci-dessus représentent -10.

Ce qui précède est un exemple d'une longueur de tableau ob_digit de 2. Les données représentées ci-dessus sont les suivantes :
1⋅20+1⋅21+1⋅22+. .. +1⋅229+0⋅230+0⋅231+1⋅232
Parce que pour chaque élément du tableau nous n'utilisons que les 30 premiers bits, donc jusqu'au deuxième entier les données correspondent à 230. Vous pouvez comprendre l’ensemble du processus de calcul sur la base des résultats ci-dessus.

Ce qui précède est très simple :
−(1⋅20+1⋅21+1⋅22+...+1⋅229+0&sdot ; 230+0⋅231+1⋅232)
Petit pool d'entiers
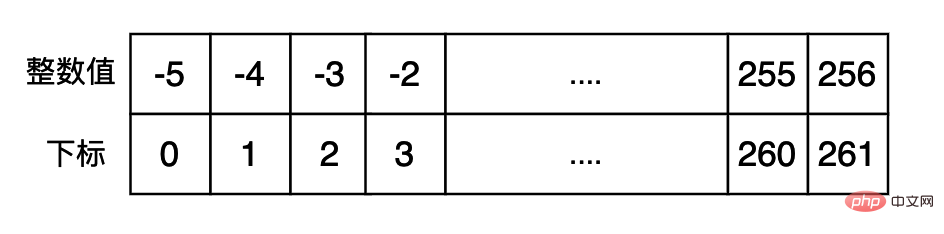
Afin d'éviter de créer fréquemment des entiers couramment utilisés et d'accélérer l'exécution du programme, nous pouvons utiliser du cache d'entiers couramment utilisés. d'abord et renvoyez les données directement si nécessaire. Le code pertinent dans cpython est le suivant : (L'intervalle des données mises en cache dans le petit pool d'entiers est [-5, 256])
#define NSMALLPOSINTS 257 #define NSMALLNEGINTS 5 static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];
Nous utilisons le code suivant pour tester si le petit pool d'entiers est utilisé Data, si elle est utilisée, la valeur de retour de leur id() est la même pour les données du petit pool d'entiers. La fonction intégrée id renvoie l'adresse mémoire de l'objet Python.
>>> a = 1 >>> b = 2 >>> c = 1 >>> id(a), id(c) (4343136496, 4343136496) >>> a = -6 >>> c = -6 >>> id(a), id(c) (4346020624, 4346021072) >>> a = 257 >>> b = 257 >>> id(a), id(c) (4346021104, 4346021072) >>>
Ce que nous pouvons voir à partir des résultats ci-dessus, c'est que pour les valeurs dans l'intervalle [-5, 256], la valeur de retour de id est effectivement la même, et la valeur de retour en dehors de cet intervalle est différente.
On peut également implémenter une petite astuce avec cette fonctionnalité, qui consiste à trouver l'espace mémoire occupé par un objet PyLongObject, car on peut utiliser la première adresse mémoire des deux données -5 et 256, puis soustraire ces adresses Get. la taille de l'espace mémoire occupé par 261 PyLongObjects (notez que bien qu'il y ait 262 données dans le petit pool d'entiers, les dernières données sont la première adresse de la mémoire, pas la dernière adresse, il n'y a donc que 261 données), de sorte que nous pouvons trouver une taille de mémoire de l'objet PyLongObject.
>>> a = -5 >>> b = 256 >>> (id(b) - id(a)) / 261 32.0 >>>
D'après la sortie ci-dessus, nous pouvons voir qu'un objet PyLongObject occupe 32 octets. Nous pouvons utiliser le programme C suivant pour afficher l'espace mémoire réel occupé par un PyLongObject.
#include "Python.h"
#include <stdio.h>
int main()
{
printf("%ld\n", sizeof(PyLongObject));
return 0;
}Le résultat du programme ci-dessus est le suivant :

Les deux résultats ci-dessus sont égaux, donc notre idée est également vérifiée.
Le code de base pour obtenir des données du petit pool d'entiers est le suivant :
static PyObject *
get_small_int(sdigit ival)
{
PyObject *v;
assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
Py_INCREF(v);
return v;
}整数的加法实现
如果你了解过大整数加法就能够知道,大整数加法的具体实现过程了,在 cpython 内部的实现方式其实也是一样的,就是不断的进行加法操作然后进行进位操作。
#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的绝对值
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
// 首先获得两个整型数据的 size
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
// 确保 a 保存的数据 size 是更大的
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 创建一个新的 PyLongObject 对象,而且数组的长度是 size_a + 1
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
// 下面就是整个加法操作的核心
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
// 将低 30 位的数据保存下来
z->ob_digit[i] = carry & PyLong_MASK;
// 将 carry 右移 30 位,如果上面的加法有进位的话 刚好可以在下一次加法当中使用(注意上面的 carry)
// 使用的是 += 而不是 =
carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
}
// 将剩下的长度保存 (因为 a 的 size 是比 b 大的)
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
// 最后保存高位的进位
z->ob_digit[i] = carry;
return long_normalize(z); // long_normalize 这个函数的主要功能是保证 ob_size 保存的是真正的数据的长度 因为可以是一个正数加上一个负数 size 还变小了
}
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
PyLongObject *result;
/* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
sizeof(digit)*size. Previous incarnations of this code used
sizeof(PyVarObject) instead of the offsetof, but this risks being
incorrect in the presence of padding between the PyVarObject header
and the digits. */
if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
PyErr_SetString(PyExc_OverflowError,
"too many digits in integer");
return NULL;
}
// offsetof 会调用 gcc 的一个内嵌函数 __builtin_offsetof
// offsetof(PyLongObject, ob_digit) 这个功能是得到 PyLongObject 对象 字段 ob_digit 之前的所有字段所占的内存空间的大小
result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
size*sizeof(digit));
if (!result) {
PyErr_NoMemory();
return NULL;
}
// 将对象的 result 的引用计数设置成 1
return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
static PyLongObject *
long_normalize(PyLongObject *v)
{
Py_ssize_t j = Py_ABS(Py_SIZE(v));
Py_ssize_t i = j;
while (i > 0 && v->ob_digit[i-1] == 0)
--i;
if (i != j)
Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
return v;
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

