Les algorithmes quantiques conquièrent un nouveau type de problème !

En 1994, un mathématicien a découvert comment faire en sorte que les ordinateurs quantiques fassent des choses que les ordinateurs classiques ordinaires ne peuvent pas faire. Les travaux montrent qu'en principe, une machine basée sur les règles de la mécanique quantique peut décomposer efficacement de grands nombres en leurs principaux facteurs - une tâche très difficile pour les ordinateurs classiques, qui constituent la plupart des principes fondamentaux de la sécurité Internet actuels.

Et avec cela vient une vague d’optimisme. Peut-être, pensent les chercheurs, pourrons-nous inventer des algorithmes quantiques capables de résoudre un grand nombre de problèmes différents.

Mais les progrès sont au point mort. "C'est plutôt décevant", a déclaré Ryan O'Donnell de l'Université Carnegie Mellon. "Les gens vont dire : 'C'est génial, je suis sûr que nous allons avoir toutes sortes d'autres algorithmes incroyables', et ils le sont. non." Les scientifiques n'ont trouvé des accélérations significatives que pour une seule classe étroite de problèmes dans un ensemble standard appelé NP, ce qui signifie qu'ils disposent de solutions efficaces et vérifiables, telles que la factorisation.

C'est le cas depuis trois ans. Puis, en avril, des chercheurs ont inventé un tout nouveau type de problème que les ordinateurs quantiques devraient être capables de résoudre plus rapidement que les ordinateurs classiques. Cela implique de calculer l’entrée d’un processus mathématique complexe en se basant uniquement sur sa sortie désordonnée. Il reste à déterminer si ce problème est isolé ou s’il est le premier parmi tant d’autres.

"Il y a un sentiment d'enthousiasme", déclare Vinod Vaikuntanathan, informaticien au MIT. "Beaucoup de gens réfléchissent à ce qui existe d'autre dans les modèles mathématiques pour comprendre ce que les ordinateurs quantiques font de mieux." En règle générale, ils imaginent un modèle d’ordinateur quantique ou classique associé à un ordinateur idéal appelé oracle. Un oracle est comme une simple fonction mathématique ou un programme informatique qui prend des entrées et génère une sortie prédéterminée.

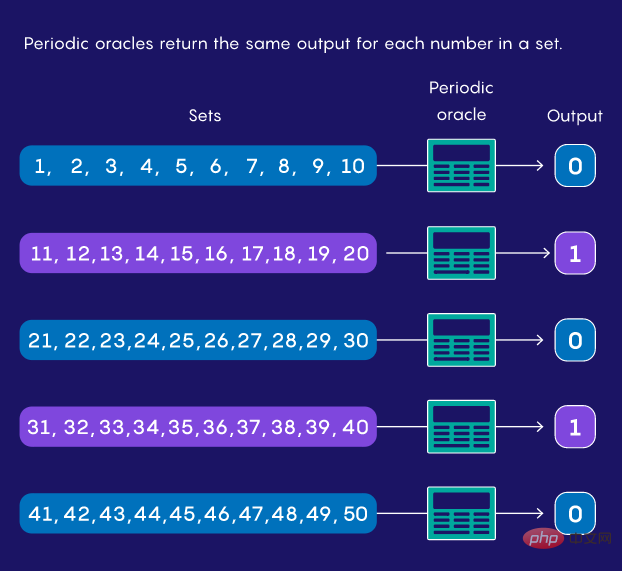
Ils peuvent avoir un comportement aléatoire, affichant « oui » si l'entrée se situe dans une plage aléatoire (par exemple, 12 à 67) et « non » sinon. Ou ils peuvent être périodiques, donc une entrée entre 1 et 10 renvoie « oui », 11 à 20 produit « non », 21 à 30 produit à nouveau « oui », et ainsi de suite.

Supposons que vous ayez une de ces prophéties périodiques, mais que vous ne connaissez pas la période. Tout ce que vous pouvez faire est de lui fournir des chiffres et de voir ce qu'il produit. À quelle vitesse un ordinateur peut-il trouver des cycles sous ces contraintes ? En 1993, Daniel Simon, alors à l'Université de Montréal, a découvert que les algorithmes quantiques pouvaient trouver des réponses à des problèmes étroitement liés plus rapidement que n'importe quel algorithme classique.

Ce résultat permet à Simon d'identifier l'un des premiers signes montrant où les ordinateurs quantiques présentent des avantages significatifs. Mais lorsqu’il soumit son article à une grande conférence, celui-ci fut rejeté. L'article a cependant éveillé l'intérêt d'un membre junior du comité du programme de la conférence, Peter Shor, qui travaillait alors aux Laboratoires Bell dans le New Jersey.

Shor a ensuite découvert qu'il pouvait modifier l'algorithme de Simon pour calculer la période de l'oracle, s'il en avait un. Puis il s'est rendu compte qu'il pouvait à nouveau modifier l'algorithme pour résoudre une équation qui se comportait comme une prophétie périodique : une équation décrivant une factorisation périodique.

Les résultats de Shor étaient historiques. L’algorithme quantique qu’il a découvert peut rapidement réduire des nombres énormes à leurs facteurs premiers qui les constituent, ce qu’aucun algorithme classique connu ne peut faire. Au cours des années suivantes, les chercheurs ont découvert d’autres algorithmes quantiques efficaces. Certains d'entre eux, comme l'algorithme de Shor, offrent même des avantages exponentiels, mais personne n'a été en mesure de prouver un avantage quantique significatif sur un problème NP non périodique.

En raison du manque de progrès, deux informaticiens, Scott Aaronson de l'Université du Texas à Austin et Andris Ambainis de l'Université de Lettonie, ont fait des observations. Les preuves de l’avantage quantique semblent toujours reposer sur des prédictions ayant une structure non aléatoire, telle que la périodicité. En 2009, ils ont émis l’hypothèse qu’il n’y aurait pas d’accélération significative pour les problèmes NP aléatoires ou non structurés ;

Leur conjecture limite les capacités des ordinateurs quantiques. Mais il dit seulement que pour certains types de problèmes NP non structurés – ceux avec des réponses par oui ou par non – il n’y a pas d’accélération significative. Cette conjecture ne s'applique pas si un problème implique de trouver une réponse quantitative plus spécifique, ce qu'on appelle un problème de recherche.

Dans cet esprit, les chercheurs Takashi Yamakawa du Laboratoire d'informatique sociale de NTT et Mark Zhandry de NTT Research et de l'Université de Princeton ont décidé d'expérimenter un problème de recherche spécifique posé par Oded Regev en 2005.

Imaginez un ensemble de girouettes pointant toutes dans la même direction. Donnez-leur à chacun une poussée mesurée et laissez la rafale influencer leur direction. Regev souhaite déterminer où ils étaient initialement pointés en fonction de leur direction finale. Des problèmes comme celui-ci sont désormais connus sous le nom d'« apprentissage des erreurs », car la poussée et le vent agissent comme des sources d'erreurs aléatoires dans la direction d'origine. Il est prouvé que les algorithmes classiques et quantiques sont difficiles à résoudre.

Yamakawa et Zhandry ont peaufiné les paramètres. Ils ont modifié la puissance de ces démarrages pour les rendre plus prévisibles. Ils ont également fait déterminer le vent par un oracle aléatoire, donc dans certains cas il est encore plus aléatoire, mais dans d'autres cas complètement endormi.

Grâce à ces modifications, les chercheurs ont découvert que l'algorithme quantique peut effectivement trouver la direction initiale. Ils ont également prouvé que tout algorithme classique doit être ralenti par un facteur exponentiel. Comme Shor, ils ont ensuite adapté l’algorithme pour résoudre une version réaliste du problème, en remplaçant les prédictions par de véritables équations mathématiques.

Les informaticiens tentent toujours de comprendre et de résoudre ce problème. Vaikuntanathan a comparé cela à une situation différente qui se produit lors de la compression de données : lorsque les informations sont compressées, deux bits peuvent accidentellement se glisser au même endroit, les écrasant ainsi. Les problèmes liés à l’anticipation de ces collisions afin de les éviter présentent certaines similitudes. "Il s'agit d'une classe de problèmes qui ressemblent essentiellement à ceci", a-t-il déclaré. "Peut-être que ces problèmes peuvent être résolus de manière quantique." résolus, fournissant un moyen de les tester. L’idée était que les problèmes non structurés pourraient nécessiter moins de ressources pour être programmés ou être moins sensibles au bruit car ils sont déjà stochastiques. Mais jusqu’à présent, ce nouveau problème semble encore trop avancé pour être résolu par les ordinateurs quantiques existants. "C'est un problème étrange. Je n'ai pas pensé à le définir", a déclaré Aaronson, "mais rétrospectivement, il présente des fonctionnalités très intéressantes." Exemples d'avantages quantiques significatifs sur les problèmes basés sur NP. De nombreux autres problèmes du monde quantique passeront-ils de presque insolubles à résolubles ? Il y a désormais encore plus de raisons de le penser. "Cela change dans une certaine mesure notre vision des problèmes que les ordinateurs quantiques sont capables de résoudre", a déclaré O'Donnell.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!