Maison >Périphériques technologiques >IA >Machine de Turing : Comment peut-on parler d'informatique en l'absence d'ordinateurs ?
Machine de Turing : Comment peut-on parler d'informatique en l'absence d'ordinateurs ?
- PHPzavant
- 2023-04-16 14:34:031583parcourir
En octobre 1950, un article intitulé « Can Machines Think » a été publié. Cet article propose un test horrible, dans lequel le testeur et le sujet (une personne réelle et une machine) sont séparés l'un de l'autre, et le sujet se voit poser des questions aléatoires via un appareil de communication et est demandé aux testeurs de deviner si la personne à qui ils parlaient c'était une personne réelle ou une machine.
Après plusieurs tests, si la machine peut amener chaque participant à faire plus de 30 % d'erreurs de jugement en moyenne, alors la machine a réussi le test et est considérée comme dotée d'une intelligence humaine.
C’est à ce moment-là que les gens ont réalisé pour la première fois que les robots pouvaient avoir une intelligence humaine. Ce test est le test de Turing dont parlent des millions de passionnés de science-fiction. Cet article a également valu à l'auteur Alan Turing le titre de « Père de l'intelligence artificielle ».
La route vers l'intelligence artificielle, ou l'origine de l'histoire du développement informatique, est un article publié par Turing quand il avait 24 ans. Dans cet article, il donne une définition mathématique stricte de la « calculabilité » et propose l'idée de la célèbre « Machine de Turing ». La machine de Turing n'est pas une machine spécifique, mais un modèle mental capable de créer un dispositif informatique très simple mais extrêmement puissant pouvant être utilisé pour calculer toutes les fonctions calculables imaginables.
Parce que Turing a inventé la machine de Turing, de temps en temps, quelqu'un saute et prétend que Turing a en fait "inventé l'ordinateur". Cependant, les machines de Turing ne sont pas conçues de la même manière que les machines informatiques réelles. Une machine de Turing n’est même pas un modèle abstrait de machine. Il s'avère (comme en témoignent les remarques de Turing) qu'une machine de Turing est le modèle d'une personne écrivant sur du papier sur une table. Alors, pourquoi Turing a-t-il inventé la machine de Turing, et où la machine de Turing nous mènera-t-elle ?
1 L'article de Turing "Sur les nombres calculables"
La meilleure façon de répondre à ces questions est de mettre le manuel de côté et d'ouvrir le papier. Aujourd'hui, pour emprunter un périodique de 1936, il n'est pas nécessaire de remplir une carte de prêt ou d'attendre une heure qu'un bibliothécaire vienne le chercher à la bibliothèque. Tout ce dont nous avons besoin, c'est d'un verre de whisky de malt à la main et d'un accès facile à Google à la maison. L'article de Turing que nous recherchons est le suivant :

Adresse du papier : https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf
Il y a quelques erreurs dans le papier, mais les défauts ne cachent pas les vertus. Comme l'a dit Joel David Hamkins, Turing a défini les nombres réels calculables comme des nombres avec des expansions décimales calculables, ce qui ne fonctionne pas en réalité, mais n'est pas difficile à corriger.
Turing a expliqué l'intention d'écrire cet article dans le titre : "Sur les nombres calculables et leur application dans les "problèmes de décision"". Le "Entscheidungsproblem (problème de décision)" demande s'il existe des techniques efficaces pour déterminer qu'un problème donné. La formule logique du premier ordre est valide, c'est-à-dire vraie dans toutes les interprétations
Turing a développé son idée comme suit :
Nous pouvons comparer une personne qui calcule des nombres réels à un ordinateur qui ne peut satisfaire qu'un nombre limité. nombre de conditions q1, q2,... qR.... Il y a une longue « bande de papier » qui passe à travers cette machine, et la bande de papier est divisée en plusieurs parties, une pièce à la fois, nous les appelons des carrés, et. chaque carré peut contenir un « symbole »... Certains des symboles écrits formeront la séquence décimale des nombres réels calculés, tandis que d'autres symboles ne sont que des « aides-mémoire ». Notes approximatives Ces notes approximatives peuvent être effacées. que cette opération consistant à glisser sur un morceau de papier et à faire quelque chose avec ce symbole inclut tout. Les opérations utilisées pour les calculs numériques
...
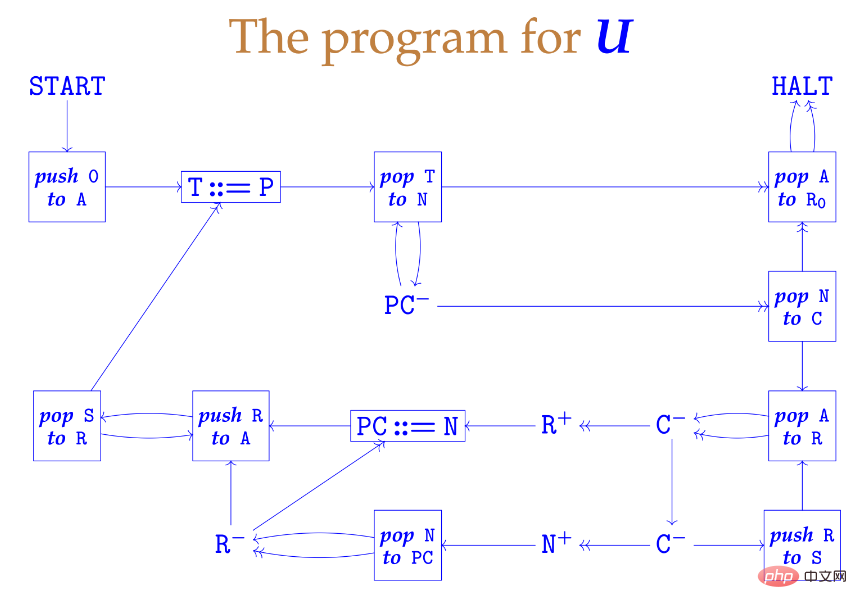
Un "nombre calculable" est simplement un nombre réel dont la représentation décimale. est calculable par des moyens limités. Selon ma définition, si un nombre a une forme décimale. Si l'expression peut être écrite par une machine, alors le nombre est calculable par la suite. Turing l'a défini et prouvé. ce n'est pas un article d'ingénierie typique. Dans ce type d'article, les lecteurs aimeraient voir une discussion sur la façon de mettre en œuvre certains des mécanismes décrits dans l'article. Comme nous pouvons le voir dans le titre et l'article de Turing, Turing s'intéresse principalement aux calculs réels. nombres à des décimales infinies. Cet article a de nombreuses autres contributions importantes : Après avoir rédigé cet article, Turing a ouvert la porte au domaine de l'informatique théorique. Maintenant, nous disposons d'une machine de Turing universelle qui a été conçue de manière incisive et vivante. Il y a plusieurs décennies, à l'Université de Cambridge, le Dr Ken Moody a écrit un keygen universel Minsky :
Lien : http://www.igblan.free-online.co.uk/igblan/ca/minsky. html Une telle machine possède un nombre limité de registres, chacun pouvant stocker un entier non négatif arbitrairement grand. Il a un programme fini composé de trois types différents d'instructions étiquetées : Incrémenter le registre Moody utilise une bijection standard entre N et pour regrouper une liste d'entiers en un seul entier. Il a écrit une petite bibliothèque de petites machines de registre qui effectuaient des opérations telles que pousser et retirer la pile, et a créé une conception qui rappelait le cycle d'exécution de récupération d'un vrai processeur. L'ensemble du processus peut être vu dans les diapositives suivantes. L'image ci-dessous est la machine elle-même : Étonnamment, la structure de cette machine est si simple ! 3 Le problème de l'arrêt Maurice Wilkes : Je pense qu'un ingénieur considérerait l'idée de programmes stockés comme une théorie importante similaire à la Trinité, et dirait : « C'est absolument de première classe, et cela devrait être fait de cette façon. " Il n'y a aucune différence pratique entre les idées contenues dans cet article et ce que j'ai dit. Il a eu de la chance de faire publier cet article, je veux dire qu'Alonzo Church a obtenu le même résultat en utilisant d'autres méthodes. Adresse de l'article : https://cacm.acm.org/magazines/2009/9/38898-an-interview-with-maurice-wilkes/fulltext
Il est à noter que , Au moment de l'interview, Maurice Wilkes avait 96 ans. Il était un célèbre pionnier de l'informatique et le père de l'EDSAC (Electronic Delay Storage Automatic Calculator). Dans son étrange réponse, on peut voir sa jalousie à l’égard du statut élevé de Turing. Ces deux-là ne s'entendent visiblement pas ! Nous voyons également le dédain de Maurice Wilkes pour la théorie : même si le codage de la machine en nombres était attendu d'un ordinateur à programme stocké, le travail de Turing était de pures mathématiques et n'avait aucune signification technique. Turing s'intéressait à l'ingénierie informatique proprement dite, mais ses nombreuses tentatives de participation à des projets réels ont été vaines. Et comment évaluez-vous ces remarques sur Church ? Turing et Church étaient à Princeton
Honnêtement, ce document est difficile à lire, mais il peut nous y emmener Soyez présent la situation. Cet article donne une définition du λ-calcul, une définition d'une fonction récursive (au sens de Kleene/Gödel), et quelques questions incontestables sur l'existence et l'équivalence des paradigmes dans le résultat du jugement. Church et Craney avaient prouvé l'équivalence entre les fonctions définissables par lambda et les fonctions récursives ; et pendant que Turing était à Princeton, l'équivalence entre les fonctions définissables par lambda et les fonctions calculables par Turing avait également été prouvée, nous obtenons donc la thèse de Church-Turing, qui fait référence au fait que les fonctions effectivement calculables sont précisément les fonctions de la classe d'équivalence mathématique. 6 La thèse Church-Turing est-elle correcte ? La forme moderne de la fonction Ackermann est la suivante : Lien de l'article : https://lawrencecpaulson.github.io/2022/02/09/Ackermann-example.html Si vous définissez f(n)=A(n,n), nous ne pouvons pas nous attendre à calculer un nombre pair f(4). g(n)=A(4,n), bien que récursif primitif, est presque impossible à calculer. Bien qu'il n'y ait pas d'ordinateurs numériques avant les années 1930, le concept de calculabilité efficace était bien connu des mathématiciens. Le concept de validité est apparu depuis longtemps dans la structure en ligne droite et en boussole de la géométrie grecque. La validité fait également partie intégrante du problème de décision et du dixième problème de Hilbert. Le génie du concept de Turing, comparé aux fonctions récursives de Gödel et au lambda calcul de Church, est qu'il est évidemment correct. Gödel lui-même n'était pas sûr que sa fonction récursive capturait l'idée de calcul, et nous ne savons pas si l'idée de Church était correcte. Seules les idées de Turing étaient simples et naturelles. Les idées de Turing sont manifestement équivalentes à d’autres modèles et fournissent des explications raisonnables pour chacun d’entre eux. Il a souligné ce fait dans son article de 1937 « Computability and Lambda-Definability ». Cet article vise à prouver que la fonction calculable proposée par l'auteur et la λ-fonction définissable de Church ainsi que la fonction récursive générale proposée par Elbron et Gödel et développée par Klenny sont les mêmes. Ces mêmes fonctions prouvent que chaque fonction définie par X est calculable et que chaque fonction calculable est généralement récursive. Notez que Turing a écrit "calculable", mais nous devons écrire "Turing calculable".
2 Puisque le but d'une machine de Turing est de simuler un employé travaillant à un bureau, et que le fonctionnement d'une machine de Turing est le même que celui d'un employé : effectuer telle ou telle opération selon une liste donnée de règles de transformation basées sur la machine. symboles d'état et de bande - il est évidemment nécessaire une machine de Turing pour effectuer de telles tâches de routine. L'article de Turing était un peu sommaire sur les détails de la construction, mais personne ne semblait s'en soucier.


Le problème du décrochage est évidemment indécidable. Sinon, de nombreuses conjectures mathématiques seront difficiles à résoudre, comme le dernier théorème de Fermat : écrivez simplement un programme qui recherche x, y, z, n>2, tel que
, et demandez s'il se termine. Mais l’indécidabilité de l’arrêt doit être rigoureusement exprimée et prouvée. 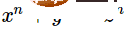 Contrairement à la croyance populaire, l'article de Turing ne discute pas du problème de l'arrêt, mais discute d'une caractéristique liée au problème de l'arrêt, qu'il appelle « circularité ». Une machine de Turing est cyclique si elle « n'écrit qu'un nombre limité de premiers symboles » (c'est-à-dire des 0 et des 1). Je pense que la raison pour laquelle la cyclicité est importante est que Turing aimait particulièrement approximer les nombres réels sous forme de chaînes binaires infinies. Le physicien Christopher Strachey a affirmé dans une lettre de 1965 au Computer Journal que Turing lui avait fourni une preuve de l'indécidabilité du problème d'arrêt.
Contrairement à la croyance populaire, l'article de Turing ne discute pas du problème de l'arrêt, mais discute d'une caractéristique liée au problème de l'arrêt, qu'il appelle « circularité ». Une machine de Turing est cyclique si elle « n'écrit qu'un nombre limité de premiers symboles » (c'est-à-dire des 0 et des 1). Je pense que la raison pour laquelle la cyclicité est importante est que Turing aimait particulièrement approximer les nombres réels sous forme de chaînes binaires infinies. Le physicien Christopher Strachey a affirmé dans une lettre de 1965 au Computer Journal que Turing lui avait fourni une preuve de l'indécidabilité du problème d'arrêt. 4 Quelle est l'importance de l'article de Turing de 1936 sur le problème de la décision ?
Lien du papier : https://www.jstor.org/stable/2371045?origin=crossref

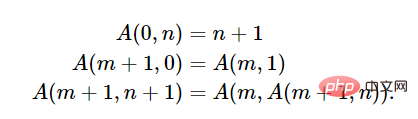
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

