Le nombre d’articles a fortement augmenté au cours des dix dernières années. Comment l’apprentissage profond ouvre-t-il lentement la porte au raisonnement mathématique ?

Le raisonnement mathématique est une manifestation clé de l'intelligence humaine, nous permettant de comprendre et de prendre des décisions basées sur des données numériques et le langage. Le raisonnement mathématique s'applique à une variété de domaines, notamment les sciences, l'ingénierie, la finance et la vie quotidienne, et englobe une gamme de capacités allant des compétences de base telles que la reconnaissance des formes et la calcul des nombres aux compétences avancées telles que la résolution de problèmes, le raisonnement logique et la pensée abstraite.

Depuis longtemps, le développement de systèmes d'IA capables de résoudre des problèmes mathématiques et de prouver des théorèmes mathématiques est un axe de recherche dans les domaines de l'apprentissage automatique et du traitement du langage naturel. Cela remonte également aux années 1960.

Au cours des dix dernières années depuis l'essor du deep learning, l'intérêt des gens pour ce domaine a considérablement augmenté :

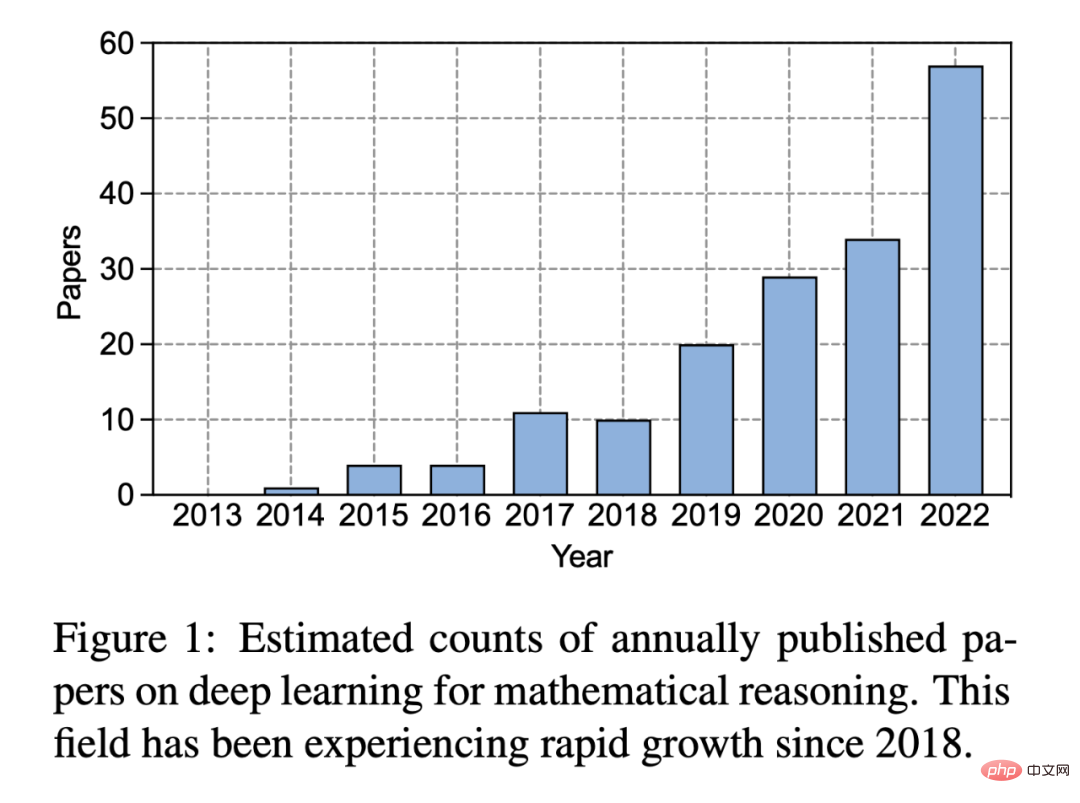
Figure 1 : Nombre estimé d'articles sur le deep learning sur le raisonnement mathématique publiés chaque année . Depuis 2018, ce domaine connaît une croissance rapide.

Le deep learning a connu un grand succès dans diverses tâches de traitement du langage naturel, telles que la réponse aux questions et la traduction automatique. De même, les chercheurs ont développé diverses méthodes de réseaux neuronaux pour le raisonnement mathématique, qui se sont révélées efficaces dans la gestion de tâches complexes telles que les problèmes de mots, la démonstration de théorèmes et la résolution de problèmes géométriques. Par exemple, les résolveurs de problèmes d’application basés sur l’apprentissage profond adoptent un cadre séquence à séquence et utilisent un mécanisme d’attention comme étape intermédiaire pour générer des expressions mathématiques. De plus, avec des corpus à grande échelle et des modèles Transformer, les modèles de langage pré-entraînés ont obtenu des résultats prometteurs sur diverses tâches mathématiques. Récemment, de grands modèles de langage comme GPT-3 ont fait progresser le domaine du raisonnement mathématique en démontrant des capacités impressionnantes en matière de raisonnement complexe et d'apprentissage contextuel.

Dans un rapport récemment publié, des chercheurs de l'UCLA et d'autres institutions ont systématiquement examiné les progrès de l'apprentissage profond dans le raisonnement mathématique.

Lien papier : https://arxiv.org/pdf/2212.10535.pdf

Adresse du projet : https://github.com/lupantech/dl4math

Spécifique En particulier, cet article discute de diverses tâches et ensembles de données (Section 2) et examine les progrès des réseaux de neurones (Section 3) et des modèles de langage pré-entraînés (Section 4) dans le domaine des mathématiques. Le développement rapide de l'apprentissage contextuel de grands modèles de langage dans le raisonnement mathématique est également exploré (Section 5). L'article analyse plus en détail les références existantes et constate que moins d'attention est accordée aux environnements multimodaux et à faibles ressources (Section 6.1). Des recherches fondées sur des données probantes montrent que les représentations actuelles des capacités informatiques sont inadéquates et que les méthodes d’apprentissage profond sont incohérentes en ce qui concerne le raisonnement mathématique (section 6.2). Par la suite, les auteurs suggèrent des améliorations aux travaux actuels en termes de généralisation et de robustesse, de raisonnement fiable, d’apprentissage à partir du feedback et de raisonnement mathématique multimodal (Section 7).

Tâches et ensembles de données

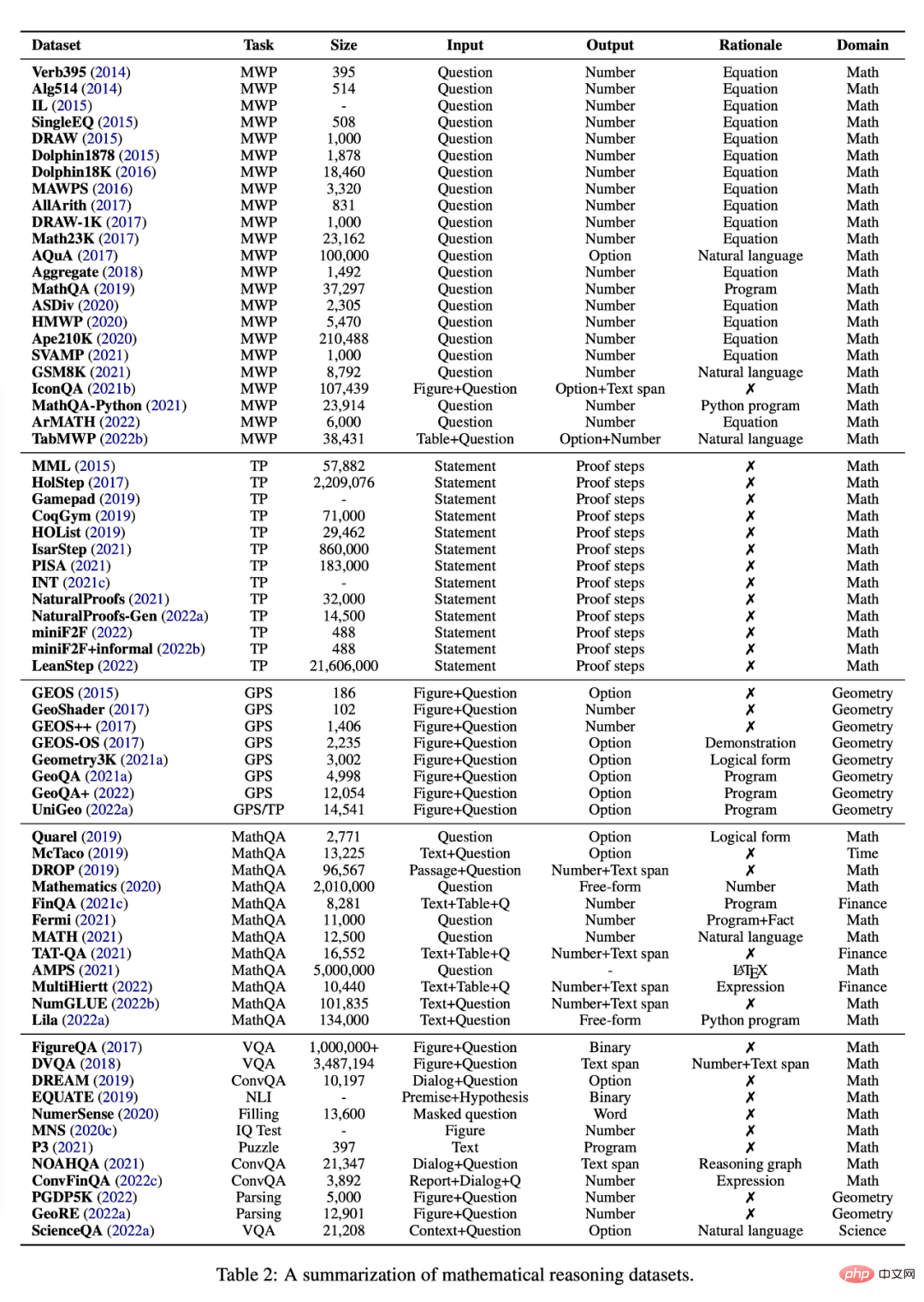
Cette section examine les différentes tâches et ensembles de données actuellement disponibles pour étudier le raisonnement mathématique à l'aide de méthodes d'apprentissage profond, voir le tableau 2.

Problème de mots (Problème de mots mathématiques)

Un problème de mots contient une brève description impliquant des personnes, des entités et des quantités. La relation mathématique peut être modélisée par un ensemble d'équations. L'équation révèle la réponse finale à la question. Le tableau 1 est un exemple typique. Une question implique les quatre opérations mathématiques de base que sont l'addition, la soustraction, la multiplication et la division, avec des étapes simples ou multiples. Le défi des problèmes d’application aux systèmes PNL réside dans la demande de compréhension du langage, d’analyse sémantique et de diverses capacités de raisonnement mathématique.

Les ensembles de données existants sur les problèmes de mots couvrent des questions de niveau primaire qui sont extraites de sites Web d'apprentissage en ligne, collectées à partir de manuels scolaires ou annotées manuellement par des humains. Les premiers ensembles de données sur les problèmes de mots étaient relativement petits ou limités à un petit nombre d'étapes. Certains ensembles de données récents visent à accroître la variété et la difficulté du problème. Par exemple, Ape210K, le plus grand ensemble de problèmes publics actuel, comprend 210 000 problèmes de mots pour les écoles élémentaires, tandis que les problèmes de GSM8K peuvent impliquer jusqu'à 8 solutions ; SVAMP est une référence qui teste la robustesse des modèles d'apprentissage profond pour formuler des problèmes avec des variations simples. Certains ensembles de données récemment établis impliquent également des modalités autres que le texte. Par exemple, IconQA fournit un diagramme abstrait comme arrière-plan visuel, tandis que TabMWP fournit un arrière-plan tabulaire pour chaque question.

La plupart des ensembles de données de problèmes de mots fournissent des raisons pour annoter les équations comme solutions (voir tableau 1). Pour améliorer les performances et l'interprétabilité des solveurs appris, MathQA est annoté avec des procédures de calcul précises, et MathQA-Python fournit des procédures Python concrètes. D’autres ensembles de données annotent les questions avec des solutions en langage naturel en plusieurs étapes considérées comme plus adaptées à la lecture humaine. Lila a annoté de nombreux ensembles de données de problèmes de mots mentionnés précédemment en utilisant les principes de programmation Python.

Preuve théorique

L'automatisation de la preuve de théorèmes est un défi à long terme dans le domaine de l'IA. Le problème consiste généralement à prouver la vérité d’un théorème mathématique à l’aide d’une série d’arguments logiques. La démonstration de théorèmes implique diverses compétences, telles que le choix de stratégies efficaces en plusieurs étapes, l'utilisation de connaissances de base et l'exécution d'opérations symboliques telles que l'arithmétique ou les dérivations.

Récemment, l'utilisation de modèles de langage pour la preuve de théorèmes dans des démonstrateurs de théorèmes interactifs formels (ITP) a suscité un intérêt croissant. Un théorème est énoncé dans le langage de programmation d'ITP puis simplifié en générant des « étapes de preuve » jusqu'à ce qu'il soit réduit à un fait connu. Le résultat est une séquence d’étapes qui constituent une preuve vérifiée.

La preuve informelle de théorèmes propose un moyen alternatif pour la preuve de théorèmes, qui consiste à écrire des déclarations et des preuves dans une forme hybride de langage naturel et de notation mathématique « standard » (telle que LATEX) et à faire vérifier leur exactitude par des humains.

Un domaine de recherche émergent vise à combiner des éléments de preuve informelle et formelle de théorèmes. Par exemple, Wu et al. (2022b) explorent la traduction de déclarations informelles en déclarations formelles, tandis que Jiang et al. (2022b) ont publié une nouvelle version du benchmark miniF2F qui ajoute des déclarations et des preuves informelles, appelée miniF2F+informal. Jiang et al. (2022b) explorent la conversion de preuves informelles fournies (ou générées) en preuves formelles.

Problèmes géométriques

La résolution automatisée de problèmes géométriques (GPS) est également une tâche d'intelligence artificielle de longue date dans la recherche sur le raisonnement mathématique et a attiré une large attention ces dernières années. Contrairement aux problèmes de mots, les problèmes de géométrie consistent en des descriptions de textes en langage naturel et des figures géométriques. Comme le montre la figure 2, l'entrée multimodale décrit les entités, les propriétés et les relations des éléments géométriques, tandis que l'objectif est de trouver des solutions numériques à des variables inconnues. Le GPS est une tâche difficile pour les méthodes d’apprentissage profond en raison des compétences complexes requises. Cela implique la capacité d'analyser des informations multimodales, de s'engager dans l'abstraction symbolique, d'utiliser la connaissance des théorèmes et de s'engager dans un raisonnement quantitatif.

Les premiers ensembles de données ont favorisé la recherche dans ce domaine, mais ces ensembles de données sont relativement petits ou non accessibles au public, ce qui limite le développement de méthodes d'apprentissage profond. Pour remédier à cette limitation, Lu et al. Récemment, des ensembles de données à plus grande échelle tels que GeoQA, GeoQA+ et UniGeo ont été introduits et annotés avec des programmes qui peuvent être appris et exécutés par des solveurs neuronaux pour obtenir des réponses finales.

Questions et réponses sur les mathématiques

Des recherches récentes montrent que les systèmes de raisonnement mathématique SOTA peuvent être « fragiles » dans leur raisonnement, c'est-à-dire que le modèle s'appuie sur de faux signaux provenant d'ensembles de données spécifiques et de calculs plug-and-play pour obtenir des performances « satisfaisantes ». Afin de résoudre ce problème, de nouveaux benchmarks ont été proposés sous différents aspects. L'ensemble de données Mathematics (Saxton et al., 2020) comprend de nombreux types différents de problèmes mathématiques, couvrant l'arithmétique, l'algèbre, les probabilités et le calcul. Cet ensemble de données peut mesurer la capacité de généralisation algébrique du modèle. De même, MATH (Hendrycks et al., 2021) consiste à mettre au défi des mathématiques de compétition pour mesurer la capacité d'un modèle à résoudre des problèmes dans des situations complexes.

Certains travaux ont ajouté un arrière-plan de tableau à la saisie des questions. Par exemple, FinQA, TAT-QA et MultiHiertt collectent des questions qui nécessitent une compréhension des tableaux et un raisonnement numérique pour y répondre. Certaines études ont proposé des critères unifiés pour le raisonnement numérique à grande échelle. NumGLUE (Mishra et al., 2022b) est un benchmark multitâche qui vise à évaluer les performances du modèle sur huit tâches différentes. Mishra et al. 2022a ont approfondi cette direction en proposant Lila, qui se compose de 23 tâches de raisonnement numérique couvrant un large éventail de sujets mathématiques, de complexité du langage, de formats de questions et d'exigences de connaissances de base.

L'IA a également réussi dans d'autres types de problèmes quantitatifs. Les chiffres, les graphiques et les dessins, par exemple, sont des supports essentiels pour transmettre de grandes quantités d’informations de manière concise. FigureQA, DVQA, MNS, PGDP5K et GeoRE ont tous été introduits pour étudier la capacité des modèles à raisonner sur les relations quantitatives entre des entités basées sur des graphiques. NumerSense étudie si et dans quelle mesure les modèles linguistiques pré-entraînés existants sont capables de détecter les connaissances numériques de bon sens. EQUATE formalise divers aspects du raisonnement quantitatif dans un cadre de raisonnement en langage naturel. Le raisonnement quantitatif apparaît également fréquemment dans des domaines spécifiques tels que la finance, la science et la programmation. Par exemple, ConvFinQA effectue un raisonnement numérique sur des rapports financiers sous forme de questions et réponses conversationnelles ; ScienceQA implique un raisonnement numérique dans le domaine scientifique et P3 étudie la capacité de raisonnement fonctionnel des modèles d'apprentissage profond pour trouver une entrée valide pour un programme donné ; Vrai.

Réseaux de neurones pour le raisonnement mathématique

L'auteur de cet article a également résumé plusieurs réseaux de neurones courants utilisés pour le raisonnement mathématique.

Réseau Seq2Seq

Les réseaux neuronaux Seq2Seq ont été appliqués avec succès à des tâches de raisonnement mathématique telles que les problèmes de mots, la preuve de théorèmes, les problèmes de géométrie et la réponse à des questions mathématiques. Les modèles Seq2Seq utilisent une architecture codeur-décodeur qui formalise généralement le raisonnement mathématique comme une tâche de génération de séquence. L'idée de base de cette méthode est de mapper des séquences d'entrée (telles que des problèmes mathématiques) sur des séquences de sortie (telles que des équations, des programmes et des preuves). Les encodeurs et décodeurs courants incluent le réseau de mémoire à long terme (LSTM) et l'unité récurrente fermée (GRU). Des travaux approfondis ont montré que les modèles Seq2Seq présentent des avantages en termes de performances par rapport aux méthodes d'apprentissage statistique précédentes, y compris leurs variantes bidirectionnelles BiLSTM et BiGRU. DNS est le premier travail à utiliser le modèle Seq2Seq pour convertir des phrases de problèmes de mots en équations mathématiques.

Réseau basé sur des graphiques

La méthode Seq2Seq présente l'avantage de générer des expressions mathématiques et de ne pas s'appuyer sur des fonctionnalités créées à la main. Les expressions mathématiques peuvent être transformées en structures arborescentes, telles que des arbres de syntaxe abstraite (AST) et des structures basées sur des graphiques, qui décrivent les informations structurées contenues dans l'expression. Cependant, ces informations importantes ne sont pas explicitement modélisées par l’approche Seq2Seq. Pour résoudre ce problème, les chercheurs ont développé des réseaux de neurones basés sur des graphes pour modéliser explicitement la structure des expressions. Le modèle Sequence-to-tree (Seq2Tree) modélise explicitement la structure arborescente lors de l'encodage de la séquence de sortie. Par exemple, Liu et al. ont conçu un modèle Seq2Tree pour mieux utiliser les informations AST des équations. En revanche, Seq2DAG applique un cadre de graphe de séquence (Seq2Graph) lors de la génération d'équations, car le décodeur de graphe est capable d'extraire des relations complexes entre plusieurs variables. Les informations basées sur des graphiques peuvent également être intégrées lors du codage des séquences mathématiques d'entrée. Par exemple, ASTactic applique TreeLSTM sur AST pour représenter les objectifs d'entrée et les prémisses des preuves de théorèmes.

Réseau basé sur l'attention

​

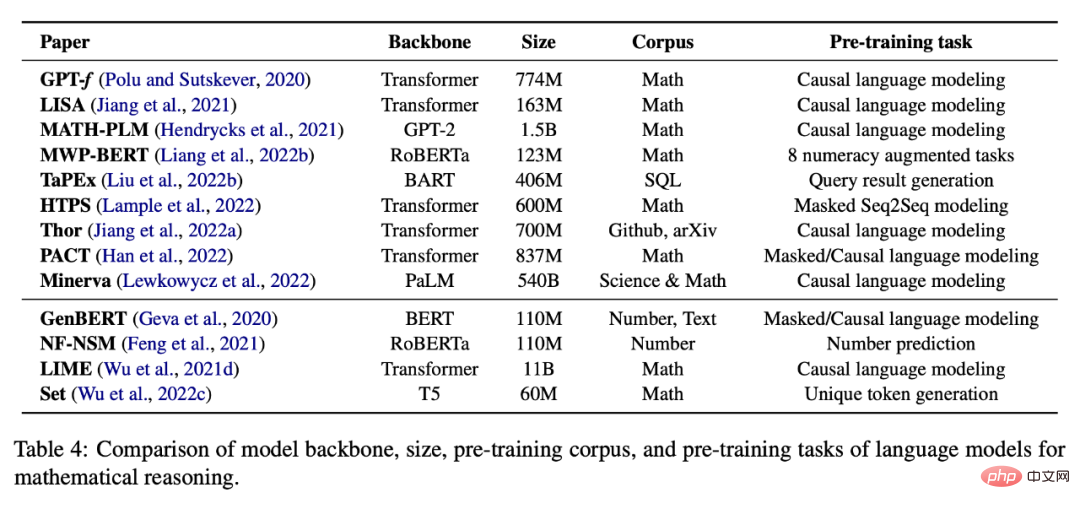
Le mécanisme d'attention a été appliqué avec succès aux problèmes de traitement du langage naturel et de vision par ordinateur, en tenant compte du vecteur caché d'entrée pendant le processus de décodage. Les chercheurs ont exploré son rôle dans les tâches de raisonnement mathématique, car il peut être utilisé pour identifier les relations les plus importantes entre les concepts mathématiques. Par exemple, MATH-EN est un outil de résolution de problèmes de mots qui bénéficie d'informations de dépendance à long terme apprises grâce à l'auto-attention. Les méthodes basées sur l'attention ont également été appliquées à d'autres tâches de raisonnement mathématique, telles que les problèmes de géométrie et la démonstration de théorèmes. Afin d'extraire de meilleures représentations, divers mécanismes d'attention ont été étudiés, tels que Group-ATT, qui utilise différentes attentions multi-têtes pour extraire divers types de fonctionnalités MWP, et l'attention graphique, qui est appliquée pour extraire des informations conscientes des connaissances.

Autres réseaux de neurones

Les méthodes d'apprentissage en profondeur pour les tâches de raisonnement mathématique peuvent également utiliser d'autres réseaux de neurones, tels que les réseaux de neurones convolutifs et les réseaux multimodaux. Certaines œuvres utilisent des architectures de réseaux neuronaux convolutifs pour coder le texte d'entrée, donnant au modèle la capacité de capturer les relations à long terme entre les symboles dans l'entrée. Par exemple, Irving et al. ont proposé la première application des réseaux de neurones profonds dans la démonstration de théorèmes, qui reposaient sur des réseaux convolutifs pour la sélection de prémisses dans les grandes théories.

Les tâches de raisonnement mathématique multimodal, telles que la résolution de problèmes géométriques et le raisonnement mathématique basé sur des graphiques, sont formalisées sous forme de questions à réponse visuelle aux questions (VQA). Dans ce domaine, les entrées visuelles sont codées à l'aide de ResNet ou Faster-RCNN, tandis que les représentations textuelles sont obtenues via GRU ou LTSM. Par la suite, les représentations conjointes sont apprises à l'aide de modèles de fusion multimodaux tels que BAN, FiLM et DAFA.

D'autres structures de réseaux neuronaux profonds peuvent également être utilisées pour le raisonnement mathématique. Zhang et al. ont exploité le succès des réseaux de neurones graphiques (GNN) dans le raisonnement spatial et l'ont appliqué à des problèmes géométriques. WaveNet est appliqué à la preuve de théorèmes en raison de sa capacité à résoudre des données de séries chronologiques longitudinales. De plus, il a été constaté que Transformer surpassait GRU dans la génération d'équations mathématiques en DDT. Et MathDQN est le premier travail explorant l’apprentissage par renforcement pour résoudre des problèmes de mots mathématiques, en tirant principalement parti de ses puissantes capacités de recherche.

Modèles linguistiques pré-entraînés pour le raisonnement mathématique

Les modèles linguistiques pré-entraînés ont montré des améliorations significatives des performances sur un large éventail de tâches de PNL et sont également appliqués à des problèmes liés aux mathématiques. modèles Le modèle fonctionne bien dans la résolution de problèmes de mots et aide à la preuve de théorèmes et à d'autres tâches mathématiques. Cependant, son utilisation à des fins de raisonnement mathématique présente plusieurs défis.

Tout d'abord, le modèle de langage pré-entraîné n'est pas spécifiquement entraîné sur des données mathématiques. Cela peut se traduire par une moindre maîtrise des tâches liées aux mathématiques par rapport aux tâches en langage naturel. Il y a également moins de données mathématiques ou scientifiques disponibles pour une pré-formation à grande échelle que les données textuelles.

Deuxièmement, la taille des modèles pré-entraînés continue de croître, ce qui rend coûteux la formation d'un modèle entier à partir de zéro pour une tâche spécifique en aval.

De plus, les tâches en aval peuvent gérer différents formats ou modalités d'entrée, tels que des tableaux ou des graphiques structurés. Pour relever ces défis, les chercheurs doivent affiner les modèles pré-entraînés ou ajuster les architectures neuronales sur les tâches en aval.

Enfin, bien que les modèles linguistiques pré-entraînés puissent coder une grande quantité d'informations linguistiques, à partir du seul objectif de la modélisation linguistique, il peut être difficile pour le modèle d'acquérir une représentation numérique ou des compétences de raisonnement de haut niveau. Dans cette optique, des recherches récentes ont étudié l’intégration de compétences liées aux mathématiques dans des cours commençant par les bases.

Apprentissage auto-supervisé des mathématiques

Le tableau 4 ci-dessous fournit une liste de modèles de langage pré-entraînés pour des tâches auto-supervisées de raisonnement mathématique. Le réglage fin spécifique à une tâche est également une pratique courante lorsqu'il n'y a pas suffisamment de données pour entraîner un grand modèle à partir de zéro. Comme le montre le tableau 5, les travaux existants tentent d'affiner les modèles de langage pré-entraînés sur diverses tâches en aval.

En plus d'affiner les paramètres du modèle, de nombreux travaux utilisent également des modèles de langage pré-entraînés comme encodeurs et les combinent avec d'autres modules pour effectuer des tâches en aval. Par exemple, IconQA propose d'utiliser ResNet et BERT respectivement pour la reconnaissance de graphiques et la compréhension de texte. .

Apprentissage contextuel dans le raisonnement mathématique

Un échantillon d'un contexte contient généralement une paire entrée-sortie et quelques mots d'invite, par exemple, veuillez sélectionner le plus grand nombre dans la liste.

Entrée : [2, 4, 1, 5, 8]

Sortie : 8.

L'apprentissage en quelques coups donnera plusieurs échantillons, puis le modèle prédit la sortie sur le dernier échantillon d'entrée. Cependant, cette invite standard en quelques étapes, qui fournit de grands modèles de langage avec des échantillons contextuels de paires entrée-sortie avant les échantillons au moment du test, ne s'est pas avérée suffisante pour obtenir de bonnes performances sur des tâches difficiles telles que le raisonnement mathématique.

L'invite de chaîne de pensée (CoT) utilise l'explication intermédiaire en langage naturel comme invite, permettant au grand modèle de langage de générer d'abord une chaîne de raisonnement, puis de prédire la réponse à une question d'entrée. Par exemple, une invite CoT pour résoudre des problèmes d'application peut être

Kojima et al. (2022) ont proposé de fournir au modèle l'invite « Réfléchissons étape par étape ! » raisonneurs. En dehors de cela, les travaux les plus récents se sont concentrés sur la manière d’améliorer le raisonnement en chaîne de pensée dans le cadre de l’inférence zéro. Ce type de travail est principalement divisé en deux parties : (i) sélectionner de meilleurs échantillons contextuels et (ii) créer de meilleures chaînes d'inférence.

Sélection d'échantillons contextuels

Les premiers travaux de chaîne de pensée consistaient à sélectionner des échantillons contextuels de manière aléatoire ou heuristique. Des recherches récentes ont montré que ce type d’apprentissage en quelques étapes peut être très instable selon différentes sélections d’exemples contextuels. Par conséquent, la question de savoir quels échantillons de raisonnement contextuel peuvent produire les invites les plus efficaces reste une question inconnue dans les cercles universitaires.

Pour remédier à cette limitation, certains travaux récents ont étudié diverses méthodes pour optimiser le processus de sélection d'échantillons de contexte. Par exemple, Rubin et al. (2022) ont tenté de résoudre ce problème en récupérant des échantillons sémantiquement similaires. Cependant, cette approche ne fonctionne pas bien sur les problèmes de raisonnement mathématique et il est difficile de mesurer la similarité si des informations structurées (telles que des tableaux) sont incluses. De plus, Fu et al. (2022) ont proposé une invite basée sur la complexité, sélectionnant des échantillons avec des chaînes de raisonnement complexes (c'est-à-dire des chaînes avec plus d'étapes de raisonnement) comme invites. Lu et al. (2022b) ont proposé une méthode pour sélectionner des échantillons contextuels par apprentissage par renforcement. Plus précisément, l'agent apprend à trouver le meilleur échantillon contextuel parmi un pool de candidats, dans le but de maximiser la récompense prévue pour un échantillon de formation donné lors de l'interaction avec l'environnement GPT-3. De plus, Zhang et al. (2022b) ont découvert que la diversification des exemples de problèmes peut également améliorer les performances du modèle. Ils ont proposé une approche en deux étapes pour construire des exemples de problèmes dans leur contexte : premièrement, diviser les problèmes d'un ensemble de données donné en plusieurs groupes, deuxièmement, sélectionner un problème représentatif dans chaque groupe et utiliser une chaîne de réflexion heuristique simple pour générer sa chaîne de raisonnement ; .

Chaîne de raisonnement de haute qualité​

Les premiers travaux sur la chaîne de réflexion reposaient principalement sur une seule chaîne de raisonnement annotée par l'homme comme invite. Cependant, la création manuelle de chaînes de raisonnement présente deux inconvénients : premièrement, à mesure que les tâches deviennent de plus en plus complexes, les modèles actuels peuvent ne pas être suffisants pour apprendre à effectuer toutes les étapes de raisonnement nécessaires et ne peuvent pas être facilement généralisés à différentes tâches, deuxièmement, un seul processus de décodage ; est facilement affecté par des étapes de raisonnement erronées, conduisant à des prédictions incorrectes dans la réponse finale. Pour remédier à cette limitation, les recherches récentes se sont principalement concentrées sur deux aspects : (i) la création manuelle d’exemples plus complexes, connus sous le nom de méthodes basées sur les processus ; (ii) l’utilisation de méthodes de type ensemble, connues sous le nom de méthodes basées sur les résultats ;

Après avoir évalué les références et les méthodes existantes, les auteurs discutent également des orientations futures de la recherche dans ce domaine. Pour plus de détails sur la recherche, veuillez vous référer à l’article original.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!