Traitement d'image Python : filtrage du domaine fréquentiel, réduction du bruit et amélioration de l'image

Le traitement d'images fait désormais partie intégrante de notre quotidien, impliquant divers domaines tels que les médias sociaux et l'imagerie médicale. Les images obtenues à partir d'appareils photo numériques ou d'autres sources telles que des photos satellites et des examens médicaux peuvent nécessiter un prétraitement pour supprimer ou améliorer le bruit. Le filtrage du domaine fréquentiel est une solution possible permettant de supprimer le bruit tout en améliorant la netteté de l’image.

La transformée de Fourier rapide (FFT) est une technique mathématique qui transforme les images du domaine spatial vers le domaine fréquentiel. C'est un outil clé pour la transformation de fréquence dans le traitement d'images. En utilisant une représentation dans le domaine fréquentiel d'une image, nous pouvons analyser efficacement l'image en fonction de son contenu fréquentiel, simplifiant ainsi l'application de procédures de filtrage pour éliminer le bruit. Cet article discutera des différentes étapes impliquées dans la transformation de fréquence d'une image de FFT en FFT inverse, combinée à l'utilisation du décalage FFT et du décalage FFT inverse.

Cet article utilise trois bibliothèques Python, à savoir openCV, Numpy et Matplotlib.

import cv2
 import numpy as np
 from matplotlib import pyplot as plt
 img = cv2.imread('sample.png',0) # Using 0 to read image in grayscale mode
 plt.imshow(img, cmap='gray')#cmap is used to specify imshow that the image is in greyscale
 plt.xticks([]), plt.yticks([])# remove tick marks
 plt.show()

1. La transformation de Fourier rapide (FFT)

La transformation de Fourier rapide (FFT) est une technique mathématique largement utilisée qui permet de convertir des images du domaine spatial au domaine fréquentiel. composant de base de la conversion de fréquence. Grâce à l'analyse FFT, la périodicité de l'image peut être obtenue et divisée en différentes composantes de fréquence pour générer un spectre d'image qui affiche l'amplitude et la phase de la composante de fréquence respective de chaque image.

f = np.fft.fft2(img)#the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f
 mag = 20*np.log(np.abs(f))
 plt.imshow(mag, cmap = 'gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.
 plt.title('Magnitude Spectrum')
 plt.xticks([]), plt.yticks([])
 plt.show()

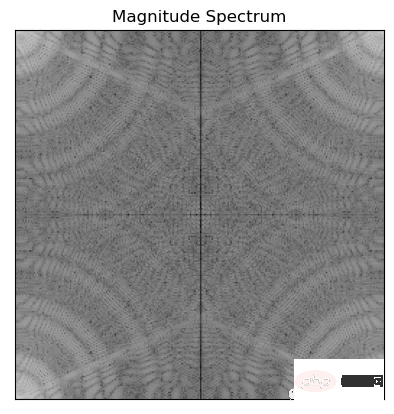
Le code ci-dessus calcule la magnitude de la transformée de Fourier f à l'aide de np.abs(), la convertit en une échelle logarithmique avec np.log(), puis la multiplie par 20 pour obtenir la magnitude en décibels. Ceci est fait pour rendre le spectre d’amplitude plus facile à visualiser et à interpréter.

2. Décalage FFT

Afin d'appliquer l'algorithme de filtrage à l'image, le décalage FFT est utilisé pour déplacer la composante de fréquence nulle de l'image vers le centre du spectre

fshift = np.fft.fftshift(f)
 mag = 20*np.log(np.abs(fshift))
 plt.imshow(mag, cmap = 'gray')
 plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])
 plt.show()

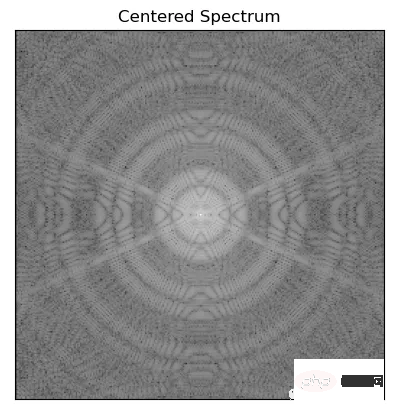
3. Filtrage

de transformation de fréquence L'un des objectifs est d'utiliser divers algorithmes de filtrage pour réduire le bruit et améliorer la qualité de l'image. Les deux filtres de netteté d’image les plus couramment utilisés sont le filtre passe-haut idéal et le filtre passe-haut gaussien. Ces filtres utilisent tous la représentation dans le domaine fréquentiel de l'image obtenue grâce à la méthode de transformée de Fourier rapide (FFT).

Le filtre passe-haut idéal est un filtre infiniment long avec une bande passante de fréquence infinie et des réponses idéales en bande passante et en bande d'arrêt. Les signaux de toutes les fréquences dans sa bande passante sont entièrement transmis, tandis que les signaux de toutes les fréquences dans sa bande d'arrêt sont complètement supprimés.

Dans le domaine fréquentiel, la réponse amplitude-fréquence d'un filtre idéal est :

• Dans la bande passante, la réponse amplitude-fréquence est de 1
• Dans la bande d'arrêt, la réponse amplitude-fréquence est de 0

Dans le domaine temporel, idéal La réponse impulsionnelle du filtre est :

• Dans la bande passante, la réponse impulsionnelle est une séquence de fonctions d'impulsion unitaire infiniment longue
• Dans la bande d'arrêt, la réponse impulsionnelle est nulle

Puisque le filtre idéal est à fréquence Il y a une bande passante illimitée sur le domaine, elle ne peut donc pas être mise en œuvre dans des applications pratiques. Les filtres numériques utilisés dans la pratique sont généralement basés sur une approximation du filtre idéal, ils ne constituent donc qu'un idéal.

Le filtre passe-haut gaussien est un filtre couramment utilisé dans le traitement d'images numériques. Sa fonction est de conserver les informations détaillées haute fréquence dans l'image et de supprimer les signaux basse fréquence. Ce filtre est basé sur une fonction gaussienne et possède une réponse en fréquence fluide qui peut s'adapter à une variété de détails de l'image.

La réponse en fréquence du filtre passe-haut gaussien peut être exprimée comme suit :

H(u,v) = 1 - L(u,v)

où L(u,v) est un filtre passe-bas , qui peut être utilisé pour la représentation de la fonction gaussienne. La réponse d'un filtre passe-haut est obtenue en soustrayant la réponse du filtre passe-bas de 1. En pratique, différents réglages de paramètres sont généralement utilisés pour ajuster la fonction gaussienne afin d'obtenir différents effets de filtrage.

Les images en forme de disque sont utilisées pour définir les composantes de fréquence à conserver ou à supprimer lorsque la transformation de Fourier est effectuée dans l'image. Dans ce contexte, un filtre idéal fait généralement référence à un filtre passe-bas ou passe-haut idéal qui peut être sélectionné dans le domaine fréquentiel pour conserver ou supprimer les signaux dans une plage de fréquences spécifique. Après avoir appliqué ce filtre idéal à la transformée de Fourier de l'image, puis effectué la transformation inverse, l'image traitée par le filtre peut être obtenue.

Nous n'entrerons pas dans les détails spécifiques, regardons directement le code :

La fonction suivante génère un masque circulaire pour des filtres passe-haut et passe-bas idéaux

import math
 def distance(point1,point2):
 return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
 
 def idealFilterLP(D0,imgShape):
 base = np.zeros(imgShape[:2])
 rows, cols = imgShape[:2]
 center = (rows/2,cols/2)
 for x in range(cols):
 for y in range(rows):
 if distance((y,x),center) < D0:
 base[y,x] = 1
 return base
 
 def idealFilterHP(D0,imgShape):
 base = np.ones(imgShape[:2])
 rows, cols = imgShape[:2]
 center = (rows/2,cols/2)
 for x in range(cols):
 for y in range(rows):
 if distance((y,x),center) < D0:
 base[y,x] = 0
 return base

La fonction suivante génère un filtre passe-haut gaussien filtre passe-bas et filtre passe-bas Exemple de filtre

import math
 def distance(point1,point2):
 return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
 
 def gaussianLP(D0,imgShape):
 base = np.zeros(imgShape[:2])
 rows, cols = imgShape[:2]
 center = (rows/2,cols/2)
 for x in range(cols):
 for y in range(rows):
 base[y,x] = math.exp(((-distance((y,x),center)**2)/(2*(D0**2))))
 return base
 
 def gaussianHP(D0,imgShape):
 base = np.zeros(imgShape[:2])
 rows, cols = imgShape[:2]
 center = (rows/2,cols/2)
 for x in range(cols):
 for y in range(rows):
 base[y,x] = 1 - math.exp(((-distance((y,x),center)**2)/(2*(D0**2))))
 return base

avec masque circulaire souhaité

fig, ax = plt.subplots(2, 2) # create a 2x2 grid of subplots
 fig.suptitle('Filters') # set the title for the entire figure
 
 # plot the first image in the top-left subplot
 im1 = ax[0, 0].imshow(np.abs(idealFilterLP(50, img.shape)), cmap='gray')
 ax[0, 0].set_title('Low Pass Filter of Diameter 50 px')
 ax[0, 0].set_xticks([])
 ax[0, 0].set_yticks([])
 
 # plot the second image in the top-right subplot
 im2 = ax[0, 1].imshow(np.abs(idealFilterHP(50, img.shape)), cmap='gray')
 ax[0, 1].set_title('High Pass Filter of Diameter 50 px')
 ax[0, 1].set_xticks([])
 ax[0, 1].set_yticks([])
 
 # plot the third image in the bottom-left subplot
 im3 = ax[1, 0].imshow(np.abs(gaussianLP(50 ,img.shape)), cmap='gray')
 ax[1, 0].set_title('Gaussian Filter of Diameter 50 px')
 ax[1, 0].set_xticks([])
 ax[1, 0].set_yticks([])
 
 # plot the fourth image in the bottom-right subplot
 im4 = ax[1, 1].imshow(np.abs(gaussianHP(50 ,img.shape)), cmap='gray')
 ax[1, 1].set_title('Gaussian Filter of Diameter 50 px')
 ax[1, 1].set_xticks([])
 ax[1, 1].set_yticks([])
 
 # adjust the spacing between subplots
 fig.subplots_adjust(wspace=0.5, hspace=0.5)
 
 # save the figure to a file
 fig.savefig('filters.png', bbox_inches='tight')

相乘过滤器和移位的图像得到过滤图像

为了获得具有所需频率响应的最终滤波图像，关键是在频域中对移位后的图像与滤波器进行逐点乘法。

这个过程将两个图像元素的对应像素相乘。例如，当应用低通滤波器时，我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。

此操作抑制高频并保留低频，对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的，从而产生更清晰和更清晰的图像。

它使我们能够获得期望的频率响应，并在频域获得最终滤波图像。

4、乘法滤波器（Multiplying Filter）和平移后的图像（Shifted Image）

乘法滤波器是一种以像素值为权重的滤波器，它通过将滤波器的权重与图像的像素值相乘，来获得滤波后的像素值。具体地，假设乘法滤波器的权重为h(i,j)，图像的像素值为f(m,n)，那么滤波后的像素值g(x,y)可以表示为：

g(x,y) = ∑∑ f(m,n)h(x-m,y-n)

其中，∑∑表示对所有的(m,n)进行求和。

平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率，但它们的像素位置发生了变化。在滤波操作中，平移后的图像可以用于与滤波器进行卷积运算，以实现滤波操作。

此操作抑制高频并保留低频，对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的，从而产生更清晰和更清晰的图像。

它使我们能够获得期望的频率响应，并在频域获得最终滤波图像。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(fftshifted_image * idealFilterLP(50,img.shape))), cmap='gray')
 ax.set_title('Filtered Image in Frequency Domain')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('filtered image in freq domain.png', bbox_inches='tight')

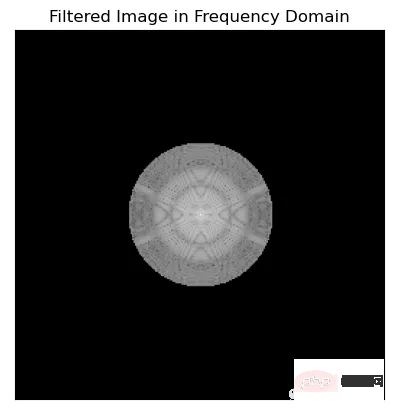
在可视化傅里叶频谱时，使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题，可以取决于具体的应用程序。

一般情况下会使用Np.log (1+np.abs(x))，因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的，并加上1以避免取零的对数。

而20*np.log(np.abs(x))将数据按20倍缩放，并对数据的绝对值取对数，这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。

这两种方法都有各自的优点和缺点，最终取决于具体的应用程序和个人偏好。

5、逆FFT位移

在频域滤波后，我们需要将图像移回原始位置，然后应用逆FFT。为了实现这一点，需要使用逆FFT移位，它反转了前面执行的移位过程。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape)))), cmap='gray')
 ax.set_title('Filtered Image inverse fft shifted')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')

6、快速傅里叶逆变换(IFFT)

快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比，图像减少了噪声并提高了清晰度。

fig, ax = plt.subplots()
 im = ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape))))), cmap='gray')
 ax.set_title('Final Filtered Image In Spatial Domain')
 ax.set_xticks([])
 ax.set_yticks([])
 
 fig.savefig('final filtered image.png', bbox_inches='tight')

总结

我们再把所有的操作串在一起显示，

函数绘制所有图像

def Freq_Trans(image, filter_used):
 img_in_freq_domain = np.fft.fft2(image)
 
 # Shift the zero-frequency component to the center of the frequency spectrum
 centered = np.fft.fftshift(img_in_freq_domain)
 
 # Multiply the filter with the centered spectrum
 filtered_image_in_freq_domain = centered * filter_used
 
 # Shift the zero-frequency component back to the top-left corner of the frequency spectrum
 inverse_fftshift_on_filtered_image = np.fft.ifftshift(filtered_image_in_freq_domain)
 
 # Apply the inverse Fourier transform to obtain the final filtered image
 final_filtered_image = np.fft.ifft2(inverse_fftshift_on_filtered_image)
 
 return img_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image

使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素，展示它们对增强图像清晰度的影响。

fig, axs = plt.subplots(12, 7, figsize=(30, 60))
 
 filters = [(f, d) for f in [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] for d in [50, 100, 150]]
 
 for row, (filter_name, filter_diameter) in enumerate(filters):
 # Plot each filter output on a separate subplot
 result = Freq_Trans(img, filter_name(filter_diameter, img.shape))
 
 for col, title, img_array in zip(range(7),
["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",
 f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],
[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])),
np.log(1+np.abs(result[4])), np.abs(result[5])]):
 
 axs[row, col].imshow(img_array, cmap='gray')
 axs[row, col].set_title(title)
 
 plt.tight_layout()
 plt.savefig('all_processess.png', bbox_inches='tight')
 plt.show()

Vous pouvez voir que lors de la modification du diamètre du masque circulaire, l'impact sur la clarté de l'image sera différent. À mesure que le diamètre augmente, davantage de fréquences sont supprimées, ce qui donne des images plus fluides et moins détaillées. La réduction du diamètre permet à davantage de fréquences de passer, ce qui donne des images plus nettes et plus détaillées. Afin d'obtenir l'effet souhaité, il est important de choisir le bon diamètre, car un diamètre trop petit donnera un filtre pas assez efficace, tandis qu'un diamètre trop grand donnera trop de détails. être perdu.

De manière générale, le filtre gaussien est plus couramment utilisé dans les tâches de traitement d'image en raison de sa finesse et de sa robustesse. Dans certaines applications, où une coupure plus nette est requise, un filtre idéal peut être plus adapté.

L'utilisation de FFT pour modifier la fréquence de l'image est une méthode efficace pour réduire le bruit et améliorer la netteté de l'image. Cela implique l'utilisation d'une FFT pour convertir l'image dans le domaine fréquentiel, l'utilisation de techniques appropriées pour filtrer le bruit et l'utilisation d'une FFT inverse pour reconvertir l'image modifiée dans le domaine spatial. En comprenant et en mettant en œuvre ces techniques, nous pouvons améliorer la qualité des images pour diverses applications.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!