Créez vos propres événements interactifs - reconnaissance des gestes sur écran

Cet article est un article d'un membre de l'équipe Front-end Byte Education-Adult and Innovation et a été autorisé par ELab à être publié.

TLDR

Cet article utilise l'apprentissage automatique, la méthode de détermination de la similarité cosinus et d'autres méthodes pour concevoir et vérifier un schéma de reconnaissance des gestes de la souris, et tente d'étendre le schéma à l'espace tridimensionnel.

Contexte

Le contenu principal de la technologie des terminaux est de répondre directement à l'interaction de l'utilisateur. La logique de base est qu'il existe des événements d'interaction prédéfinis sous une plate-forme spécifique et que les actions d'interaction spécifiques de l'utilisateur déclencheront les événements d'interaction correspondants. Toute la conception de l’interaction utilisateur-produit est également basée sur cela. Afin d’obtenir une bonne expérience utilisateur, une interaction pratique est nécessaire.

Dans le scénario PC, la souris (trackpad) est le périphérique d'entrée le plus important en plus du clavier. Les opérations courantes de la souris sont les boutons et la molette de la souris, donc les événements d'interaction courants correspondants sont le clic, le défilement et le déplacement. et ces interactions nécessitent un objet (comme cliquer sur un bouton, faire défiler une zone de contenu ou la totalité de la fenêtre, faire glisser une image), ce qui n'est pas aussi pratique que les touches de raccourci. Cependant, dans certains scénarios, les touches de raccourci ne sont pas aussi pratiques que la souris, nous nous attendons donc à ce que la souris dispose également d'opérations de raccourci. Les gestes de la souris constituent une opération de raccourci relativement spécialisée, mais pratique et facile à utiliser. Les gestes courants de la souris incluent le dessin de lignes droites, le marquage et le dessin de cercles. Au début, lorsque les navigateurs étaient florissants, de nombreux navigateurs nationaux utilisaient les opérations gestuelles pratiques de la souris comme argument de vente majeur afin de différencier leurs avantages concurrentiels. À cette époque, les opérations gestuelles ont progressivement gagné en soutien et en application, cultivant tranquillement le marché et les utilisateurs. habitudes.

Dans les scénarios d'écran tactile mobile, les avantages des opérations gestuelles sont plus évidents. Les opérations gestuelles ont évolué vers le classique « glisser vers la gauche pour revenir en arrière », « glisser vers la droite pour avancer », « glisser vers le haut pour revenir à la page d'accueil ». " faites glisser votre doigt vers le bas pour actualiser/évoquer les notifications/ " Réveillez le centre de contrôle ".

Avec l'essor récent de la VR/AR/MR, les opérations gestuelles dans l'espace tridimensionnel ont été davantage promues et appliquées.

Par conséquent, nous prenons le côté PC comme exemple pour réaliser la reconnaissance des gestes de la souris, clarifier la logique de base de mise en œuvre des gestes interactifs et, par analogie, essayer d'étendre la solution à des scénarios plus terminaux.

Objectif

• Implémentation de la logique de base : réaliser l'enregistrement et la reconnaissance des gestes de la souris. Pour les gestes de la souris, nous stipulons quelques prérequis :

Le panoramique et le zoom ne seront pas déformés, c'est-à-dire que la position globale et la taille du chemin du geste ne sont pas importantes.

Il présente une certaine tolérance aux gestes répétés des utilisateurs.

• Encapsulation technique : solidifiez-la en un événement personnalisé, qui peut être surveillé via addEventListener, élargissant ainsi la diversité des interactions et améliorant la commodité du développement.
• Expérience produite : permettez aux utilisateurs d'ajouter leurs propres gestes personnalisés.
• Mise à niveau dimensionnelle de la solution : étendez la solution actuellement explorée à l'espace tridimensionnel.

Analyse du problème

La particularité de ce problème est la gestion de l'incertitude. Il y a une incertitude dans les gestes de la souris dessinés par l'utilisateur.

Pour le cas où un chemin standard est prédéfini, le problème se transforme en détection de la similitude entre le « chemin déterministe prédéfini » et le « chemin incertain saisi par l'utilisateur ».

Pour le cas de chemins définis par l'utilisateur, le problème se transforme en détection de similitude entre « le chemin d'incertitude défini par l'utilisateur » et « le chemin d'incertitude entré par l'utilisateur ».

Si vous suivez le modèle de programmation traditionnel, vous devez exiger une logique de programme rigoureuse, définir des règles claires pour les jugements conditionnels et mesurer avec précision cette incertitude. C'est-à-dire qu'une « opération magique » est nécessaire. En substituant les deux chemins, vous pouvez déterminer s'ils sont similaires.

Quant au geste lui-même, on peut le considérer comme une image raster ordinaire ou comme un graphique vectoriel. Pour les images raster, nous pouvons utiliser des méthodes classiques d’apprentissage automatique pour déterminer la classification de l’image sans avoir à comprendre le contenu de l’image. Pour les graphiques vectoriels, nous devons définir une structure de données spéciale et approfondir la représentation de la similitude des graphiques. Notre prochaine implémentation partira de ces deux idées.

Plan de mise en œuvre

​Utiliser l'apprentissage automatique​

Idée de base

Tout d'abord, vous devez changer votre façon de penser. La programmation par apprentissage automatique est complètement différente de la pensée programmatique traditionnelle. Comme mentionné tout à l'heure, la programmation traditionnelle exige que la logique du programme, telle que les jugements conditionnels, les boucles et autres processus, soit spécifiée avec précision et codée manuellement. La programmation d'apprentissage automatique ne se limite plus à la formulation et à l'écriture de règles logiques détaillées, mais construit des réseaux de neurones pour permettre à l'ordinateur d'apprendre des fonctionnalités.

La clé de l'apprentissage automatique est un ensemble de données volumineux et fiable. Ce travail d'étiquetage prend beaucoup de temps. Afin de vérifier la faisabilité, nous utilisons l'ensemble de données de chiffres manuscrites similaire pour remplacer la scène gestuelle réelle.

Donc, nos prochaines étapes sont :

• Choisissez un modèle d'apprentissage automatique approprié en fonction des caractéristiques du problème.
• Choisissez un framework d'apprentissage automatique basé sur la facilité d'utilisation.
• Formez le modèle et obtenez le fichier modèle.
• Déployez et exécutez le modèle et tirez des conclusions.

Sélection de modèles

Il existe de nombreux algorithmes et modèles pour l'apprentissage automatique, et ils doivent être sélectionnés pour différents domaines. Tensorflow.js fournit officiellement une série de modèles pré-entraînés [1], qui peuvent être utilisés directement ou recyclés et utilisés.

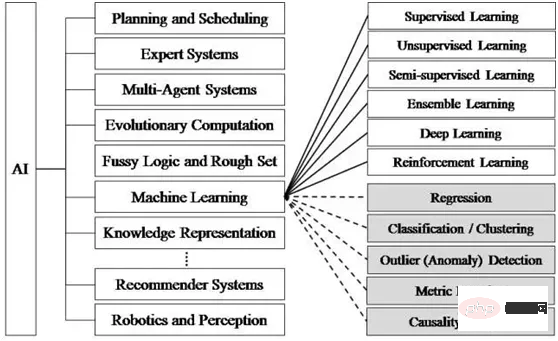
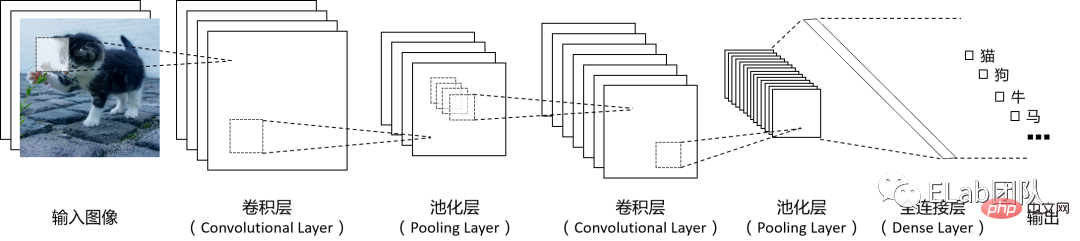
Les réseaux de neurones convolutionnels (CNN) sont un modèle d'apprentissage automatique très largement utilisé, notamment lors du traitement d'images ou d'autres données avec des caractéristiques raster, ils ont de très bonnes performances. Lors du traitement de l'information, CNN prend la structure spatiale des lignes et des colonnes de pixels en entrée, extrait les caractéristiques via plusieurs couches de calcul mathématique, puis convertit le signal en un vecteur de caractéristiques et le connecte à la structure d'un réseau neuronal traditionnel après l'extraction des caractéristiques. , l'image Le vecteur de caractéristiques correspondant est plus petit lorsqu'il est fourni à un réseau neuronal traditionnel, et le nombre de paramètres à entraîner sera réduit en conséquence. Le schéma de principe de fonctionnement de base du réseau neuronal convolutif est le suivant (le numéro de chaque couche dans le diagramme peut être conçu selon les besoins) :

Sélection du framework

La raison pour laquelle le framework Tensorflow.js est devenu notre préféré framework est dû aux avantages suivants :

Bonne portabilité : Tensorflow.js n'est pas le framework d'apprentissage automatique le plus populaire et le plus efficace, mais comme il est basé sur JS et dispose d'une API prête à l'emploi, il est facile de exécuter et déployer sur divers terminaux prenant en charge JS.

Faible latence et confidentialité élevée : grâce au fait qu'il peut fonctionner complètement à la fin, il n'est pas nécessaire d'envoyer des données de vérification au serveur et d'attendre que le serveur réponde, bénéficiant ainsi des avantages d'une faible latence et d'une haute sécurité .

Faible coût d'apprentissage/débogage : le coût de démarrage est faible pour les développeurs WEB, et le navigateur peut bien visualiser le processus de formation de la machine.

La configuration de l'environnement de TFJS [2] est très simple et est omise ici.

Formation sur modèle

Vous pouvez découvrir des idées de programmation d'apprentissage automatique grâce à cet exemple simple et vous familiariser avec l'API de Tensorflow.js.

Ensemble de données

 /** * @license* Copyright 2018 Google LLC. All Rights Reserved. * Licensed under the Apache License, Version 2.0 (the "License"); * you may not use this file except in compliance with the License. * You may obtain a copy of the License at * * http://www.apache.org/licenses/LICENSE-2.0 * * Unless required by applicable law or agreed to in writing, software * distributed under the License is distributed on an "AS IS" BASIS, * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. * See the License for the specific language governing permissions and * limitations under the License. * ============================================================================= */ 
 const IMAGE_SIZE = 784;
 const NUM_CLASSES = 10;
 const NUM_DATASET_ELEMENTS = 65000;
 
 const NUM_TRAIN_ELEMENTS = 55000;
 const NUM_TEST_ELEMENTS = NUM_DATASET_ELEMENTS - NUM_TRAIN_ELEMENTS;
 
 const MNIST_IMAGES_SPRITE_PATH =
 'https://storage.googleapis.com/learnjs-data/model-builder/mnist_images.png';
 const MNIST_LABELS_PATH =
 'https://storage.googleapis.com/learnjs-data/model-builder/mnist_labels_uint8';
 
 /** * A class that fetches the sprited MNIST dataset and returns shuffled batches. * * NOTE: This will get much easier. For now, we do data fetching and * manipulation manually. */export class MnistData {
 constructor() {
 this.shuffledTrainIndex = 0;
 this.shuffledTestIndex = 0;
 }
 
 async load() {
 // Make a request for the MNIST sprited image.const img = new Image();
 const canvas = document.createElement('canvas');
 const ctx = canvas.getContext('2d');
 const imgRequest = new Promise((resolve, reject) => {
 img.crossOrigin = '';
 img.onload = () => {
 img.width = img.naturalWidth;
 img.height = img.naturalHeight;
 
 const datasetBytesBuffer =
 new ArrayBuffer(NUM_DATASET_ELEMENTS * IMAGE_SIZE * 4);
 
 const chunkSize = 5000;
 canvas.width = img.width;
 canvas.height = chunkSize;
 
 for (let i = 0; i < NUM_DATASET_ELEMENTS / chunkSize; i++) {
 const datasetBytesView = new Float32Array(
 datasetBytesBuffer, i * IMAGE_SIZE * chunkSize * 4,
 IMAGE_SIZE * chunkSize);
 ctx.drawImage(
 img, 0, i * chunkSize, img.width, chunkSize, 0, 0, img.width,
 chunkSize);
 
 const imageData = ctx.getImageData(0, 0, canvas.width, canvas.height);
 
 for (let j = 0; j < imageData.data.length / 4; j++) {
 // All channels hold an equal value since the image is grayscale, so// just read the red channel.datasetBytesView[j] = imageData.data[j * 4] / 255;
 }
 }
 this.datasetImages = new Float32Array(datasetBytesBuffer);
 
 resolve();
 };
 img.src = MNIST_IMAGES_SPRITE_PATH;
 });
 
 const labelsRequest = fetch(MNIST_LABELS_PATH);
 const [imgResponse, labelsResponse] =
 await Promise.all([imgRequest, labelsRequest]);
 
 this.datasetLabels = new Uint8Array(await labelsResponse.arrayBuffer());
 
 // Create shuffled indices into the train/test set for when we select a// random dataset element for training / validation.this.trainIndices = tf.util.createShuffledIndices(NUM_TRAIN_ELEMENTS);
 this.testIndices = tf.util.createShuffledIndices(NUM_TEST_ELEMENTS);
 
 // Slice the the images and labels into train and test sets.this.trainImages =
 this.datasetImages.slice(0, IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
 this.testImages = this.datasetImages.slice(IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
 this.trainLabels =
 this.datasetLabels.slice(0, NUM_CLASSES * NUM_TRAIN_ELEMENTS);
 this.testLabels =
 this.datasetLabels.slice(NUM_CLASSES * NUM_TRAIN_ELEMENTS);
 }
 
 nextTrainBatch(batchSize) {
 return this.nextBatch(
 batchSize, [this.trainImages, this.trainLabels], () => {
 this.shuffledTrainIndex =
 (this.shuffledTrainIndex + 1) % this.trainIndices.length;
 return this.trainIndices[this.shuffledTrainIndex];
 });
 }
 
 nextTestBatch(batchSize) {
 return this.nextBatch(batchSize, [this.testImages, this.testLabels], () => {
 this.shuffledTestIndex =
 (this.shuffledTestIndex + 1) % this.testIndices.length;
 return this.testIndices[this.shuffledTestIndex];
 });
 }
 
 nextBatch(batchSize, data, index) {
 const batchImagesArray = new Float32Array(batchSize * IMAGE_SIZE);
 const batchLabelsArray = new Uint8Array(batchSize * NUM_CLASSES);
 
 for (let i = 0; i < batchSize; i++) {
 const idx = index();
 
 const image =
 data[0].slice(idx * IMAGE_SIZE, idx * IMAGE_SIZE + IMAGE_SIZE);
 batchImagesArray.set(image, i * IMAGE_SIZE);
 
 const label =
 data[1].slice(idx * NUM_CLASSES, idx * NUM_CLASSES + NUM_CLASSES);
 batchLabelsArray.set(label, i * NUM_CLASSES);
 }
 
 const xs = tf.tensor2d(batchImagesArray, [batchSize, IMAGE_SIZE]);
 const labels = tf.tensor2d(batchLabelsArray, [batchSize, NUM_CLASSES]);
 
 return {xs, labels};
 }
 }

 // 我们直接使用mnist数据集这个经典的手写数字数据集，节约了收集手写数字的Créez vos propres événements interactifs - reconnaissance des gestes sur écran集的时间
import {MnistData} from './data.js';

let cnnModel=null;

async function run() {
// 加载数据集 const data = new MnistData();
await data.load();
// 构造模型，设置模型参数 cnnModel = getModel();
// 训练模型 await train(cnnModel, data);
}

function getModel() {
const model = tf.sequential();

const IMAGE_WIDTH = 28;
const IMAGE_HEIGHT = 28;
const IMAGE_CHANNELS = 1;

// 在第一层，指定输入数据的形状，设置卷积参数 model.add(tf.layers.conv2d({
// 流入模型第一层的数据的形状。在本例中，我们的 MNIST 示例是 28x28 像素的黑白Créez vos propres événements interactifs - reconnaissance des gestes sur écran。Créez vos propres événements interactifs - reconnaissance des gestes sur écran数据的规范格式为 [row, column, depth] inputShape: [IMAGE_WIDTH, IMAGE_HEIGHT, IMAGE_CHANNELS],
// 要应用于输入数据的滑动卷积过滤器窗口的尺寸。在此示例中，我们将kernelSize设置成5，也就是指定 5x5 的卷积窗口。 kernelSize: 5,
// 尺寸为 kernelSize 的过滤器窗口数量 filters: 8,
// 滑动窗口的步长，即每次移动Créez vos propres événements interactifs - reconnaissance des gestes sur écran时过滤器都会移动多少像素。我们指定步长为 1，表示过滤器将以 1 像素为步长在Créez vos propres événements interactifs - reconnaissance des gestes sur écran上滑动。 strides: 1,
// 卷积完成后应用于数据的激活函数。在本例中，我们将应用修正线性单元 (ReLU) 函数，这是机器学习模型中非常常见的激活函数。 activation: 'relu',
// 通常使用 VarianceScaling作为随机初始化模型权重的方法 kernelInitializer: 'varianceScaling'
}));

// MaxPooling最大池化层使用区域最大值而不是平均值进行降采样 model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));

// 重复一遍conv2d + maxPooling // 注意这次卷积的过滤器窗口数量更多 model.add(tf.layers.conv2d({
kernelSize: 5,
filters: 16,
strides: 1,
activation: 'relu',
kernelInitializer: 'varianceScaling'
}));
model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));

// 现在我们将2维滤波器的输出展平为1维向量，作为最后一层的输入。这是将高维数据输入给最后的分类输出层时的常见做法。 // Créez vos propres événements interactifs - reconnaissance des gestes sur écran是高维数据，而卷积运算往往会增大传入其中的数据的大小。在将数据传递到最终分类层之前，我们需要将数据展平为一个长数组。密集层（我们会用作最终层）只需要采用 tensor1d，因而此步骤在许多分类任务中很常见。 // 注意：展平层中没有权重。它只是将其输入展开为一个长数组。 model.add(tf.layers.flatten());

// 计算我们的最终概率分布，我们将使用密集层计算10个可能的类的概率分布，其中得分最高的类将是预测的数字。 const NUM_OUTPUT_CLASSES = 10;
model.add(tf.layers.dense({
units: NUM_OUTPUT_CLASSES,
kernelInitializer: 'varianceScaling',
activation: 'softmax'
}));

// 模型编译，选择优化器，损失函数categoricalCrossentropy，和精度指标accuracy（正确预测在所有预测中所占的百分比），然后编译并返回模型 const optimizer = tf.train.adam();
model.compile({
optimizer: optimizer,
loss: 'categoricalCrossentropy',
metrics: ['accuracy'],
});

return model;
}

// 我们的目标是训练一个模型，该模型会获取一张Créez vos propres événements interactifs - reconnaissance des gestes sur écran，然后学习预测Créez vos propres événements interactifs - reconnaissance des gestes sur écran可能所属的 10 个类中每个类的得分（数字 0-9）。 async function train(model, data) {
const metrics = ['loss', 'val_loss', 'acc', 'val_acc'];
const container = {
name: 'Model Training', tab: 'Model', styles: { height: '1000px' }
};
const fitCallbacks = tfvis.show.fitCallbacks(container, metrics);

const BATCH_SIZE = 512;
const TRAIN_DATA_SIZE = 5500;
const TEST_DATA_SIZE = 1000;

const [trainXs, trainYs] = tf.tidy(() => {
const d = data.nextTrainBatch(TRAIN_DATA_SIZE);
return [
d.xs.reshape([TRAIN_DATA_SIZE, 28, 28, 1]),
d.labels
];
});

const [testXs, testYs] = tf.tidy(() => {
const d = data.nextTestBatch(TEST_DATA_SIZE);
return [
d.xs.reshape([TEST_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
// 设置特征和标签 return model.fit(trainXs, trainYs, {
batchSize: BATCH_SIZE,
validationData: [testXs, testYs],
epochs: 10, //训练轮次 shuffle: true,
callbacks: fitCallbacks
});
}

Déploiement et fonctionnement du modèle

 // 预测canvas上画的图形属于哪个分类 function predict(){
const input = tf.tidy(() => {
return tf.image
.resizeBilinear(tf.browser.fromPixels(canvas), [28, 28], true)
.slice([0, 0, 0], [28, 28, 1])
.toFloat()
.div(255)
.reshape([1, 28, 28, 1]);
});
const pred = cnnModel.predict(input).argMax(1);
console.log('预测结果为', pred.dataSync())
alert(`预测结果为 ${pred.dataSync()[0]}`);
};

document.getElementById('predict-btn').addEventListener('click', predict)
document.getElementById('clear-btn').addEventListener('click', clear)
document.addEventListener('DOMContentLoaded', run);

const canvas = document.querySelector('canvas');
canvas.addEventListener('mousemove', (e) => {
if (e.buttons === 1) {
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(255,255,255)';
ctx.fillRect(e.offsetX, e.offsetY, 10, 10);
}
});

function clear(){
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(0,0,0)';
ctx.fillRect(0, 0, 300, 300);
};

clear();

Évaluation du programme

L'avantage de ce programme est que plus l'ensemble de données impliqué dans la formation est grand, meilleur est l'effet de prédiction. Ses inconvénients sont également évidents. Premièrement, la construction de l'ensemble de données de formation et de l'ensemble de données de vérification représente une énorme quantité de travail. De plus, même si la formation peut être effectuée pendant que le navigateur est en cours d'exécution, elle prend toujours du temps. En résumé, cette solution peut détecter plusieurs gestes prédéfinis, mais il est difficile de former un modèle capable de reconnaître les gestes spécifiques de l'utilisateur via plusieurs entrées gestuelles de l'utilisateur.

Autres questions

La méthode OCR de reconnaissance de l'écriture manuscrite peut-elle être utilisée pour reconnaître les gestes définis par l'utilisateur ?

En raison de l'incertitude de la saisie utilisateur, les gestes saisis par l'utilisateur ne correspondent pas nécessairement à une catégorie prédéfinie spécifique. La classification des images peut-elle déterminer « d'autres » catégories ?

Le format du modèle Tensorflow est-il lié au langage framework ? Par exemple, le modèle entraîné par python peut-il toujours être utilisé dans tensorflow.js ?

​Utilisation de la méthode d'analyse géométrique​

Idée de base

Ce qui est récupéré lors de l'interaction avec la souris, ce sont des informations sur le chemin. Grâce à ces informations sur le chemin, nous pouvons extraire des informations plus spécifiques telles que la position, la forme, la direction, etc. Par conséquent, nous pouvons enregistrer la trajectoire spatio-temporelle de la souris, puis utiliser des règles pour résumer les caractéristiques du chemin du geste, le solidifier en un modèle qui peut identifier de manière unique le geste avec une forte probabilité, puis comparer la similitude entre le modèle de geste et gestes ordinaires. Notez que lors de la définition de la structure des données de chemin, vous devez envisager d'éviter les effets de taille et de légère déformation.

Extraction et enregistrement des caractéristiques du chemin

Tout d'abord, le chemin gestuel dessiné par l'utilisateur doit être représenté. Nous clarifions un principe de base selon lequel les objets ayant la même forme mais des tailles différentes doivent être considérés comme le même geste. Le chemin gestuel doit être représenté par un ensemble de vecteurs unitaires. Dans Stroke, le graphique gestuel est divisé en 128 vecteurs et chaque vecteur est converti en vecteur unitaire. De cette façon, même si la taille et la longueur des trajectoires gestuelles sont différentes, tant qu'elles sont structurellement identiques, les données qui les représentent seront les mêmes. Cela élimine l'influence de la taille du chemin et de la légère déformation sur les résultats du jugement.

Représentation de la similarité des caractéristiques du chemin

Ensuite, la similarité du chemin mesuré est convertie en similarité des données vectorielles mesurées. La similarité entre les chemins est déterminée par la valeur spécifique d'une quantité géométrique, nous avons donc trouvé la similarité cosinusoïdale à partir de la méthode classique de calcul de la similarité vectorielle.

向量的相似度通常使用余弦相似度来度量，即计算向量夹角的余弦值。将两组数据两两对应，分成128组向量，每组2个，计算每组向量的余弦值并累加。最终得到的结果应该会在 [-128, 128] 之间，数值越大也就表示相似度越高。我们只需设置一个阈值，超过这个阈值的就认为匹配成功。

为了计算两个向量夹角的余弦值，引入向量的点乘，根据向量点乘公式（推导过程[3]）：

这里|a|表示向量a的模（长度），θ表示两个向量之间的夹角。

两个互相垂直的向量的点积总是零。若向量a和b都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。那么，给定两个向量，它们之间的夹角可以通过下列公式得到：

这个运算可以简单地理解为：在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

对于二维向量，我们用一个[number, number]元组来表示。

核心实现逻辑：

import { useEffect, useState, useRef, useMemo } from 'react'
import throttle from "lodash/throttle"

type Position = {x:number, y:number};
type Vector = [number, number];

// 预先定义特殊V字型的手势路径，便于调试。 const shapeVectors_v: Vector[] = [[5,16],[13,29],[4,9],[6,9],[8,8],[1,0],[1,0],[1,-2],[0,-3],[7,-11],[21,-34],[10,-19]];
const shapeVectors_l: Vector[] = [[0,15],[0,33],[0,19],[0,4],[0,3],[0,8],[2,6],[11,0],[28,0],[18,0],[5,0],[1,0]]
const shapeVectors_6: Vector[] = [[-41,18],[-40,33],[-30,39],[-24,62],[1,53],[40,27],[38,2],[30,-34],[7,-41],[-31,-21],[-38,-4],[-19,0]];
const shapeVectors: {[key:string]: Vector[]} = {
v: shapeVectors_v,
l: shapeVectors_l,
6: shapeVectors_6
}

function Gesture(){
const pointsRef = useRef<Position[]>([]);
const sparsedPointsRef = useRef<Position[]>([]);
const vectorsRef = useRef<Vector[]>([]);

const canvasContextRef = useRef<CanvasRenderingContext2D>()
const containerRef = useRef<HTMLDivElement>(null)

const [predictResults, setPredictResults] = useState<{label: string, similarity: number}[]>([])

// 按一定的时间间隔采集点 const handleMouseMoveThrottled = useMemo(()=>{return throttle(handleMouseMove, 16)}, [canvasContextRef.current])

useEffect(()=>{
const canvasEle = document.getElementById('canvas-ele') as HTMLCanvasElement;
const ctx = canvasEle.getContext('2d')!;
canvasContextRef.current=ctx;
handleClear();
}, [])

function handleMouseDown(){
containerRef?.current?.addEventListener('mousemove', handleMouseMoveThrottled);
}

function handleMouseUp(){
console.log('up')
containerRef?.current?.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
pointsRef.current=[]
}

// 为了方便示意，我们把鼠标路径可视化出来。 function drawPoint(x:number,y:number){
// console.log(x, y) // canvasContext?.arc(x, y, 5, 0, Math.PI*2); (canvasContextRef.current!).fillStyle = 'red';
canvasContextRef.current?.fillRect(x, y, 10,10)
}

// 鼠标滑过时，记录下一串间隔的点。 function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
drawPoint(x, y)
const newPoints = [...pointsRef.current, {x,y}];
pointsRef.current = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPointsRef.current=sparsedNewPoints;
const vectors = points2Vectors(sparsedNewPoints)
vectorsRef.current = vectors;
console.log('points', x, y)
// const angles = vectors.map(vector2PolarAngle) // console.log('angles', angles[angles.length-1]) }

// 如果点太多，处理起来性能不佳，除了节流之外，我们始终将点抽稀到13个（我们假设每个手势的持续时间都不低于200ms，能保证在节流16ms的情况下，至少收集到13个原始点，这样抽稀才有意义） // 抽稀的策略是以固定的间隔平均抽，这样有个潜在问题：如果用户划手势时速度不够均匀，比如在同一个手势路径中某段时间划的速度比较快（点会比较密集），在某段时间的速度比较慢（点会比较稀疏），那由抽稀后的点构造出的路径向量就会比较失真，影响最终判断的准确性。 // 优化的方案是在空间上采用分区抽稀的策略，避免用户手速不均匀导致的问题，但分区逻辑比较复杂，我们暂且按下不做深入研究。 // todo: 抽稀后，相邻的点不能重复，否则会有0向量、对运算和判断造成干扰。 function sparsePoints(points: Position[]){
const sparsedLength = 13;
if(points.length<=sparsedLength){
return points;
}else{
let sparsedPoints = [];
let step = points.length/sparsedLength;
for(let i=0; i<sparsedLength; i++){
const curIndex = Math.round(step*i);
sparsedPoints.push(points[curIndex])
}
return sparsedPoints;
}
}

// 对于非闭合的路径，手势方向会影响判断逻辑，相同的路径可能是由相反的手势方向画出来的。比如L形的手势。 // 对于闭合的路径，手势的方向和起止位置都会影响判断逻辑，相同的路径可能是由相反的手势方向画出来的，也可能是由不同起始位置画出来的。比如圆形的手势。 // 为了消除相同路径不同画法的影响，我们做如下处理 
function normalizePoints(points:Position[]){
// if (是闭合路径) 将位置在最左上角的点作为数组的第一位，其余的依次排列，然后返回 // else 原样返回 return points;
}

// 相邻的两个点相连，生成一个向量。用这n个点的坐标生成n-1个向量，这n-1个向量组成一段路径，用来表示一个鼠标手势。 function points2Vectors(points: Position[]){
if(points.length<=1){
return []
}else{
return points.reduce((pre:Vector[], cur, curIdx)=>{
if(curIdx===0){return []}
const prePoint = points[curIdx-1];
const vec:Vector = [cur.x-prePoint.x, cur.y-prePoint.y];
return [...pre, vec];
}, [])
}
}

// 判断两条路径是否是相同，保证组成两条路径的向量数相同，然后计算两条路径对应向量的余弦相似度（取值在-1~1之间，越接近-1或者1，越相似）。最后再与定义的阈值比较，超过阈值就认为路径相同。 function judge(vec1:Vector[], vec2: Vector[], threshold?:number){
// 暂定阈值为0.5 const finalThreshold = threshold||0.5;
// 为消除路径方向的影响（一个向量与另一个反向相反的向量的余弦值是-1，应该认为它们形状相同），反转路径后再次判断 return cosineSimilarity(vec1, vec2)>=finalThreshold || cosineSimilarity(vec1, vec2.reverse())>=finalThreshold
}

// 两组向量的余弦相似度，保证组成两条路径的向量数相同，然后计算两条路径对应向量的余弦值，累加取均值.取值在-1~1之间，越接近-1或者1，越相似. function cosineSimilarity(vec1: Vector[], vec2: Vector[]){
if(vec1.length!==vec2.length){
console.warn('进行比较的两个路径长度（路径内的向量数）必须一致')
return 0;
}else{
let cosValueSum = 0;
vec1.forEach((v1, i)=>{
cosValueSum+=vectorsCos(v1, vec2[i])
})
// 取余弦值的绝对值，绝对值越接近1，相似度越高。 const cosValueRate = Math.abs(cosValueSum/vec1.length);
console.log('cosValueRate', cosValueRate)
return cosValueRate;
}
}

// 两个向量的余弦值 function vectorsCos(v1:Vector, v2:Vector){
// 特殊情况，0向量的余弦值我们认为是1 if(vectorLength(v1)*vectorLength(v2)===0){
return 1;
}
return vectorsDotProduct(v1, v2)/(vectorLength(v1)*vectorLength(v2));
}

// 向量的点乘 function vectorsDotProduct(v1:Vector, v2:Vector){
return v1[0]*v2[0]+v1[1]*v2[1];
}
// 向量的长度 function vectorLength(v:Vector){
return Math.sqrt(Math.pow(v[0], 2)+Math.pow(v[1], 2))
}

// 向量归一化，消除向量在长度上的差异，控制变量，方便训练机器学习模型(https://zhuanlan.zhihu.com/p/424518359) function normalizeVector(vec:Vector){
const length = Math.sqrt(Math.pow(vec[0],2)+Math.pow(vec[1], 2))
return [vec[0]/length, vec[1]/length]
}

function handlePredict(){
const results = Object.keys(shapeVectors).map(key=>({
label: key,
similarity: cosineSimilarity(shapeVectors[key], vectorsRef.current),
}))
setPredictResults(results);
console.log('results', results)
}

function handleClear(){
pointsRef.current=[];
sparsedPointsRef.current=[];
vectorsRef.current=[];
(canvasContextRef.current!).fillStyle = 'rgb(0,0,0)';
(canvasContextRef.current!).fillRect(0, 0, 500, 500);
setPredictResults([]);
}

// 工程化封装，为某个dom元素增加自定义手势事件 function addCustomEvent(ele: HTMLElement, eventName: string, eventLisener:(...args:any[])=>any){
let points = [], sparsedPoints=[],vecs:Vector[]=[];
const customEvent = new Event(eventName);

function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
const newPoints = [...pointsRef.current, {x,y}];
points = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPoints=sparsedNewPoints;
const newVectors = points2Vectors(sparsedNewPoints)
vecs = newVectors;
console.log('points', x, y)
}

const handleMouseMoveThrottled = throttle(handleMouseMove, 16)

function handleMouseDown(){
ele.addEventListener('mousemove', handleMouseMoveThrottled);
}

function handleMouseUp(){
console.log('up')
ele.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
if(judge(vecs, shapeVectors['l'], 0.6)){
ele.dispatchEvent(customEvent)
}
points=[], sparsedPoints=[], vecs=[];
}

ele.addEventListener(eventName, eventLisener)
ele.addEventListener('mousedown', handleMouseDown);
ele.addEventListener('mouseup', handleMouseUp);

return function distroyEventListener(){
ele.removeEventListener(eventName, eventLisener)
}
}

return 
<canvas  width='500' height="500"></canvas>
<section>
<button notallow={handlePredict}>预测</button>
<button notallow={handleClear}>清空</button>
</section>
<ul>
{predictResults.map(e=>(
<li key={e.label}>
{`与 ${e.label}的相似度：${e.similarity}`}
</li>
))}
</ul>

}
export default Gesture

性能优化

点和向量的计算属于计算密集型任务，且其需要与主线程通信的数据量不大，考虑将其搬进webworker。此外，canvas的渲染性能也可以使用requestAnimationFrame和硬件加速来优化。属于常见的工程层面优化，此处略。

方案评价

余弦相似度的方法，优势在于计算量不大，可以在运行时由用户自定义手势，且所需保存的数据量不大，也适合网络传输。劣势在于难以衡量复杂多笔画、没有严格笔顺的图形的相似度。

​扩展到三维空间​

针对二维平面内的手势识别方案如何扩展到三维空间呢？比如在VR/MR场景内，手势路径会是一组三维向量，如果我们能将余弦相似度的适用范围扩展到三维向量，也就顺理成章地解决了这个问题。

基本思路就是分别分析两个三维向量在xoy平面上的投影之间的夹角以及在yoz平面上的投影之间的夹角的余弦相似度，将两者的乘积作为两个三维向量之间的余弦相似度。判断逻辑与二维向量的一致。

​综合方案​

综合考虑机器学习的方案和几何分析方案的优劣势，我们做如下设计。对于预设的手势，我们构造数据集、离线训练模型，然后将模型内置在产品内。对于自定义的手势，我们采用几何分析方案，让用户连续输入3次，先计算每次输入的路径的两两之间的相似度，且选出相似度的最小值n，如果最小值n大于某个阈值m，且每次输入的路径与其他已有路径的相似度均小于m时，我们就将距离其余两条路径的相似度之和最小的那条路径作为用户自定义的新路径，n作为其相似度判断的阈值。

参考资料

[1]预训练好的模型: https://github.com/tensorflow/tfjs-models

[2]环境搭建: https://github.com/tensorflow/tfjs#getting-started

[3]推导过程: https://blog.csdn.net/dcrmg/article/details/52416832

[4]复杂鼠标手势的识别是如何实现的? - 知乎: https://www.zhihu.com/question/20607813

[5]点积相似度、余弦相似度、欧几里得相似度: https://zhuanlan.zhihu.com/p/159244903

[6]机器学习并没有那么深奥，它还很有趣（1）-36氪: https://m.36kr.com/p/1721248956417

[7]计算向量间相似度的常用方法: https://cloud.tencent.com/developer/article/1668762

[8]C#手势库的核心逻辑实现: https://github.com/poerin/Stroke/blob/master/Stroke/Gesture.cs

[9]什么是张量 (tensor)? - 知乎: https://www.zhihu.com/question/20695804

[10]使用 CNN 识别手写数字: https://codelabs.developers.google.com/codelabs/tfjs-training-classfication?hl=zh-cn#0

[11]机器学习: https://zh.m.wikipedia.org/zh/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0

[12]文字识别方法整理（2015~2019）: https://zhuanlan.zhihu.com/p/65707543

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!