Les essentiels du machine learning : comment éviter le surapprentissage ?

En fait, l'essence de la régularisation est très simple. Il s'agit d'un moyen ou d'une opération qui impose des restrictions ou des contraintes a priori sur un certain problème pour atteindre un objectif spécifique. Le but de l’utilisation de la régularisation dans un algorithme est d’empêcher le surajustement du modèle. Lorsqu'il s'agit de régularisation, de nombreux étudiants peuvent immédiatement penser à la norme L1 et à la norme L2 couramment utilisées. Avant de résumer, voyons d'abord ce qu'est la norme LP ? La

norme LP

norme peut simplement être comprise comme utilisée pour représenter la distance dans l'espace vectoriel, et la définition de la distance est très abstraite tant qu'elle satisfait aux inégalités non négatives, réflexives et triangulaires, elle peut être appelée distance.

La norme LP n'est pas une norme, mais un ensemble de normes, qui est défini comme suit :

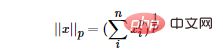
La plage de p est [1,∞). p n'est pas défini comme une norme dans la plage de (0,1) car il viole l'inégalité triangulaire.

Selon le changement de pp, la norme change également différemment. En empruntant un diagramme classique de changement de norme P comme suit :

L'image ci-dessus montre que lorsque p passe de 0 à l'infini positif, la boule unité (unité). balle) change. La boule unitaire définie sous la norme P est un ensemble convexe, mais lorsque 0

Alors la question est : quelle est la norme L0 ? La norme L0 représente le nombre d'éléments non nuls dans le vecteur et est exprimée par la formule suivante :

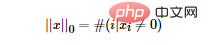
Nous pouvons trouver le terme de caractéristique clairsemé le moins optimal en minimisant la norme L0. Mais malheureusement, le problème d’optimisation de la norme L0 est un problème NP difficile (la norme L0 est également non convexe). Par conséquent, dans les applications pratiques, nous effectuons souvent une relaxation convexe de L0. Il est théoriquement prouvé que la norme L1 est l’approximation convexe optimale de la norme L0, donc la norme L1 est généralement utilisée au lieu d’optimiser directement la norme L0.

Norme L1

Selon la définition de la norme LP, nous pouvons facilement obtenir la forme mathématique de la norme L1 :

Comme vous pouvez le voir dans la formule ci-dessus, la norme L1 est la somme des valeurs absolues de chaque élément du vecteur, également appelé « Opérateur de régularisation clairsemée » (régularisation Lasso). La question est donc : pourquoi voulons-nous une sparsification ? Les avantages de la sparsification sont nombreux, les deux plus directs sont :

• Sélection des caractéristiques
• Interprétabilité

Norme L2

La norme L2 est la plus familière, c'est la distance euclidienne, la formule est la suivante :

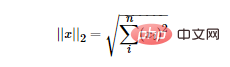
La norme L2 a plusieurs noms. Certaines personnes appellent sa régression « Ridge Regression », tandis que d'autres l'appellent « Weight Decay ». Utiliser la norme L2 comme terme de régularisation peut obtenir une solution dense, c'est-à-dire que le paramètre ww correspondant à chaque caractéristique est très petit, proche de 0 mais pas 0 de plus, la norme L2 comme terme de régularisation peut empêcher le modèle de ; s'adapter à l'ensemble de formation. Trop de complexité conduit à un surajustement, améliorant ainsi la capacité de généralisation du modèle.

La différence entre la norme L1 et la norme L2

Introduisez un diagramme classique de PRML pour illustrer la différence entre la norme L1 et la norme L2, comme indiqué ci-dessous :

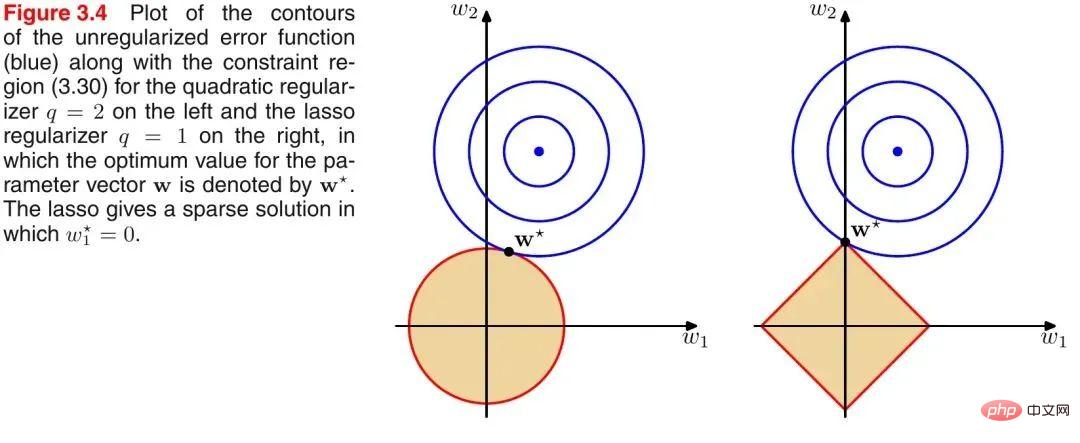
Comme le montre l'image ci-dessus, le cercle bleu indique la plage de solutions possibles du problème, et la couleur orange indique la plage de solutions possibles du terme régulier. La fonction objectif entière (problème original + terme régulier) a une solution si et seulement si les deux plages de solutions sont tangentes. Il est facile de voir sur la figure ci-dessus que puisque la plage de solution de la norme L2 est un cercle, le point tangent n'est probablement pas sur l'axe des coordonnées, et puisque la norme L1 est un losange (le sommet est convexe), son point tangent Le point tangent est plus susceptible d'être sur l'axe des coordonnées, et le point sur l'axe des coordonnées a une caractéristique selon laquelle un seul composant de coordonnées est différent de zéro et les autres composants de coordonnées sont nuls, c'est-à-dire qu'il est clairsemé. Nous avons donc la conclusion suivante : la norme L1 peut conduire à des solutions clairsemées, et la norme L2 peut conduire à des solutions denses.

D'un point de vue bayésien a priori, lors de la formation d'un modèle, il ne suffit pas de s'appuyer uniquement sur l'ensemble de données de formation actuel. Afin d'obtenir de meilleures capacités de généralisation, il est souvent nécessaire d'ajouter des termes antérieurs, et l'ajout de termes réguliers équivaut à. A priori a été ajouté.

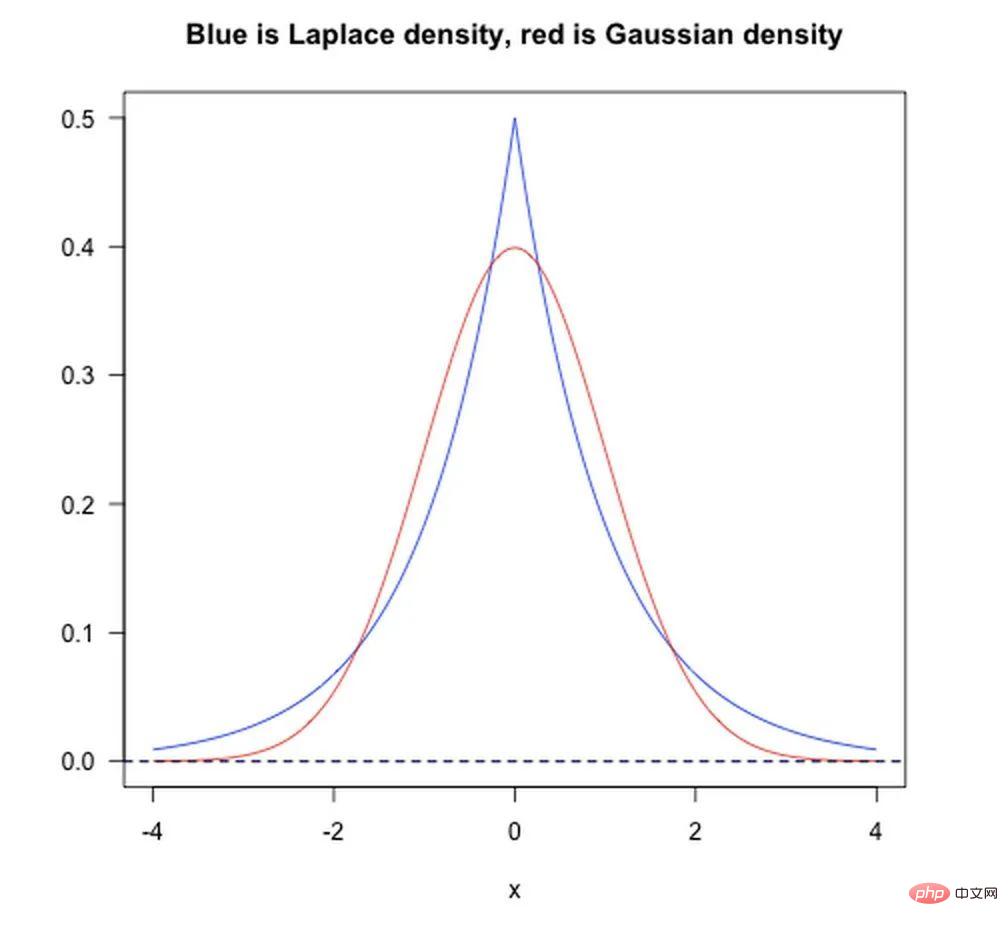
• La norme L1 équivaut à l'ajout d'un a priori laplacéen ;
• La norme L2 équivaut à l'ajout d'un a priori gaussien ;

Comme le montre la figure ci-dessous :

Dropout

Dropout est une méthode de régularisation souvent utilisée en apprentissage profond. Son approche peut être simplement comprise comme la suppression de certains neurones avec une probabilité p pendant le processus de formation des DNN, c'est-à-dire que la sortie des neurones rejetés est égale à 0. Le dropout peut être instancié comme le montre la figure ci-dessous :

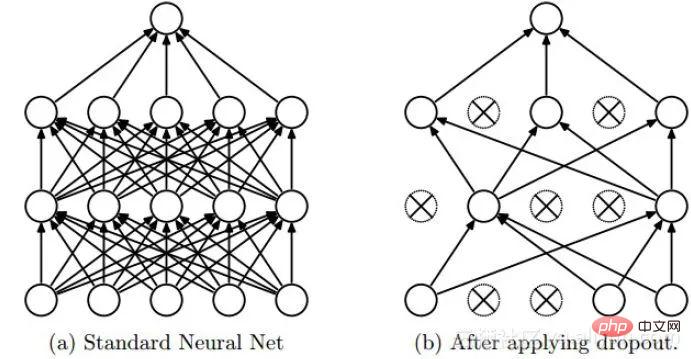
Nous pouvons intuitivement comprendre l'effet de régularisation du dropout sous deux aspects :

• L'opération consistant à perdre aléatoirement des neurones au cours de chaque cycle d'entraînement au dropout est équivalente à plusieurs DNN sont en moyenne, ils ont donc pour effet de voter lorsqu'ils sont utilisés à des fins de prédiction.
• Réduire la co-adaptation complexe entre les neurones. Lorsque les neurones de la couche cachée sont supprimés de manière aléatoire, le réseau entièrement connecté devient clairsemé dans une certaine mesure, réduisant ainsi efficacement les effets synergiques des différentes fonctionnalités. En d’autres termes, certaines fonctionnalités peuvent s’appuyer sur l’action conjointe de nœuds cachés avec des relations fixes, et grâce au Dropout, cela organise efficacement la situation dans laquelle certaines fonctionnalités ne sont efficaces qu’en présence d’autres fonctionnalités, augmentant ainsi la robustesse du réseau neuronal. sexe.

Normalisation par lots

La normalisation par lots est strictement une méthode de normalisation, principalement utilisée pour accélérer la convergence du réseau, mais elle a également un certain degré d'effet de régularisation.

Voici une référence à l'explication du changement de covariable dans la réponse Zhihu du Dr Wei Xiushen.

Remarque : le contenu suivant est extrait de la réponse Zhihu du Dr Wei Xiushen. Tout le monde sait qu'une hypothèse classique de l'apprentissage automatique statistique est que « la distribution des données (distribution) de l'espace source (domaine source) et de l'espace cible (domaine cible) est cohérent ». S’ils sont incohérents, de nouveaux problèmes d’apprentissage automatique surgissent, tels que l’apprentissage par transfert/adaptation de domaine, etc. Le changement de covariable est un problème de branche sous l'hypothèse d'une distribution incohérente. Cela signifie que les probabilités conditionnelles de l'espace source et de l'espace cible sont cohérentes, mais leurs probabilités marginales sont différentes. Si vous y réfléchissez bien, vous constaterez qu'en effet, pour les sorties de chaque couche du réseau de neurones, du fait qu'elles ont subi des opérations intra-couches, leur répartition est évidemment différente de la répartition des signaux d'entrée correspondant à chaque couche, et la différence augmentera à mesure que la profondeur du réseau augmente, mais les étiquettes d'échantillon qu'ils peuvent « indiquer » restent inchangées, ce qui répond à la définition du décalage covariable.

L'idée de base de BN est en fait assez intuitive, car la valeur d'entrée d'activation du réseau neuronal avant transformation non linéaire (X=WU+B, U est l'entrée) à mesure que la profondeur du réseau s'approfondit, sa distribution se déplace ou change progressivement (c'est-à-dire le changement de covariable mentionné ci-dessus). La raison pour laquelle l'entraînement converge lentement est généralement parce que la distribution globale se rapproche progressivement des limites supérieure et inférieure de la plage de valeurs de la fonction non linéaire (pour la fonction sigmoïde, cela signifie que la valeur d'entrée d'activation X = WU + B est un grand négatif ou valeur positive ), cela provoque donc la disparition du gradient du réseau neuronal de bas niveau lors de la rétro-propagation, ce qui est la raison essentielle pour laquelle la formation des réseaux neuronaux profonds converge de plus en plus lentement. BN utilise une certaine méthode de normalisation pour forcer la distribution de la valeur d'entrée de n'importe quel neurone dans chaque couche du réseau neuronal à revenir à la distribution normale standard avec une moyenne de 0 et une variance de 1, afin d'éviter le problème de dispersion du gradient provoqué par le fonction d'activation. Ainsi, plutôt que de dire que le rôle du BN est d’atténuer le décalage des covariables, il vaut mieux dire que le BN peut atténuer le problème de dispersion des gradients.

Normalisation, standardisation et régularisation

Nous avons déjà mentionné la régularisation, nous mentionnons ici brièvement la normalisation et la standardisation. Normalisation : le but de la normalisation est de trouver une certaine relation de mappage pour mapper les données d'origine sur l'intervalle [a, b]. Généralement, a et b prendront des combinaisons de [−1,1], [0,1]. Il existe généralement deux scénarios d'application :

• Convertir le nombre en un nombre décimal entre (0, 1)
• Convertir le nombre dimensionnel en un nombre sans dimension

Normalisation min-max couramment utilisée :

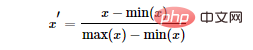
Standardisation : Utiliser le théorème des grands nombres pour transformer les données en une distribution normale standard. La formule de standardisation est :

.

La différence entre normalisation et standardisation :

Nous pouvons l'expliquer simplement ainsi : la mise à l'échelle normalisée est "aplatie" uniformément à l'intervalle (déterminée uniquement par des valeurs extrêmes), tandis que la mise à l'échelle normalisée est plus "élastique" et "dynamique" et a une grande relation avec la distribution de l’échantillon global. Remarque :

• Normalisation : la mise à l'échelle est uniquement liée à la différence entre les valeurs maximales et minimales.
• Standardisation : la mise à l'échelle est liée à chaque point et se reflète par la variance. Comparez cela avec la normalisation, à laquelle tous les points de données contribuent (par le biais de la moyenne et de l'écart type).

Pourquoi la standardisation et la normalisation ?

• Améliorez la précision du modèle : après la normalisation, les caractéristiques entre les différentes dimensions sont numériquement comparables, ce qui peut considérablement améliorer la précision du classificateur.
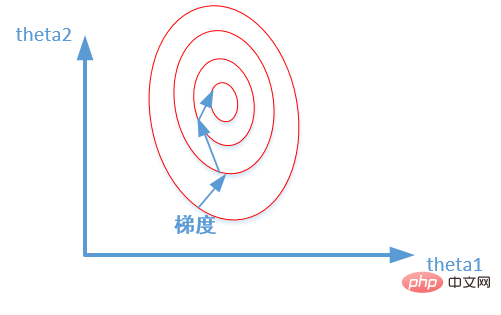
• Accélérer la convergence des modèles : après la standardisation, le processus d'optimisation de la solution optimale deviendra évidemment plus fluide, ce qui facilitera la convergence correcte vers la solution optimale. Comme le montre l'image ci-dessous :

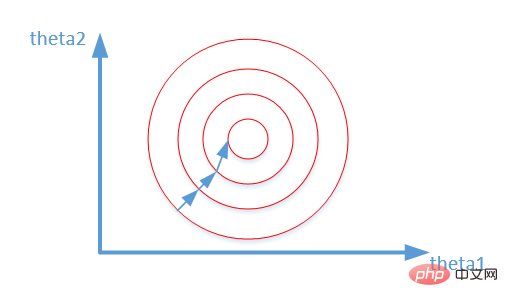
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!