Exemples opérationnels Python complets pour dix algorithmes de clustering

Le clustering ou analyse de cluster est un problème d'apprentissage non supervisé. Il est souvent utilisé comme technique d'analyse de données pour découvrir des modèles intéressants dans les données, tels que des segments de clientèle en fonction de leur comportement. Il existe de nombreux algorithmes de clustering parmi lesquels choisir, et il n’existe pas d’algorithme de clustering unique pour toutes les situations. Au lieu de cela, il est préférable d’explorer une gamme d’algorithmes de clustering et différentes configurations de chaque algorithme. Dans ce didacticiel, vous découvrirez comment installer et utiliser les meilleurs algorithmes de clustering en Python.

Après avoir terminé ce didacticiel, vous saurez :

• Le clustering est le problème non supervisé consistant à trouver des groupes naturels dans l'espace des caractéristiques des données d'entrée.
• Il existe de nombreux algorithmes de clustering différents et une seule meilleure méthode pour tous les ensembles de données.
• Comment implémenter, adapter et utiliser des algorithmes de clustering de haut niveau en Python avec la bibliothèque d'apprentissage automatique scikit-learn.

Présentation du didacticiel

1. Ce didacticiel est divisé en trois parties :
2. Clustering
3. Algorithme de clustering

• Exemple d'algorithme de clustering
• Installation de la bibliothèque
• Clustering Ensembles de données
• Propagation d'affinité
• Clustering agrégé
• BIRCH
• DBSCAN
• K-Means
• Mini-Batch K-Means
• Mean Shift
• OPTICS
• Spectral Clustering
• Modèle de mélange gaussien

1. Clustering

Clustering L'analyse, c'est-à-dire le clustering, est une méthode non supervisée tâche d'apprentissage automatique. Il inclut la découverte automatique de regroupements naturels dans les données. Contrairement à l'apprentissage supervisé (similaire à la modélisation prédictive), les algorithmes de clustering interprètent simplement les données d'entrée et trouvent des groupes ou clusters naturels dans l'espace des fonctionnalités.

• Les techniques de clustering conviennent lorsqu'il n'y a pas de classes à prédire, mais que les instances sont divisées en groupes naturels.
• —Extrait : "Page d'exploration de données : outils et techniques pratiques d'apprentissage automatique" 2016.

Un cluster est généralement une région de densité dans l'espace de fonctionnalités où les exemples (observations ou lignes de données) du domaine sont plus proches du cluster que les autres clusters. Un cluster peut avoir un centre (centroïde) qui est un espace de caractéristiques échantillon ou ponctuelle, et peut avoir des limites ou des plages.

• Ces clusters peuvent refléter un mécanisme à l'œuvre dans le domaine à partir duquel les instances sont tirées, ce qui rend certaines instances plus similaires les unes aux autres qu'elles ne le sont aux autres.
• —Extrait : "Page d'exploration de données : outils et techniques pratiques d'apprentissage automatique" 2016.

Le clustering peut aider, en tant qu'activité d'analyse de données, à en savoir plus sur le domaine problématique, connu sous le nom de découverte de modèles ou découverte de connaissances. Par exemple :

• L'arbre évolutif peut être considéré comme le résultat d'une analyse de cluster artificielle.
• La séparation des données normales des valeurs aberrantes ou des anomalies peut être considérée comme un problème de clustering.
• La séparation des clusters en fonction du comportement naturel est un problème de cluster, appelé marché ; segmentation.

Le clustering peut également être utilisé comme un type d'ingénierie de fonctionnalités, où des exemples existants et nouveaux peuvent être cartographiés et étiquetés comme appartenant à l'un des clusters identifiés dans les données. Bien qu'il existe de nombreuses mesures quantitatives spécifiques aux clusters, l'évaluation des clusters identifiés est subjective et peut nécessiter l'intervention d'experts dans le domaine. En règle générale, les algorithmes de clustering sont comparés de manière académique sur des ensembles de données synthétiques avec des clusters prédéfinis que l'algorithme est censé découvrir.

• Le clustering est une technique d'apprentissage non supervisée, il est donc difficile d'évaluer la qualité du résultat d'une méthode donnée.
• —Extrait de : "Page d'apprentissage automatique : une perspective probabiliste" 2012.

2. Algorithme de clustering

Il existe de nombreux types d'algorithmes de clustering. De nombreux algorithmes utilisent des mesures de similarité ou de distance entre des exemples dans l'espace de fonctionnalités pour découvrir des régions d'observation denses. Par conséquent, il est souvent recommandé d’étendre vos données avant d’utiliser un algorithme de clustering.

• Au cœur de tous les objectifs de l'analyse groupée se trouve le concept du degré de similitude (ou de dissemblance) entre les objets individuels regroupés. Les méthodes de clustering tentent de regrouper les objets en fonction d'une définition de similarité fournie aux objets.
• — Tiré de : Les éléments de l'apprentissage statistique : exploration de données, inférence et prédiction, 2016

Certains algorithmes de clustering nécessitent que vous spécifiiez ou deviniez le nombre de clusters à trouver dans les données, tandis que d'autres nécessitent des observations spécifiées. Le minimum distance entre laquelle un exemplaire peut être considéré comme « fermé » ou « connecté ». L'analyse de cluster est donc un processus itératif dans lequel les évaluations subjectives des clusters identifiés sont réinjectées dans les changements de configuration de l'algorithme jusqu'à ce que les résultats souhaités ou appropriés soient obtenus. La bibliothèque scikit-learn fournit un ensemble de différents algorithmes de clustering parmi lesquels choisir. 10 des algorithmes les plus populaires sont répertoriés ci-dessous :

Propagation par affinité ssian Mixture

1. Chaque algorithme offre tous deux un approche différente du défi de la découverte de groupes naturels dans les données. Il n’existe pas de meilleur algorithme de clustering, et il n’existe pas de moyen simple de trouver le meilleur algorithme pour vos données sans recourir à des expériences contrôlées. Dans ce didacticiel, nous verrons comment utiliser chacun de ces 10 algorithmes de clustering populaires de la bibliothèque scikit-learn. Ces exemples vous fourniront une base pour copier et coller les exemples et tester les méthodes sur vos propres données. Nous n’entrerons pas dans la théorie du fonctionnement des algorithmes, ni ne les comparerons directement. Creusons un peu plus profondément.
2. 3. Exemples d'algorithmes de clustering
3. Dans cette section, nous examinerons comment utiliser 10 algorithmes de clustering populaires dans scikit-learn. Cela comprend un exemple d'ajustement d'un modèle et un exemple de visualisation des résultats. Ces exemples permettent de coller et de copier dans votre propre projet et d'appliquer les méthodes à vos propres données.
4. 1. Installation de la bibliothèque
5. Tout d’abord, installons la bibliothèque. Ne sautez pas cette étape car vous devez vous assurer que la dernière version est installée. Vous pouvez installer le référentiel scikit-learn à l'aide du programme d'installation pip Python comme indiqué ci-dessous :

6. sudo pip install scikit-learn

Ensuite, confirmons que la bibliothèque a été installée et que vous utilisez une version moderne. Exécutez le script suivant pour afficher le numéro de version de la bibliothèque.

7. # 检查 scikit-learn 版本
   import sklearn
   print(sklearn.__version__)

Lorsque vous exécutez l'exemple, vous devriez voir le numéro de version suivant ou supérieur.

8. 0.22.1

2. Ensemble de données de clustering
9. Nous utiliserons la fonction make_classification () pour créer un ensemble de données de classification binaire de test. L'ensemble de données contiendra 1 000 exemples, avec deux fonctionnalités d'entrée et un cluster par classe. Ces clusters sont visibles en deux dimensions, nous pouvons donc tracer les données dans un nuage de points et colorer les points du tracé selon le cluster spécifié.
10. Cela aidera à comprendre dans quelle mesure les clusters sont identifiés, au moins sur le problème de test. Les clusters de ce problème de test sont basés sur des gaussiennes multivariées, et tous les algorithmes de clustering ne sont pas efficaces pour identifier ces types de clusters. Par conséquent, les résultats de ce didacticiel ne doivent pas être utilisés comme base pour comparer des méthodes générales. Vous trouverez ci-dessous des exemples de création et de synthèse d'ensembles de données de clustering synthétiques.

# 综合分类数据集
from numpy import where
from sklearn.datasets import make_classification
from matplotlib import pyplot
# 定义数据集
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 为每个类的样本创建散点图
for class_value in range(2):
# 获取此类的示例的行索引
row_ix = where(y == class_value)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

L'exécution de cet exemple créera un ensemble de données synthétiques clusterisées, puis créera un nuage de points des données d'entrée, avec des points colorés par des étiquettes de classe (clusters idéalisés). Nous pouvons clairement voir deux groupes de données différents en deux dimensions et espérons qu'un algorithme de clustering automatique pourra détecter ces regroupements.

Scatterplot d'un ensemble de données synthétiques clusterisées de points colorés regroupés connus

Ensuite, nous pouvons commencer à examiner des exemples d'algorithmes de clustering appliqués à cet ensemble de données. J'ai fait quelques tentatives minimes pour adapter chaque méthode à l'ensemble de données.

3. Propagation d'affinité

La propagation d'affinité consiste à trouver un ensemble d'exemples qui résume le mieux les données.

Nous avons conçu une méthode appelée « propagation d'affinité » qui sert de mesure d'entrée de similarité entre deux paires de points de données. Des messages à valeur réelle sont échangés entre les points de données jusqu'à ce qu'un ensemble d'exemples de haute qualité et les clusters correspondants émergent progressivement

—Tiré de : "En passant des messages entre les points de données" 2007.

Il est implémenté via la classe AffinityPropagation, la principale configuration à ajuster est de définir le "Dampening" de 0,5 à 1, peut-être même les "Préférences".

Exemples complets répertoriés ci-dessous.

# 亲和力传播聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AffinityPropagation
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AffinityPropagation(damping=0.9)
# 匹配模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

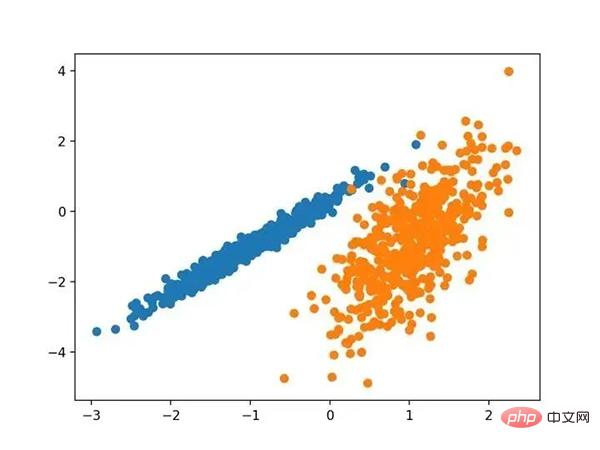Exécutez l'exemple pour ajuster le modèle sur l'ensemble de données d'entraînement et prédire le cluster pour chaque exemple de l'ensemble de données. Un nuage de points est ensuite créé, coloré par les clusters qui lui sont attribués. Dans ce cas, je ne parviens pas à obtenir de bons résultats.

Nuage de points d'un ensemble de données avec des clusters identifiés par propagation par affinité

4. Clustering agrégé

Le clustering agrégé implique la fusion d'exemples jusqu'à ce que le nombre souhaité de clusters soit atteint. Il fait partie d'une classe plus large de méthodes de clustering hiérarchique, implémentées via la classe AgglomerationClustering, et la configuration principale est l'ensemble " n_clusters ", qui est une estimation du nombre de clusters dans les données, par exemple 2. Un exemple complet est répertorié ci-dessous.

# 聚合聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AgglomerativeClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = AgglomerativeClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

• Exécutez l'exemple pour ajuster le modèle sur l'ensemble de données d'entraînement et prédire le cluster pour chaque exemple de l'ensemble de données. Un nuage de points est ensuite créé, coloré par les clusters qui lui sont attribués. Dans ce cas, un regroupement raisonnable peut être trouvé.

Nuage de points d'un ensemble de données avec des clusters identifiés à l'aide du clustering agglomératif

5.BIRCH

BIRCH 聚类（ BIRCH 是平衡迭代减少的缩写，聚类使用层次结构)包括构造一个树状结构，从中提取聚类质心。

• BIRCH 递增地和动态地群集传入的多维度量数据点，以尝试利用可用资源（即可用内存和时间约束）产生最佳质量的聚类。
• —源自：《 BIRCH ：1996年大型数据库的高效数据聚类方法》

它是通过 Birch 类实现的，主要配置是“ threshold ”和“ n _ clusters ”超参数，后者提供了群集数量的估计。下面列出了完整的示例。

# birch聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import Birch
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = Birch(threshold=0.01, n_clusters=2)
# 适配模型
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以找到一个很好的分组。

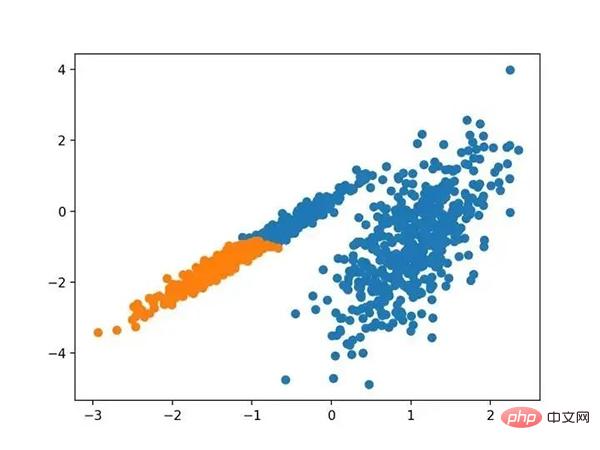
使用BIRCH聚类确定具有聚类的数据集的散点图

6.DBSCAN

DBSCAN 聚类（其中 DBSCAN 是基于密度的空间聚类的噪声应用程序）涉及在域中寻找高密度区域，并将其周围的特征空间区域扩展为群集。

• …我们提出了新的聚类算法 DBSCAN 依赖于基于密度的概念的集群设计，以发现任意形状的集群。DBSCAN 只需要一个输入参数，并支持用户为其确定适当的值
• -源自：《基于密度的噪声大空间数据库聚类发现算法》，1996

它是通过 DBSCAN 类实现的，主要配置是“ eps ”和“ min _ samples ”超参数。

下面列出了完整的示例。

# dbscan 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = DBSCAN(eps=0.30, min_samples=9)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，尽管需要更多的调整，但是找到了合理的分组。

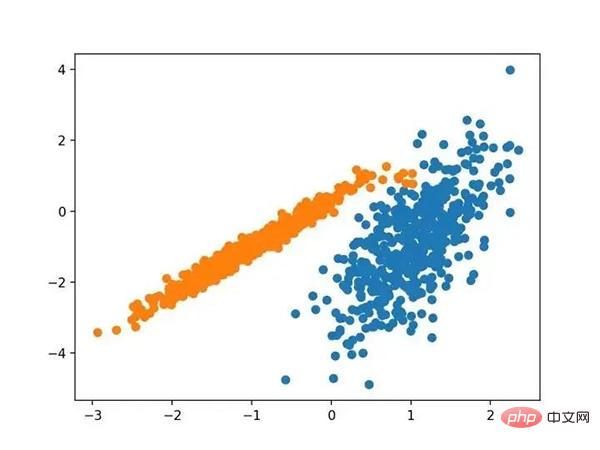
使用DBSCAN集群识别出具有集群的数据集的散点图

7.K均值

K-均值聚类可以是最常见的聚类算法，并涉及向群集分配示例，以尽量减少每个群集内的方差。

• 本文的主要目的是描述一种基于样本将 N 维种群划分为 k 个集合的过程。这个叫做“ K-均值”的过程似乎给出了在类内方差意义上相当有效的分区。
• -源自：《关于多元观测的分类和分析的一些方法》1967年

它是通过 K-均值类实现的，要优化的主要配置是“ n _ clusters ”超参数设置为数据中估计的群集数量。下面列出了完整的示例。

# k-means 聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = KMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以找到一个合理的分组，尽管每个维度中的不等等方差使得该方法不太适合该数据集。

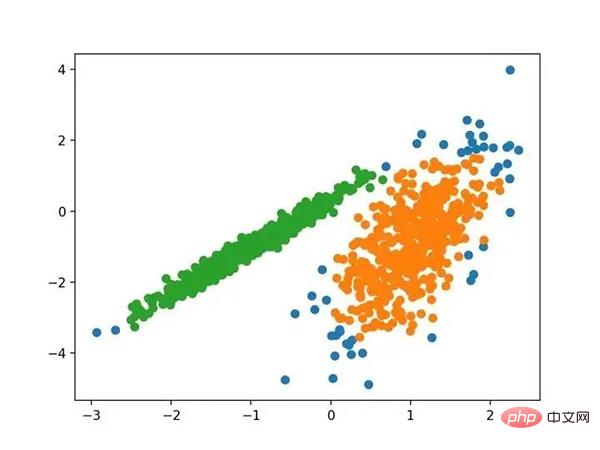
使用K均值聚类识别出具有聚类的数据集的散点图

8.Mini-Batch K-均值

Mini-Batch K-均值是 K-均值的修改版本，它使用小批量的样本而不是整个数据集对群集质心进行更新，这可以使大数据集的更新速度更快，并且可能对统计噪声更健壮。

• ...我们建议使用 k-均值聚类的迷你批量优化。与经典批处理算法相比，这降低了计算成本的数量级，同时提供了比在线随机梯度下降更好的解决方案。
• —源自：《Web-Scale K-均值聚类》2010

它是通过 MiniBatchKMeans 类实现的，要优化的主配置是“ n _ clusters ”超参数，设置为数据中估计的群集数量。下面列出了完整的示例。

# mini-batch k均值聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MiniBatchKMeans
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MiniBatchKMeans(n_clusters=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，会找到与标准 K-均值算法相当的结果。

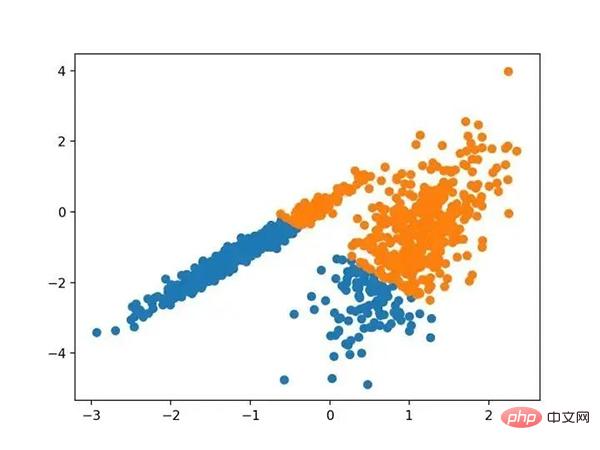
带有最小批次K均值聚类的聚类数据集的散点图

9.均值漂移聚类

均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。

• 对离散数据证明了递推平均移位程序收敛到最接近驻点的基础密度函数，从而证明了它在检测密度模式中的应用。
• —源自：《Mean Shift ：面向特征空间分析的稳健方法》，2002

它是通过 MeanShift 类实现的，主要配置是“带宽”超参数。下面列出了完整的示例。

# 均值漂移聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MeanShift
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = MeanShift()
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，可以在数据中找到一组合理的群集。

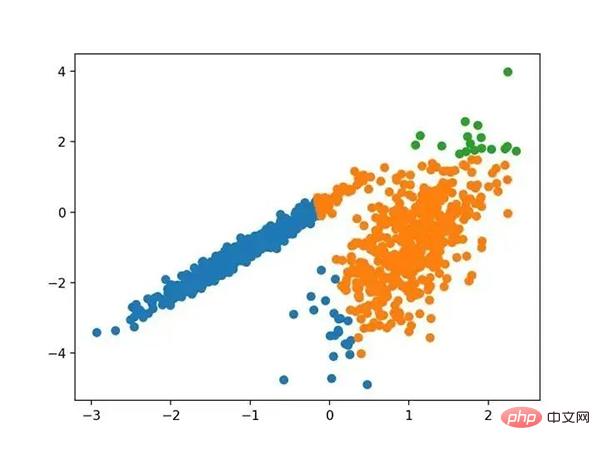
具有均值漂移聚类的聚类数据集散点图

10.OPTICS

OPTICS 聚类（ OPTICS 短于订购点数以标识聚类结构）是上述 DBSCAN 的修改版本。

• 我们为聚类分析引入了一种新的算法，它不会显式地生成一个数据集的聚类；而是创建表示其基于密度的聚类结构的数据库的增强排序。此群集排序包含相当于密度聚类的信息，该信息对应于范围广泛的参数设置。
• —源自：《OPTICS ：排序点以标识聚类结构》，1999

它是通过 OPTICS 类实现的，主要配置是“ eps ”和“ min _ samples ”超参数。下面列出了完整的示例。

# optics聚类
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import OPTICS
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = OPTICS(eps=0.8, min_samples=10)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，我无法在此数据集上获得合理的结果。

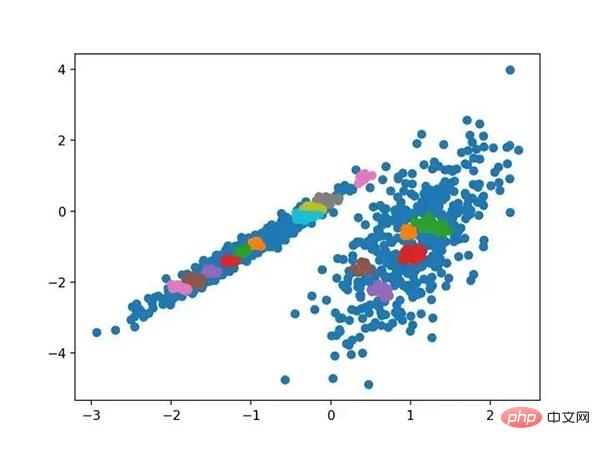
使用OPTICS聚类确定具有聚类的数据集的散点图

11.光谱聚类

光谱聚类是一类通用的聚类方法，取自线性线性代数。

• 最近在许多领域出现的一个有希望的替代方案是使用聚类的光谱方法。这里，使用从点之间的距离导出的矩阵的顶部特征向量。
• —源自：《关于光谱聚类：分析和算法》，2002年

它是通过 Spectral 聚类类实现的，而主要的 Spectral 聚类是一个由聚类方法组成的通用类，取自线性线性代数。要优化的是“ n _ clusters ”超参数，用于指定数据中的估计群集数量。下面列出了完整的示例。

# spectral clustering
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import SpectralClustering
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = SpectralClustering(n_clusters=2)
# 模型拟合与聚类预测
yhat = model.fit_predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。

在这种情况下，找到了合理的集群。

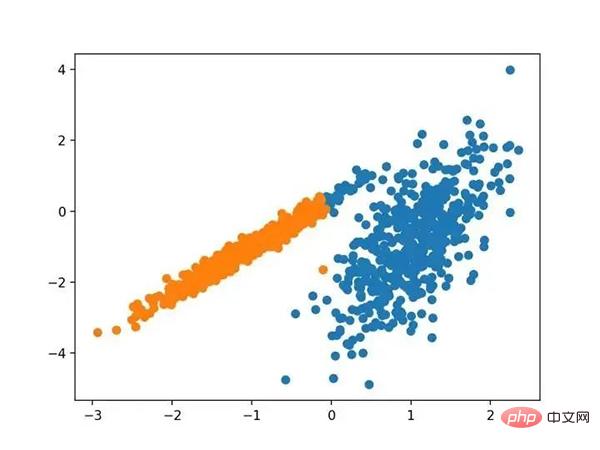
使用光谱聚类聚类识别出具有聚类的数据集的散点图

12.高斯混合模型

高斯混合模型总结了一个多变量概率密度函数，顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的，要优化的主要配置是“ n _ clusters ”超参数，用于指定数据中估计的群集数量。下面列出了完整的示例。

# 高斯混合模型
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot
# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
# 定义模型
model = GaussianMixture(n_components=2)
# 模型拟合
model.fit(X)
# 为每个示例分配一个集群
yhat = model.predict(X)
# 检索唯一群集
clusters = unique(yhat)
# 为每个群集的样本创建散点图
for cluster in clusters:
# 获取此群集的示例的行索引
row_ix = where(yhat == cluster)
# 创建这些样本的散布
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 绘制散点图
pyplot.show()

运行该示例符合训练数据集上的模型，并预测数据集中每个示例的群集。然后创建一个散点图，并由其指定的群集着色。在这种情况下，我们可以看到群集被完美地识别。这并不奇怪，因为数据集是作为 Gaussian 的混合生成的。

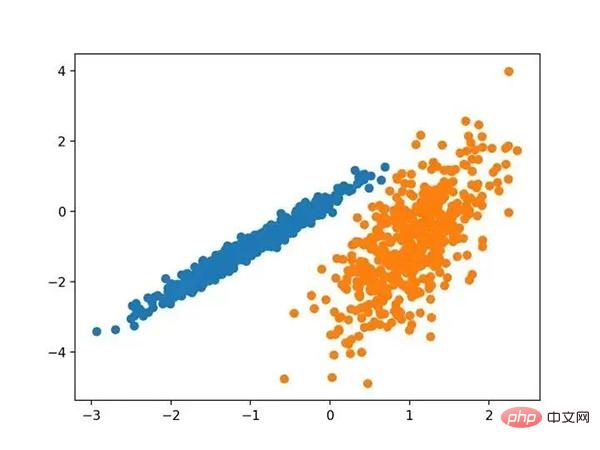
使用高斯混合聚类识别出具有聚类的数据集的散点图

三.总结

在本教程中，您发现了如何在 python 中安装和使用顶级聚类算法。具体来说，你学到了：

• 聚类是在特征空间输入数据中发现自然组的无监督问题。
• 有许多不同的聚类算法，对于所有数据集没有单一的最佳方法。
• 在 scikit-learn 机器学习库的 Python 中如何实现、适合和使用顶级聚类算法。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!