La théorie des graphes n’est en fait pas difficile à maîtriser

Pour les développeurs ayant de nombreuses années d'expérience en programmation, le concept de graphiques n'est pas étranger. De nombreuses grandes entreprises testent leur compréhension de la théorie des graphes lors d’entretiens techniques. En fait, les développeurs n’ont pas besoin de s’attaquer à des problèmes avancés pour tirer parti de ces concepts. Pour comprendre cela, nous pouvons d’abord examiner pourquoi les graphiques sont des structures de données populaires et comment les implémenter dans le code.

Modèle relationnel

Quelle que soit leur expérience en codage, les développeurs doivent avoir une certaine compréhension des types de données de tableau et de dictionnaire. Ces collections sont un concept standard utilisé dans la plupart des langues et fonctionnent bien lors de la présentation de contenu basé sur des listes :

La plupart du temps, les listes sont la solution parfaite pour afficher des informations à partir d'une base de données ou d'une requête basée sur REST. Cependant, les listes doivent parfois fournir des enregistrements ayant un contexte interdépendant. À ce stade, il devient pratique d’organiser les données sous forme de graphiques.

Avec les diagrammes, l'objectif principal n'est pas de lister des informations (même si cela peut être fait), mais de définir des relations entre les objets. Pourquoi est-il utile de définir des relations entre des objets ? Jetons un coup d'œil aux exemples suivants.

Un graphe non orienté avec deux sommets et une arête

(1) Application cartographique  :

Si on vous le demandait lors d'un entretien technique, comment organiseriez-vous les données afin qu'elles puissent être recréées Service de carte ( comme Apple ou Google Maps) ? En plus de fournir une liste de toutes les routes connues dans une base de données, le modèle que vous créez doit déterminer le meilleur moyen d'atteindre votre destination en fonction de facteurs tels que l'heure de la journée, le trafic et les rues à sens unique. Pour exploiter cette grande quantité de données, vous devez connaître la relation entre une route et toutes les autres rues du modèle.

(2) Médias sociaux  :

La valeur d'un média social est généralement mesurée par le nombre d'utilisateurs qui suivent ou suivent l'utilisateur. Les plateformes en ligne comme Twitter permettent aux utilisateurs de se connecter avec n'importe qui et de recevoir leurs dernières mises à jour, attirant ainsi un grand nombre d'utilisateurs.

Le modèle LinkedIn est plus détaillé car un utilisateur ne peut pas ajouter quelqu'un au réseau de cet utilisateur à moins que le destinataire n'accepte la demande de connexion de l'utilisateur. Dans ce cas, la connexion LinkedIn représente une relation bidirectionnelle. Dans le même esprit, les utilisateurs peuvent également rechercher sur leur réseau si quelqu'un est associé à l'opportunité d'emploi qu'ils souhaitent. Dans ce contexte, le terme « réseau » peut désigner des connexions directes ou indirectes. Un modèle aussi puissant ne repose pas uniquement sur une simple liste, il contient l’intelligence nécessaire pour déterminer comment tous les profils sont liés.

Composants graphiques

Maintenant que nous comprenons comment les graphiques sont utilisés dans les applications quotidiennes, introduisons les composants des graphiques.

Les nœuds du graphique sont appelés sommets. Bien que les graphiques puissent être construits sous forme de sommets uniques, les modèles contenant plusieurs sommets représentent mieux les applications du monde réel.

Les objets d'un graphique sont liés les uns aux autres via des connexions appelées arêtes.

Selon vos besoins, un sommet peut être connecté à un ou plusieurs objets via des arêtes, ou vous pouvez créer un sommet sans arêtes.

Enfin, contrairement à d'autres structures standards telles que les piles ou les files d'attente, les graphiques n'ont généralement pas de point de début ou de fin spécifié. Voici quelques exemples de configurations de graphes :

Un graphe non orienté avec deux sommets et une arête

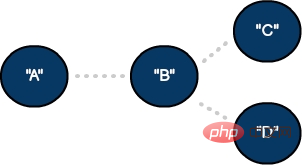
Un graphe non orienté avec deux sommets et une arête

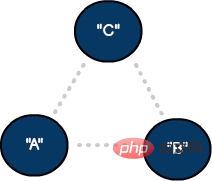
Un graphe non orienté avec deux sommets et une arête

Orienté et non orienté

Dans un graphe non orienté, les connexions entre les sommets sources et les cibles sont égal. Ces modèles représentent des connexions bidirectionnelles, similaires aux rues à double sens dans les applications cartographiques.

Pour définir une connexion unidirectionnelle, nous pouvons mettre à jour le modèle vers un graphe orienté à l'aide de lignes et de flèches :

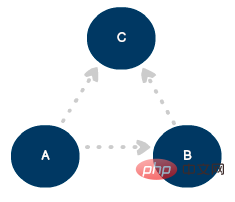
Graphique orienté avec trois sommets et trois arêtes

Niveau de connectivité

Parfois, nous doivent représenter le degré de connectivité entre les sommets dans un graphique. Cette technique fonctionne bien pour quantifier la distance, le temps ou la gravité entre les nœuds. Le poids est généralement associé à un bord et est une variable de comparaison utilisée pour le suivi. .

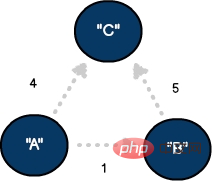
Graphique orienté avec trois sommets et trois arêtes, où les arêtes sont pondérées

Vertices du graphique

Avec une compréhension de base de la théorie des graphes, voyons comment le faire dans le code Copiez ces modèles. Ci-dessous, nous créons un sommet qui prend en charge un objet générique personnalisé (T). Une variable tvalue représente les données détenues par ce type, y compris une chaîne unique, un entier ou un type personnalisé (par exemple, un nom de rue ou un profil de réseau social).

Assurez-vous également que notre type est conforme au protocole Equatable (Swift) populaire. Cela nous permet de comparer des instances de sommets spécifiques pour l'égalité lorsque cela est nécessaire.

public class Vertex <t> : Equatable {<br><br>​var tvalue: T?<br>​var neighbors = Array<edge>>()<br>​let uuid = UUID()<br><br>​public init(with name: T) {<br>self.tvalue = name<br>​}<br><br>​//equatable conformance<br>​public static func == (lhs: Vertex, rhs: Vertex) -> Bool {<br> return lhs.uuid == rhs.uuid<br>​}<br>}</edge></t>

Liste d'adjacence

La liste d'adjacence représente la connexion avec d'autres sommets. Comme mentionné précédemment, chaque sommet peut être connecté à un ou plusieurs sommets adjacents. Cette liste de relations est parfois appelée « liste de contiguïté » et peut être utilisée pour résoudre de nombreux problèmes avancés.

var neighbors = Array<edge>>()</edge>

Graph Edges

Lors de la création d'un sommet, nous avons ajouté une propriété de contiguïté pour stocker un tableau de types d'arêtes personnalisés. Le bord inférieur fournit une référence pour les sommets adjacents suivants et leurs poids de bord potentiels.

public class Edge <t> {<br><br>​var neighbor: Vertex<t><br>​var weight: Int<br><br>​init() {<br> weight = 0<br> self.neighbor = Vertex<t>()<br>​}<br>}</t></t></t>

Construire le canevas

Avec les objets sommet et bord en main, nous pouvons maintenant les ajouter à la structure de stockage centrale que nous appelons le canevas graphique. Bien que notre toile soit techniquement un tableau, notre objectif est de visualiser la collection comme un ensemble de relations. Avec la fonction addVertex, nous pouvons ajouter un seul sommet générique au canevas, tandis que la méthode addEdge fournit les informations de référence nécessaires pour le bord.

Enfin, notre code suppose que le graphe est orienté, puisque les arêtes sont (uniquement) ajoutées à la liste de contiguïté des sommets source.

public class Graph <t> {<br><br>​var canvas: Array<vertex>><br><br> public init() {<br> canvas = Array<vertex>()<br>​}<br><br>​//add vertex to graph canvas<br>​public func addVertex(element: Vertex<t>) {<br> canvas.append(element)<br>​}<br>/add edge<br>​public func addEdge(source: Vertex<t>, neighbor: Vertex<t>, weight: Int) {<br><br> //create a new edge<br> let newEdge = Edge<t>()<br><br> //connect source vertex to neighboring edge<br> newEdge.neighbor = neighbor<br> newEdge.weight = weight<br><br> source.neighbors.append(newEdge)<br>​}<br>}</t></t></t></t></vertex></vertex></t>

En résumé, nous vous avons présenté les graphiques et vu comment ils peuvent être utilisés pour représenter les relations entre les objets. Nous avons également examiné plusieurs façons de configurer les graphiques et les composants utilisés pour décrire différents modèles.

Une fois le modèle défini, nous posons les bases de fonctionnalités plus avancées, notamment des algorithmes de navigation graphique et de parcours tels que la recherche en largeur d'abord.

Présentation du traducteur

Kang Shaojing, rédacteur en chef de la communauté 51CTO, est actuellement engagé dans le secteur des communications, occupant des postes de développement de pilotes de bas niveau. Il a étudié les structures de données, Python et s'intéresse maintenant aux systèmes d'exploitation, aux bases de données et à d'autres domaines connexes. champs.

Titre original : Le guide complet du débutant sur la théorie des graphes, auteur : Wayne Bishop

Lien :

https://stackoverflow.blog/2022/05/26/the-complete-beginners-guide-to-graph-theory /

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!