Les systèmes d'apprentissage automatique modulaires sont-ils suffisants ? Les professeurs et les étudiants de Bengio vous donnent la réponse

Les chercheurs en apprentissage profond s'inspirent des neurosciences et des sciences cognitives. Depuis les unités cachées et les méthodes de saisie jusqu'à la conception de connexions et d'architectures de réseau, de nombreuses études révolutionnaires sont basées sur l'imitation de stratégies de fonctionnement du cerveau. Il ne fait aucun doute que la modularité et l’attention ont été fréquemment utilisées en combinaison dans les réseaux artificiels ces dernières années et ont donné des résultats impressionnants.

En fait, la recherche en neurosciences cognitives montre que le cortex cérébral représente la connaissance de manière modulaire, communique entre différents modules et que le mécanisme d'attention effectue la sélection du contenu. C'est la modularité et l'attention mentionnées ci-dessus. Dans des recherches récentes, il a été suggéré que ce mode de communication dans le cerveau pourrait avoir des implications en matière de biais inductifs dans les réseaux profonds. La rareté des dépendances entre ces variables de haut niveau décompose les connaissances en fragments recombinables aussi indépendants que possible, rendant l’apprentissage plus efficace.

Bien que de nombreuses recherches récentes reposent sur de telles architectures modulaires, les chercheurs utilisent un grand nombre d'astuces et de modifications architecturales, ce qui rend difficile l'analyse de principes architecturaux réels et utilisables.

Les systèmes d'apprentissage automatique montrent progressivement les avantages des architectures plus clairsemées et plus modulaires. Les architectures modulaires ont non seulement de bonnes performances de généralisation, mais apportent également de meilleures performances et évolutivité hors distribution (OoD). interprétabilité. L’une des clés du succès de tels systèmes réside dans le fait que les systèmes de génération de données utilisés dans des contextes réels sont considérés comme constitués de parties peu interagissantes, et il serait utile de donner au modèle un biais inductif similaire. Cependant, étant donné que la distribution de ces données du monde réel est complexe et inconnue, le domaine manque d’évaluation quantitative rigoureuse de ces systèmes.

Un article rédigé par trois chercheurs de l'Université de Montréal au Canada : Sarthak Mittal, Yoshua Bengio et Guillaume Lajoie. Ils ont mené une évaluation complète des architectures modulaires courantes grâce à une distribution de données modulaire simple et connue. L'étude met en évidence les avantages de la modularité et de la parcimonie et révèle un aperçu des défis rencontrés lors de l'optimisation des systèmes modulaires. Le premier auteur et auteur correspondant, Sarthak Mittal, est un élève en master de Bengio et Lajoie.

• Adresse papier : https://arxiv.org/pdf/2206.02713.pdf
• Adresse GitHub : https://github.com/sarthmit/Mod_Arch

Plus précisément, ceci L'étude étend l'analyse de Rosenbaum et al. et propose une méthode pour évaluer, quantifier et analyser les composants communs des architectures modulaires. À cette fin, la recherche a développé une série de références et de mesures conçues pour explorer l’efficacité des réseaux modulaires. Cela révèle des informations précieuses qui aident à identifier non seulement où les approches actuelles réussissent, mais également quand et comment ces approches échouent.

La contribution de cette recherche peut être résumée comme suit :

• Cette recherche développe des tâches et des métriques de référence basées sur des règles de sélection probabilistes, et utilise des références et des métriques pour quantifier deux phénomènes importants dans les systèmes modulaires : l'effondrement et la spécialisation.
• Cette étude extrait les biais inductifs modulaires couramment utilisés et les évalue systématiquement à travers une série de modèles conçus pour extraire les propriétés architecturales couramment utilisées (modèles monolithiques, modulaires, modulaires-op, GT-Modulaires).
• L'étude a révélé que la spécialisation dans les systèmes modulaires peut améliorer considérablement les performances du modèle lorsqu'il existe de nombreuses règles latentes dans une tâche, mais pas lorsqu'il n'y en a que quelques-unes.
• L'étude a révélé que les systèmes modulaires standards ont tendance à être sous-optimaux, à la fois dans leur capacité à se concentrer sur les bonnes informations et dans leur capacité à se spécialiser, ce qui suggère la nécessité d'un biais inductif supplémentaire.

Définition / Terminologie

Dans cet article, nous explorons comment une série de systèmes modulaires effectuent des tâches communes formulées par un processus de génération de données synthétiques que nous appelons données de règles. Ils présentent la définition des composants clés, notamment (1) les règles et la manière dont ces règles forment des tâches, (2) les modules et la manière dont ces modules adoptent différentes architectures de modèles, (3) la spécialisation et la manière dont les modèles sont évalués. Les paramètres détaillés sont présentés dans la figure 1 ci-dessous.

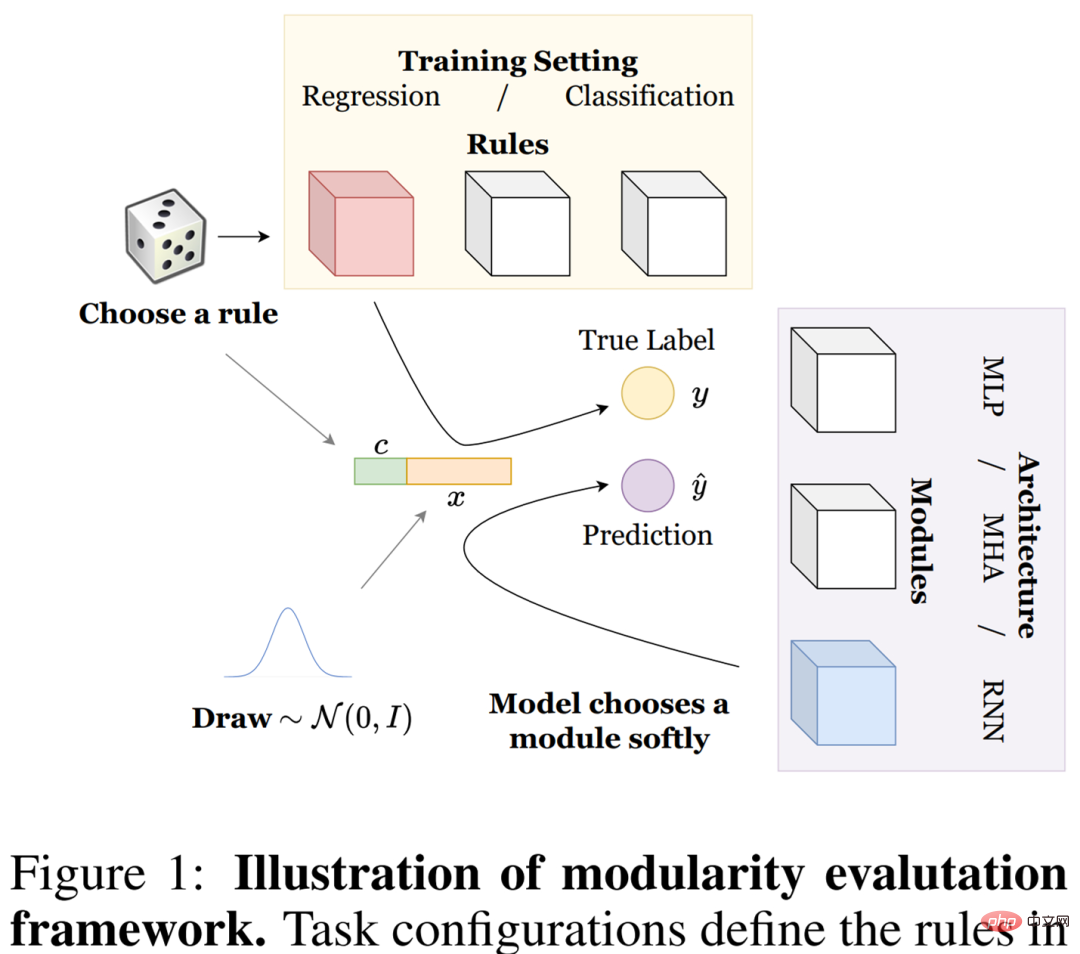
Règles. Afin de bien comprendre les systèmes modulaires et d'analyser leurs avantages et leurs inconvénients, les chercheurs ont envisagé une configuration complète permettant un contrôle précis des différentes exigences des tâches. En particulier, les opérations, qu'ils appellent règles, doivent être apprises sur les distributions génératrices de données présentées dans l'équation 1-3 ci-dessous.

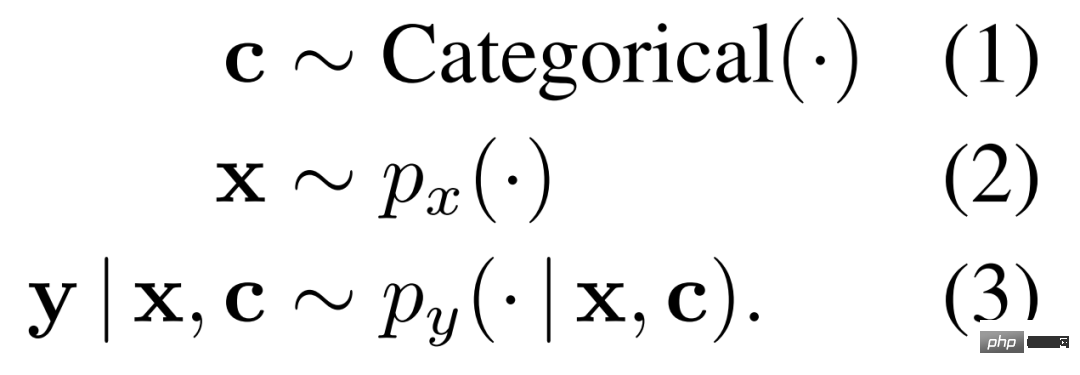
Étant donné la distribution ci-dessus, le chercheur définit une règle pour devenir son expert, c'est-à-dire que la règle r est définie comme p_y(·|x, c = r), où c est la classification représentant la variable de contexte, x est la séquence d'entrée.

Mission. Une tâche est décrite par un ensemble de règles (distributions génératrices de données) présentées dans l'équation 1-3. Différents ensembles de {p_y(· | x, c)}_c signifient différentes tâches. Pour un nombre donné de règles, le modèle est entraîné sur plusieurs tâches afin d'éliminer tout biais spécifique à la tâche.

module. Un système modulaire se compose d'un ensemble de modules de réseau neuronal, où chaque module contribue au résultat global. Cela peut être vu à travers la forme fonctionnelle suivante.

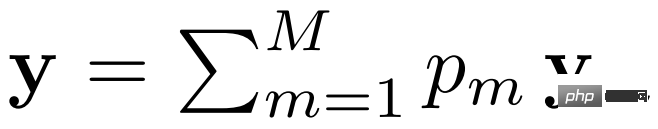
où y_m représente la sortie et p_m représente l'activation du m^ième module.

Architecture modèle. L'architecture modèle décrit quelle architecture est choisie pour chaque module d'un système modulaire ou pour les modules individuels d'un système monolithique. Dans cet article, les chercheurs envisagent d’utiliser le perceptron multicouche (MLP), l’attention multi-têtes (MHA) et le réseau neuronal récurrent (RNN). Il est important que les règles (ou distributions génératrices de données) soient adaptées à l'architecture du modèle, comme les règles basées sur MLP.

Processus de génération de données

Étant donné que les chercheurs visent à explorer les systèmes modulaires à l'aide de données synthétiques, ils détaillent le processus de génération de données basé sur le schéma de règles décrit ci-dessus. Plus précisément, les chercheurs ont utilisé un simple processus de génération de données de type mixte d'experts (MoE), dans l'espoir que différents modules pourraient être spécialisés pour différents experts en règles.

Ils expliquent le processus de génération de données pour trois architectures de modèles, qui sont MLP, MHA et RNN. De plus, il existe deux versions sous chaque tâche : régression et classification.

MLP. Les chercheurs ont défini un schéma de données adapté à l'apprentissage basé sur des systèmes MLP modulaires. Dans ce schéma de génération de données synthétiques, un échantillon de données se compose de deux nombres indépendants et d'une sélection régulière échantillonnée à partir d'une certaine distribution. Différentes règles génèrent différentes combinaisons linéaires de deux nombres pour donner un résultat, c'est-à-dire que la sélection de la combinaison linéaire est instanciée dynamiquement selon les règles, comme le montre l'équation 4-6 ci-dessous.

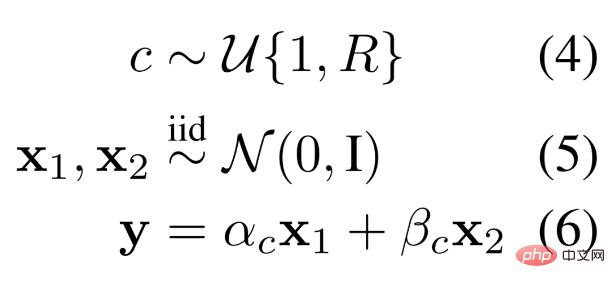
MHA. Aujourd’hui, les chercheurs ont défini un schéma de données adapté à l’apprentissage dans un système MHA modulaire. Par conséquent, ils ont conçu une distribution de génération de données avec la propriété suivante : chaque règle se compose de différents concepts de recherche, de récupération et de la combinaison linéaire finale des informations récupérées. Les chercheurs décrivent mathématiquement ce processus dans l’équation 7-11 ci-dessous.

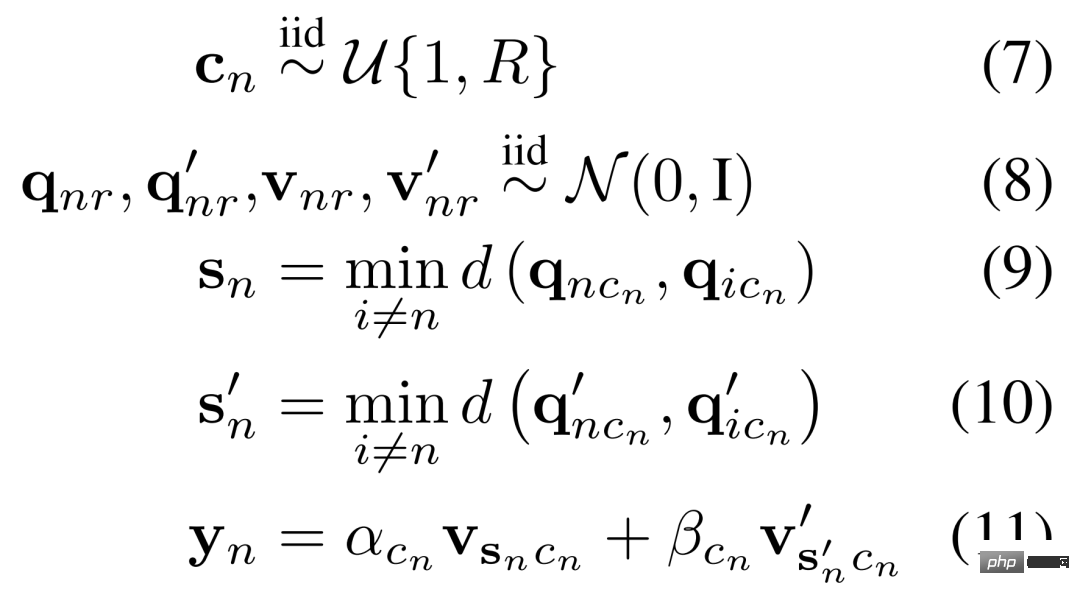
RNN. Pour les systèmes circulatoires, les chercheurs ont défini des règles pour un système dynamique linéaire dans lequel l'une des multiples règles peut être déclenchée à tout moment. Mathématiquement, ce processus est illustré dans l'équation 12-15 ci-dessous.

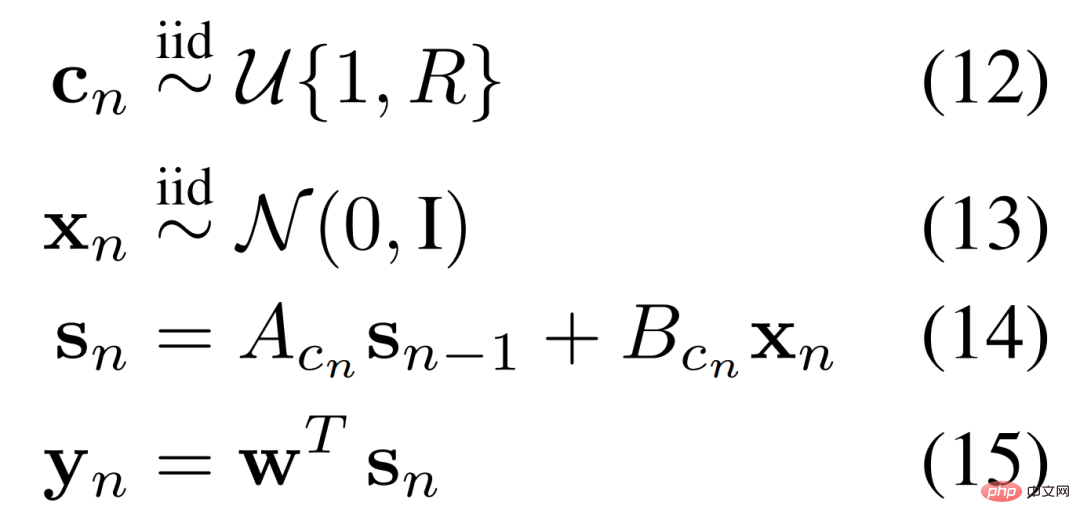
Modèle

Certains travaux antérieurs affirmaient que les systèmes de modules formés de bout en bout sont supérieurs aux systèmes monolithiques, en particulier dans les environnements distribués. Cependant, il n'y a pas eu d'analyse détaillée et approfondie des avantages de ces systèmes modulaires ni de leur spécialisation réelle en fonction de la distribution de la génération de données.

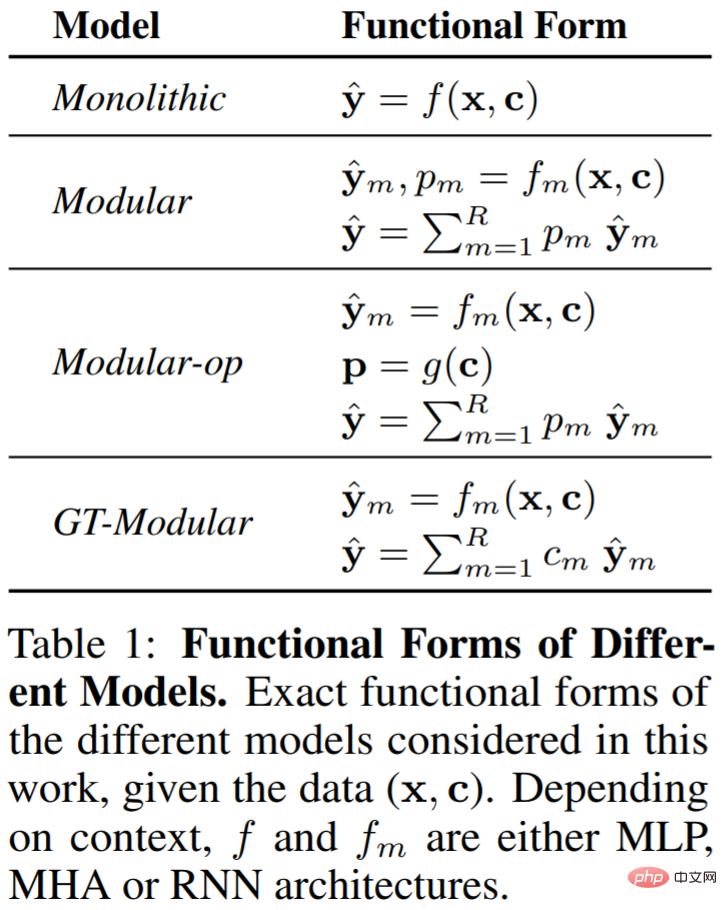
Par conséquent, les chercheurs ont considéré quatre types de modèles qui permettent différents degrés de spécialisation, à savoir Monolithique (unique), Modulaire (modulaire), Modulaire-op et GT-Modulaire. Le tableau 1 ci-dessous illustre ces modèles.

Monolithique. Un système monolithique est un grand réseau de neurones qui prend en entrée tout un ensemble de données (x, c) et fait une prédiction y^ sur cette base. Il n'y a aucun biais inductif en faveur de la modularité ou de la rareté de l'explicite intégré au système, et il repose entièrement sur la rétropropagation pour apprendre la forme fonctionnelle requise pour résoudre la tâche.

Modulaire. Un système modulaire se compose de nombreux modules, chacun étant un réseau neuronal d'un type d'architecture donné (MLP, MHA ou RNN). Chaque module m prend les données (x, c) en entrée et calcule une sortie yˆ_m et un score de confiance, normalisé entre les modules à la probabilité d'activation p_m.

Opération modulaire. Un système d'exploitation modulaire est très similaire à un système modulaire, avec une différence. Au lieu de définir la probabilité d'activation p_m du module m en fonction de (x, c), les chercheurs ont veillé à ce que l'activation soit déterminée uniquement par le contexte de règle C.

GT-Modulaire. Les systèmes modulaires à valeur réelle servent de références oracle, c'est-à-dire des systèmes modulaires parfaitement spécialisés.

Les chercheurs montrent que du monolithique au GT-Modulaire, les modèles incluent de plus en plus de biais inductifs pour la modularité et la parcimonie.

Metrics

Pour évaluer de manière fiable les systèmes modulaires, les chercheurs ont proposé une série de mesures qui non seulement mesurent les avantages en termes de performances de tels systèmes, mais les évaluent également sous deux formes importantes : l'effondrement et la spécialisation.

Performances. Le premier ensemble de mesures d'évaluation est basé sur les performances dans les contextes de distribution et hors distribution (OoD), reflétant les performances de différents modèles sur diverses tâches. Pour le paramètre de classification, nous rapportons l'erreur de classification ; pour le paramètre de régression, nous rapportons la perte.

Crash. Les chercheurs ont proposé un ensemble de mesures, Collapse-Avg et Collapse-Worst, pour quantifier le degré d'effondrement rencontré par un système modulaire (c'est-à-dire le degré de sous-utilisation des modules). La figure 2 ci-dessous montre un exemple où vous pouvez voir que le module 3 n'est pas utilisé.

Professionnalisation. Pour compléter les métriques d'effondrement, nous proposons également l'ensemble de métriques suivant, à savoir (1) l'alignement, (2) l'adaptation et (3) l'information mutuelle inverse qui quantifie le degré de spécialisation atteint par un système modulaire.

Expériences

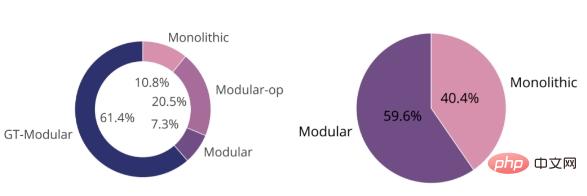
La figure ci-dessous montre que le système GT-Modular est optimal dans la plupart des cas (à gauche), ce qui montre que la spécialisation est bénéfique. Nous constatons également qu'entre le système modulaire standard formé de bout en bout et le système monolithique, le premier surpasse le second, mais pas de beaucoup. Ensemble, ces deux diagrammes circulaires démontrent que les systèmes modulaires actuels pour une formation de bout en bout ne permettent pas une bonne spécialisation et sont donc largement sous-optimaux.

L'étude examine ensuite des choix d'architecture spécifiques et analyse leurs performances et leurs tendances à travers un nombre croissant de règles.

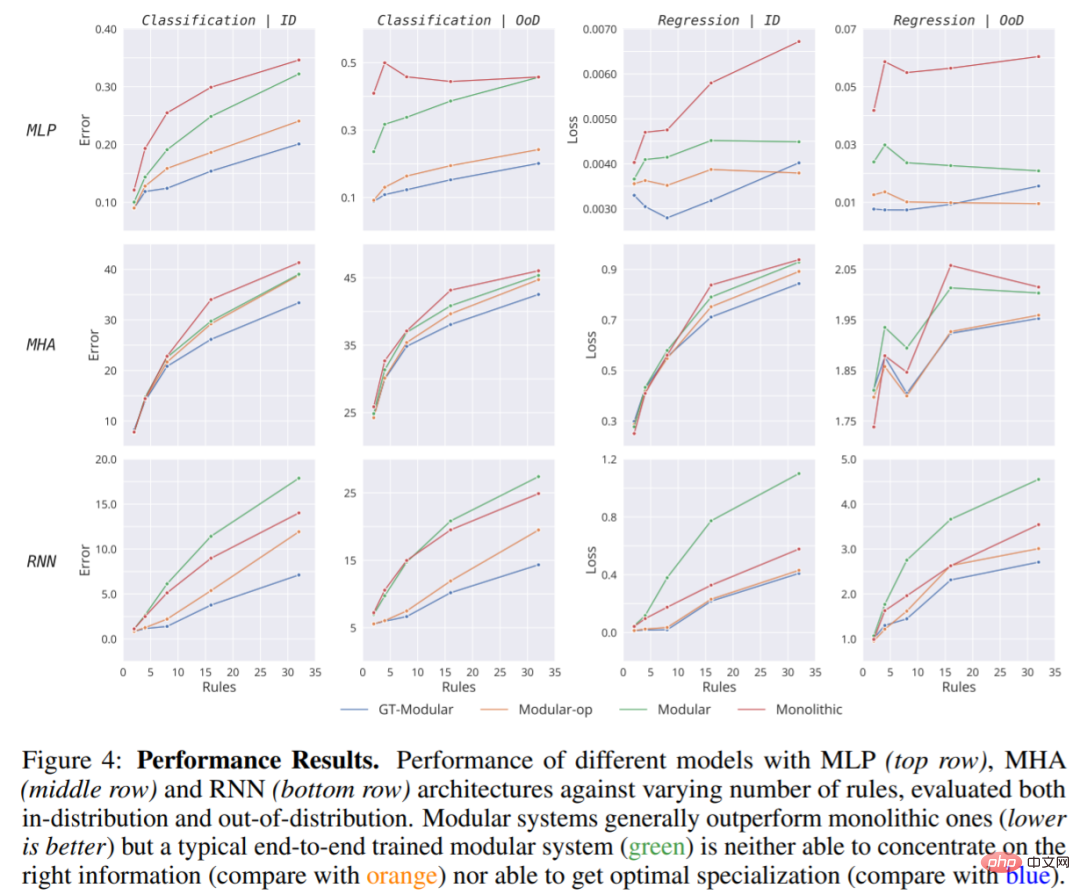
La figure 4 montre que même si un système parfaitement spécialisé (GT-Modular) apporterait des avantages, un système modulaire typique pour une formation de bout en bout est sous-optimal et ne peut pas offrir ces avantages, d'autant plus que le nombre de règles augmente. De plus, même si ces systèmes modulaires de bout en bout surpassent souvent les systèmes monolithiques, l’avantage n’est généralement que minime.

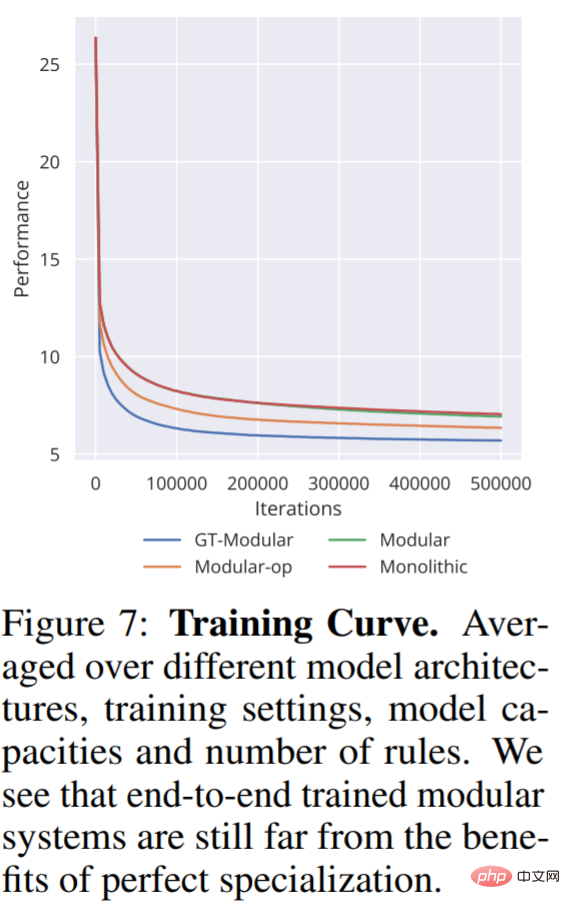
Dans la figure 7, nous voyons également la moyenne des modes d'entraînement pour différents modèles sur tous les autres paramètres, la moyenne inclut l'erreur de classification et la perte de régression. Comme on peut le constater, une bonne spécialisation conduit non seulement à de meilleures performances, mais accélère également la formation.

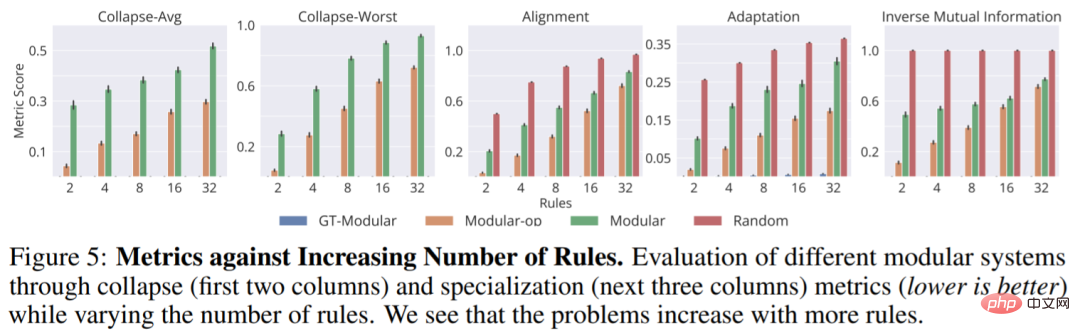
La figure suivante montre deux mesures d'effondrement : Collapse-Avg et Collapse-Worst. De plus, la figure ci-dessous montre également trois indicateurs de spécialisation, d'alignement, d'adaptation et d'information mutuelle inverse pour différents modèles avec différents nombres de règles :

​

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!