Ne réfléchissez pas étape par étape ! Le dernier algorithme de raisonnement en langage naturel de Google, LAMBADA : le « raisonnement en chaîne inversée » est la réponse

​Le raisonnement automatique est définitivement un gros problème dans le domaine du traitement du langage naturel. Le modèle doit tirer des conclusions efficaces et correctes basées sur des prémisses et des connaissances données.

Bien que le domaine de la PNL ait atteint des performances extrêmement élevées dans diverses tâches de « compréhension du langage naturel » telles que la compréhension écrite et la réponse aux questions grâce à des modèles linguistiques pré-entraînés à grande échelle au cours des dernières années, les performances de ces modèles en matière de raisonnement logique est encore très en retard.

Chain of Thought (CoT) est sorti en mai de l'année dernière. Certains chercheurs ont découvert que le simple fait d'ajouter « Pensons étape par étape » à l'invite peut améliorer considérablement les performances d'inférence de GPT-3, par exemple. MultiArith, la précision de l'inférence est passée des 17,7 % précédents à 78,7 %

Mais des méthodes telles que CoT et Selection Inference recherchent toutes à partir d'axiomes dans le sens direct. Le processus de preuve (preuve) pour dériver la conclusion finale (conclusion) a. le problème de l'explosion combinatoire de l'espace de recherche, donc pour des chaînes de raisonnement plus longues, le taux d'échec est plus élevé.

Récemment, Google Research a développé un algorithme de chaînage arrière LAMBADA (LANguage Model augmenté BACKwarD chaining), qui combine "l'efficacité du raisonnement en arrière est nettement supérieure à celle du raisonnement en avant" dérivée de la littérature de raisonnement classique. Une conclusion est appliquée au modèle de langage. (LM).

Lien papier : https://arxiv.org/abs/2212.13894

LAMBADA décompose le processus de raisonnement en quatre sous-modules, chaque module est implémenté par un raisonnement sur un modèle de langage invité en quelques étapes.

En fin de compte, LAMBADA a obtenu des améliorations significatives des performances sur les deux ensembles de données de raisonnement logique par rapport à la méthode de raisonnement avancé actuelle de sota. Surtout lorsque le problème nécessite une chaîne de preuve approfondie et précise, l'amélioration des performances de LAMBADA est encore plus évidente. .

Le « raisonnement inversé » devient la réponse ?

Le raisonnement logique, en particulier le raisonnement logique sur un texte naturel non structuré, est l'élément de base de la découverte automatique des connaissances et la clé des progrès futurs dans divers domaines scientifiques.

Bien que le développement de nombreuses tâches PNL ait bénéficié de l'échelle croissante des modèles de langage pré-entraînés, il a été observé que l'augmentation de la taille du modèle n'a apporté qu'une amélioration très limitée dans la résolution de problèmes de raisonnement complexes.

Dans la littérature classique, il existe deux principales méthodes de raisonnement logique :

1 Le Forward Chaining (FC), c'est-à-dire partir de faits et de règles, faire de nouvelles inférences et les ajouter entre les théories et itérer jusqu'à l'objectif. la déclaration peut être prouvée ou réfutée 

2. Le chaînage arrière (BC), c'est-à-dire qu'en partant de l'objectif, le décomposer de manière récursive en sous-objectifs jusqu'à ce que les sous-objectifs puissent être prouvés ou réfutés sur la base de faits.

Les méthodes de raisonnement précédentes utilisant des modèles de langage adoptaient pour la plupart l'idée du raisonnement en chaîne avant, qui nécessite de sélectionner un sous-ensemble de faits et de règles dans l'ensemble. Cela peut être difficile pour LM car cela nécessite une recherche combinatoire dans. un grand espace.

De plus, décider quand arrêter la recherche et déclarer la preuve échouée est également très difficile en FC, nécessitant parfois même un module spécifiquement formé sur les étiquettes intermédiaires.

En fait, la littérature classique sur le raisonnement automatique se concentre en grande partie sur le raisonnement en chaîne arrière ou sur les stratégies de vérification orientées vers un objectif.

LAMBADA

LAMBADA signifie "modèle de langage amélioré par la technologie de chaînage inverse". Les chercheurs ont prouvé expérimentalement que BC est plus adapté au raisonnement logique déductif basé sur du texte.

BC ne nécessite pas un grand nombre de recherches combinatoires pour sélectionner des sous-ensembles et dispose de critères d'arrêt plus naturels.

LAMBADA se concentre principalement sur le raisonnement automatique sur les faits, c'est-à-dire les assertions en langage naturel, telles que "Les bonnes personnes sont rouges". Ces assertions sont cohérentes mais pas nécessairement basées sur la situation réelle.

Une règle est écrite par une déclaration en langage naturel, qui peut être réécrite sous la forme "si P alors Q". Par exemple, "Les gens durs et gentils sont rouges" peut être réécrit comme "si une personne est dure". " Si une personne est dure et gentille, alors elle est rouge.

où P est appelé l'antécédent de la règle, et Q est appelé le conséquent de la règle.

Une théorie C se compose de faits F={f1, f2, , fn} et de règles R={r1, r2, rm}. objectif de faits et de règles.

Exemple 1, un exemple théorique C avec des personnages fictifs et des règles

F={"Fiona est une bonne personne", "Fiona est une personne dure"}

R={"Si quelqu'un Si une personne est intelligent, alors c'est une bonne personne", "Une bonne personne rude est rouge", "Être une bonne personne et rouge signifie qu'il est rond"}.

Sur la base de la théorie ci-dessus, on pourrait vouloir prouver ou réfuter un objectif, tel que « Fiona est rouge ?

Raisonnement par chaînage arrière

Le fait qu'une règle s'applique à un objectif est déterminé par une opération appelée unification en logique.

Par exemple, pour le but « Fiona est rouge ? » dans l'exemple 1, la deuxième règle a les mêmes conséquences que le but, elle peut donc être appliquée mais les deux autres règles ont des conséquences différentes, donc elles ne le font pas ; Je ne m'applique pas.

Considérant la théorie et les objectifs de l'exemple 1, BC commence à raisonner à partir de l'objectif « Fiona est rouge ?

Tout d'abord, BC vérifie si l'objectif peut être prouvé ou infirmé à partir de faits. Puisqu'il n'y a aucun fait pour prouver ou réfuter cet objectif, nous vérifions ensuite si cet objectif est cohérent avec les résultats de certaines règles, et nous constatons qu'il est cohérent avec la deuxième règle « Les gens durs et bons sont rouges ».

Cet objectif peut donc être décomposé en deux sous-objectifs : 1) Fiona est-elle dure ? et 2) Fiona est-elle une bonne personne ? .

Étant donné que les deux sous-objectifs peuvent être prouvés à partir de faits, BC conclut que l'objectif initial peut être prouvé.

Pour un objectif, le résultat de BC est soit une preuve, un déni, ou un inconnu (par exemple, l'objectif "Fiona est intelligente ?").

Modèle linguistique dans LAMBADA

Afin d'utiliser BC pour le raisonnement basé sur du texte, les chercheurs ont introduit quatre modules basés sur LM : vérification des faits, sélection de règles, décomposition des objectifs) et accord de signature.

Vérification des faits

Étant donné un ensemble de faits F et un objectif G dans la théorie, le module de vérification des faits vérifie s'il existe un fait f∈F tel que f contient G ( ici Dans ce cas, le but est prouvé) ou f contient la négation de G (auquel cas le but est nié).

Si un tel fait ne peut être trouvé, alors la vérité de G reste inconnue.

La mise en œuvre de la vérification des faits comprend deux sous-modules : le premier sous-module sélectionne un fait parmi l'ensemble des faits les plus pertinents pour l'objectif, et le deuxième sous-module vérifie si l'objectif peut être prouvé ou réfuté en fonction de l'objectif. sur ce fait.

Étant donné que le sous-module de sélection des faits peut ne pas déterminer les meilleurs faits du premier coup, si la vérité de la cible est toujours inconnue après un appel au sous-module, les faits sélectionnés peuvent être supprimés et le sous-module -module est appelé à nouveau ; ce processus peut être répété plusieurs fois.

Sélection de règles

Étant donné un ensemble de règles R et un objectif G dans la théorie, le module de sélection de règles détermine la règle r∈R pour rendre le résultat de r cohérent avec G, puis utilise celles-ci règles pour fixer l'objectif. Décomposez-le en sous-objectifs.

Si de telles règles ne peuvent pas être déterminées, alors la vérité de G reste inconnue.

La sélection des règles comprend également deux sous-modules : le premier sous-module détermine le résultat de chaque règle (indépendant de l'objectif), et le deuxième sous-module prend le résultat et l'objectif de la règle en entrée et détermine lequel on est conforme au but.

Il convient de noter qu'en raison de la nature récursive de BC, le module de sélection de règles peut être appelé plusieurs fois dans le processus de preuve d'un objectif. Le résultat de l’identification de chaque règle étant indépendant de la cible, ce sous-module ne doit être appelé qu’une seule fois.

Décomposition des objectifs

Étant donné une règle r et un objectif G tels que le résultat de r soit unifié avec G, le module de décomposition des objectifs détermine les sous-objectifs qui doivent être prouvés pour que G soit prouvé ou réfuté.

Dans le cas d'une preuve réussie de l'antécédent de r, le fait que la cible soit prouvée ou réfutée dépend de la cohérence du signe de la cible avec le signe du résultat de r.

Par exemple, pour le but "Fiona est rouge ?", puisque le signe du but est cohérent avec le signe résultat de la deuxième règle, et que l'antécédent de la règle est prouvé, on peut conclure que le but est prouvé.

Cohérence symbolique

Étant donné une règle r et un objectif G, le module de cohérence symbolique vérifie si le signe résultant de r est cohérent ou incohérent avec le signe du but.

Partie expérimentale

Les chercheurs ont choisi Chain of Thought (CoT), la méthode de raisonnement neuronal sota basée sur un raisonnement explicite, et la méthode de raisonnement du module sota Selection Inference (SI) comme modèle de base pour la comparaison.

Les ensembles de données expérimentaux utilisent ProofWriter et PrOntoQA. Ces ensembles de données sont difficiles pour l'inférence LM et contiennent des exemples dans lesquels des longueurs de chaîne allant jusqu'à 5 sauts doivent être prouvées, ainsi que des exemples dans lesquels la cible ne peut être ni prouvée ni réfutée. la théorie proposée.

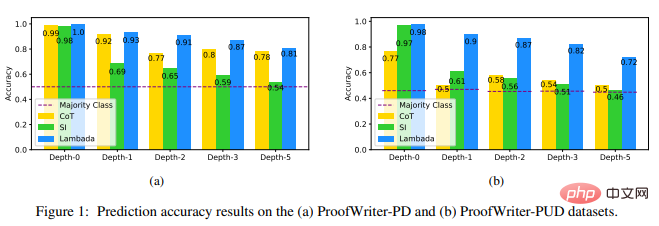
Les résultats expérimentaux montrent que LAMBADA surpasse considérablement les deux autres lignes de base, en particulier sur l'ensemble de données ProofWriter-PUD contenant des étiquettes INCONNUES (amélioration relative de 44 % par rapport à CoT et 56 % par rapport au SI à une profondeur d'amélioration de 5 %), et aux profondeurs plus élevées. de PrOntoQA (amélioration relative de 37 % par rapport au CoT et amélioration relative de 113 % par rapport au SI à la profondeur -5).

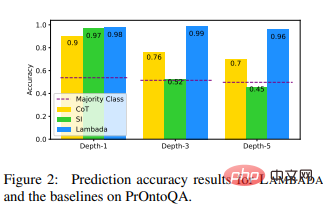
Ces résultats montrent les avantages de LAMBADA dans le raisonnement logique et montrent également que le chaînage vers l'arrière (qui est l'épine dorsale du raisonnement dans LAMBADA) est possible par rapport au chaînage vers l'avant (qui est l'épine dorsale du SI) est un meilleur choix.

Ces résultats révèlent également une faille dans la méthode CoT lorsqu'il s'agit d'étiquettes INCONNUES : contrairement aux exemples étiquetés PROUVÉS ou RÉFUSÉS, il n'y a pas de chaîne de réflexion naturelle pour les exemples étiquetés INCONNUS.

Pour les problèmes de chaîne de preuve plus profonds (3+), SI produit des prédictions proches des prédictions de la classe majoritaire sur trois ensembles de données.

On peut constater que dans le cas binaire, il a tendance à surestimer REFUSÉ ; dans le cas de classification ternaire, il a tendance à surestimer INCONNU, ce qui le rend encore plus performant que la classe majoritaire en profondeur-5 de PrOntoQA Bad car il y a plus de balises PROVÉES que REFUSÉES à cette profondeur.

Cependant, les chercheurs ont également été surpris de constater que les performances de CoT sur l'ensemble de données ProofWriterPD étaient encore relativement élevées et que le taux de précision n'a pas diminué.

En résumé, sur ces ensembles de données, LAMBADA a une précision d'inférence plus élevée que d'autres techniques qui trouvent des conclusions correctes avec de fausses traces de preuve, LAMBADA est plus susceptible de produire des chaînes d'inférence valides que les autres techniques de raisonnement modulaire basées sur LM. est plus efficace dans la requête.

Les résultats de cette expérience suggèrent fortement que les futurs travaux sur le raisonnement avec LM devraient inclure un chaînage en arrière ou des stratégies orientées vers un objectif, ont déclaré les chercheurs.

Référence :​

https://arxiv.org/abs/2212.13894

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!