Conception et mise en œuvre d'un système de surveillance des anomalies de bases de données basé sur un algorithme d'IA

Auteur : Cao Zhen Weiyuan

L'équipe R&D de la plateforme de bases de données Meituan est confrontée au besoin de plus en plus urgent de détecter les anomalies des bases de données Afin de découvrir, localiser et arrêter les pertes plus rapidement et intelligemment, nous avons développé un service de détection des anomalies des bases de données basé sur l'IA. algorithmes.

1. Contexte

La base de données est largement utilisée dans les scénarios commerciaux de base de Meituan, avec des exigences de stabilité élevées et une très faible tolérance aux exceptions. Par conséquent, la découverte rapide des anomalies dans les bases de données, leur localisation et leur arrêt des pertes deviennent de plus en plus importants. En réponse au problème de surveillance anormale, la méthode traditionnelle d'alarme à seuil fixe nécessite une expérience experte pour configurer les règles et ne peut pas ajuster le seuil de manière flexible et dynamique en fonction de différents scénarios commerciaux, ce qui peut facilement transformer de petits problèmes en échecs majeurs.

La capacité de découverte des anomalies de la base de données basée sur l'IA peut effectuer des inspections 7 heures sur 24 des indicateurs clés en fonction des performances historiques de la base de données. Elle peut détecter les risques à l'origine des anomalies, les exposer plus tôt et aider le personnel de R&D. . Localisez et arrêtez les pertes avant que les problèmes ne s'aggravent. Sur la base des considérations des facteurs ci-dessus, l'équipe R&D de la plate-forme de base de données Meituan a décidé de développer un système de service de détection d'anomalies de base de données. Ensuite, cet article développera certaines de nos réflexions et pratiques dans plusieurs dimensions telles que l'analyse des fonctionnalités, la sélection d'algorithmes, la formation de modèles et la détection en temps réel.

2. Analyse des fonctionnalités

2.1 Découvrez les modèles changeants des données

Avant d'effectuer un développement et un codage spécifiques, il y a une tâche très importante, qui consiste à découvrir les modèles changeants des données de séries chronologiques à partir de la surveillance historique existante. indicateurs Ainsi, un algorithme approprié peut être sélectionné en fonction des caractéristiques de la distribution des données. Voici quelques graphiques représentatifs de distribution d'indicateurs que nous avons sélectionnés à partir de données historiques :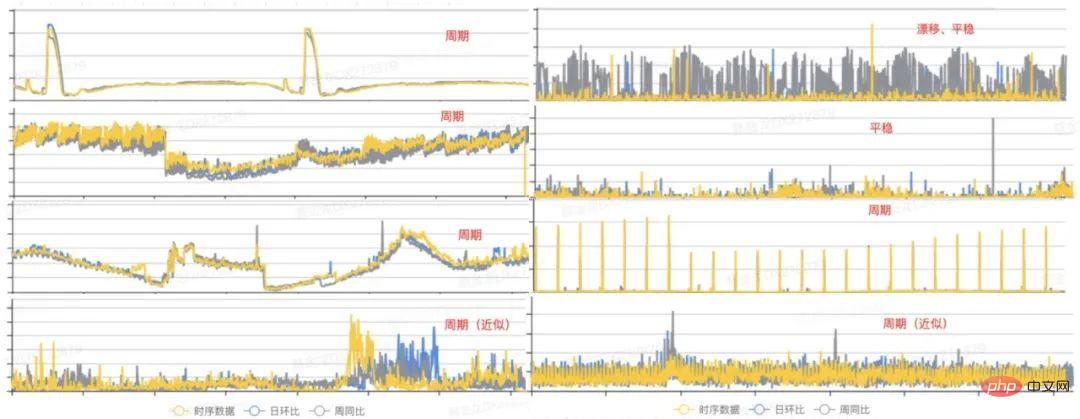

Figure 1 Formulaire d'indicateur de base de données

À partir de la figure ci-dessus, nous pouvons voir que les modèles de données présentent principalement trois états : Période, dérive et plateau ^[1]. Par conséquent, nous pouvons modéliser des échantillons présentant ces caractéristiques communes à un stade précoce, ce qui peut couvrir la plupart des scénarios. Ensuite, nous l’analysons sous trois perspectives : périodicité, dérive et stationnarité, et discutons du processus de conception de l’algorithme.

2.1.1 Changements cycliques

Dans de nombreux scénarios commerciaux, les indicateurs fluctueront régulièrement en raison des pics du matin et du soir ou de certaines tâches planifiées. Nous pensons qu'il s'agit d'une fluctuation régulière inhérente aux données et que le modèle devrait avoir la capacité d'identifier les composantes périodiques et de détecter les anomalies contextuelles. Pour les indicateurs de séries chronologiques qui n'ont pas de composante de tendance à long terme, lorsque l'indicateur a une composante cyclique, 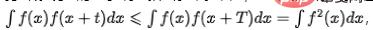, où T représente la période de la série chronologique. Le diagramme d'autocorrélation peut être calculé, c'est-à-dire la valeur de 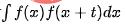lorsque t prend différentes valeurs, puis la périodicité peut être déterminée en analysant les intervalles des pics d'autocorrélation. Le processus principal comprend les étapes suivantes :

1. . Extrayez les composants de tendance pour isoler la séquence résiduelle. Utilisez la méthode de la moyenne mobile pour extraire le terme de tendance à long terme, et faites la différence avec la séquence d'origine pour obtenir la séquence résiduelle (Ici, l'analyse périodique n'a rien à voir avec la tendance. Si la composante de tendance n'est pas séparée , l'autocorrélation sera considérablement affectée, ce qui rendra difficile l'identification de la période ).
2. Calculez la séquence d'autocorrélation roulante (Rolling Correlation) des résidus. La séquence d'autocorrélation est calculée en effectuant une opération de multiplication de points vectoriels avec la séquence résiduelle après avoir décalé cycliquement la séquence résiduelle (l'autocorrélation cyclique peut éviter une décroissance retardée).
3. La période T est déterminée en fonction de la coordonnée maximale de la séquence d'autocorrélation. Extraire une série de pics locaux les plus élevés de la séquence d'autocorrélation, et prendre l'intervalle de l'abscisse comme période (Si la valeur d'autocorrélation correspondant au point périodique est inférieure au seuil donné, elle est considérée comme n'ayant pas de périodicité significative) .

Le processus spécifique est le suivant :

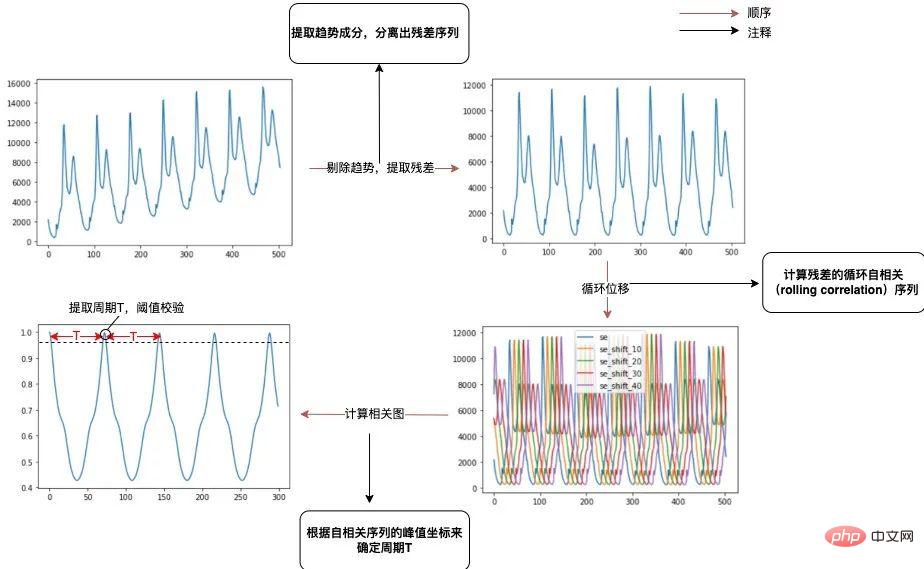
Figure 2 Schéma du processus d'extraction du cycle

2.1.2 Changements de dérive

Pour que la séquence à modéliser, il est généralement requis qu'elle ne présente pas de tendance évidente à long terme ou de dérive globale phénomène, sinon les modèles générés ne s'adaptent souvent pas bien aux tendances récentes des indicateurs ^[2]. Nous faisons référence à des situations dans lesquelles la valeur moyenne d'une série chronologique change de manière significative au fil du temps ou où il existe un point de mutation global, collectivement appelés scénario de dérive. Afin de capturer avec précision la dernière tendance de la série chronologique, nous devons déterminer s'il y a une dérive dans les données historiques au début de la modélisation. La dérive globale et les séries périodiques signifient la dérive, comme le montre l'exemple suivant :

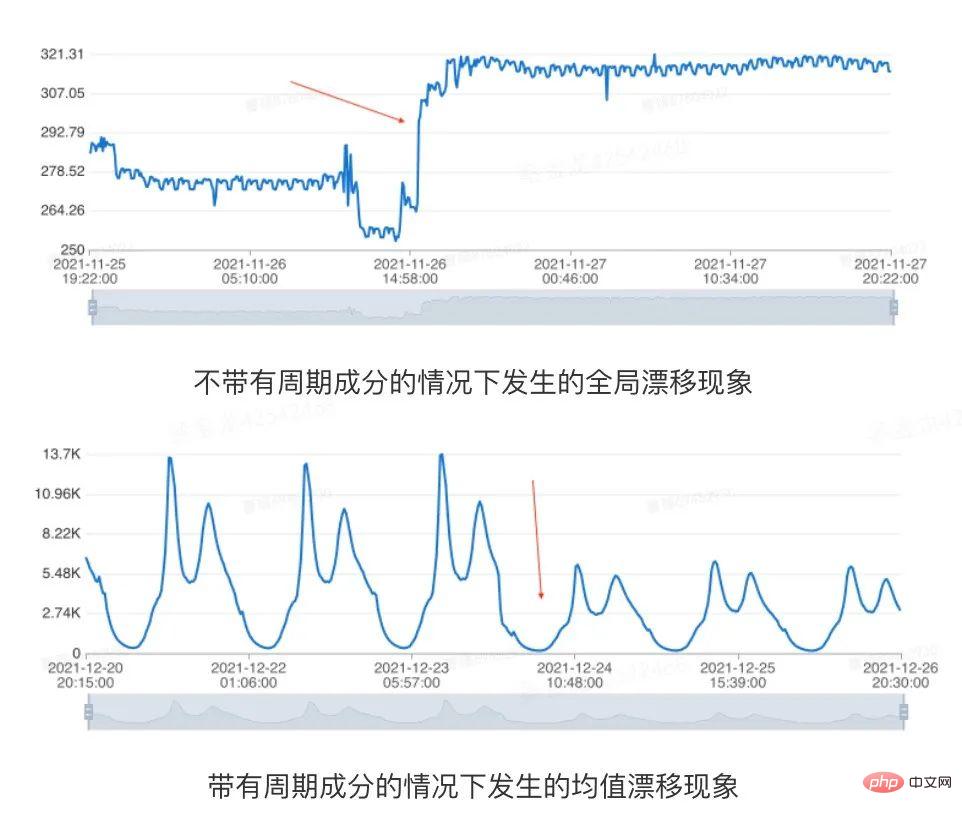
Figure 3 Dérive des données

Les indicateurs de base de données sont affectés par des facteurs complexes tels que les activités commerciales, et de nombreuses données auront une forme non périodique. changements. Et la modélisation doit tolérer ces changements. Par conséquent, contrairement au problème classique de détection de points de changement, dans le scénario de détection d’anomalies, il suffit de détecter la situation dans laquelle les données sont stables dans l’historique puis dérivent. Sur la base des performances de l'algorithme et des performances réelles, nous avons utilisé la méthode de détection de dérive basée sur le filtrage médian. Le processus principal comprend les liens suivants :

1. Lissage médian

a. de la fenêtre, et la médiane à l'intérieur de la fenêtre est extraite pour obtenir la composante de tendance de la série chronologique.

b. La fenêtre doit être suffisamment grande pour éviter l'influence de facteurs périodiques et effectuer une correction du retard du filtre.

c. La raison d'utiliser le lissage médian plutôt que moyen est d'éviter l'influence d'échantillons anormaux.

2. Déterminez si la séquence lissée est croissante ou décroissante

a Pour les données de séquence après lissage médian, si chaque point est supérieur (inférieur à) le point précédent, la séquence est. séquence croissante (Diminution).

b. Si la séquence est strictement croissante ou strictement décroissante, alors l'indicateur a évidemment une tendance à long terme, et il peut être terminé plus tôt.

3. Parcourez la séquence fluide et utilisez les deux règles suivantes pour déterminer s'il y a une dérive

a Si la valeur maximale de la séquence à gauche du point d'échantillonnage actuel est inférieure à la valeur maximale de la séquence à gauche du point d'échantillonnage actuel. valeur minimale de la séquence à droite du point d'échantillonnage actuel, alors il y a Sudden Drift (Uptrend).

b. Si la valeur minimale de la séquence à gauche du point d'échantillonnage actuel est supérieure à la valeur maximale de la séquence à droite du point d'échantillonnage actuel, il y a une dérive de chute soudaine (tendance baissière) .

2.1.3 Changements stationnaires

Pour un indicateur de série chronologique, si ses propriétés ne changent pas avec le changement de temps d'observation à tout moment, nous pensons que cette série chronologique est stationnaire. Par conséquent, pour les séries chronologiques comportant des composantes de tendance à long terme ou des composantes cycliques, elles sont toutes non stationnaires. L'exemple spécifique est présenté dans la figure ci-dessous :

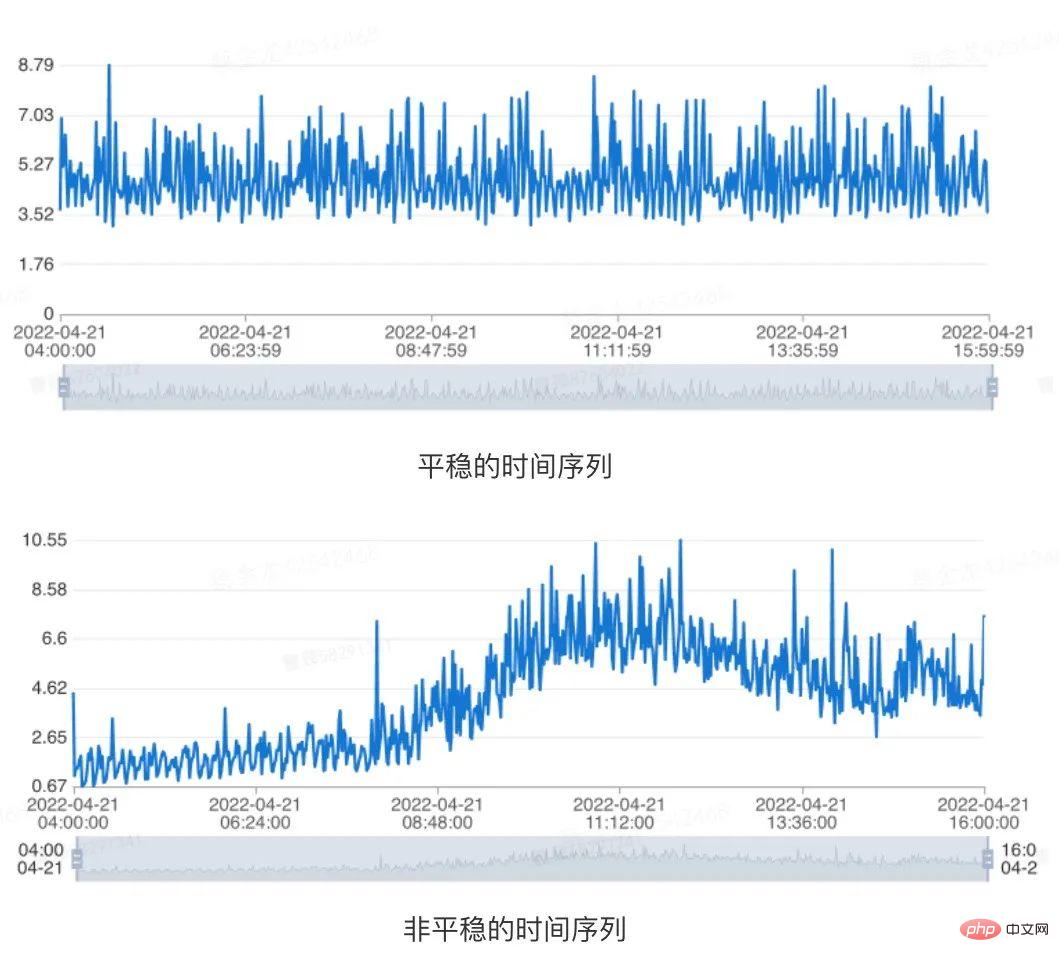
Figure 4 Indication de stationnarité des données

Dans ce cas, nous pouvons juger par test de racine unitaire (Test Dickey-Fuller augmenté)^[3] Si une série chronologique donnée est stationnaire. Plus précisément, pour une donnée historique d'un indicateur de plage temporelle donnée, nous pensons que la série chronologique est stable lorsque les conditions suivantes sont remplies en même temps :

1. La valeur p obtenue par le test Adfuller pour les données de séries chronologiques du dernier jour est inférieure à 0,05.
2. La valeur p obtenue par le test Adfuller pour les données de séries chronologiques des 7 derniers jours est inférieure à 0,05.

3. Sélection d'algorithmes

3.1 Loi de distribution et sélection d'algorithmes

En comprenant les introductions de produits publiées par certaines sociétés bien connues du secteur sur la détection d'anomalies de données de séries chronologiques, associées à notre expérience historique accumulée et partielle analyse de ligne Sur la base de l'analyse d'échantillonnage des indicateurs réels, leurs fonctions de densité de probabilité sont conformes à la distribution suivante :

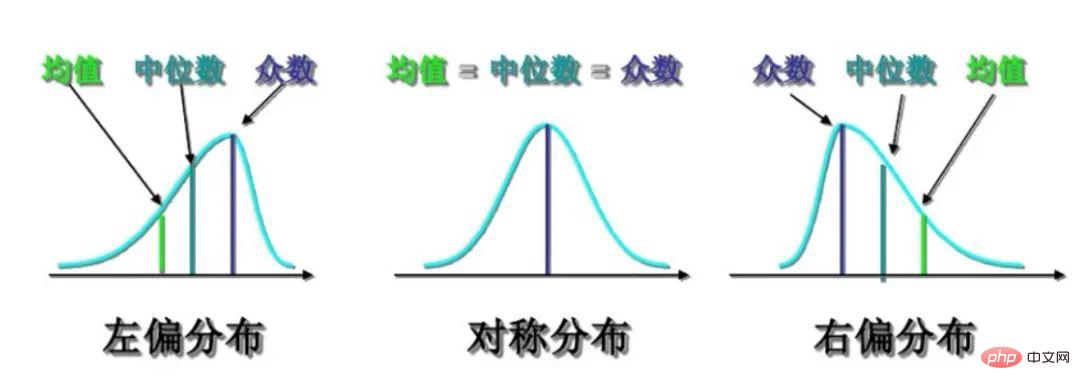
Figure 5 Asymétrie de la distribution

En visant la distribution ci-dessus, nous avons étudié certains algorithmes courants et déterminé la boîte le tracé, la différence médiane absolue et la théorie des valeurs extrêmes sont utilisés comme algorithme final de détection des anomalies. Ce qui suit est un tableau comparatif des algorithmes pour la détection de données de séries chronologiques courantes :

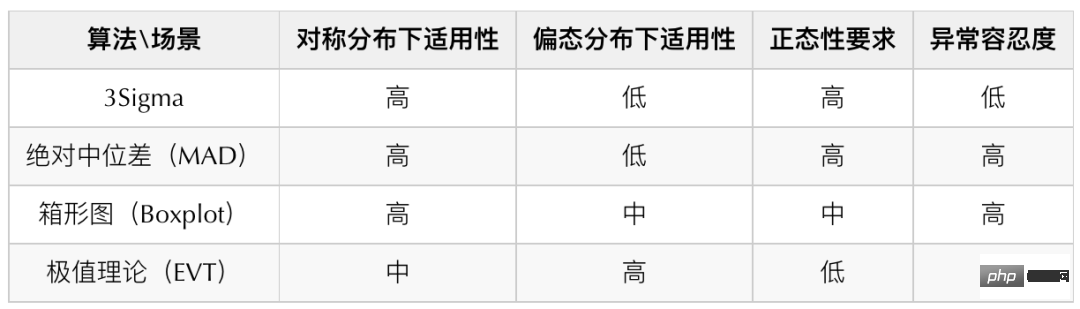
La principale raison pour laquelle nous n'avons pas choisi 3Sigma est qu'il a une tolérance plus faible pour les anomalies, alors que la différence médiane absolue présente théoriquement de meilleures anomalies. Tolérance, ainsi lorsque les données présentent une distribution hautement symétrique, la différence médiane absolue (MAD) est utilisée à la place de 3Sigma pour la détection. Nous utilisons différents algorithmes de détection pour la distribution des différentes données (Pour les principes des différents algorithmes, veuillez vous référer à l'annexe en fin d'article, je ne m'étendrai pas trop ici) :

1. Faible asymétrie et distribution à symétrie élevée : Différence médiane absolue (MAD)
2. Distribution modérément asymétrique : Boxplot (Boxplot)
3. Distribution fortement asymétrique : Théorie des valeurs extrêmes (EVT )

Avec l'analyse ci-dessus, nous pouvons obtenir le processus spécifique de sortie du modèle basé sur l'échantillon :

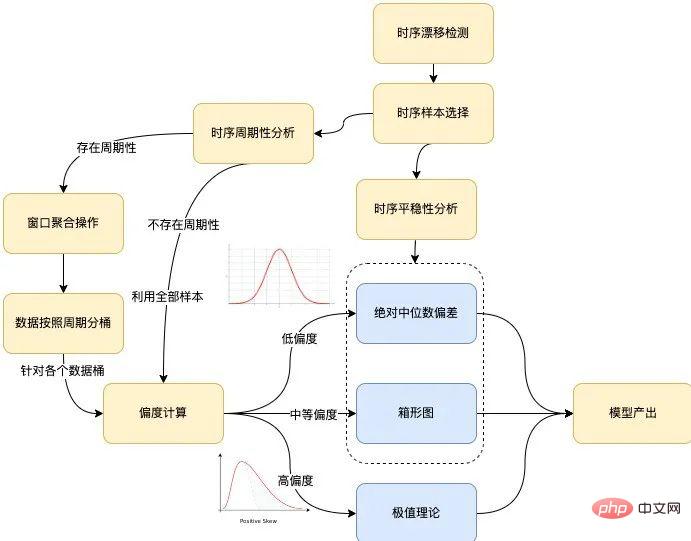
Figure 6 Processus de modélisation de l'algorithme

Le processus de modélisation global de l'algorithme est illustré dans le figure ci-dessus, il couvre principalement les branches suivantes : détection de dérive temporelle, analyse de stabilité temporelle, analyse de périodicité temporelle et calcul d'asymétrie. Les éléments suivants sont présentés séparément :

1. Détection de dérive temporelle. Si la scène où une dérive existe est détectée, la série temporelle d'entrée doit être découpée en fonction du point de dérive t obtenu par la détection, et les échantillons de séries temporelles après le point de dérive sont utilisés comme entrée du processus de modélisation ultérieur, enregistrés comme S={Si}, où i>t.
2. Analyse de stationnarité des séries chronologiques. Si la série temporelle d'entrée S satisfait au test de stationnarité, elle sera modélisée directement via le box plot (par défaut) ou la différence médiane absolue.
3. Analyse périodique des séries chronologiques. Dans le cas de la périodicité, la période est enregistrée comme T, la série temporelle d'entrée S est découpée en fonction de la période T et le processus de modélisation est effectué pour le compartiment de données composé de chaque indice temporel j∈{0,1, ⋯,T−1} . En l'absence de périodicité, le processus de modélisation est effectué pour toutes les séries temporelles d'entrée S sous forme de compartiments de données.

Cas  : Étant donné une série temporelle ts={t₀,t₁,⋯,t_n}, en supposant qu'elle a une périodicité et que la période est T, pour l'indice temporel j En termes de , où j∈{0,1,⋯,T−1}, les points d'échantillonnage requis pour le modéliser sont constitués de l'intervalle [t_j−kT−m, t_j−kT+m] , Où m est un paramètre représentant la taille de la fenêtre, k est un entier satisfaisant j−kT−m≥0, j−kT+m≤n. Par exemple, en supposant que la série chronologique donnée commence du 01/03/2022 00:00:00 au 08/03/2022 00:00:00, la taille de la fenêtre donnée est de 5 et la période est d'un jour, alors pour l'indice temporel 30 Autrement dit, les points d'échantillonnage nécessaires à sa modélisation proviendront de la période temporelle suivante : [03/01 00:25:00, 03/01 00:35:00]
[03/02 00:25 :00, 03/02 00:35:00]
...
[03/07 00:25:00, 03/07 00:35:00]

4. calcul d'asymétrie. Les indicateurs de séries chronologiques sont convertis en diagrammes de distribution de probabilité et l'asymétrie de la distribution est calculée si la valeur absolue de l'asymétrie dépasse le seuil, la théorie des valeurs extrêmes est utilisée pour modéliser le seuil de sortie. Si la valeur absolue de l'asymétrie est inférieure au seuil, le seuil est modélisé et généré par une boîte à moustaches ou une différence médiane absolue.

3.2 Modélisation d'échantillons de cas

Un cas est sélectionné ici pour montrer le processus d'analyse et de modélisation des données afin de faciliter une compréhension plus claire du processus ci-dessus. La figure (a) est la séquence originale, la figure (b) est la séquence repliée en fonction de l'intervalle de jours, la figure (c) est la performance de tendance amplifiée des échantillons dans un certain intervalle d'indice de temps dans la figure (b), la figure ( d) ) est le seuil inférieur correspondant à l'indice de temps de la figure (c). Ce qui suit est un cas de modélisation d'échantillons historiques d'une certaine série chronologique :

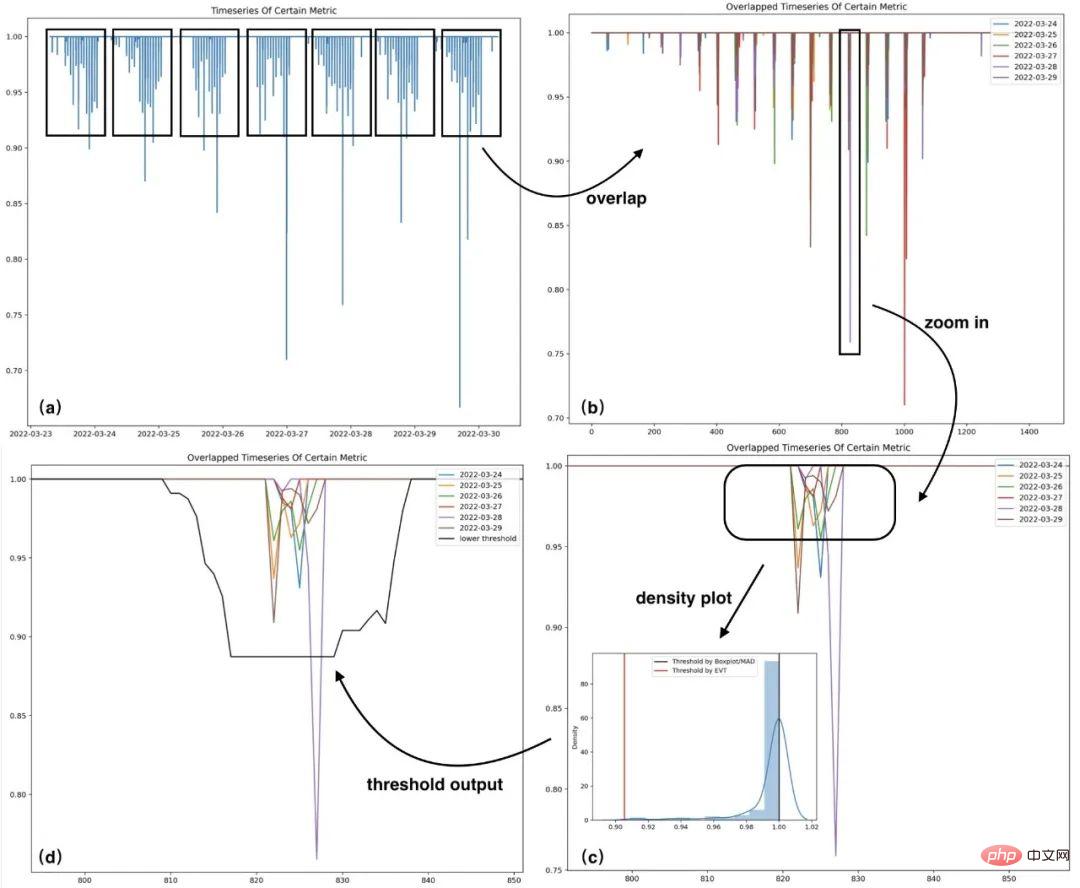
Figure 7 Cas de modélisation

L'histogramme de distribution d'échantillon et le seuil dans la zone (c) de la figure ci-dessus (Certains des ils ont été supprimés Échantillon anormal ), on constate que dans ce scénario de distribution très asymétrique, le seuil calculé par l'algorithme EVT est plus raisonnable.

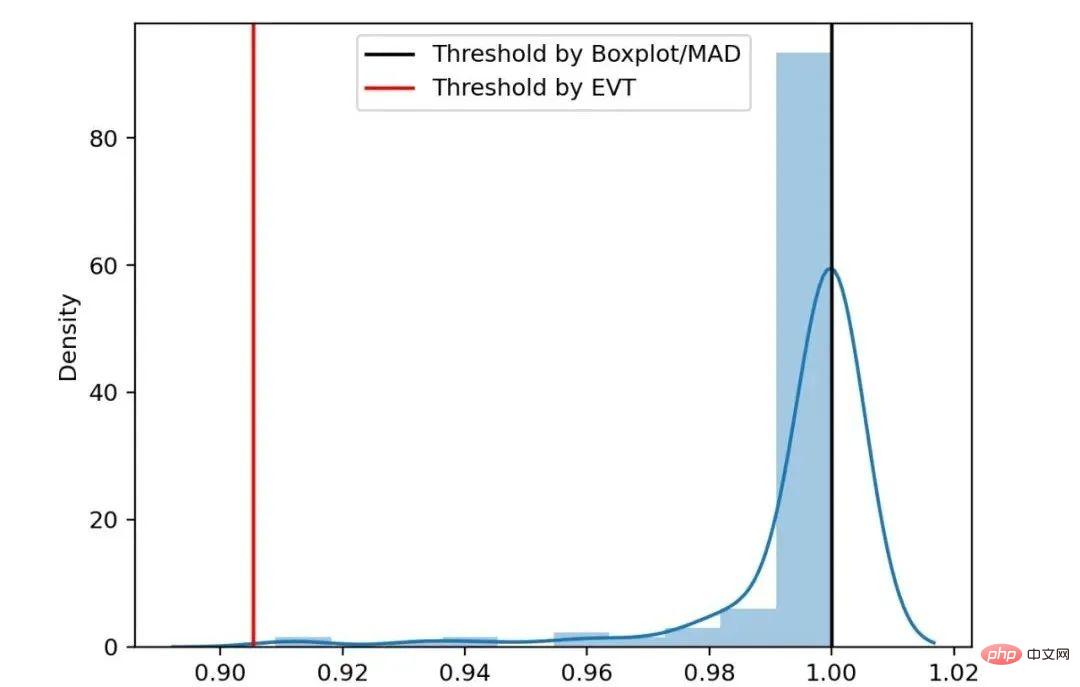
Figure 8 Comparaison des seuils de distribution asymétrique

4. Formation du modèle et détection en temps réel

4.1 Processus de flux de données

Afin de détecter des données de deuxième niveau à grande échelle en temps réel, nous utilisons Flink pour le streaming en temps réel En prenant le traitement comme point de départ, nous avons conçu les solutions techniques suivantes :

1. Partie de détection en temps réel : Basé sur le traitement du flux en temps réel Flink, il consomme les messages Mafka (composant de file d'attente de messages interne de Meituan) pour la détection en ligne, et les résultats sont stockés dans Elasticsearch (ci-après dénommé ES) ) et générer un enregistrement d'exception.
2. Partie formation hors ligne : utilisez Squirrel (base de données KV interne de Meituan) comme file d'attente des tâches, lisez les données de formation à partir du MOD (entrepôt de données d'exploitation et de maintenance interne de Meituan) et lisez les paramètres de la table de configuration, le modèle de formation est enregistré dans ES, prend en charge le déclenchement automatique et manuel de la formation, et charge et met à jour le modèle en lisant régulièrement la bibliothèque de modèles.

Ce qui suit est la conception spécifique de la formation hors ligne et de la technologie de détection en ligne :

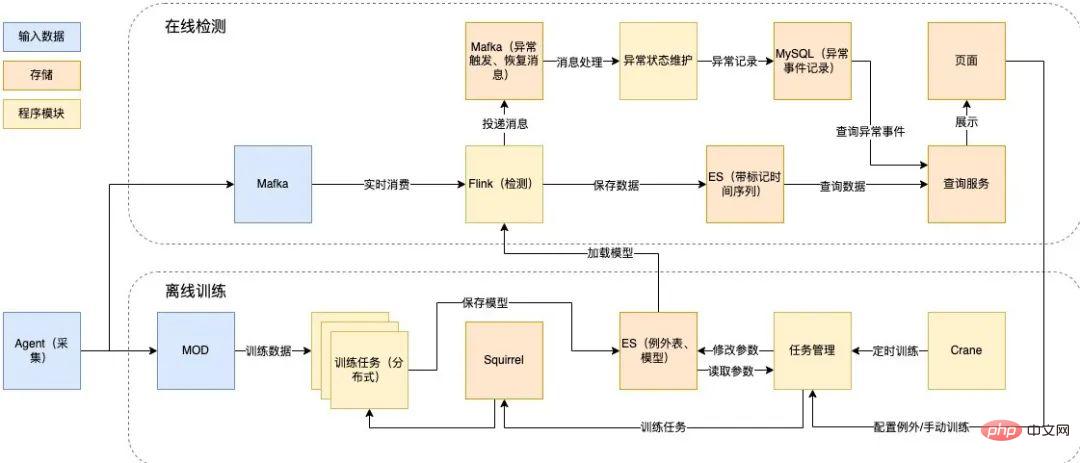
Figure 9 Formation hors ligne et conception de la technologie de détection en ligne

4.2 Processus de détection des anomalies

L'algorithme global de détection des anomalies adopte diviser pour mieux régner L'idée est qu'au cours de la phase de formation du modèle, les caractéristiques sont extraites sur la base de l'identification des données historiques et un algorithme de détection approprié est sélectionné. Ceci est divisé en deux parties : la formation hors ligne et la détection en ligne effectuent principalement le prétraitement des données, la classification des séries chronologiques et la modélisation des séries chronologiques en fonction des conditions historiques. Online charge et utilise principalement des modèles formés hors ligne pour la détection d'anomalies en ligne et en temps réel. La conception spécifique est présentée dans la figure ci-dessous :

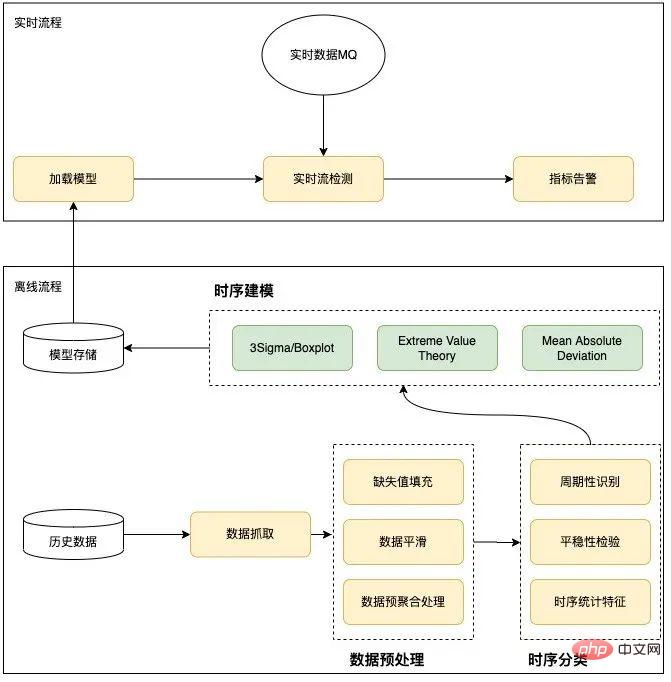
Figure 10 Processus de détection d'anomalies

5. Fonctionnement du produit

Afin d'améliorer l'efficacité de l'algorithme itératif d'optimisation et de poursuivre les opérations pour améliorer précision et rappel, nous Avec l'aide des capacités d'examen des cas Horae (le système interne évolutif de détection des anomalies de données de séries chronologiques de Meituan), une boucle fermée de détection en ligne, de sauvegarde des cas, d'optimisation de l'analyse, d'évaluation des résultats et de publication est réalisée.

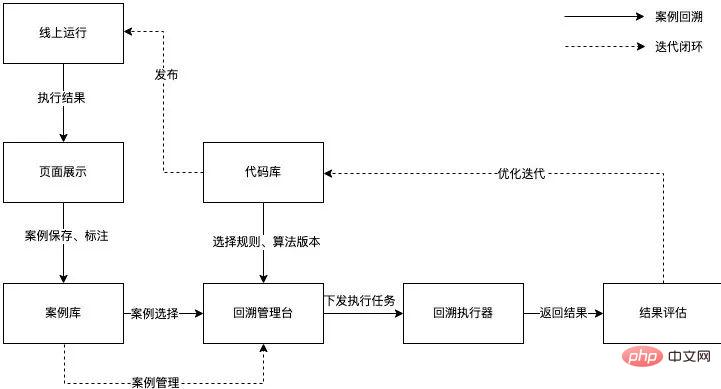
Figure 11 Processus de fonctionnement

Actuellement, les indicateurs de l'algorithme de détection d'anomalies sont les suivants :

• Taux de précision  : sélectionner au hasard un une partie des cas où des anomalies sont détectés, et les vérifier manuellement. Il s'agit bien d'une proportion anormale, 81 %.
• Taux de rappel : en fonction des défauts, des alarmes et d'autres sources, examinez les conditions anormales de chaque indicateur de l'instance correspondante et calculez le taux de rappel en fonction des résultats de surveillance, qui est de 82 %.
• F1-score : La moyenne harmonique de précision et de rappel, qui est de 81 %.

6. Perspectives d'avenir

À l'heure actuelle, la capacité de surveillance des anomalies de la base de données de Meituan est pratiquement terminée. Nous continuerons à optimiser et à développer le produit à l'avenir.

1. Possède une capacité de reconnaissance de type d'exception. Il peut détecter des types anormaux, tels que des changements moyens, des changements de fluctuation, des pics, etc., prend en charge l'abonnement aux alarmes en fonction des types anormaux et les saisit en tant que fonctionnalités dans le système de diagnostic ultérieur, améliorant l'écosystème d'autonomie de la base de données^[4] .
2. Créer un environnement Human-in-Loop. Prend en charge l'apprentissage automatique basé sur l'annotation des commentaires, garantissant une optimisation continue du modèle^[5].
3. Prise en charge de plusieurs scénarios de bases de données. La capacité de détection des anomalies est basée sur une plate-forme pour prendre en charge davantage de scénarios de bases de données, tels que le rapport d'erreurs de bout en bout de base de données, la surveillance du réseau de nœuds, etc.

7. Annexe

7.1 Déviation médiane absolue

L'écart médian absolu, c'est-à-dire l'écart médian absolu (MAD), est une mesure robuste de l'écart d'échantillon de données numériques univariées ^[6], généralement calculé par la formule suivante :

où, lorsque l'a priori est une distribution normale, généralement C choisit 1,4826 et k choisit 3. MAD suppose que les 50 % du milieu des échantillons sont des échantillons normaux, tandis que les échantillons anormaux se situent dans les zones de 50 % des deux côtés. Lorsque l'échantillon obéit à la distribution normale, l'indicateur MAD est mieux à même de s'adapter aux valeurs aberrantes de l'ensemble de données que l'écart type. Pour l'écart type, le carré de la distance entre les données et la moyenne est utilisé. Des écarts plus importants ont un poids plus important. Pour MAD, un petit nombre de valeurs aberrantes n'affectera pas les résultats. de l'expérience. L'algorithme MAD a un plus grand impact sur les données. Les exigences de normalité sont plus élevées.

7.2 Box plot

Le box plot décrit principalement le caractère discret et la symétrie de la distribution de l'échantillon à travers plusieurs statistiques, notamment :

• Q0 : Valeur minimale (Minimum)
• Q1 : Quartile inférieur Maximum (Maximum)
• Figure 12 Boxplot
• La distance entre Q1 et Q

3

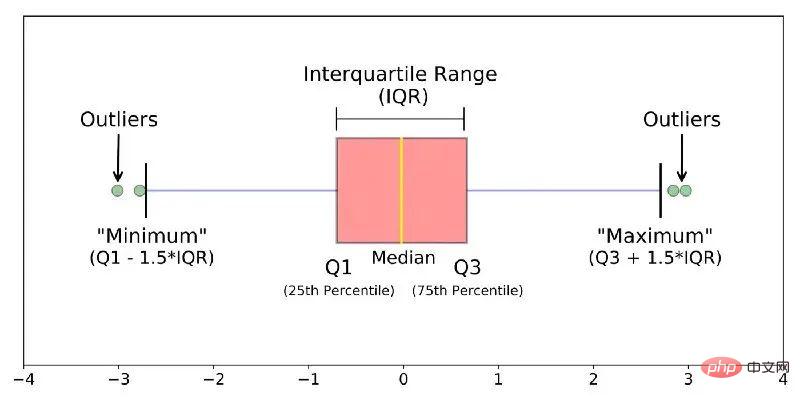est appelé IQR, lorsque l'échantillon Lorsque l'IQR s'écarte du quartile supérieur de 1,5 fois (

ou s'écarte de l'IQR de 1,5 fois par rapport au quartile inférieur), l'échantillon est considéré comme une valeur aberrante. Contrairement aux trois écarts types basés sur l'hypothèse de normalité, les boîtes à moustaches ne font généralement aucune hypothèse sur la distribution sous-jacente des données de l'échantillon, peuvent décrire la situation discrète de l'échantillon et ont une plus grande confiance dans les échantillons anormaux potentiels contenus dans l'échantillon. . Tolérance. Pour les données biaisées, la modélisation calibrée de Boxplot est plus cohérente avec la distribution des données

[7].

7.3 Théorie des valeurs extrêmes_{Les données du monde réel sont difficiles à résumer avec une distribution connue. Par exemple, pour certains événements extrêmes (}anormaux), les modèles de probabilité (tels que la distribution gaussienne_{) donnent souvent la probabilité. est 0. La théorie des valeurs extrêmes}[8] consiste à déduire la distribution des événements extrêmes que nous pouvons observer sans aucune hypothèse de distribution basée sur les données originales. Il s'agit de la distribution des valeurs extrêmes (EVD). Son expression mathématique est la suivante (Formule de fonction de distribution cumulée complémentaire^{) :}

où t représente le seuil empirique de l'échantillon. Différentes valeurs peuvent être définies pour différents scénarios, qui sont les paramètres de forme et les paramètres d'échelle dans la distribution de Pareto généralisée. Lorsqu'un échantillon donné dépasse le seuil empirique t artificiellement défini, le la variable aléatoire X-t obéit à la distribution de Pareto généralisée. Grâce à la méthode d'estimation du maximum de vraisemblance, nous pouvons calculer les estimations des paramètres et et obtenir le seuil du modèle grâce à la formule suivante :

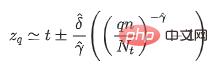
Dans la formule ci-dessus, q représente le paramètre de risque, n est le nombre de tous les échantillons , et Nt est le nombre d'échantillons pour x-t>0. Puisqu'il n'existe généralement aucune information a priori pour estimer le seuil empirique t, le quantile empirique de l'échantillon peut être utilisé pour remplacer la valeur numérique t. La valeur du quantile empirique peut ici être sélectionnée en fonction de la situation réelle.

8. Références

[1] Ren, H., Xu, B., Wang, Y., Yi, C., Huang, C., Kou, X., ... et Zhang, Q . (juillet 2019). Service de détection d'anomalies de séries chronologiques chez Microsoft. Dans Actes de la 25e conférence internationale ACM SIGKDD sur la découverte de connaissances et l'exploration de données (pp. 3009-3017).

[2] Lu, J., Liu. , A., Dong, F., Gu, F., Gama, J. et Zhang, G. (2018). Apprentissage sous la dérive des concepts : une revue des transactions IEEE sur l'ingénierie des connaissances et des données, 31(12), 2346. -2363.

[3] Mushtaq, R. (2011). Test de Dickey Fuller augmenté.

[4] Ma, M., Yin, Z., Zhang, S., Wang, S., Zheng, C., Jiang, X., ... & Pei, D. (2020). Diagnostic des causes profondes des requêtes lentes intermittentes dans les bases de données cloud Proceedings of the VLDB Endowment, 13(8), 1176-1189.

[. 5] Holzinger, A. (2016). Apprentissage automatique interactif pour l'informatique de la santé : quand avons-nous besoin de l'humain dans la boucle ?. Brain Informatics, 3(2), 119-131.

[6] Leys. , C., Ley, C., Klein, O., Bernard, P. et Licata, L. (2013). Détection des valeurs aberrantes : n'utilisez pas l'écart type autour de la moyenne, utilisez l'écart absolu autour de la médiane. psychologie sociale, 49(4), 764-766.

[7] Hubert, M. et Vandervieren, E. (2008). Une boîte à moustaches ajustée pour les distributions asymétriques et l'analyse des données, 52(12), . 5186-5201.

[8] Siffer, A., Fouque, P. A., Termier, A. et Largouet, C. (2017, août). Détection d'anomalies dans les cours d'eau avec théorie des valeurs extrêmes. Conférence internationale SIGKDD sur la découverte des connaissances et l'exploration de données (pp. 1067-1075).

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!