Boaz Barak, informaticien théorique : l’apprentissage profond n’est pas de « simples statistiques » et les deux s’éloignent de plus en plus

Dans les années 1990, Rob Tibshirani, professeur bien connu de bioinformatique à l'université de Stanford, a élaboré un vocabulaire pour établir une correspondance simple et grossière entre différents concepts d'apprentissage automatique et de statistiques :

Sur l'un D'une part, ce tableau fournit une compréhension de base de l'apprentissage automatique, mais en même temps, il résume simplement les concepts d'apprentissage profond ou d'apprentissage automatique en significations de mots dans les statistiques, ce qui suscite également les doutes de la plupart des gens sur la nature du biais cognitif. : Le deep learning est une « simple statistique ».

Cependant, lors de discussions approfondies, une telle perception a empêché dans une certaine mesure les chercheurs de comprendre les raisons essentielles du succès de l'apprentissage profond. Dans un article intitulé « La relation difficile entre l'apprentissage profond et les statistiques (classiques) » paru en juin de cette année, Boaz Barak, professeur bien connu à Harvard et informaticien théoricien, a comparé et distingué l'apprentissage profond et les statistiques, soulignant les principes fondamentaux de l'apprentissage profond. Les facteurs constitutifs sont très différents des statistiques.

Boaz Barak a fait une observation importante : du point de vue de l'objectif du modèle, s'il se concentre sur la prédiction et l'observation, alors un modèle d'apprentissage profond avec les caractéristiques d'une boîte noire peut être le meilleur choix ; la cause et l'effet des choses Compréhension des relations et interprétabilité améliorée, les modèles « simples » peuvent alors mieux fonctionner. Cela coïncide avec l'idée de « simplicité » qui constitue l'un des deux principes de l'intelligence proposés le mois dernier par trois scientifiques : Ma Yi, Cao Ying et Shen Xiangyang.

Dans le même temps, Boaz Barak a discuté de sa compatibilité avec l'apprentissage profond en montrant deux cas de scénario différents d'ajustement de modèles statistiques et d'apprentissage des mathématiques ; Le modèle est presque le même, mais à un niveau plus profond, une grande partie de l'apprentissage profond peut être capturée dans le scénario « enseigner des compétences aux étudiants ».

L'apprentissage statistique joue un rôle important dans le deep learning, cela ne fait aucun doute. Mais ce qui est certain, c’est que la perspective statistique ne peut pas fournir une image complète de la compréhension du deep learning. Pour comprendre les différents aspects du deep learning, il faut encore l’aborder sous différents angles.

Voici la discussion de Boaz Barak :

1 Prédiction et explication dans l'ajustement de modèles

Depuis des milliers d'années, les scientifiques ajustent des modèles aux observations. Par exemple, comme mentionné dans la couverture du livre Philosophy of Science, l’astronome égyptien Ptolémée a proposé un ingénieux modèle du mouvement planétaire. Le modèle de Ptolémée était géocentrique (c'est-à-dire que les planètes tournaient autour de la Terre), mais comportait une série de « boutons » (en particulier des épicycles) qui lui conféraient une excellente précision prédictive. En revanche, le modèle héliocentrique original de Copernic supposait des orbites circulaires des planètes autour du soleil. Il est plus simple que le modèle de Ptolémée (moins de « boutons réglables ») et globalement plus correct, mais moins précis dans la prédiction des observations . (Copernic a également ajouté plus tard ses propres épicycles, les rendant comparables aux performances de Ptolémée.)

Les modèles ptolémaïques et coperniciens sont sans précédent. Lorsque vous avez besoin d’une « boîte noire » pour faire des prédictions, le modèle géocentrique ptolémaïque est supérieur. Et si vous voulez un modèle simple qui puisse « jeter un œil à l’intérieur » et servir de point de départ théorique pour expliquer les mouvements des étoiles, alors le modèle de Copernic est meilleur.

En fait, Kepler a finalement affiné le modèle de Copernic en orbites elliptiques et a proposé ses trois lois du mouvement planétaire, ce qui a permis à Newton de les expliquer en utilisant les mêmes lois de la gravité qui s'appliquent sur Terre. À cette fin, il est crucial que le modèle héliocentrique ne soit pas simplement une « boîte noire » fournissant des prédictions, mais qu’il soit plutôt donné par de simples équations mathématiques comportant peu de « pièces mobiles ». L’astronomie est depuis de nombreuses années une source d’inspiration pour le développement de techniques statistiques. Gauss et Legendre (indépendamment) ont inventé la régression des moindres carrés vers 1800 pour prédire les orbites des astéroïdes et d'autres corps célestes ; l'invention de la descente de gradient par Cauchy en 1847 était également motivée par des prédictions astronomiques.

En physique, (au moins parfois) vous pouvez "tout avoir" - trouver la "bonne" théorie qui permet d'obtenir la meilleure précision de prédiction et la meilleure explication des données, soutenue par des idées telles que le rasoir d'Occam Capturé, la simplicité de l'hypothèse , le pouvoir prédictif et la perspicacité explicative sont tous cohérents les uns avec les autres. Dans de nombreux autres domaines, cependant, il existe une tension entre le double objectif d’explication (ou, plus généralement, de compréhension) et de prédiction. Si vous souhaitez simplement prédire les observations, une « boîte noire » peut être le meilleur choix. Mais si vous extrayez des modèles causals, des principes généraux ou des caractéristiques importantes, un modèle simple, facile à comprendre et à expliquer, pourrait être préférable.

Le bon choix de modèle dépend de sa destination. Par exemple, considérons un ensemble de données contenant l'expression génétique et les phénotypes de nombreux individus (par exemple, pour une certaine maladie). Si l'objectif est de prédire le risque qu'un individu tombe malade, il sera souvent nécessaire d'utiliser le meilleur modèle pour cette tâche. , peu importe la complexité ou le nombre de gènes dont cela dépend. En revanche, si votre objectif est d’identifier quelques gènes en vue d’une étude plus approfondie dans un laboratoire humide, une boîte noire sophistiquée sera d’une utilité limitée, même si elle est très précise.

En 2001, Leo Breiman expliquait effectivement ce point dans son célèbre article « Modélisation statistique : les deux cultures » sur la modélisation statistique. La « culture de modélisation des données » se concentre sur des modèles génératifs simples qui expliquent les données, tandis que la « culture de la modélisation algorithmique » ne comprend pas comment les données sont générées, mais se concentre sur la recherche de modèles capables de prédire les données. Breiman estime que les statistiques sont trop dominées par la culture première et que cette focalisation « conduit à des théories non pertinentes et à des conclusions scientifiques douteuses » et « empêche les statisticiens d'étudier de nouvelles questions passionnantes ».

Cependant, l'article de Breiman est controversé. Bien que Brad Efron soit d'accord avec certains sentiments, « à première vue, l'article passionnant de Leo Breiman semble rejeter la simplicité et la perspicacité scientifique en faveur d'une boîte noire avec de nombreux boutons à manipuler. même." Mais dans un article récent (« Prédiction, Estimation et Attribution »), Efron a généreusement admis qu'« il s'avère que Breiman était plus prémonitoire que moi : Les algorithmes de prédiction pure ont occupé le devant de la scène des statistiques au 21e siècle, et leur développement La direction est similaire à ce que Leo a mentionné précédemment ”

2 Modèles de prédiction classiques et modernes

Que l’apprentissage automatique soit « profond » ou non, il appartient à ce que Breiman appelle la deuxième culture, qui est axée sur la prédiction Cette culture existe depuis longtemps. Par exemple, le manuel de Duda et Hart de 1973 « Deconstructing Distributions: A Pointwise Framework of Learning » et l'article de Highleyman de 1962 « The Design and Analysis of Pattern Recognition Experiments » sont très reconnaissables pour les praticiens de l'apprentissage profond d'aujourd'hui :

. De même, l'ensemble de données de caractères manuscrits de Highleyman et Chow, l'architecture utilisée pour l'adapter (précision d'environ 58 %), trouvent également un écho auprès des lecteurs modernes.

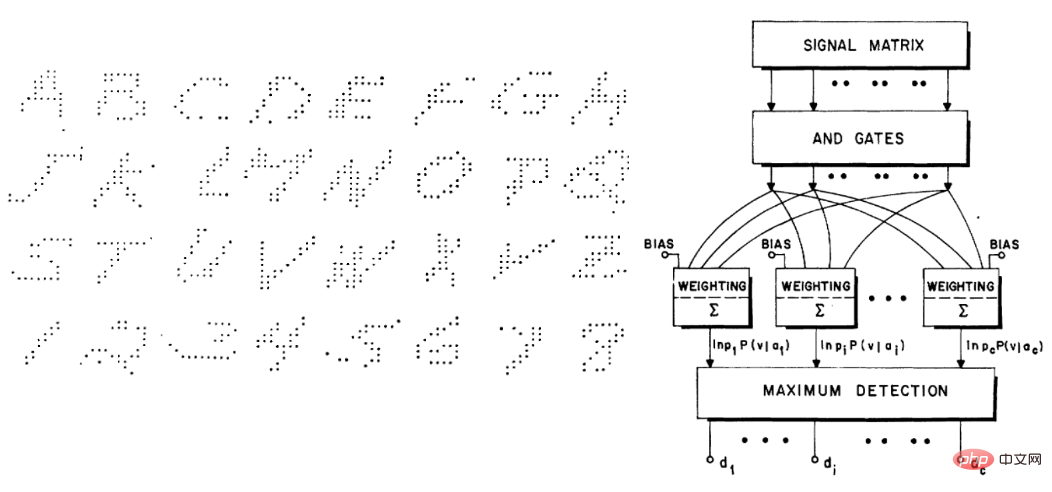
3 Pourquoi l'apprentissage profond est-il différent ?

En 1992, Stuart Geman, Elie Bienenstock et René Doursat ont co-écrit un article intitulé "Neural Networks and the Bias/Varian Dilemma", qui parlait de certains points de vue pessimistes, par exemple, "Current Feedforward Neural Networks" "Networks, sont largement insuffisants pour résoudre des problèmes difficiles de perception et d'apprentissage automatique" ; en particulier, ils soutiennent que les réseaux neuronaux à usage général ne peuvent pas résoudre avec succès des tâches difficiles, et que la seule façon pour les réseaux neuronaux de réussir est de concevoir des fonctionnalités manuellement. Selon leurs mots : "Les fonctionnalités importantes doivent être intégrées ou 'câblées'... plutôt que apprises par des méthodes statistiques.

" Avec le recul, ils ont complètement tort. De plus, les architectures de réseaux neuronaux modernes telles que Transformer sont encore plus polyvalentes que les réseaux convolutifs de l’époque. Mais il est intéressant de comprendre les raisons de leurs erreurs.

Je pense que la raison pour laquelle ils ont commis cette erreur est que le deep learning est en effet différent des autres méthodes d'apprentissage. Un phénomène a priori est le suivant : l'apprentissage profond semble n'avoir qu'un seul modèle de prédiction supplémentaire, comme le voisin le plus proche ou la forêt aléatoire. Il y a peut-être plus de « boutons », mais cela semble être une différence quantitative plutôt que qualitative. Selon les mots de PW Andreson, « plus c'est différent ».

En physique, une fois que l'échelle change de plusieurs ordres de grandeur, nous avons souvent juste besoin d'une théorie complètement différente pour l'expliquer, et il en va de même pour l'apprentissage profond. En fait, le deep learning fonctionne complètement différemment des modèles classiques (paramétriques ou non paramétriques), même si d'un niveau élevé les équations (et le code Python) se ressemblent.

Pour expliquer cela, examinons le processus d'apprentissage de deux exemples très différents : adapter un modèle statistique et apprendre aux élèves à apprendre les mathématiques.

Scénario A : Ajuster un modèle statistique​

De manière générale, les étapes pour ajuster un modèle statistique aux données sont les suivantes :

1 Nous observons certaines données x et y. x peut être considéré comme une matrice de n. Le bruit additif est utilisé pour plus de simplicité et 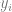est la vraie étiquette correcte. ) 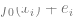2. En exécutant un algorithme d'optimisation, nous pouvons adapter le modèle 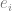aux données pour minimiser le risque empirique de 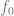. Autrement dit, nous utilisons un algorithme d'optimisation pour trouver le nombre minimisé de

, où 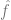est un terme de perte (capturant à quel point 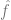est proche de y) et 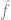est un terme de normalisation facultatif (en essayant de biaiser 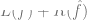vers des modèles plus simples).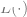

3. Nous espérons que notre modèle pourra avoir une bonne perte globale car l'erreur/perte de généralisation 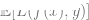est faible (cette prédiction est obtenue sur la base des données globales où se trouvent les données expérimentales).

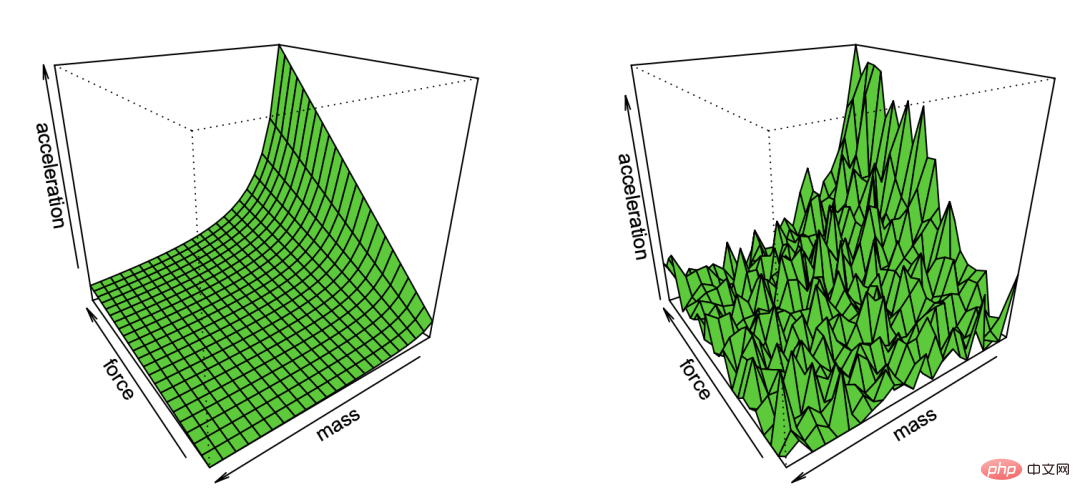
Légende : La caricature de Bradley Efron sur la première loi de Newton reproduite grâce à l'observation du bruit

Ce paradigme très général comprend de nombreux paramètres, notamment la régression linéaire des moindres carrés, les voisins les plus proches, l'entraînement des réseaux neuronaux et plus. Dans un cadre statistique classique, nous nous attendons à observer ce qui suit :

Compromis biais/variance : Prenons F comme l'ensemble des modèles optimisés. (Lorsque nous sommes dans un cadre non convexe et/ou avons un terme régularisateur, nous pouvons laisser F être l'ensemble de ces modèles qui peuvent être implémentés par l'algorithme avec une probabilité non négligeable, étant donné les effets du choix de l'algorithme et du régulariseur. ) L'écart de

F est la meilleure approximation de l'étiquette correcte et peut être obtenu par l'élément 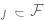. Plus la classe de F est grande, plus l'écart est petit. Lorsque 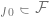, l'écart peut même être nul. Cependant, lorsque la classe F est plus grande, davantage d’échantillons sont nécessaires pour réduire sa plage d’appartenance, et donc la variance dans le modèle de sortie de l’algorithme est plus grande. L'erreur de généralisation globale est la somme du terme de biais et de la contribution à la variance.

Ainsi, l'apprentissage statistique présente souvent un compromis biais/variance et minimise l'erreur globale grâce à un « choix Boucle d'or » de complexité de modèle correcte. En fait, c'est exactement ce que font Geman et al., justifiant leur pessimisme à l'égard des réseaux de neurones en affirmant que « les limites fondamentales résultant du dilemme biais-variance s'appliquent à tous les modèles d'inférence non paramétriques, y compris les réseaux de neurones ».

Plus n'est pas toujours mieux. Dans l'apprentissage statistique, obtenir plus de fonctionnalités ou de données n'améliore pas nécessairement les performances. Par exemple, apprendre à partir de données contenant de nombreuses fonctionnalités non pertinentes est plus difficile. De même, apprendre à partir d'un modèle mixte, où les données proviennent de l'une des deux distributions (par exemple et ), est plus difficile que d'apprendre les données individuelles indépendamment.

Rendements décroissants. Dans de nombreux cas, le nombre de points de données requis pour réduire le bruit de prédiction à un certain paramètre augmente comme sous un certain paramètre k. Dans ce cas, il faut environ k échantillons pour "décoller", et une fois que vous faites cela, vous serez confronté à un système de rendements décroissants, c'est-à-dire, en supposant qu'il faut n points pour atteindre (disons) une précision de 90 %, alors vous Je veux Pour augmenter la précision à 95%, environ 3n points supplémentaires sont nécessaires. De manière générale, à mesure que les ressources augmentent (qu’il s’agisse de données, de complexité du modèle ou de calcul), nous espérons capturer des distinctions plus fines plutôt que de débloquer de nouvelles capacités qualitatives.

Forte dépendance aux pertes et aux données. Lors de l'ajustement d'un modèle à des données de grande dimension, un petit détail peut faire une grande différence dans les résultats. Les statisticiens savent que des choix tels que le régularisateur L1 ou L2 sont importants, sans compter qu'en utilisant des ensembles de données complètement différents, différents nombres d'optimiseurs de grande dimension seront extrêmement différents.

Les points de données n'ont aucune « difficulté » naturelle (du moins dans certains cas). Traditionnellement, les points de données sont échantillonnés indépendamment d'une distribution. Bien que les points proches de la limite de décision puissent être plus difficiles à classer, compte tenu de la concentration dimensionnelle des mesures, on s'attend à ce que la plupart des points aient des distances similaires. Par conséquent, au moins dans les distributions de données classiques, les niveaux de difficulté des points ne devraient pas différer grandement. Cependant, les modèles mixtes peuvent montrer différents niveaux de difficulté de cette différence, donc contrairement aux autres problèmes mentionnés ci-dessus, cette différence ne serait pas très surprenante dans un contexte statistique.

Scénario B : Apprentissage des mathématiques

Contrairement à ce qui précède, parlons de l'enseignement aux élèves de sujets mathématiques spécifiques (tels que le calcul des dérivées), en leur donnant des conseils généraux et des exercices à faire. Il ne s'agit pas d'un cadre formellement défini, mais certaines de ses caractéristiques qualitatives peuvent être considérées :

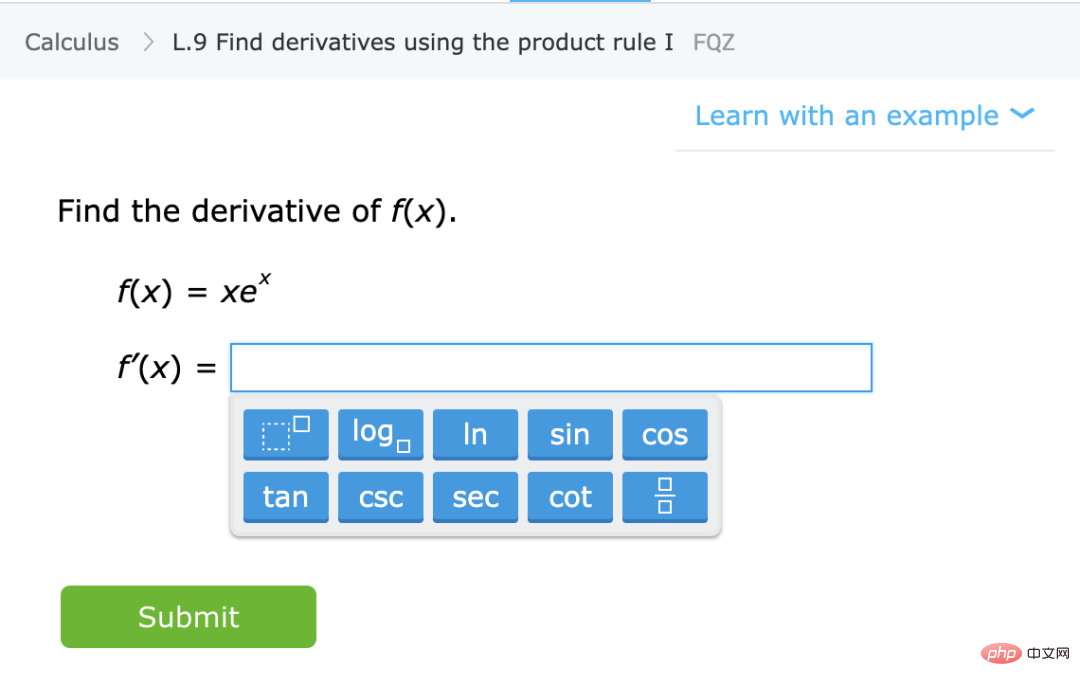
Légende : Exercices pour l'apprentissage de compétences mathématiques spécifiques du site IXL

Apprendre une compétence, pas une approximation distribution. Dans ce cas, les étudiants acquièrent une compétence plutôt qu'un estimateur/prédicteur de quantités. Bien que définir les « compétences » ne soit pas une tâche triviale, il s’agit d’un objectif qualitativement différent. En particulier, même si les exercices de cartographie des fonctions ne peuvent pas être utilisés comme une « boîte noire » pour résoudre certaines tâches liées à X, nous pensons que les représentations internes formées par les étudiants lors de la résolution de ces problèmes sont toujours utiles pour X.

Plus on est de fous, plus on est de fous. De manière générale, les étudiants obtiendront de meilleurs résultats s'ils pratiquent davantage de questions et différents types de questions. Mais en fait, le « modèle hybride » – qui consiste à résoudre des problèmes de calcul et des problèmes d’algèbre – n’affecte pas les performances des élèves en calcul et les aide réellement à apprendre.

"Explorer" ou débloquer des fonctionnalités, tournez-vous vers la représentation automatique. Bien qu'il y ait des rendements décroissants dans la résolution de problèmes à un moment donné, les étudiants semblent passer par des étapes où la résolution de problèmes aide les concepts à « cliquer » et à débloquer de nouvelles fonctionnalités. De plus, lorsque les élèves répètent un type particulier de problème, ils semblent déplacer leur capacité et leur représentation de ces problèmes à un niveau inférieur, ce qui leur permet de développer une certaine automaticité avec ces problèmes qu'ils n'avaient pas auparavant.

Les performances sont partiellement indépendantes de la perte et des données. Il existe plusieurs façons d'enseigner les concepts mathématiques, donc même si les élèves apprennent en utilisant différents livres, méthodes pédagogiques ou systèmes de notation, ils finissent toujours par apprendre le même matériel et des représentations internes similaires.

Certaines questions sont plus difficiles. Dans les exercices de mathématiques, on peut souvent constater une forte corrélation dans les méthodes utilisées par les différents élèves pour résoudre un même problème. La difficulté d'un problème semble fixe, et l'ordre de résolution des énigmes est également fixe, ce qui permet d'optimiser le processus d'apprentissage. C’est en fait ce que font des plateformes telles que IXL.

4 L'apprentissage profond s'apparente-t-il davantage à une estimation statistique ou à des techniques d'apprentissage des élèves ?

Alors, laquelle des deux métaphores ci-dessus décrit le mieux l’apprentissage profond moderne, et précisément pourquoi il connaît un tel succès ? L'ajustement du modèle statistique semble plus cohérent avec les mathématiques et le code. En fait, la boucle d'entraînement canonique de Pytorch entraîne des réseaux profonds grâce à une minimisation empirique des risques, comme décrit ci-dessus :

Cependant, à un niveau plus profond, la relation entre ces deux paramètres n'est pas si claire. Concrètement, elle peut être réalisée en réparant une tâche d'apprentissage spécifique et en utilisant la méthode « apprentissage auto-supervisé + sonde linéaire (sonde linéaire) » pour entraîner l'algorithme de classification. L'entraînement de l'algorithme est le suivant :

.

1. Supposons que les données sont une séquence 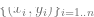, où 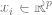est un certain point de données (comme une image spécifique) et 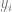est une étiquette.

2. Trouvez d'abord un réseau neuronal profond pour représenter la fonction 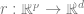Cette fonction est entraînée en utilisant uniquement des points de données 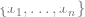sans utiliser d'étiquettes, en minimisant un certain type de fonction de perte auto-supervisée. Des exemples de telles fonctions de perte sont la reconstruction ou l'image dans l'image (récupération à partir d'une partie d'une autre entrée Lorsque l'incrément de , la relation parallèle est beaucoup plus petite que la relation parallèle entre deux points aléatoires). 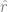3. Ensuite, nous utilisons les données étiquetées complètes 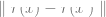pour ajuster un classificateur linéaire 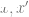(où C est le nombre de classes) afin de minimiser la perte d'entropie croisée. Le classificateur final a abouti à une cartographie de

. L'étape 3 ne convient qu'aux classificateurs linéaires, donc la « magie » se produit à l'étape 2 (apprentissage auto-supervisé des réseaux profonds). 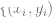Dans l'apprentissage auto-supervisé, certaines propriétés visibles incluent : 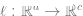Apprendre une compétence plutôt que de se rapprocher d'une fonction. 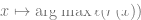L'apprentissage auto-supervisé ne consiste pas à se rapprocher d'une fonction, mais à apprendre des représentations qui peuvent être utilisées pour une variété de tâches en aval. En supposant qu'il s'agisse du paradigme dominant dans le traitement du langage naturel, le fait que les tâches en aval soient obtenues par sondage linéaire, réglage fin ou incitation est secondaire.

Plus on est de fous, plus on est de fous.

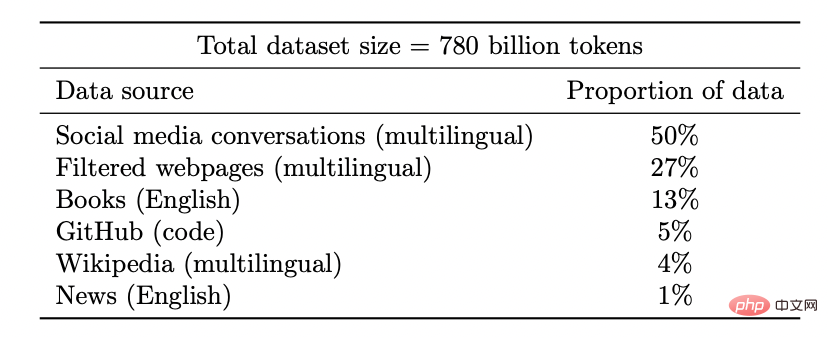
Dans l'apprentissage auto-supervisé, la qualité de la représentation s'améliore à mesure que la quantité de données augmente. Et plus les données sont diversifiées, mieux c’est.

Légende : Ensemble de données du modèle Google PaLM

Capacités de déverrouillage.

Des améliorations discontinues des modèles d'apprentissage profond sont constatées à maintes reprises à mesure que les ressources (données, calcul, taille du modèle) augmentent, et cela est également démontré dans certains environnements synthétiques.

Légende : à mesure que la taille du modèle augmente, le modèle PaLM présente des améliorations discrètes dans certains benchmarks (il n'y a que trois mises en garde concernant la taille dans la figure ci-dessus) et débloque des fonctionnalités surprenantes, telles que Expliquez la blague.

Les performances sont largement indépendantes des pertes ou des données. Plus d'une perte auto-supervisée, plusieurs pertes contrastives et reconstructives sont utilisées pour les images. Les modèles de langage emploient parfois une reconstruction unilatérale (prédisant le jeton suivant) et utilisent parfois des modèles de masquage, dont l'objectif est de prédire l'entrée masquée des jetons gauche et droit.

Il est également possible d'utiliser un ensemble de données légèrement différent, ce qui peut affecter l'efficacité, mais tant que des choix « raisonnables » sont faits, la ressource d'origine est généralement plus prédictive des performances que la perte spécifique ou l'ensemble de données utilisé.

Certaines instances sont plus difficiles que d'autres. Cela ne se limite pas à l'apprentissage auto-supervisé, les points de données peuvent avoir un certain « niveau de difficulté » inhérent.

En fait, il existe plusieurs preuves pratiques que différents algorithmes d'apprentissage ont différents "niveaux de compétence" et différents points ont différents "niveaux de difficulté" (la probabilité que le classificateur f classe correctement x, la compétence de f augmente d'un coup direction, et la difficulté de x diminue dans une direction). Le paradigme « compétence et difficulté » est l'explication la plus claire du phénomène de « précision en ligne » découvert par Recht et Miller et al., et dans l'article que j'ai co-écrit avec Kaplun, Ghosh, Garg et Nakkiran, j'ai également montré que dans l'ensemble de données Comment différentes entrées ont une « signature de difficulté » inhérente qui semble conventionnellement robuste à différents modèles.

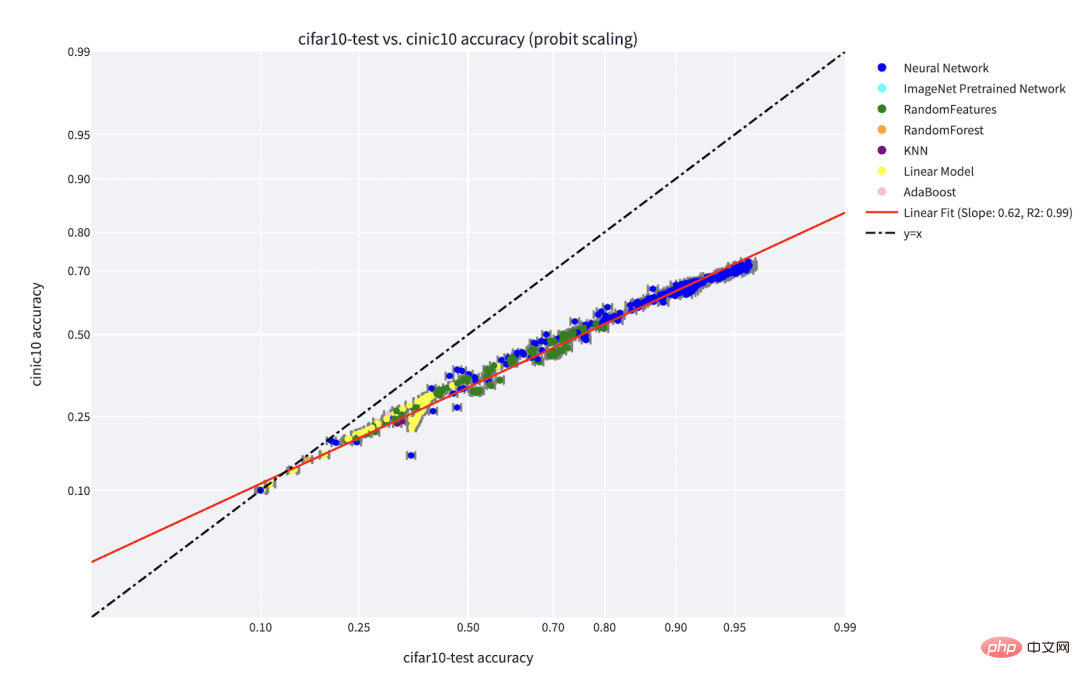
Légende : Graphique de Miller et al. montrant la précision du phénomène de ligne pour un classificateur formé sur CIFAR-10 et testé sur CINIC-10

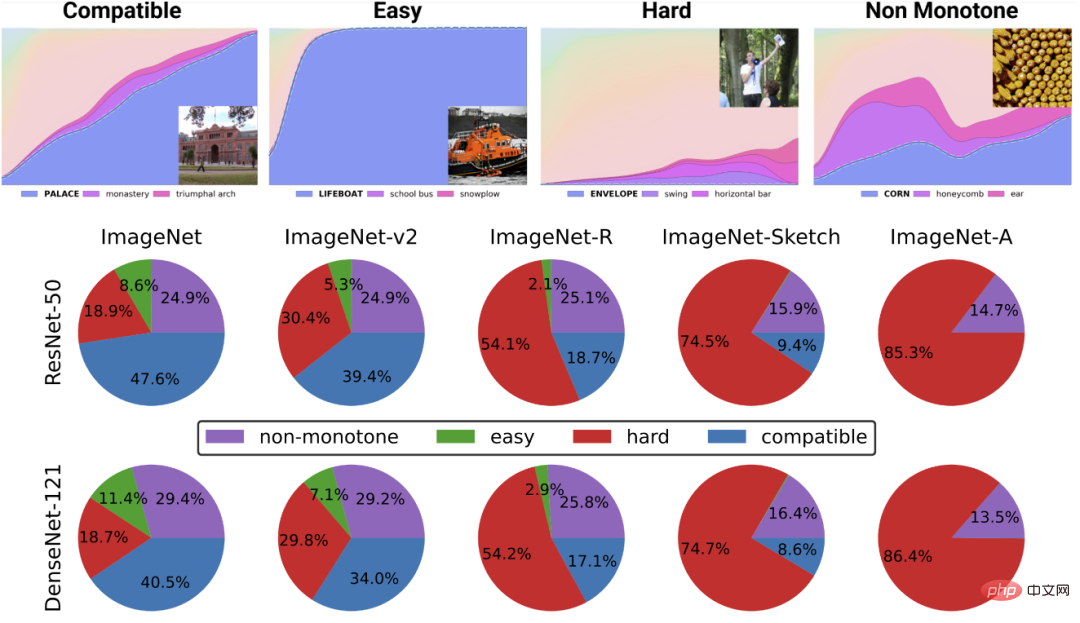
Légende : Déconstruire l'ensemble de données en différents points de « profil de difficulté » de l'article « Deconstructing Distributions: A Pointwise Framework of Learning » de Kaplun et Ghosh et al. Le graphique du haut représente différentes probabilités softmax pour la classe la plus probable en fonction de la précision globale d'un classificateur indexé par le temps de formation ; le graphique circulaire du bas montre la répartition des différents ensembles de données en différents types de points. Notamment, cette décomposition est similaire pour différentes architectures neuronales.

Former, c'est enseigner. La formation moderne de grands modèles ressemble plus à enseigner aux étudiants plutôt qu'à laisser le modèle s'adapter aux données, faire des "pauses" ou essayer d'autres méthodes lorsque les étudiants ne comprennent pas ou semblent fatigués (écart de formation). Les journaux de formation pour le grand modèle de Meta sont instructifs : en plus des problèmes matériels, on peut voir certaines interventions telles que le changement d'algorithmes d'optimisation pendant la formation, et même l'envisagement de fonctions d'activation « à chaud » (GELU vers RELU). Ce dernier point n'a pas beaucoup de sens si vous considérez la formation de modèles comme un ajustement de données plutôt que comme l'apprentissage d'une représentation.

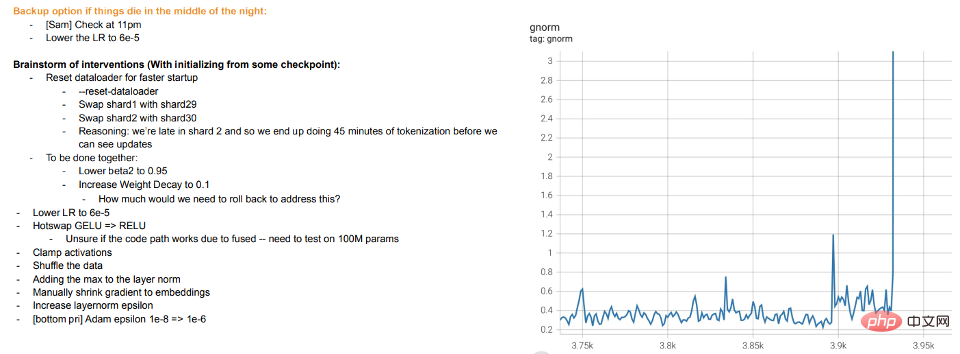
Légende : Extrait du journal d'entraînement de MetaDeux cas sont abordés ci-dessous :

Cas 1 : Apprentissage supervisé

Jusqu'à présent, nous n'avons évoqué que l'apprentissage auto-supervisé, mais le Un exemple typique d'apprentissage profond est toujours l'apprentissage supervisé. Après tout, le « moment ImageNet » de l'apprentissage profond vient d'ImageNet. Alors, ce dont nous avons discuté ci-dessus s’applique-t-il à l’apprentissage supervisé ?

Premièrement, L'émergence de l'apprentissage profond supervisé à grande échelle est, dans une certaine mesure, un accident historique, grâce à la disponibilité de grands ensembles de données étiquetés de haute qualité (c'est-à-dire ImageNet). Il est possible d’imaginer une histoire alternative : l’apprentissage profond a d’abord fait des percées dans le traitement du langage naturel grâce à l’apprentissage non supervisé, puis est ensuite passé à la vision et à l’apprentissage supervisé.

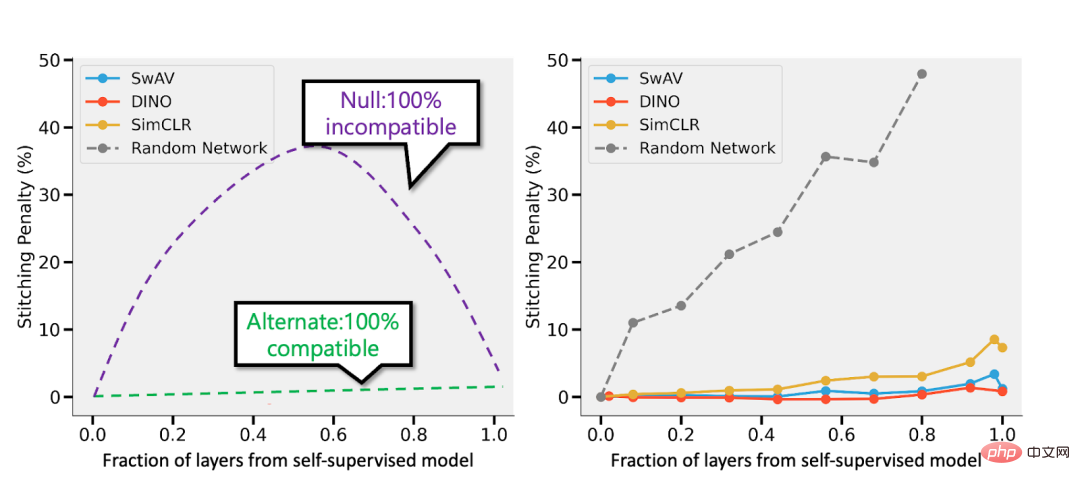
Deuxièmement, il existe des preuves que l'apprentissage supervisé se comporte de la même manière "en coulisses", même s'il utilise des fonctions de perte complètement différentes de celles de l'apprentissage auto-supervisé. Les deux atteignent généralement les mêmes performances. Il a également été découvert dans l'article "Revisiting Model Stitching to Compare Neural Representations" qu'ils ont appris des représentations internes similaires. Plus précisément, pour chaque 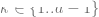, on peut "coudre" les k premières couches d'un modèle d profond entraîné avec auto-supervision avec les d-k dernières couches du modèle supervisé et garder les performances presque inchangées.

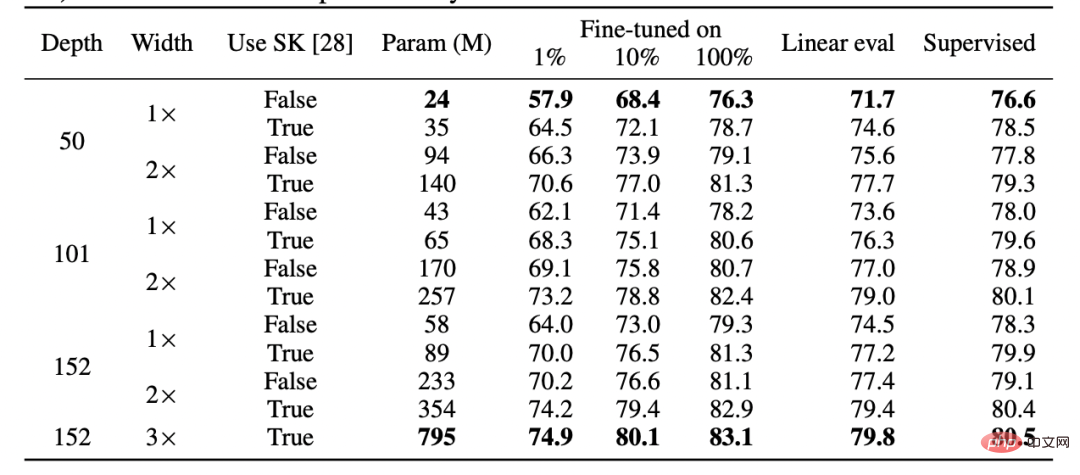
Légende : Tableau issu de l'article de l'équipe Hinton « Les grands modèles auto-supervisés sont de forts apprenants semi-supervisés ». Notez la similitude générale des performances entre l'apprentissage supervisé, le réglage fin (100%) auto-supervisé et auto-supervisé + détection linéaire " Modèles de supervision et de supervision. Gauche - Si le modèle auto-supervisé est 3 % moins précis que le modèle supervisé, alors une représentation entièrement compatible encourra une pénalité d'épissage de p 3 % (lorsque p couches proviennent du modèle auto-supervisé). Si les modèles sont complètement incompatibles, attendez-vous à ce que la précision diminue considérablement à mesure que davantage de modèles sont assemblés. À droite : résultats réels de l’épissage de différents modèles auto-supervisés.

L'avantage des modèles auto-supervisés + simples est qu'ils peuvent combiner l'apprentissage des fonctionnalités ou la "magie de l'apprentissage profond" (résultats de fonctions de représentation profonde) avec l'ajustement de modèles statistiques (effectué par des classificateurs linéaires ou autres "simples", séparés au dessus de cette représentation)

.

Enfin, bien que spéculatif, le fait que le « méta-apprentissage » semble être généralement assimilé à des représentations d'apprentissage (voir l'article « Rapid Learning or Feature Reuse ? Towards Understanding the Effectiveness of MAML » pour plus de détails), peut être considéré comme une autre preuve pour soutenir les idées de cet article, indépendamment de ce pour quoi le modèle est ostensiblement optimisé. Cas 2 : Surparamétrage Les lecteurs ont peut-être remarqué que j'ai ignoré les exemples typiques de différences entre les modèles d'apprentissage statistique et les modèles d'apprentissage profond dans les applications pratiques, à savoir l'absence de « compromis biais-variance » et sur-paramétrage L'excellente capacité de généralisation du modèle.

Il y a deux raisons pour lesquelles je ne parlerai pas de ces exemples en détail :

Premièrement, si l'apprentissage supervisé est effectivement égal à l'auto-supervision + un simple apprentissage « de niveau inférieur », alors sa capacité de généralisation peut être expliqué (pour plus de détails, veuillez consulter l'article « Pour l'apprentissage auto-supervisé, la rationalité implique une généralisation, de manière prouvable »

Deuxièmement, je pense que la sur-paramétrisation n'est pas la clé du succès de l'apprentissage en profondeur. Ce qui rend les réseaux profonds spéciaux, ce n’est pas qu’ils soient grands par rapport au nombre d’échantillons, mais qu’ils soient grands en termes absolus. En fait,

Il n'y a généralement pas de surparamétrage dans les modèles d'apprentissage non supervisés/auto-supervisés. Même pour les modèles de langage à grande échelle, ils disposent simplement d’ensembles de données plus volumineux, mais cela ne rend pas leurs performances moins mystérieuses.

Légende : Dans l'article « The Deep Bootstrap Framework : Good Online Learners are Good Offline Generalizers », les résultats des chercheurs montrent que l'architecture d'apprentissage profond actuelle est dans un état de « surparamétrage » et de « sous-échantillonnage ». les performances sont similaires (où le modèle est formé sur des données limitées pendant de nombreuses générations jusqu'à ce qu'il soit surajusté : le « monde réel » illustré ci-dessus), et également dans le cas « sous-paramétré » ou « en ligne » (où le modèle ne s'entraîne que pour une génération , et chaque échantillon n'est vu qu'une seule fois : c'est-à-dire le « monde idéal » dans l'image ci-dessus)

5 Résumé

Il ne fait aucun doute que l'apprentissage statistique joue un rôle important dans l'apprentissage profond. Cependant, si vous considérez l’apprentissage profond simplement comme un modèle qui s’adapte à plus de boutons qu’un modèle classique, vous passez à côté de nombreux facteurs qui expliquent son succès. La métaphore de ce qu’on appelle « l’étudiant humain » est encore plus inappropriée.

L'apprentissage profond est similaire à l'évolution biologique dans le sens où, bien qu'il existe de nombreuses applications répétées de la même règle (c'est-à-dire une descente de gradient avec perte d'expérience), il produit des résultats très complexes. Différents composants d'un réseau neuronal semblent apprendre différentes choses à différents moments, notamment l'apprentissage des représentations, l'ajustement prédictif, la régularisation implicite et le bruit pur. Nous cherchons toujours le bon angle pour poser des questions sur l’apprentissage profond, et encore moins pour y répondre.

Il y a un long chemin à parcourir et nous vous encouragerons ensemble.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!