Le MIT publie une version améliorée du solveur « Advanced Mathematics » : le taux de précision atteint 81 % dans 7 cours

​Non seulement elle résout les problèmes de mots mathématiques à l'école primaire, mais l'IA a également commencé à conquérir les mathématiques avancées !

Récemment, des chercheurs du MIT ont annoncé que, sur la base du modèle de pré-formation OpenAI Codex, ils ont réussi à atteindre un taux de précision de 81 % sur des problèmes de mathématiques de premier cycle grâce à un apprentissage en quelques étapes !

• Lien papier : https://arxiv.org/abs/2112.15594
• Lien code : https://github.com/idrori/mathq

Jetons un coup d'œil aux réponses à quelques petites questions d'abord, telles que Calculer le volume généré en faisant tourner le graphique d'une fonction variable unique autour d'un axe, calculer l'attracteur et la projection de Lorenz, calculer et représenter la forme géométrique de la décomposition en valeurs singulières (SVD), non seulement vous pouvez y répondre correctement , mais vous pouvez aussi donner l'explication correspondante !

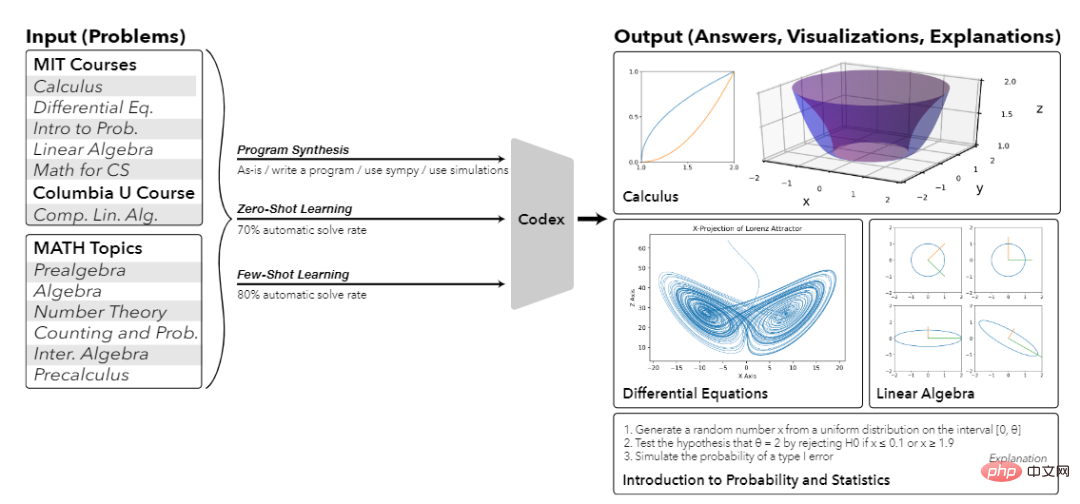
C'est vraiment incroyable. En regardant le passé, les scores élevés ont tous été dépassés. Maintenant, l'IA peut marquer 81 points d'un seul coup.

Ce qui est encore plus impressionnant, c'est qu'en plus de résoudre des problèmes difficiles à résoudre avec des modèles d'apprentissage automatique ordinaires, cette recherche montre également que cette technologie peut être promue à grande échelle et peut résoudre des problèmes dans ses cours et cours similaires.

C'est également la première fois dans l'histoire qu'un seul modèle d'apprentissage automatique peut résoudre un problème mathématique d'une telle envergure, et peut également expliquer, dessiner et même générer de nouvelles questions !

En fait, cet article a été publié dès le début de l'année. Après six mois de révision, la longueur est passée de 114 pages à 181 pages. Plus de problèmes mathématiques peuvent être résolus. Z.

Il y a quatre unités d'auteurs principales de l'article, à savoir le MIT, l'Université Columbia, l'Université Harvard et l'Université de Waterloo.

Le premier auteur, Iddo Drori, est maître de conférences au département d'IA du département de génie électrique et d'informatique du MIT et professeur associé adjoint à la School of Engineering and Applied Sciences de l'Université de Columbia. A remporté le prix du meilleur article CCAI NeurIPS 2021.

Ses principaux axes de recherche sont l'apprentissage automatique pour l'éducation, qui tente d'amener les machines à résoudre, expliquer et générer des cours de mathématiques de niveau universitaire et l'apprentissage automatique pour la science du climat, qui prédit et surveille les changements climatiques extrêmes ; sur des milliers d'années de données Climat, intégrant des travaux multidisciplinaires pour prédire les changements pluriannuels de la biogéochimie des océans dans l'océan Atlantique, des algorithmes d'apprentissage automatique pour la conduite autonome, etc.

Il est également l'auteur de The Science of Deep Learning publié par Cambridge University Press.

Jalons de l'enseignement supérieur

Avant cet article, la plupart des chercheurs pensaient que les réseaux de neurones ne pouvaient pas gérer des problèmes à nombre élevé et ne pouvaient résoudre que quelques problèmes mathématiques simples.

Même si le modèle Transformer surpasse les performances humaines dans diverses tâches de PNL, il n'est toujours pas mauvais pour résoudre des problèmes mathématiques. La raison principale est que divers grands modèles tels que GPT-3 ne sont pré-entraînés que sur des données textuelles.

Plus tard, certains chercheurs ont découvert que le modèle de langage peut toujours être guidé pour raisonner et répondre à quelques questions mathématiques simples grâce à une analyse étape par étape (chaîne de pensées), mais les problèmes mathématiques avancés ne sont pas si faciles à résoudre.

Lorsque la cible est un problème à nombre élevé, vous devez d'abord collecter une vague de données d'entraînement.

L'auteur a sélectionné au hasard 25 questions dans chacun des sept cours du MIT, dont :

• 18.01 Calcul à variable unique
• 18.02 Calcul à plusieurs variables
• 18.03 Équations différentielles
• 18.05 Introduction aux probabilités et aux statistiques
• 18.06 Al linéaire gebra
• 6.042 Mathématiques informatiques
• COMS3251 Algèbre linéaire computationnelle de l'Université de Columbia

Pour l'ensemble de données MATH, les chercheurs ont étudié les données des six sujets de l'ensemble de données (Algèbre, Comptage et Probabilités, Algèbre Intermédiaire, Théorie des Nombres, Algèbre Préliminaire ) 15 questions sélectionnées au hasard en algèbre et pré-universitaire).

Afin de vérifier que les résultats générés par le modèle ne sont pas surajustés aux données d'entraînement, les chercheurs ont choisi le cours COMS3251 qui n'a pas été publié sur Internet pour vérifier les résultats générés.

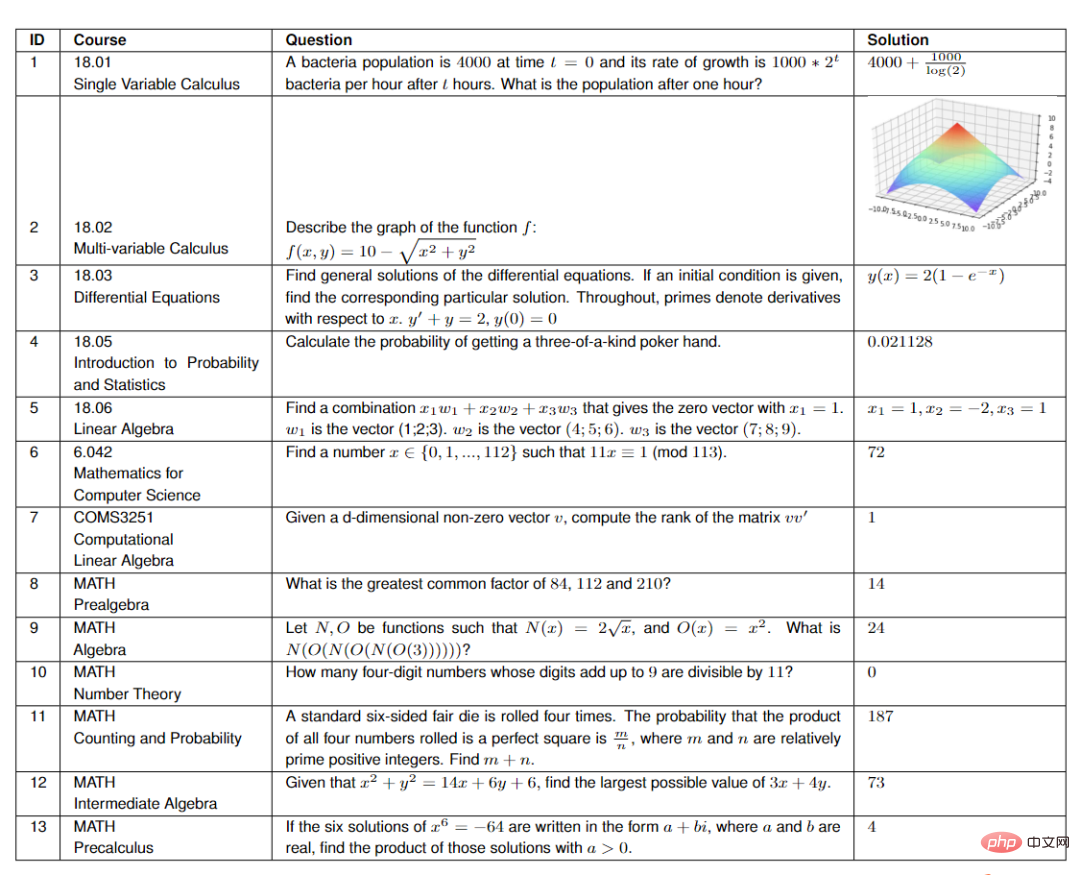
Workflow

Le modèle prend une question de cours en entrée, puis effectue une augmentation automatique avec le contexte, aboutit à un programme synthétisé et génère enfin la réponse et l'explication générée.

Pour différentes questions, les résultats de sortie peuvent être différents. Par exemple, la réponse à 18.01 est une équation, la réponse à 18.02 est une valeur booléenne, les réponses à 18.03 et 18.06 sont un graphique ou un vecteur et la réponse à 18.05. est une valeur numérique.

Lorsque vous recevez une question, la première étape consiste à laisser le modèle trouver le contexte pertinent de la question. Les chercheurs se sont principalement concentrés sur le programme Python généré par Codex, ils ont donc ajouté le texte « écrire un programme » avant la question et ont placé le texte entre trois guillemets du programme Python, faisant semblant d'être une docstring dans le programme.

Après avoir généré le programme, une invite Codex est nécessaire pour spécifier les bibliothèques à importer. L'auteur a choisi d'ajouter la chaîne "use sympy" avant la question comme contexte, spécifiant que le programme synthétisé pour résoudre le problème doit utiliser ce package.

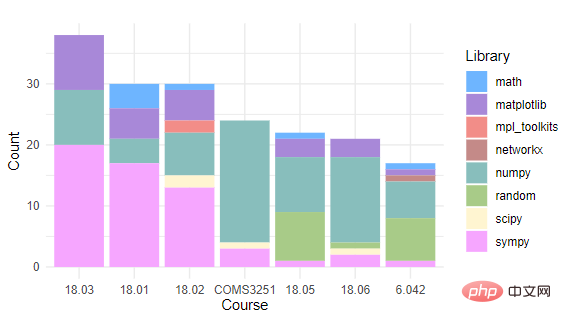
En comptant les packages de programmation Python utilisés par chaque cours, vous pouvez constater que tous les cours utilisent NumPy et Sympy. Matplotlib n'est utilisé que dans les cours comportant des problèmes nécessitant un traçage. Environ la moitié des cours utilisent les mathématiques, le hasard et SciPy. Pendant le fonctionnement réel, les chercheurs ont uniquement spécifié les packages SymPy ou liés aux dessins à importer, et les autres packages importés ont été automatiquement synthétisés.

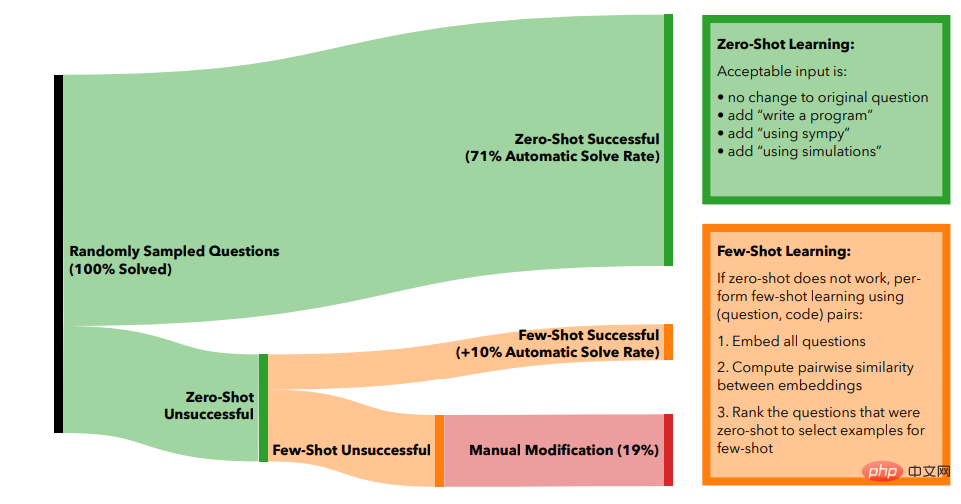
Grâce à l'apprentissage Zero-shot, c'est-à-dire que 71 % des problèmes peuvent être automatiquement résolus en utilisant uniquement l'amélioration automatique du problème d'origine.

Si un problème ne peut pas être résolu, les chercheurs essaient d'utiliser l'apprentissage en quelques étapes pour résoudre ces problèmes.

Utilisez d'abord le moteur d'intégration text-similarity-babbag-001 d'OpenAI pour obtenir l'intégration à 2048 dimensions de tous les problèmes, puis utilisez les calculs de similarité cosinus sur tous les vecteurs pour trouver les problèmes non résolus qui sont les plus similaires aux problèmes résolus. Enfin, le problème le plus similaire et son code correspondant sont utilisés comme exemples succincts du nouveau problème.

Si le code généré ne donne pas la bonne réponse, ajoutez une autre paire question-code résolue, en utilisant à chaque fois la prochaine question résolue similaire.

En pratique, on peut constater que l'utilisation de jusqu'à 5 exemples pour un apprentissage en quelques coups a le meilleur effet, et le nombre total de problèmes qui peuvent être automatiquement résolus passe de 71 % d'un apprentissage en plusieurs coups à 81 % de quelques-uns. -apprentissage par tir.

Pour résoudre les 19 % de problèmes restants, des éditeurs humains doivent intervenir.

Les chercheurs ont d'abord collecté toutes les questions et ont constaté que la plupart de ces questions étaient vagues ou contenaient des informations redondantes, telles que des références à des personnages de films ou à des événements actuels, etc. Les questions devaient être triées pour en extraire l'essence.

Le tri des questions consiste principalement à supprimer les informations redondantes, à décomposer les structures de phrases longues en composants plus petits et à convertir les invites au format de programmation.

Une autre situation qui nécessite une intervention manuelle est que la réponse à une question nécessite plusieurs étapes de dessin pour être expliquée, c'est-à-dire que le Codex doit être invité de manière interactive jusqu'à ce que l'effet de visualisation souhaité soit obtenu.

En plus de générer des réponses, le modèle devrait également être capable d'expliquer les raisons des réponses. Les chercheurs ont utilisé le mot d'invite "Voici ce que fait le code ci-dessus : 1" pour guider le modèle à générer. résultats d'explication étape par étape.

Une fois que vous avez répondu aux questions, l'étape suivante consiste à utiliser le Codex pour générer de nouvelles questions pour chaque cours.

Les chercheurs ont créé une liste numérotée de questions rédigées par les élèves de chaque classe. Cette liste a été coupée après un nombre aléatoire de questions, et les résultats ont été utilisés pour inciter le Codex à générer la question suivante.

Ce processus est répété jusqu'à ce que suffisamment de nouvelles questions aient été créées pour chaque cours.

Pour évaluer les questions générées, les chercheurs ont interrogé des étudiants du MIT qui avaient suivi ces cours ou leurs équivalents pour comparer la qualité et la difficulté des questions générées automatiquement aux cours originaux.

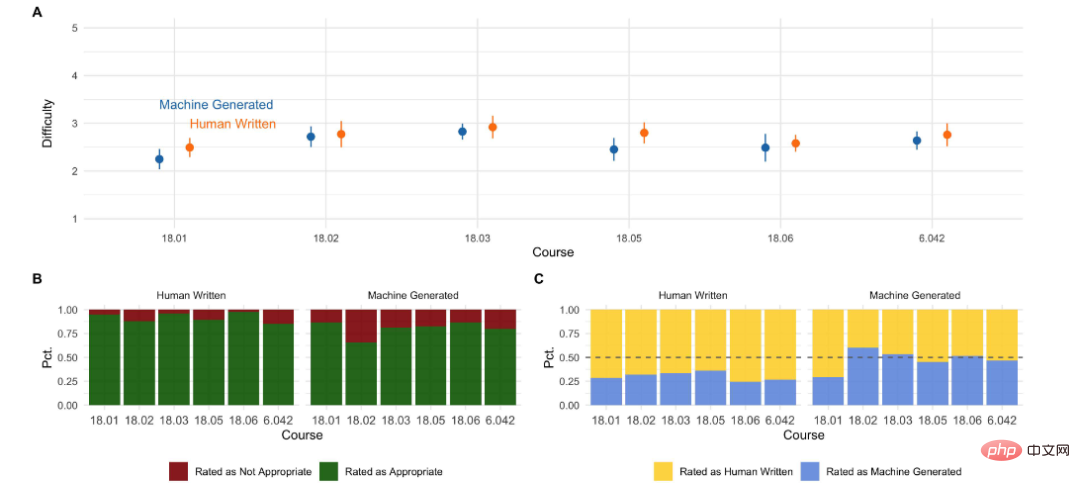
D'après les résultats de l'enquête auprès des étudiants, nous pouvons voir :

• La qualité de la notation automatique est déjà comparable à celle des questions humaines.
• En termes de difficulté, les questions humaines sont plus adaptées aux questions de cours, tandis que les résultats générés par la machine sont légèrement plus difficiles ;
• Plus de la moitié des cours ; Les étudiants peuvent voir que les questions sont générées par le modèle. Le plus proche des humains est le cours 18.01

Référence :

https://www.reddit.com/r/artificial/comments/v8liqh/researchers_built_a_neural_network_that_not_only. /​

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!