Faire évoluer l'apprentissage profond sphérique vers des données d'entrée haute résolution

Traducteur | Zhu Xianzhong

Reviewer | Sun Shujuan

Le CNN sphérique traditionnel ne peut pas être étendu aux tâches de classification haute résolution. Dans cet article, nous introduisons les couches de diffusion sphérique, un nouveau type de couche sphérique qui peut réduire la dimensionnalité des données d'entrée tout en conservant les informations pertinentes, et qui possède également des propriétés d'équivariance rotationnelle.

Les réseaux de diffusion fonctionnent en utilisant des filtres de convolution prédéfinis issus de l'analyse d'ondelettes, plutôt que d'apprendre les filtres de convolution à partir de zéro. Étant donné que les poids de la couche de diffusion sont spécifiquement conçus plutôt que appris, la couche de diffusion peut être utilisée comme étape de prétraitement unique, réduisant ainsi la résolution des données d'entrée. Notre expérience précédente montre que les CNN sphériques équipés d’une couche de diffusion initiale peuvent atteindre des résolutions de plusieurs dizaines de millions de pixels, un exploit qui était auparavant irréalisable avec les couches CNN sphériques traditionnelles.

Les méthodes traditionnelles d'apprentissage profond sphérique nécessitent des calculs

Le CNN sphérique (document 1, 2, 3) est très utile pour résoudre de nombreux types de problèmes différents en apprentissage automatique, car les sources de données de bon nombre de ces problèmes ne peuvent pas être naturellement représentées dans un avion (pour une introduction à cela, voir notre article précédent sur  : https://towardsdatascience.com/geometric-deep-learning-for-spherical-data-55612742d05f).

Une caractéristique clé des CNN sphériques est qu'ils sont équivariants à la rotation des données sphériques (dans cet article, nous nous concentrons sur les méthodes équivariantes de rotation). En pratique, cela signifie que les CNN sphériques ont des propriétés de généralisation impressionnantes, leur permettant de faire des choses comme classer les maillages d'objets 3D, quelle que soit la façon dont ils tournent (et s'ils voient le maillage lors de l'entraînement de différentes rotations).

Nous dans un récent article décrivions l'équipe Kagenova une série d'avancées développées pour améliorer l'efficacité informatique du CNN sphérique résultats ( Référence adresse : https://towardsdatascience.com/efficient-generalized-spherical-cnns-1493426362ca). La méthode que nous adoptons - CNN sphérique généralisé efficace - non seulement conserve les caractéristiques de variance égale du CNN sphérique traditionnel, mais en même temps rend le calcul plus efficace (documentation 1 ). Cependant, malgré ces progrès en matière d'efficacité informatique, les CNN sphériques sont toujours limités à des données de résolution relativement basse. Cela signifie que , CNN sphérique est actuellement ne peut pas être appliqué à des scénarios d'application passionnants qui impliquent généralement des données à plus haute résolution , tels que l'analyse de données cosmologiques et 360 pour un diplôme de réalité virtuelle en vision par ordinateur. et d'autres champs. Dans un article récemment publié, nous avons présenté le réseau de couches de diffusion sphérique pour ajuster de manière flexible le CNN sphérique général efficace pour améliorer la résolution (document 4

), dans cet article, nous passerons en revue ce contenu.

Approche hybride pour prendre en charge les données d'entrée haute résolution

En développant un CNN sphérique général efficace (Réf. 1), nous avons découvert une approche hybride très efficace pour construire une architecture CNN sphérique. Le CNN sphérique hybride peut utiliser différents styles de couches CNN sphériques dans le même réseau, permettant aux développeurs de bénéficier des avantages de différents types de couches à différentes étapes de traitement.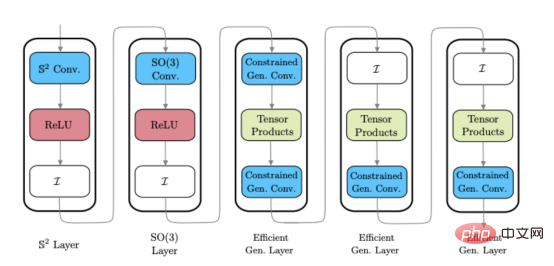

L'image ci-dessus montre un exemple d'architecture CNN sphérique hybride (veuillez noter : ces couches ne sont pas uniques, mais différents styles de couches CNN sphériques). 🎜🎜

Scattering Networks on Spheres poursuit cette approche hybride et introduit une nouvelle couche CNN sphérique qui peut être connectée aux architectures sphériques existantes. Afin d'étendre le CNN sphérique général efficace à des dimensions plus élevées, cette nouvelle couche doit avoir les caractéristiques suivantes :

1. Évolutivité avec support informatique
2. Mélange des informations aux basses fréquences pour permettre aux couches suivantes de fonctionner à basse résolution fonctionne
3. équivariance rotationnelle
4. fournit des représentations stables et localement invariantes (c'est-à-dire fournit un espace de représentation efficace)

Nous avons déterminé que la couche de réseau de diffusion a le potentiel de satisfaire toutes ces caractéristiques énumérées ci-dessus.

Réseaux de diffusion sur la sphère

Les réseaux de diffusion proposés pour la première fois par Mallat (Réf. 5) dans un contexte euclidien peuvent être considérés comme des CNN avec des filtres convolutionnels fixes dérivés de l'analyse d'ondelettes exportées. Les réseaux de diffusion se sont révélés très utiles pour la vision par ordinateur traditionnelle (euclidienne), en particulier lorsque les données sont limitées – où l'apprentissage des filtres convolutifs est difficile. Ensuite, nous discutons brièvement du fonctionnement interne des couches de réseau de diffusion, de la manière dont elles répondent aux exigences définies dans la section précédente et de la manière dont elles peuvent être développées pour l'analyse de données sphériques.

Le traitement des données au sein de la couche de diffusion est effectué par trois opérations de base. Le premier élément constitutif est la convolution d’ondelettes fixe, qui est similaire à la convolution d’apprentissage normale utilisée dans le CNN euclidien. Après convolution des ondelettes, le réseau de diffusion applique une approche modulaire non linéaire à la représentation résultante. Enfin, la diffusion utilise une fonction de mise à l'échelle qui exécute un algorithme de moyenne locale présentant certaines similitudes avec les couches de pooling des CNN ordinaires. L'application répétée de ces trois éléments constitutifs disperse les données d'entrée dans un arbre informatique et extrait la représentation résultante (similaire à un canal CNN) de l'arbre à différentes étapes du traitement. Un schéma simplifié de ces opérations est présenté ci-dessous.

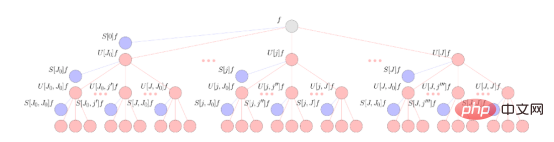
Cette figure illustre le réseau de diffusion sphérique du signal sphérique f. Le signal se propage via une transformée en ondelettes sphériques en cascade combinée à une fonction d'activation en valeur absolue représentée par des nœuds rouges. La sortie du réseau de diffusion est obtenue en projetant ces signaux sur une fonction de mise à l'échelle des ondelettes sphériques, ce qui donne les coefficients de diffusion représentés par des nœuds bleus.

Du point de vue traditionnel du deep learning, le fonctionnement des réseaux décentralisés semble un peu obscur. Cependant, chaque opération de calcul décrite a un objectif spécifique : celui d’exploiter les résultats théoriques fiables de l’analyse par ondelettes.

Les convolutions d'ondelettes dans les réseaux de diffusion sont soigneusement dérivées pour extraire des informations pertinentes à partir des données d'entrée. Par exemple, pour les images naturelles, les ondelettes sont définies pour extraire spécifiquement des informations relatives aux contours à hautes fréquences et aux formes générales des objets à basses fréquences. Par conséquent, dans un environnement planaire, les filtres de réseau de diffusion peuvent présenter certaines similitudes avec les filtres CNN traditionnels. Il en va de même pour le réglage sphérique, où nous utilisons des ondelettes discrétisées à l'échelle (voir Réf. 4 pour plus de détails).

Étant donné que le filtre d'ondelettes est fixe, la couche de diffusion initiale ne doit être appliquée qu'une seule fois et n'a pas besoin d'être appliquée à plusieurs reprises tout au long du processus de formation (comme la couche initiale du CNN traditionnel). Cela rend le réseau de diffusion évolutif sur le plan informatique, répondant aux exigences de la fonctionnalité 1 ci-dessus. De plus, la couche de diffusion réduit la dimensionnalité de ses données d'entrée, ce qui signifie que seul un espace de stockage limité doit être utilisé pour mettre en cache la représentation de diffusion lors de la formation des couches CNN en aval.

La méthode non linéaire du module est utilisée derrière la convolution des ondelettes. Premièrement, cela injecte des caractéristiques non linéaires dans les couches du réseau neuronal. Deuxièmement, l'opération de module mélange les informations haute fréquence du signal d'entrée avec les données basse fréquence pour répondre à l'exigence 2 ci-dessus. La figure ci-dessous montre la distribution de fréquence de la représentation en ondelettes des données avant et après le calcul non linéaire du module.

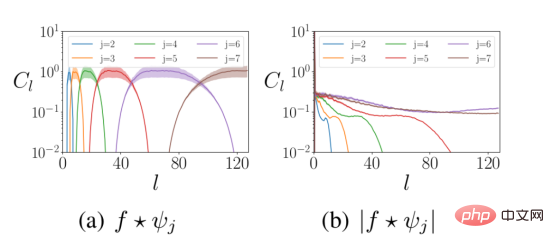
La figure ci-dessus montre la distribution des coefficients d'ondelettes à différentes fréquences sphériques l avant et après le fonctionnement modulaire. L'énergie du signal d'entrée se déplace des hautes fréquences (panneau de gauche) vers les basses fréquences (panneau de droite). où f est le signal d'entrée et Ψ représente l'ondelette de mise à l'échelle j.

Après avoir appliqué le calcul du module, projetez le signal résultant sur la fonction de mise à l'échelle. La fonction de mise à l'échelle extrait les informations basse fréquence des résultats de la représentation, de manière similaire à l'opération de fonction de pooling dans CNN traditionnel.

Nous avons testé empiriquement les propriétés théoriques d'égalité de variance des réseaux de diffusion sphérique. Le test est effectué en faisant tourner le signal et en l'alimentant à travers le réseau de diffusion, puis en comparant la représentation résultante à la représentation résultante des données d'entrée après avoir traversé le réseau de diffusion, puis en effectuant le calcul de rotation. Il peut être démontré à partir des données du tableau ci-dessous que l'erreur d'égalité de variance pour une profondeur donnée est faible, répondant ainsi à l'exigence 3 ci-dessus (généralement en pratique, la profondeur d'un trajet ne dépassera pas la profondeur de deux trajets, car la plupart des l'énergie du signal a déjà été capturée).

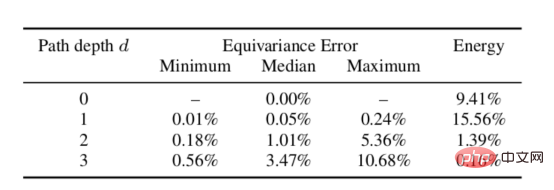
Erreur de variance égale de rotation du réseau de diffusion sphérique à différentes profondeurs

Enfin, il est théoriquement prouvé que le réseau de diffusion euclidienne est stable aux petites différentielles ou distorsions (Littérature 5 ). Actuellement, ce résultat a été étendu aux réseaux de diffusion sur des variétés riemanniennes compactes (document 6), notamment aux environnements sphériques (document 4). En pratique, la stabilité à la morphologie des disparités signifie que la représentation calculée par le réseau de diffusion ne différera pas de manière significative si l'entrée est légèrement modifiée (voir notre article précédent pour une discussion sur le rôle de la stabilité dans l'apprentissage profond géométrique , L'adresse est https://towardsdatascience.com/a-brief-introduction-to-geometric-deep-learning-dae114923ddb). Ainsi, les réseaux de diffusion fournissent un espace de représentation bien exécuté sur lequel l'apprentissage ultérieur peut être effectué efficacement, satisfaisant l'exigence 4 ci-dessus.

CNN sphérique évolutif et équivariant en rotation

Considérant que les couches de diffusion introduites satisfont toutes nos propriétés souhaitées, nous sommes ensuite prêts à les intégrer dans notre CNN sphérique hybride. Comme mentionné précédemment, la couche de diffusion peut être fixée sur l'architecture existante en tant qu'étape de pré-traitement initiale afin de réduire la taille de la représentation pour le traitement ultérieur de la couche sphérique.

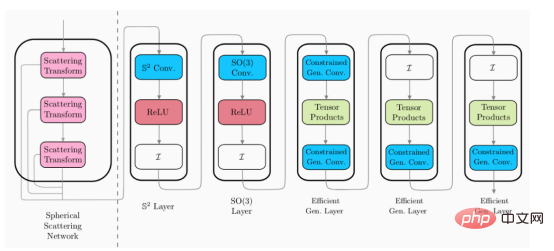
Dans l'image ci-dessus, le module de couche de diffusion (à gauche de la ligne pointillée) est une couche de conception. Cela signifie qu'il ne nécessite pas de formation, tandis que les couches restantes (à droite de la ligne pointillée) peuvent être entraînées. Par conséquent, cela signifie que les couches de diffusion peuvent être appliquées comme étape de prétraitement unique pour réduire la dimensionnalité des données d'entrée.

Étant donné que les réseaux de dispersion ont une représentation fixe d'une entrée donnée, les couches de réseau de dispersion peuvent être appliquées une fois à l'ensemble de données au début de l'entraînement, et la représentation de faible dimension résultante est mise en cache pour entraîner les couches suivantes. Heureusement, les représentations dispersées ont une dimensionnalité réduite, ce qui signifie que l'espace disque requis pour les stocker est relativement faible. Grâce à l’existence de cette nouvelle couche de diffusion sphérique, le CNN sphérique généralisé efficace peut être étendu aux problèmes de classification à haute résolution.

Classification de l'anisotropie du fond cosmique des micro-ondes

Comment la matière est-elle distribuée dans l'univers ? Il s’agit d’une question de recherche fondamentale pour les cosmologistes et a des implications significatives pour les modèles théoriques de l’origine et de l’évolution de notre univers. Le fond diffus cosmologique (CMB) – l’énergie résiduelle du Big Bang – cartographie la répartition de la matière dans l’univers. Les cosmologues observent le CMB sur la sphère céleste, ce qui nécessite des méthodes informatiques permettant une analyse cosmologique au sein de la sphère céleste.

Les cosmologues sont très intéressés par les méthodes d'analyse du fond diffus cosmologique, car ces méthodes peuvent détecter des propriétés non gaussiennes dans la répartition du fond diffus cosmologique dans l'espace, ce qui a des implications importantes pour les théories de l'univers primitif. Cette approche analytique doit également pouvoir s’adapter à une résolution astronomique. Nous démontrons que notre réseau de diffusion répond à ces exigences en classant les simulations CMB comme gaussiennes ou non gaussiennes avec une résolution de L = 1024. Le réseau de diffusion a réussi à classer ces simulations avec une précision de 95,3 %, ce qui est bien meilleur que les 53,1 % obtenus par le CNN sphérique traditionnel à basse résolution.

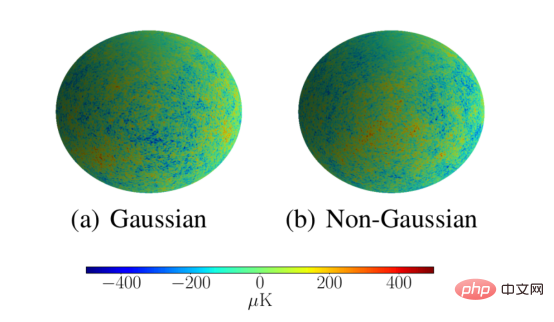
La figure ci-dessus donne des exemples de simulation à haute résolution de CMB gaussiens et non gaussiens pour évaluer la capacité des réseaux de diffusion sphérique à s'adapter à des résolutions élevées.

Résumé

Dans cet article, nous avons exploré la capacité des couches de diffusion sphériques à compresser la dimensionnalité de leurs représentations d'entrée tout en préservant les informations importantes pour les tâches en aval. Nous avons montré que cela rend les couches de diffusion très utiles pour les tâches de classification de sphères à haute résolution. Cela ouvre la porte à des applications potentielles auparavant insolubles, telles que l’analyse de données cosmologiques et la classification d’images/vidéos haute résolution à 360°. Cependant, de nombreux problèmes de vision par ordinateur, tels que la segmentation ou l’estimation de la profondeur, qui nécessitent des prédictions denses, nécessitent à la fois une sortie et une entrée de grande dimension. Enfin, comment développer des couches CNN sphériques contrôlables qui peuvent augmenter la dimensionnalité de la représentation de sortie tout en conservant une variance égale est un sujet de recherche actuel des développeurs de Kagenova. Ceux-ci seront abordés dans le prochain article.

Références

［1］Cobb, Wallis, Mavor-Parker, Marignier, Price, d'Avezac, McEwen, CNN sphériques généralisés efficaces, ICLR (2021), arXiv:2010.11661

［2］ , Geiger, Koehler, Welling, CNN sphériques, ICLR (2018), arXiv:1801.10130

［3］ Esteves, Allen-Blanchette, Makadia, Daniilidis, Learning SO(3) Représentations équivariantes avec des CNN sphériques, ECCV (2018) , arXiv : 1711.06721

[4] McEwen, Jason, Wallis, Christopher et Mavor-Parker, Augustine N., Réseaux de diffusion sur la sphère pour les CNN sphériques évolutifs et équivariants en rotation, ICLR (2022), arXiv : 2102.02828

［5］ Bruna, Joan et Stéphane Mallat, Réseaux de convolution à diffusion invariante, IEEE Transaction on Pattern Analysis and Machine Intelligence (2013)

［6］ Perlmutter, Michael et al., Réseaux de diffusion d'ondelettes géométriques sur riemannien compact collecteurs, Mathematical and Scientific Machine Learning PMLR (2020), arXiv:1905.10448

Introduction du traducteur

Zhu Xianzhong, rédacteur en chef de la communauté 51CTO, blogueur expert 51CTO, conférencier, professeur d'informatique dans une université de Weifang, vétéran du secteur indépendant. pièces de l’industrie de la programmation.

Titre original : ​​Scaling Spherical Deep Learning to High-Resolution Input Data​​, auteur : Jason McEwen, Augustine Mavor-Parker

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!