Maison >développement back-end >Tutoriel Python >Comprendre le clustering hiérarchique dans un seul article (code Python)
Comprendre le clustering hiérarchique dans un seul article (code Python)
- 王林avant
- 2023-04-11 21:13:082029parcourir

Tout d'abord, le clustering appartient à l'apprentissage non supervisé de l'apprentissage automatique, et il existe de nombreuses méthodes, comme les célèbres K-means. Le clustering hiérarchique est également un type de clustering et est également très couramment utilisé. Ensuite, je passerai brièvement en revue les principes de base des K-means, puis présenterai lentement la définition et les étapes hiérarchiques du clustering hiérarchique, qui seront plus utiles à comprendre pour tout le monde.
Quelle est la différence entre le clustering hiérarchique et les K-means ?
Le principe de fonctionnement des K-means peut être brièvement résumé comme suit :
- Déterminer le nombre de clusters (k)
- Sélectionner aléatoirement k points dans les données comme centroïdes
- Attribuer tous les points au centroïde de cluster le plus proche
- Calculer le nouveau formation Le centroïde du cluster
- Répétez les étapes 3 et 4
Il s'agit d'un processus itératif jusqu'à ce que le centroïde du cluster nouvellement formé ne change pas ou que le nombre maximum d'itérations soit atteint.
Mais K-means présente certaines lacunes. Nous devons décider du nombre de clusters K avant le démarrage de l'algorithme. Mais en réalité, nous ne savons pas combien de clusters il devrait y avoir, nous en définissons donc généralement un en fonction de notre propre compréhension. ce qui peut conduire à certains écarts entre notre compréhension et la situation réelle.
Le clustering hiérarchique est complètement différent. Il ne nous oblige pas à spécifier le nombre de clusters au début. Au lieu de cela, une fois que l'ensemble du clustering hiérarchique est complètement formé, le nombre correspondant de clusters et de clusters peut être trouvé automatiquement en déterminant la distance appropriée. .
Qu'est-ce que le clustering hiérarchique ?
Ci-dessous, nous présenterons ce qu'est le clustering hiérarchique, du superficiel au profond, en commençant par un exemple simple.
Supposons que nous ayons les points suivants et que nous souhaitions les regrouper :

Nous pouvons attribuer chacun de ces points à un cluster distinct, soit 4 clusters (4 couleurs) :

Ensuite, en fonction du similarité (distance) de ces clusters, les points les plus similaires (les plus proches) sont regroupés et le processus est répété jusqu'à ce qu'il ne reste qu'un seul cluster :
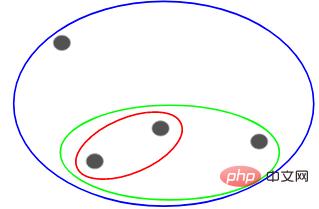
Ce qui précède consiste essentiellement à construire une structure hiérarchique. Comprenons cela d’abord, et nous présenterons ses étapes de superposition en détail plus tard.
Types de clustering hiérarchique
Il existe principalement deux types de clustering hiérarchique :
- Clustering hiérarchique aggloméré
- Clustering hiérarchique divisé
Cluster hiérarchique agglomératif
Prenons d'abord tous les points pour devenir des clusters séparés. Les clusters sont ensuite continuellement combinés par similarité. jusqu'à ce qu'il n'y ait qu'un seul cluster au final. C'est le processus de clustering hiérarchique agglomératif, qui est cohérent avec ce que nous venons de dire plus haut.
Cluster hiérarchique divisé
Le clustering hiérarchique fractionné est tout le contraire. Il commence à partir d'un seul cluster et le divise progressivement jusqu'à ce qu'il ne puisse pas être divisé, c'est-à-dire que chaque point est un cluster.
Donc, peu importe qu'il s'agisse de 10, 100, 1000 points de données, ces points appartiennent tous au même cluster au début :
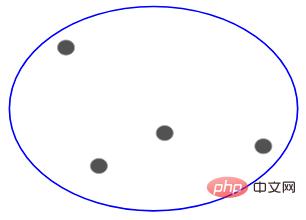
Maintenant, à chaque itération, divisez les deux points du cluster les plus éloignés, et répétez ce processus jusqu'à ce que chaque cluster ne contienne qu'un seul point :

Le processus ci-dessus est un clustering hiérarchique divisé.
Étapes pour effectuer un clustering hiérarchique
Le processus général de clustering hiérarchique a été décrit ci-dessus Vient maintenant le point clé : Comment déterminer la similarité entre les points ?
C'est l'un des problèmes les plus importants du clustering. La méthode générale de calcul de similarité consiste à calculer la distance entre les centroïdes de ces clusters. Les points avec une distance minimale sont appelés points similaires et nous pouvons les fusionner ou appeler cela un algorithme basé sur la distance.
Également dans le clustering hiérarchique, il existe un concept appelé matrice de proximité, qui stocke la distance entre chaque point. Ci-dessous, nous utilisons un exemple pour comprendre comment calculer la similarité, la matrice de proximité et les étapes spécifiques du clustering hiérarchique.
Introduction au cas
Supposons qu'un enseignant souhaite diviser les élèves en différents groupes. J'ai maintenant les scores de chaque élève sur le devoir et je souhaite les diviser en groupes en fonction de ces scores. Il n’y a pas d’objectif fixe ici quant au nombre de groupes à former. Puisque l’enseignant ne sait pas quel type d’élèves doit être affecté à quel groupe, ce problème ne peut pas être résolu comme un problème d’apprentissage supervisé. Ci-dessous, nous essaierons d'appliquer un regroupement hiérarchique pour séparer les étudiants en différents groupes.
Voici les résultats de 5 étudiants :
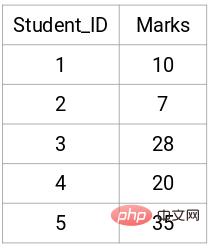
Créer une matrice de proximité
Tout d'abord, nous devons créer une matrice de proximité, qui stocke la distance entre chaque point, afin que nous puissions obtenir une matrice carrée de forme n X n.
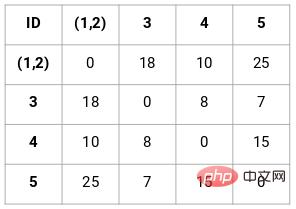
Dans ce cas, la matrice de proximité 5 x 5 suivante peut être obtenue :
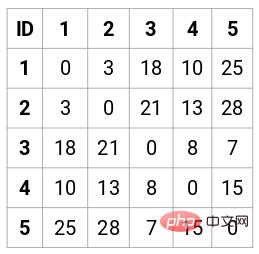
Il y a deux points à noter dans la matrice :
- Les éléments diagonaux de la matrice sont toujours 0, car la distance entre un le point et lui-même est toujours 0
- Utilisez la formule de distance euclidienne pour calculer la distance des éléments non diagonaux
Par exemple, si nous voulons calculer la distance entre les points 1 et 2, la formule de calcul est :
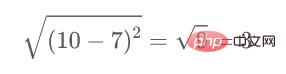
De même, calculez-le comme suit Une fois la méthode terminée, les éléments restants de la matrice de proximité sont remplis.
Effectuer un clustering hiérarchique
Ceci est implémenté à l'aide d'un clustering hiérarchique agglomératif.
Étape 1 : Tout d'abord, nous attribuons tous les points dans un seul cluster :

Ici, différentes couleurs représentent différents clusters, 5 points dans nos données, c'est-à-dire qu'il y a 5 clusters différents.
Étape 2 : Ensuite, nous devons trouver la distance minimale dans la matrice de proximité et fusionner les points avec la plus petite distance. Ensuite, nous mettons à jour la matrice de proximité :
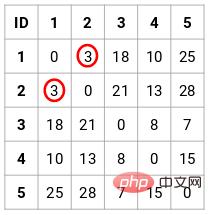
La distance minimale est de 3, nous allons donc fusionner les points 1 et 2 :
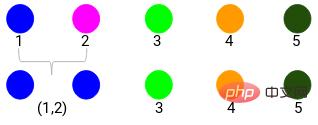
Voyons les clusters mis à jour et mettons à jour la matrice de proximité en conséquence :
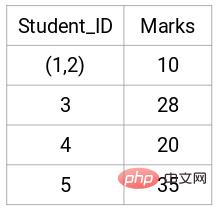
Mise à jour Après cela, nous avons pris la plus grande valeur (7, 10) entre les points 1 et 2 pour remplacer la valeur de ce cluster. Bien entendu, en plus de la valeur maximale, on peut également prendre la valeur minimale ou moyenne. Nous calculerons ensuite à nouveau la matrice de proximité de ces clusters :
Étape 3 : Répétez l'étape 2 jusqu'à ce qu'il ne reste qu'un seul cluster.
Après avoir répété toutes les étapes, nous obtiendrons les clusters fusionnés comme indiqué ci-dessous :
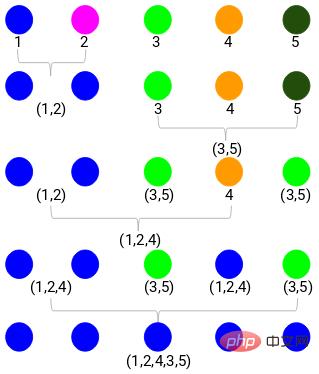
C'est ainsi que fonctionne le clustering hiérarchique agglomératif. Mais le problème est que nous ne savons toujours pas en combien de groupes diviser ? Est-ce le groupe 2, 3 ou 4 ?
Commençons par comment choisir le nombre de clusters.
Comment choisir le nombre de clusters ?
Pour obtenir le nombre de clusters pour le clustering hiérarchique, nous utilisons un concept appelé dendrogramme.
Grâce au dendrogramme, nous pouvons sélectionner plus facilement le nombre de grappes.
Retour à l'exemple ci-dessus. Lorsque nous fusionnons deux clusters, le dendrogramme enregistre en conséquence la distance entre ces clusters et la représente graphiquement. Voici l'état d'origine du dendrogramme. L'abscisse enregistre la marque de chaque point, et l'axe vertical enregistre la distance entre les points :
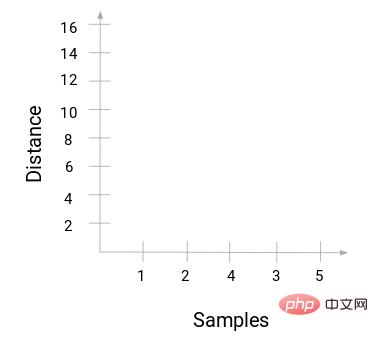
Lors de la fusion de deux clusters, le dendrogramme apparaîtra Une fois connecté, la hauteur du dendrogramme. la connexion est la distance entre les points. Voici le processus de clustering hiérarchique que nous venons d'effectuer.
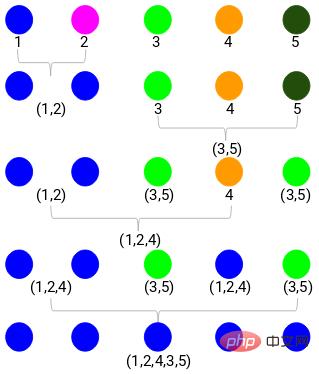
Ensuite, commencez à dessiner un diagramme arborescent du processus ci-dessus. En partant de la fusion des échantillons 1 et 2, la distance entre ces deux échantillons est de 3.
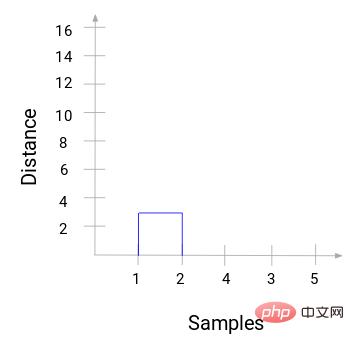
Vous pouvez voir que 1 et 2 ont été fusionnés. La ligne verticale représente la distance entre 1 et 2. De la même manière, toutes les étapes de fusion des clusters sont tracées selon le processus de clustering hiérarchique, et finalement un dendrogramme comme celui-ci est obtenu :
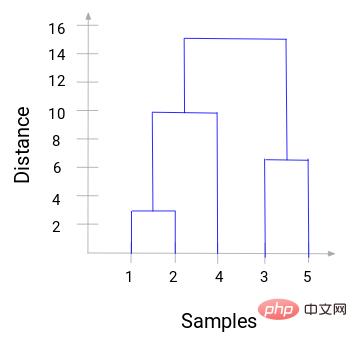
Grâce au dendrogramme, nous pouvons visualiser clairement les étapes du regroupement hiérarchique. Plus les lignes verticales du dendrogramme sont éloignées, plus la distance entre les grappes est grande.
Avec ce dendrogramme, il nous est beaucoup plus facile de déterminer le nombre de grappes.
Maintenant, nous pouvons définir une distance seuil et tracer une ligne horizontale. Par exemple, nous fixons le seuil à 12 et traçons une ligne horizontale comme suit :
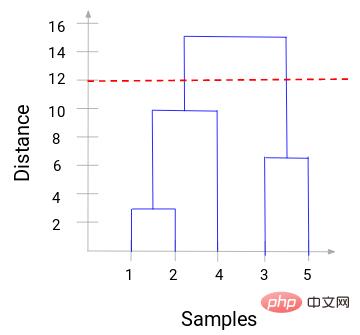
Comme vous pouvez le voir sur les points d'intersection, le nombre de clusters est le nombre d'intersections avec la ligne horizontale et la ligne verticale du seuil (la la ligne rouge coupe 2 lignes verticales, nous aurons 2 clusters). Correspondant à l'abscisse, un cluster aura un ensemble d'échantillons (1,2,4) et l'autre cluster aura un ensemble d'échantillons (3,5).
De cette façon, nous résolvons le problème de la détermination du nombre de clusters dans un clustering hiérarchique via un dendrogramme.
Cas pratique du code Python
Ce qui précède est la base théorique, et toute personne ayant des bases mathématiques peut la comprendre. Voici comment implémenter ce processus à l'aide du code Python. Voici des données de segmentation client à afficher.
L'ensemble de données et le code se trouvent dans mon référentiel GitHub :
https://github.com/xiaoyusmd/PythonDataScience
Si vous le trouvez utile, donnez-lui une étoile !
Ces données proviennent de la bibliothèque d'apprentissage automatique UCI. Notre objectif est de segmenter les clients des grossistes-distributeurs en fonction de leurs dépenses annuelles sur différentes catégories de produits telles que le lait, les produits d'épicerie, les régions, etc.
Commencez par standardiser les données pour rendre toutes les données de la même dimension faciles à calculer, puis appliquez un clustering hiérarchique pour segmenter les clients.
from sklearn.preprocessing import normalize
data_scaled = normalize(data)
data_scaled = pd.DataFrame(data_scaled, columns=data.columns)
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))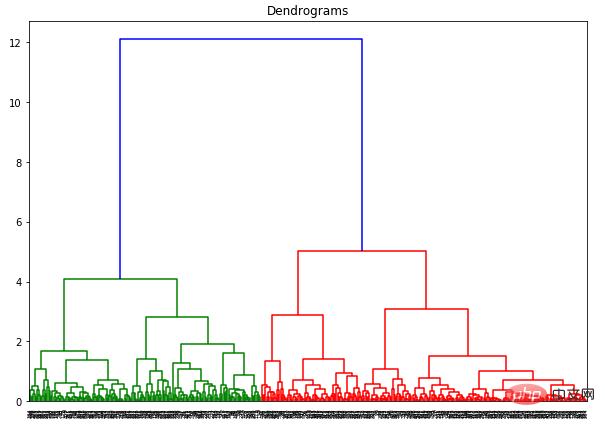
L'axe des x contient tous les échantillons et l'axe des y représente la distance entre ces échantillons. La ligne verticale avec la plus grande distance est la ligne bleue Supposons que nous décidions de couper le dendrogramme avec un seuil de 6 :
plt.figure(figsize=(10, 7))
plt.title("Dendrograms")
dend = shc.dendrogram(shc.linkage(data_scaled, method='ward'))
plt.axhline(y=6, color='r', linestyle='--')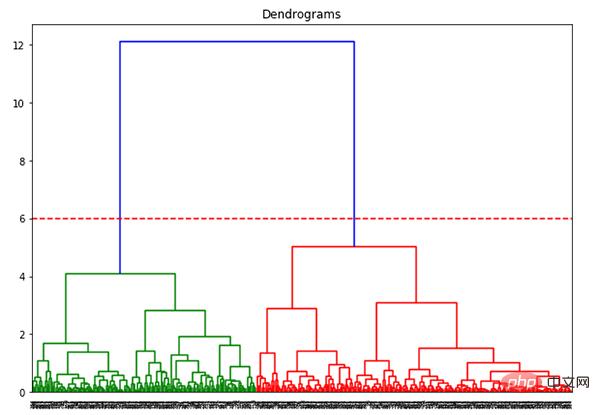
Maintenant que nous avons deux clusters, nous voulons appliquer un clustering hiérarchique à ces 2 clusters :
from sklearn.cluster import AgglomerativeClustering cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward') cluster.fit_predict(data_scaled)

Depuis que nous avons défini 2 clusters, nous pouvons voir les valeurs de 0 et 1 dans la sortie. 0 représente les points appartenant au premier cluster et 1 représente les points appartenant au deuxième cluster.
plt.figure(figsize=(10, 7)) plt.scatter(data_scaled['Milk'], data_scaled['Grocery'], c=cluster.labels_)
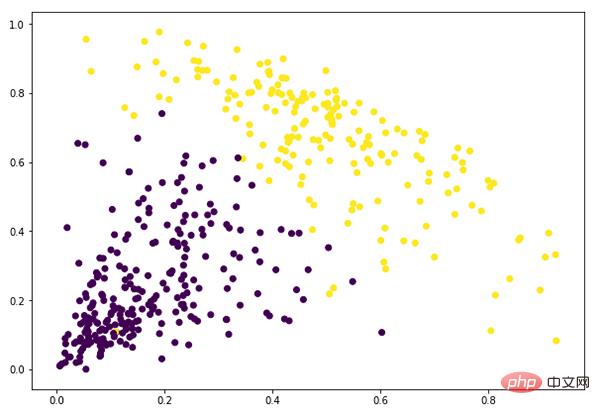
À ce stade, nous avons terminé avec succès le clustering.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

