Le transport optimal et son application à l'équité

​Traducteur | Li Rui

Critique | Sun Shujuan

Le transport optimal est né de l'économie et est maintenant développé comme un outil permettant d'allouer au mieux les ressources. Les origines de la théorie du transport optimal remontent à 1781, lorsque le scientifique français Gaspard Monge étudia une méthode censée « déplacer la terre » et construire des fortifications pour l'armée de Napoléon. Dans l’ensemble, le transport optimal est le problème de savoir comment déplacer toutes les ressources (comme le minerai de fer) d’un ensemble d’origines (mines) vers un ensemble de destinations (usines sidérurgiques) tout en minimisant la distance totale que les ressources doivent parcourir. Mathématiquement, les chercheurs voulaient trouver une fonction qui mappe chaque origine vers une destination tout en minimisant la distance totale entre l'origine et sa destination correspondante. Malgré sa description anodine, les progrès sur la conception originale du problème, connue sous le nom de conception de Munger, sont restés au point mort pendant près de 200 ans.

Dans les années 1940, le mathématicien soviétique Leonid Kantorovitch a adapté la formulation du problème en une version moderne, aujourd'hui connue sous le nom de théorie de Monge Kantorov, qui constituait le premier pas vers une solution. La nouveauté ici est qu'une partie du minerai de fer provenant d'une même mine peut être fournie à différentes aciéries. Par exemple, 60 % du minerai de fer d’une mine peut être fourni à une aciérie, tandis que les 40 % restants du minerai de fer de la mine peuvent être fournis à une autre aciérie. Mathématiquement, il ne s'agit plus d'une fonction, car la même origine correspond désormais à des destinations potentiellement multiples. En revanche, c'est ce qu'on appelle le couplage entre la distribution d'origine et la distribution de destination, comme le montre la figure ci-dessous ; en sélectionnant une mine dans la distribution bleue (origine) et en se déplaçant verticalement le long de la figure, on montre où le minerai de fer est envoyé. Distribution de aciéries (destination).

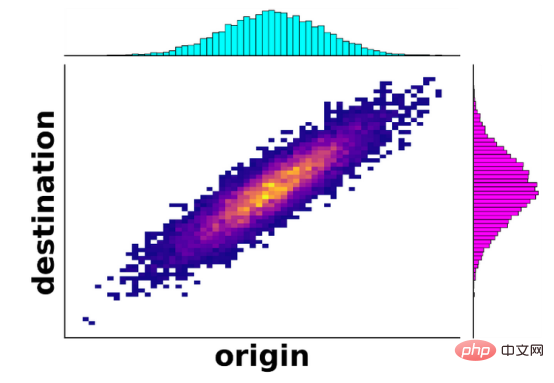
Dans le cadre de ce nouveau développement, Kantorivich a introduit un concept important appelé distance de Wasserstein. Semblable à la distance entre deux points sur une carte, la distance de Wasserstein (également connue sous le nom de distance du bulldozer inspirée de son scénario original) mesure la distance entre deux distributions, comme les distributions bleue et magenta dans ce cas. Si toutes les mines de fer sont éloignées de toutes les usines de fer, alors la distance de Wasserstein entre la répartition (emplacement) des mines et la répartition des aciéries sera grande. Même avec ces nouvelles améliorations, on ne sait toujours pas s’il existe réellement un meilleur moyen de transporter les ressources en minerai de fer, et encore moins quelle méthode. Finalement, dans les années 1990, la théorie a commencé à se développer rapidement à mesure que les progrès de l’analyse mathématique et de l’optimisation conduisaient à des solutions partielles au problème. Au XXIe siècle, le transport optimal a commencé à s’étendre à d’autres domaines, tels que la physique des particules, la dynamique des fluides, voire même les statistiques et l’apprentissage automatique.

Le transport optimal dans les temps modernes

Avec l'explosion de nouvelles théories, le transport optimal est devenu le centre de nombreux nouveaux algorithmes statistiques et d'intelligence artificielle au cours des deux dernières décennies. Dans presque tous les algorithmes statistiques, les données sont modélisées, explicitement ou implicitement, comme ayant une distribution de probabilité sous-jacente. Par exemple, si des données sur le revenu individuel sont collectées dans différents pays, il y aura une distribution de probabilité du revenu de cette population dans chaque pays. Si vous souhaitez comparer deux pays en fonction de la répartition des revenus de leur population, vous avez besoin d'un moyen de mesurer l'écart entre les deux répartitions. C’est exactement pourquoi l’optimisation des transports (en particulier la distance de Wasserstein) devient si utile en science des données. Cependant, la distance de Wasserstein n’est pas la seule mesure de la distance entre deux distributions de probabilité. En fait, en raison de leur lien avec la physique et la théorie de l’information, les deux options de distance L-2 et de divergence Kullback-Leibler (KL) ont été historiquement plus courantes. Le principal avantage de la distance de Wasserstein par rapport à ces alternatives est qu'elle prend en compte à la fois les valeurs et leurs probabilités lors du calcul de la distance, alors que la distance L-2 et la divergence KL ne prennent en compte que les probabilités. L'image ci-dessous montre un exemple d'un ensemble de données artificielles sur les revenus de trois pays fictifs.

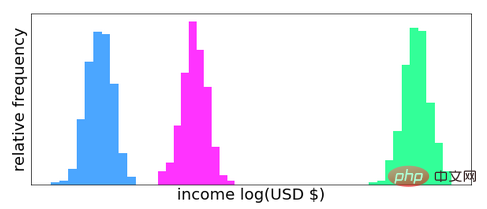
Dans ce cas, puisque les distributions ne se chevauchent pas, la distance L-2 (ou divergence KL) entre les distributions bleue et magenta sera approximativement la même que la distance L-2 entre les distributions bleue et verte. . En revanche, la distance de Wasserstein entre les distributions bleue et magenta sera bien plus petite que la distance de Wasserstein entre les distributions bleue et verte car il y a une différence significative entre les valeurs (séparation horizontale). Cette propriété de la distance de Wasserstein la rend idéale pour quantifier les différences entre les distributions, en particulier les différences entre les ensembles de données.

Parvenir à l'équité grâce à des transports optimaux

Avec de grandes quantités de données collectées chaque jour, l'apprentissage automatique devient de plus en plus courant dans de nombreux secteurs, et les data scientists doivent être de plus en plus prudents pour ne pas permettre à leurs analyses et algorithmes de perpétuer des phénomènes dans le données. Certains écarts et écarts deviennent permanents. Par exemple, si un ensemble de données sur l’approbation d’un prêt hypothécaire contient des informations sur la race des candidats, mais que les minorités ont été victimes de discrimination lors du processus de collecte en raison des méthodes utilisées ou de préjugés inconscients, alors un modèle formé sur ces données reflétera l’écart sous-jacent.

L'optimisation des expéditions peut aider à atténuer ce biais et à améliorer l'équité de deux manières. La première et la plus simple méthode consiste à utiliser la distance de Wasserstein pour déterminer s’il existe un biais potentiel dans l’ensemble de données. Par exemple, on peut estimer la distance de Wasserstein entre la répartition des montants de prêts approuvés pour les femmes et la répartition des montants de prêts approuvés pour les hommes. Si la distance de Wasserstein est très grande, c’est-à-dire statistiquement significative, alors un biais potentiel peut être suspecté. Cette idée de tester s'il existe une différence entre deux groupes est connue en statistique sous le nom de test d'hypothèse à deux échantillons.

Alternativement, l'expédition optimale peut même être utilisée pour renforcer l'équité dans le modèle lorsque l'ensemble de données sous-jacent lui-même est biaisé. Ceci est utile d’un point de vue pratique, car de nombreux ensembles de données du monde réel présentent un certain degré de biais, et la collecte de données impartiales peut être très coûteuse, prendre beaucoup de temps ou être irréalisable. Il est donc plus pratique d’utiliser les données existantes, aussi imparfaites soient-elles, et d’essayer de garantir que le modèle atténue ce biais. Ceci est accompli en appliquant une contrainte dans le modèle appelée parité démographique forte, qui oblige les prédictions du modèle à être statistiquement indépendantes de tout attribut sensible. Une approche consiste à mapper la distribution des prédictions du modèle à la distribution des prédictions ajustées qui ne dépendent pas d'attributs sensibles. Cependant, l'ajustement des prédictions modifie également les performances et la précision du modèle, il existe donc un compromis entre les performances du modèle et la mesure dans laquelle le modèle s'appuie sur des attributs sensibles (c'est-à-dire l'équité).

Assurez des performances optimales du modèle en modifiant le moins possible les prédictions, tout en garantissant que les nouvelles prédictions sont indépendantes des attributs sensibles, ce qui entraîne une expédition optimale. La nouvelle distribution prédite par ce modèle ajusté s'appelle le centroïde de Wasserstein et a fait l'objet de nombreuses recherches au cours de la dernière décennie. Le centre de gravité de Wasserstein est similaire à la moyenne d'une distribution de probabilité dans le sens où il minimise la distance totale qui le sépare de toutes les autres distributions. L'image ci-dessous montre trois distributions (verte, bleue et magenta) ainsi que leurs centres de gravité de Wasserstein (rouge).

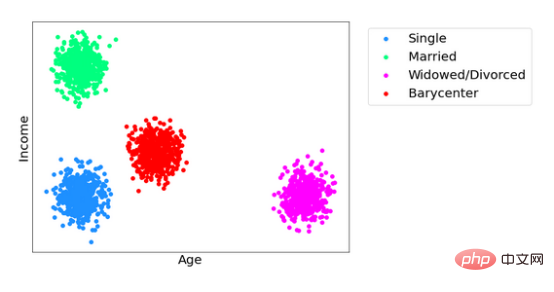
Dans l'exemple ci-dessus, supposons qu'un modèle soit construit pour prédire l'âge et le revenu d'une personne sur la base d'un ensemble de données contenant un attribut sensible (tel que l'état civil), qui peut prendre trois valeurs possibles : célibataire (bleu), marié (vert) et veuf/divorcé (magenta). Le nuage de points montre la distribution des prédictions du modèle pour chaque valeur différente. Mais si l'on souhaite ajuster ces valeurs pour que les prédictions du nouveau modèle soient aveugles à l'état matrimonial d'une personne, chacune de ces distributions peut être mappée au centre de gravité en rouge en utilisant un transport optimal. Étant donné que toutes les valeurs correspondent à la même distribution, on ne peut plus juger de l'état civil d'une personne en fonction du revenu et de l'âge, ou vice versa. Le centre de gravité préserve au maximum la fidélité du modèle.

L'omniprésence croissante des modèles de données et d'apprentissage automatique utilisés dans la prise de décision des entreprises et des gouvernements a conduit à l'émergence de nouvelles questions sociales et éthiques sur la manière de garantir l'application équitable de ces modèles. De nombreux ensembles de données contiennent une sorte de biais en raison de la nature de la manière dont ils sont collectés. Il est donc important que les modèles formés sur eux n'exacerbent pas ce biais ou toute discrimination historique. Le transport optimal n’est qu’un moyen de résoudre ce problème qui s’est aggravé ces dernières années. De nos jours, il existe des moyens rapides et efficaces de calculer des cartes et des distances de transport optimales, ce qui rend cette approche adaptée aux grands ensembles de données modernes. Alors que les gens s’appuient de plus en plus sur des modèles et des informations basés sur des données, l’équité a été et continuera d’être une question centrale dans la science des données, et un transport optimal jouera un rôle clé dans la réalisation de cet objectif.

Titre original : ​​Le transport optimal et ses applications à l'équité​​​, auteur : Terrence Alsup​

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!