Présentation de l'intégration de graphiques : méthodes d'intégration de nœuds, de bords et de graphiques et implémentation de Python

L'apprentissage automatique basé sur les graphiques a fait de grands progrès ces dernières années. Les méthodes basées sur des graphes ont des applications dans de nombreux problèmes courants en science des données, tels que la prédiction de liens, la découverte de communautés, la classification de nœuds, etc. Il existe de nombreuses façons de résoudre un problème en fonction de la manière dont vous l’organisez et des données dont vous disposez. Cet article fournira un aperçu de haut niveau des algorithmes d'intégration basés sur des graphiques. Enfin, nous présenterons également comment utiliser les bibliothèques Python (telles que node2vec) pour générer diverses intégrations sur des graphiques.

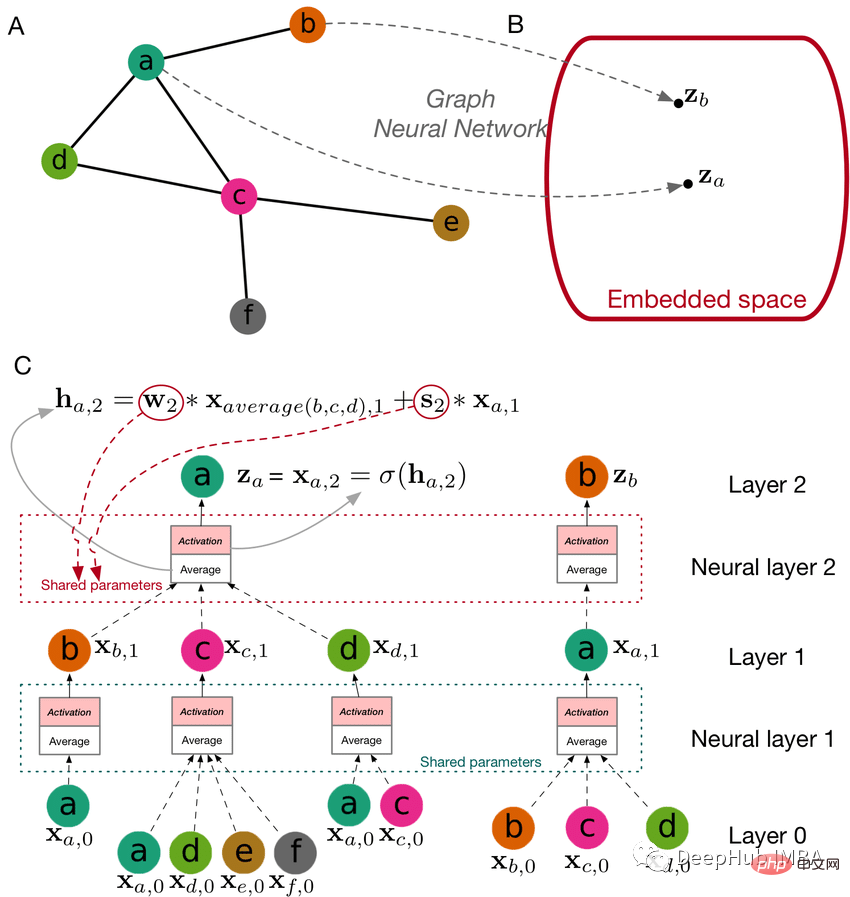
Apprentissage automatique basé sur des graphiques

L'intelligence artificielle a diverses branches, depuis les systèmes de recommandation, les séries chronologiques, le traitement du langage naturel, la vision par ordinateur, l'apprentissage automatique des graphiques, etc. Il existe plusieurs façons de résoudre les problèmes courants liés à l’apprentissage automatique basé sur des graphiques. Y compris la découverte de communauté, la prédiction de liens, la classification des nœuds, etc.

Un problème majeur avec l'apprentissage automatique des graphes est de trouver un moyen de représenter (ou d'encoder) la structure du graphe afin que les modèles d'apprentissage automatique puissent facilement l'exploiter [1]. Généralement, pour résoudre ce problème en apprentissage automatique, il faut apprendre une sorte de représentation via des données tabulaires structurées associées au modèle, ce qui était auparavant effectué via des mesures statistiques ou des fonctions de noyau. Ces dernières années, la tendance a été au codage de graphiques pour générer des vecteurs d'intégration pour la formation de modèles d'apprentissage automatique.

L'objectif des modèles d'apprentissage automatique est d'entraîner les machines à apprendre et à reconnaître des formes dans des ensembles de données à grande échelle. Ceci est amplifié lorsque vous travaillez avec des graphiques, car ceux-ci fournissent des structures différentes et complexes que d'autres formes de données (telles que le texte, l'audio ou les images) n'ont pas. L'apprentissage automatique basé sur des graphiques peut détecter et expliquer des modèles sous-jacents récurrents [2].

Nous pourrions être intéressés par la détermination des informations démographiques liées aux utilisateurs des réseaux sociaux. Les données démographiques incluent l'âge, le sexe, la race, etc. Les réseaux sociaux d’entreprises comme Facebook ou Twitter comptent des millions, voire des milliards d’utilisateurs et des milliards de côtés. Il y aura certainement plusieurs modèles liés aux données démographiques des utilisateurs de ce réseau qui ne seront pas facilement détectables par les humains ou les algorithmes, mais le modèle devrait être capable de les apprendre. De même, nous souhaiterions peut-être recommander à deux utilisateurs de devenir amis, mais ils ne le sont pas encore. Cela fournit du matériel pour la prédiction de liens, une autre application de l’apprentissage automatique basé sur des graphiques.

Qu'est-ce que l'intégration d'images ?

L'ingénierie des fonctionnalités fait référence à la méthode courante de traitement des données d'entrée pour former un ensemble de fonctionnalités qui fournissent une représentation compacte et significative de l'ensemble de données d'origine. Les résultats de la phase d’ingénierie des fonctionnalités serviront de contribution au modèle d’apprentissage automatique. Il s'agit d'un processus nécessaire lorsque l'on travaille avec des ensembles de données structurés tabulaires, mais c'est une approche difficile à mettre en œuvre lorsque l'on travaille avec des données graphiques, car il faut trouver un moyen de générer une représentation appropriée associée à toutes les données graphiques.

Il existe de nombreuses façons de générer des caractéristiques représentant des informations structurelles à partir de graphiques. La méthode la plus courante et la plus simple consiste à extraire des statistiques à partir d’un graphique. Cela peut inclure la distribution de la reconnaissance, le classement des pages, les mesures de centralité, le score Jaccard, etc. Les attributs requis sont ensuite incorporés dans le modèle via une fonction noyau, mais le problème avec les fonctions noyau est que la complexité temporelle associée à la génération des résultats est élevée.

Les tendances de recherche récentes se sont tournées vers la recherche de représentations graphiques significatives et la génération de représentations intégrées pour les graphiques. Ces intégrations apprennent des représentations graphiques qui préservent la structure originale du réseau. On peut le considérer comme une fonction de cartographie conçue pour transformer un graphe discret en un domaine continu. Une fois qu'une fonction est apprise, elle peut être appliquée à un graphique et le mappage résultant peut être utilisé comme ensemble de fonctionnalités pour les algorithmes d'apprentissage automatique.

Types d'intégration de graphiques

L'analyse des graphiques peut être décomposée en 3 niveaux de granularité. Niveau nœud, niveau bord et niveau graphique (graphique entier). Chaque niveau consiste en un processus différent qui génère des vecteurs d'intégration, et le processus choisi doit dépendre du problème et des données traitées. Chaque intégration de niveau de granularité présentée ci-dessous est accompagnée de diagrammes pour les distinguer visuellement les uns des autres.

Incorporations de nœuds

Au niveau du nœud, un vecteur d'intégration associé à chaque nœud du graphique est généré. Ce vecteur d'intégration peut s'adapter à la représentation et à la structure du graphique. Essentiellement, les nœuds proches les uns des autres doivent également avoir des vecteurs proches les uns des autres. C'est l'un des principes de base des modèles d'intégration de nœuds populaires tels que Node2Vec.

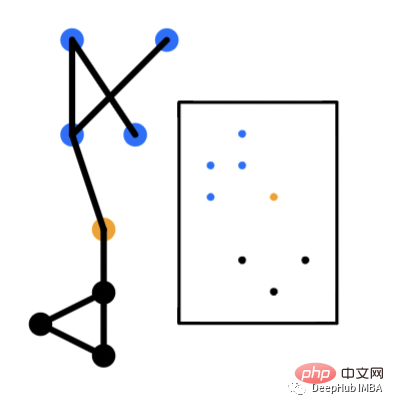
Edge Embedding

Dans la couche Edge, un vecteur d'intégration est généré en fonction de chaque arête du graphique. Le problème de prédiction de lien est une application courante utilisant l’intégration de bords. La prédiction de lien fait référence à la prédiction de la probabilité qu'un bord connecte une paire de nœuds. Ces intégrations peuvent apprendre les propriétés de bord fournies par le graphique. Par exemple, dans un graphique de réseau social, vous pouvez avoir un graphique à plusieurs arêtes dans lequel les nœuds peuvent être connectés par des arêtes en fonction de la tranche d'âge, du sexe, etc. Ces propriétés de bord peuvent être apprises en représentant le vecteur de corrélation du bord.

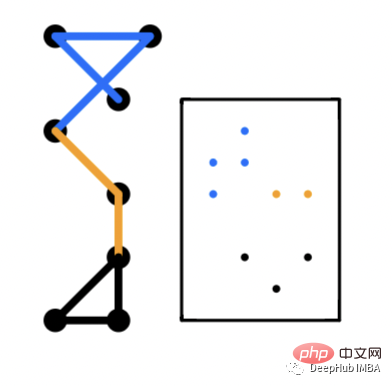
Incorporations de graphiques

Les intégrations au niveau du graphique sont rares, elles consistent à générer un vecteur d'intégration représentant chaque graphique. Par exemple, dans un grand graphique comportant plusieurs sous-graphes, chaque sous-graphe correspondant possède un vecteur d'incorporation qui représente la structure du graphe. Les problèmes de classification sont une application courante dans laquelle les intégrations de graphiques peuvent être utiles. Ces types de problèmes impliqueront de classer les graphiques dans des catégories spécifiques.

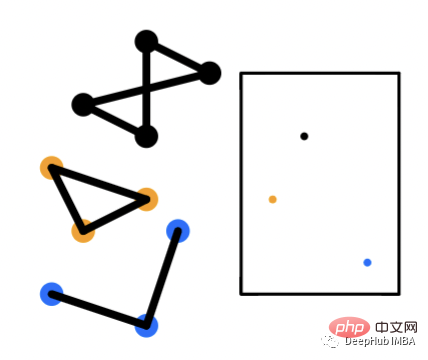
Implémentation Python

Utilisez le code Python pour implémenter les bibliothèques suivantes dont nous avons besoin

Pythnotallow=3.9
 networkx>=2.5
 pandas>=1.2.4
 numpy>=1.20.1
 node2vec>=0.4.4
 karateclub>=1.3.3
 matplotlib>=3.3.4

Si vous n'avez pas installé le package node2vec, veuillez vous référer à sa documentation. L'installation du package karateclub est similaire à

Incorporation de nœuds

import random
 import networkx as nx
 import matplotlib.pyplot as plt
 
 from node2vec import Node2Vec
 from node2vec.edges import HadamardEmbedder
 from karateclub import Graph2Vec
 
 plt.style.use("seaborn")
 
 # generate barbell network
 G = nx.barbell_graph(
m1 = 13,
m2 = 7
 )
 
 # node embeddings
 def run_n2v(G, dimensions=64, walk_length=80, num_walks=10, p=1, q=1, window=10):
"""
Given a graph G, this method will run the Node2Vec algorithm trained with the
appropriate parameters passed in.
 
Args:
G (Graph) : The network you want to run node2vec on
 
Returns:
This method will return a model
 
Example:
G = np.barbell_graph(m1=5, m2=3)
mdl = run_n2v(G)
"""
 
mdl = Node2Vec(
G,
dimensions=dimensions,
walk_length=walk_length,
num_walks=num_walks,
p=p,
q=q
)
mdl = mdl.fit(window=window)
return mdl
 
 mdl = run_n2v(G)
 
 # visualize node embeddings
 x_coord = [mdl.wv.get_vector(str(x))[0] for x in G.nodes()]
 y_coord = [mdl.wv.get_vector(str(x))[1] for x in G.nodes()]
 
 plt.clf()
 plt.scatter(x_coord, y_coord)
 plt.xlabel("Dimension 1")
 plt.ylabel("Dimension 2")
 plt.title("2 Dimensional Representation of Node2Vec Algorithm on Barbell Network")
 plt.show()

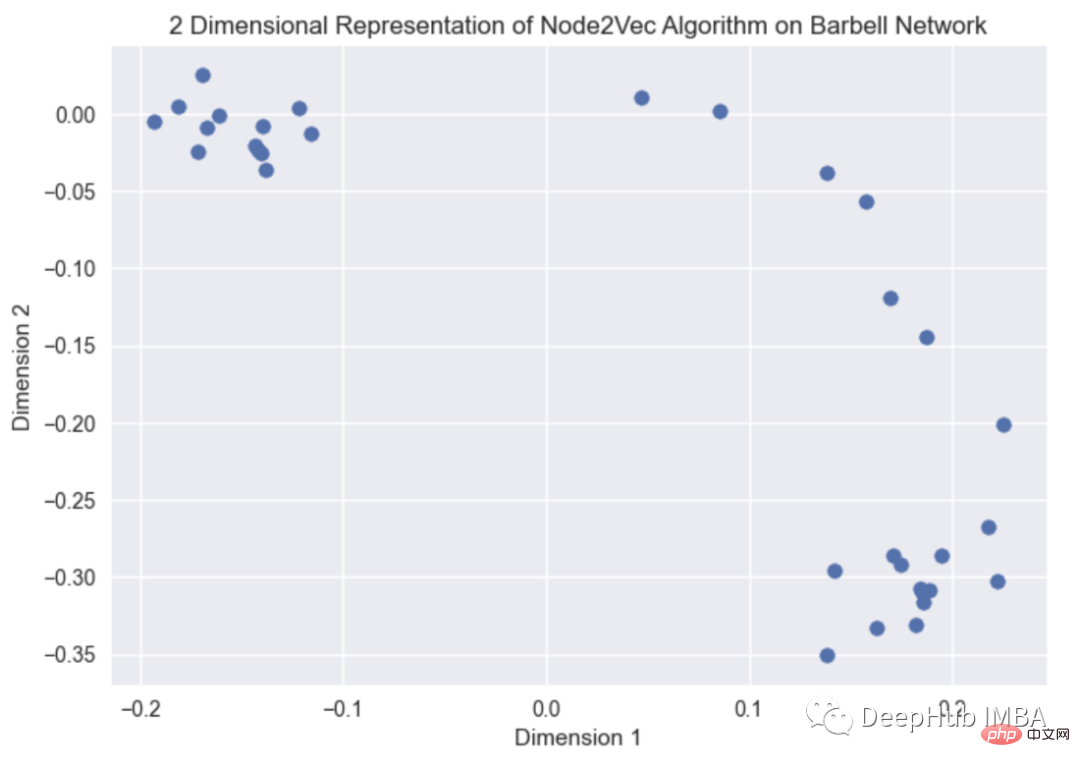
L'image ci-dessus est une intégration visuelle de nœuds générée par un graphique d'haltères. Il existe de nombreuses méthodes pour calculer l'intégration de nœuds, telles que node2vec, la marche profonde, les marches aléatoires. , etc. node2vec est utilisé ici.

Edge Embedding

edges_embs = HadamardEmbedder(
keyed_vectors=mdl.wv
 )
 
 # visualize embeddings
 coordinates = [
edges_embs[(str(x[0]), str(x[1]))] for x in G.edges()
 ]
 
 plt.clf()
 plt.scatter(coordinates[0], coordinates[1])
 plt.xlabel("Dimension 1")
 plt.ylabel("Dimension 2")
 plt.title("2 Dimensional Representation of Edge Embeddings on Barbell Network")
 plt.show()

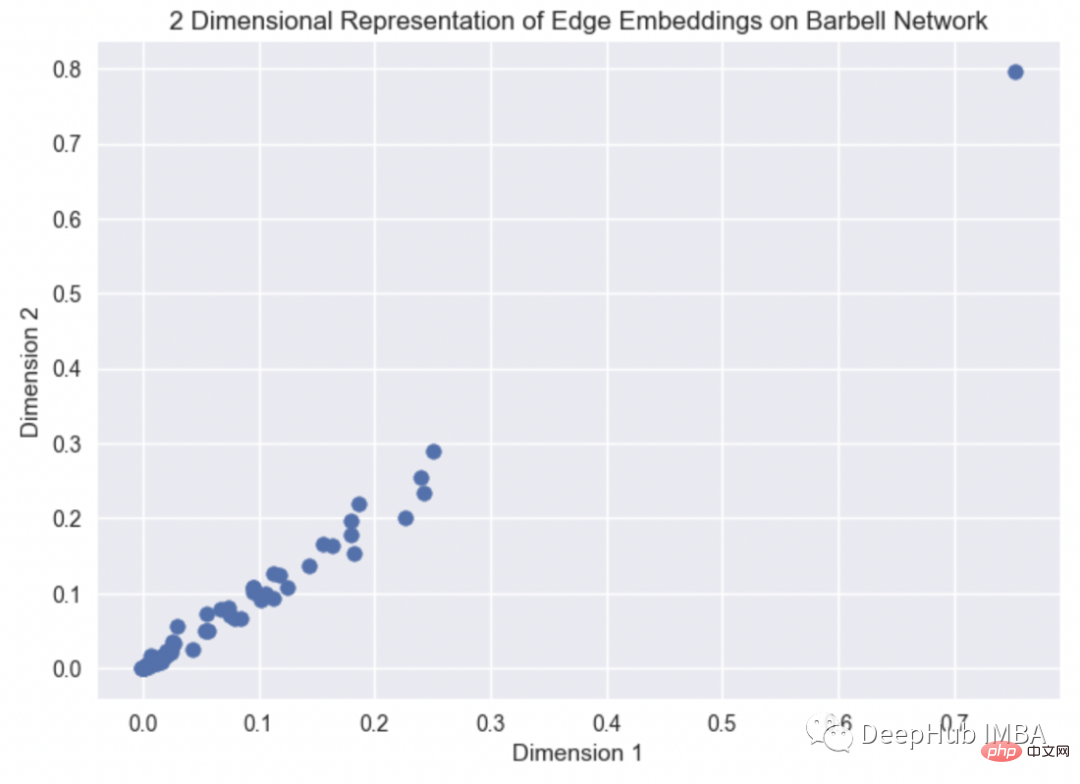
Voir la visualisation de l'intégration des bords via un graphique en haltères, le code source de Hammard Embedder peut être trouvé ici (https://github.com/eliorc/node2vec/blob/master/node2vec /edges.py#L91).

Incorporation de graphiques

n_graphs = 10
 Graphs = [
nx.fast_gnp_random_graph(
n = random.randint(5,15),
p = random.uniform(0,1)
) for x in range(n_graphs)
 ]
 
 g_mdl = Graph2Vec(dimensions=2)
 g_mdl.fit(Graphs)
 g_emb = g_mdl.get_embedding()
 
 x_coord = [vec[0] for vec in g_emb]
 y_coord = [vec[1] for vec in g_emb]
 
 plt.clf()
 plt.scatter(x_coord, y_coord)
 plt.xlabel("Dimension 1")
 plt.ylabel("Dimension 2")
 plt.title("2 Dimensional Representation of Graph Embeddings on Randomly Generated Networks")
 plt.show()

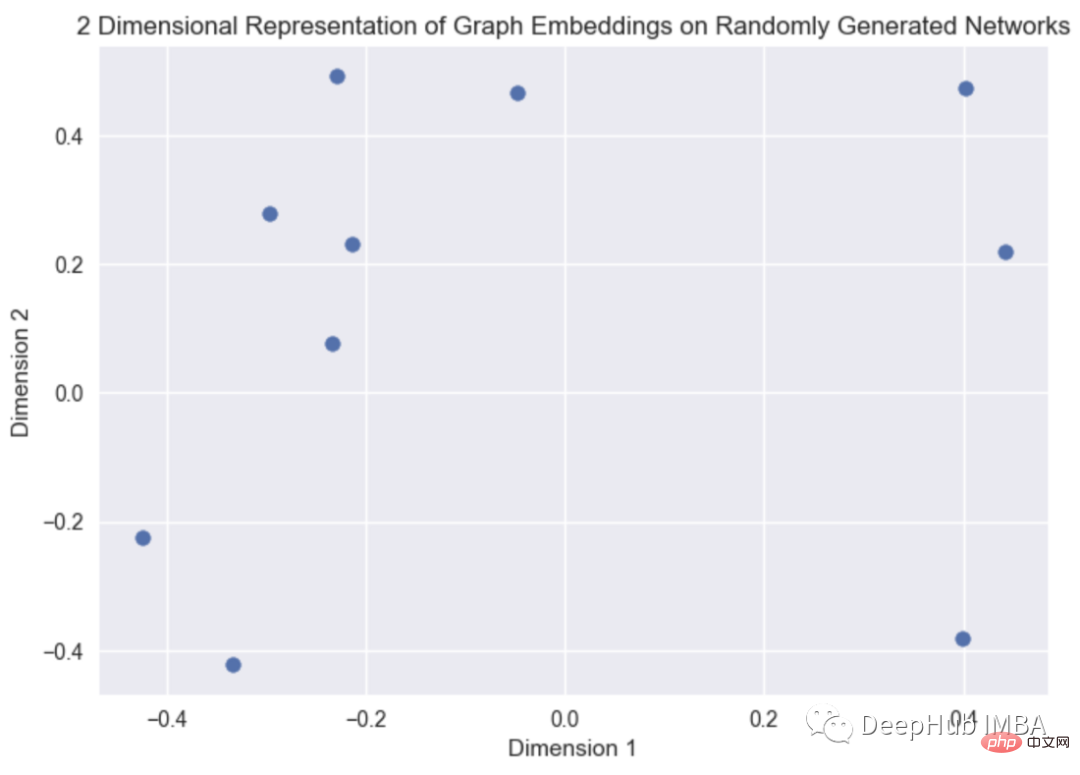
Il s'agit d'un graphe intégrant une visualisation de graphiques générés aléatoirement, le code source de l'algorithme graph2vec peut être trouvé ici. (https://karateclub.readthedocs.io/en/latest/_modules/karateclub/graph_embedding/graph2vec.html)

Résumé

Embedding est une fonction qui mappe des graphiques discrets à des représentations vectorielles. Diverses formes d'intégrations peuvent être générées à partir de données graphiques, d'intégrations de nœuds, d'intégrations d'arêtes et d'intégrations de graphiques. Les trois types d'intégrations fournissent une représentation vectorielle qui mappe la structure et les caractéristiques initiales du graphique aux valeurs numériques dans la dimension X.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!