Maison >Périphériques technologiques >IA >L'IA peut prouver 82 % des problèmes dans les bases de données mathématiques. Le nouveau SOTA a été réalisé et il est toujours basé sur Transformer.
L'IA peut prouver 82 % des problèmes dans les bases de données mathématiques. Le nouveau SOTA a été réalisé et il est toujours basé sur Transformer.
- 王林avant
- 2023-04-10 08:51:08886parcourir

Je dois dire que les scientifiques sont récemment obsédés par l'idée de donner des cours de mathématiques sur l'IA.
Non, l'équipe Facebook s'est également jointe à la fête et a proposé un nouveau modèle capable d'automatiser complètement la démonstration de théorèmes et qui est nettement meilleur que SOTA.
Vous devez savoir qu'à mesure que les théorèmes mathématiques deviennent plus complexes, il deviendra de plus en plus difficile de prouver les théorèmes uniquement par la puissance humaine.
Par conséquent, utiliser des ordinateurs pour démontrer des théorèmes mathématiques est devenu un axe de recherche.
OpenAI a également proposé précédemment un modèle GPT-f spécialisé dans cette direction, qui peut démontrer 56% des problèmes de Metamath.
La dernière méthode proposée cette fois peut augmenter ce nombre à 82,6%.
Dans le même temps, les chercheurs affirment que cette méthode prend moins de temps et peut réduire la consommation informatique à un dixième de celle d'origine par rapport au GPT-f.
Peut-on dire que cette fois l'IA réussira son combat contre les mathématiques ?
Ou Transformer
La méthode proposée dans cet article est un programme de formation en ligne basé sur Transformer.
peut être grossièrement divisé en trois étapes :
Première, pré-formation dans la bibliothèque de preuves mathématiques ;
Deuxièmement, affiner le modèle de politique sur l'ensemble de données supervisé ;
Troisième, en ligne ; Modèle de stratégie de formation et modèle de jugement.
Plus précisément, il utilise un algorithme de recherche pour permettre au modèle d'apprendre de la bibliothèque de preuves mathématiques existante, puis de le promouvoir pour prouver davantage de problèmes.
Il existe trois types de bibliothèques de preuves mathématiques, à savoir Metamath, Lean et un environnement de preuve auto-développé.
Pour faire simple, ces bibliothèques de preuves convertissent le langage mathématique ordinaire en une forme similaire à un langage de programmation.
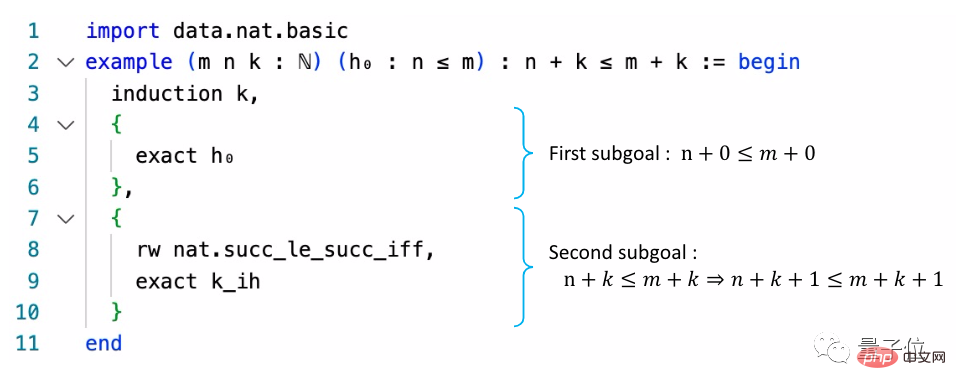
La bibliothèque principale de Metamath est set.mm, qui contient environ 38 000 preuves basées sur la théorie des ensembles ZFC.
Lean est mieux connu comme l'algorithme d'IA de Microsoft qui peut participer aux compétitions de l'OMI. La bibliothèque Lean est conçue pour enseigner à l'algorithme du même nom toutes les connaissances mathématiques du premier cycle et lui permettre d'apprendre à prouver ces théorèmes.
L'objectif principal de cette recherche est de construire un prouveur capable de générer automatiquement une série de stratégies appropriées pour prouver des problèmes.
À cette fin, les chercheurs ont proposé un algorithme de recherche de preuve d'hypergraphe hors équilibre basé sur MCTS.
MCTS est traduit par Monte Carlo Tree Search, qui est souvent utilisé pour résoudre les problèmes d'arbre de jeu. Il est bien connu grâce à AlphaGo.
Son processus de fonctionnement consiste à trouver des actions prometteuses en échantillonnant aléatoirement dans l'espace de recherche, puis à élargir l'arbre de recherche en fonction de cette action.
L'idée adoptée dans cette étude est similaire à celle-ci.
Le processus de preuve de recherche commence à partir de l'objectif g, recherche des méthodes vers le bas et se développe progressivement vers un hypergraphe.
Lorsqu'un ensemble vide apparaît sous une branche, cela signifie qu'une preuve optimale a été trouvée.
Enfin, pendant le processus de rétropropagation, enregistrez les valeurs des nœuds et le nombre total d'opérations du supertree.
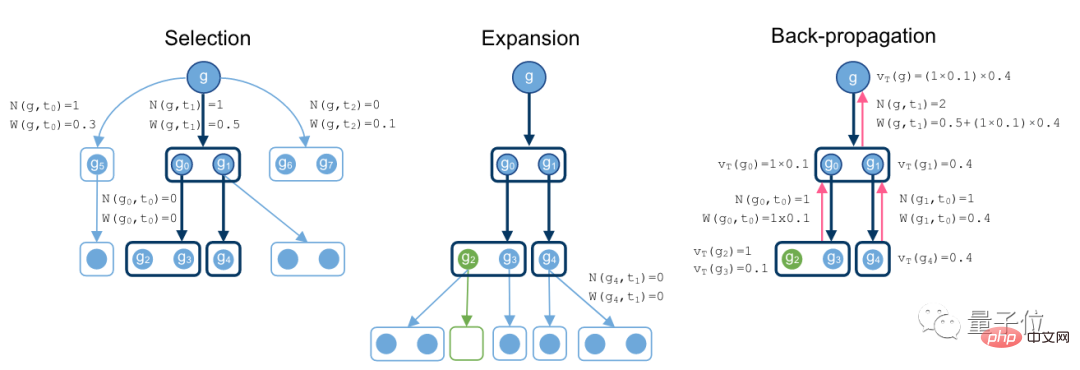
Dans ce lien, les chercheurs ont supposé un modèle de stratégie et un modèle de jugement.
Le modèle de politique permet un échantillonnage par le modèle de jugement, qui peut évaluer la capacité de la stratégie actuelle à trouver des méthodes de preuve.
L'ensemble de l'algorithme de recherche est basé sur les deux modèles ci-dessus comme référence.
Ces deux modèles sont des modèles Transformer et partagent des poids.
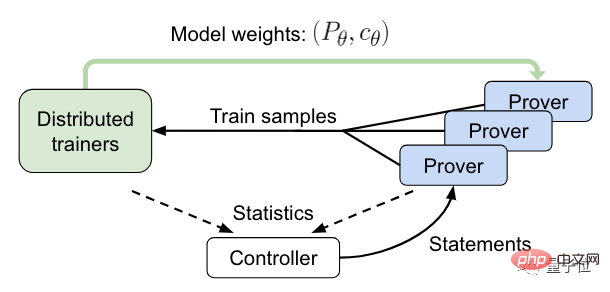
Vient ensuite l’étape de formation en ligne.
Dans ce processus, le contrôleur enverra la déclaration à une vérification HTPS asynchrone et collectera les données de formation et de preuve.
Le validateur enverra ensuite les échantillons de formation au formateur distribué et synchronisera périodiquement sa copie du modèle.
Résultats expérimentaux
Lors de la session de test, les chercheurs ont comparé HTPS avec GPT-f.
Ce dernier est un modèle de raisonnement par théorème mathématique précédemment proposé par OpenAI, également basé sur Transformer.
Les résultats montrent que le modèle après formation en ligne peut prouver 82% des problèmes dans Metamath, dépassant de loin le record précédent de 56,5% de GPT-f.

Dans la bibliothèque Lean, ce modèle peut prouver 43 % des théorèmes, soit 38 % de plus que SOTA. Voici les questions du test IMO prouvées par ce modèle.

Mais ce n’est pas encore parfait.
Par exemple, dans la question suivante, cela n'a pas résolu la question de la manière la plus simple. Les chercheurs ont dit que c'était parce qu'il y avait des erreurs dans les annotations.

One More Thing
Utilisation d'ordinateurs pour démontrer des problèmes mathématiques, la preuve du théorème des quatre couleurs est l'un des exemples les plus connus.
Le théorème des quatre couleurs est l'un des trois problèmes majeurs des mathématiques modernes. Il stipule que "n'importe quelle carte ne peut utiliser que quatre couleurs pour colorer les pays ayant des frontières communes dans des couleurs différentes".
Étant donné que la démonstration de ce théorème nécessite de nombreux calculs, personne n'a pu le démontrer pleinement dans les 100 ans suivant sa proposition.
Jusqu'en 1976, après 1 200 heures et 10 milliards de jugements sur deux ordinateurs de l'Université de l'Illinois, il était enfin possible de démontrer que n'importe quelle carte n'a besoin que de 4 couleurs pour la marquer, ce qui a également fait sensation dans toute la frontière mathématique.
De plus, à mesure que les problèmes mathématiques deviennent plus complexes, il devient plus difficile d'utiliser la puissance humaine pour vérifier si le théorème est correct.
Récemment, la communauté de l'IA s'est progressivement concentrée sur les problèmes mathématiques.
En 2020, OpenAI a lancé le modèle de raisonnement de théorème mathématique GPT-f, qui peut être utilisé pour la preuve automatique de théorèmes.
Cette méthode peut compléter 56,5 % des preuves de l'ensemble de tests, dépassant de plus de 30 % le modèle SOTA MetaGen-IL de l'époque.
La même année, Microsoft a également publié Lean, qui peut créer des questions de test IMO, ce qui signifie que l'IA peut poser des questions qu'elle n'a jamais vues auparavant.
L'année dernière, après qu'OpenAI ait ajouté un vérificateur à GPT-3, l'effet de la résolution de problèmes mathématiques était nettement meilleur que la méthode de réglage fin précédente, et il pouvait atteindre 90 % du niveau des élèves du primaire.
En janvier de cette année, une étude conjointe du MIT + Harvard + Columbia University + University of Waterloo a montré que le modèle qu'ils proposaient pouvait faire des mathématiques avancées.
En bref, les scientifiques travaillent dur pour faire de l'IA, un sujet partiel, capable à la fois d'arts et de sciences.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

