Maison >Périphériques technologiques >IA >Dernière recherche PNAS : taux de résolution de problèmes de 81 %, le réseau neuronal Codex ouvre la porte au monde des mathématiques avancées
Dernière recherche PNAS : taux de résolution de problèmes de 81 %, le réseau neuronal Codex ouvre la porte au monde des mathématiques avancées
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-09 15:51:061489parcourir
Récemment, une nouvelle étude a été publiée dans PNAS, qui a une fois de plus rafraîchi les capacités des réseaux de neurones. Cette fois, le réseau de neurones a été utilisé pour résoudre des problèmes de mathématiques avancés, et il s'agissait de problèmes de mathématiques difficiles dans le cours de mathématiques du MIT !
Dans cette nouvelle étude, l'équipe de recherche a prouvé que le modèle Codex d'OpenAI peut effectuer une synthèse de programme pour résoudre des problèmes mathématiques à grande échelle et résoudre automatiquement 81 % des problèmes de cours de mathématiques dans l'ensemble de données grâce à l'apprentissage de petits échantillons et au Codex. La performance dans ces tâches atteint le niveau humain. L'émergence de cette recherche bouleverse la croyance commune selon laquelle les réseaux de neurones ne peuvent pas résoudre le consensus sur les mathématiques avancées. sur la question. L'équipe de recherche a souligné que la raison pour laquelle le Codex peut atteindre de telles capacités est précisément parce que l'équipe a réalisé une innovation majeure. Ces études infructueuses dans le passé utilisaient uniquement une pré-formation basée sur des textes, et le réseau neuronal du Codex qui est apparu cette fois-ci ne l'a pas été. seule la pré-formation est effectuée sur la base du texte et le code est également affiné.
 L'ensemble de données sur les problèmes étudiés a été sélectionné parmi six cours de mathématiques du MIT et un cours de mathématiques de l'Université de Columbia. 25 problèmes ont été sélectionnés au hasard parmi sept cours : calcul à variable unique du MIT, calcul multivariable, équations de calcul différentiel, introduction aux probabilités et. Statistiques, algèbre linéaire et mathématiques pour l'informatique et COMS3251 Algèbre linéaire computationnelle de l'Université de Columbia.
L'ensemble de données sur les problèmes étudiés a été sélectionné parmi six cours de mathématiques du MIT et un cours de mathématiques de l'Université de Columbia. 25 problèmes ont été sélectionnés au hasard parmi sept cours : calcul à variable unique du MIT, calcul multivariable, équations de calcul différentiel, introduction aux probabilités et. Statistiques, algèbre linéaire et mathématiques pour l'informatique et COMS3251 Algèbre linéaire computationnelle de l'Université de Columbia.
Dans le même temps, l'équipe de recherche a utilisé MATH, un dernier benchmark de problèmes mathématiques avancés utilisé pour évaluer le raisonnement mathématique, pour tester la capacité d'OpenAI Codex. MATH couvre 6 sections mathématiques majeures : l'algèbre élémentaire, l'algèbre, le comptage et les probabilités. et niveau intermédiaire. Il y a 15 problèmes chacun d'algèbre, de théorie des nombres et de précalcul.
Légende : Ensemble de données de questions de cours et référence MATH utilisées dans l'étude
L'étude a montré que le Codex a résolu 213 des 265 questions de l'ensemble de données de questions et de l'ensemble de données MATH. Il est résolu automatiquement.
 1
1
Après la sortie de Transformer, les modèles de langage basés sur Transformer ont obtenu un grand succès dans diverses tâches de traitement du langage naturel (NLP), y compris les tâches linguistiques à tir zéro et à quelques tirs. Mais comme Transformer n’est pré-entraîné que sur le texte, ces modèles sont fondamentalement incapables de résoudre des problèmes mathématiques. GPT-3 en est un exemple typique.
Plus tard, grâce à un apprentissage en quelques étapes et à des invites de chaîne de pensée (CoT), les capacités de raisonnement mathématique de GPT-3 ont été améliorées, cependant, sans code, même avec un apprentissage en petites étapes et des astuces CoT, GPT-3 est ; toujours impuissant face aux problèmes de mathématiques de niveau collégial et au benchmark MATH.
Des recherches antérieures sur la résolution de problèmes mathématiques peuvent avoir abouti à certains résultats à un niveau mathématique relativement simple. Par exemple, les techniques qui valident ou prédisent des arbres d'expression basés sur des résultats de formation collaborative, telles que MAWPS et Math23k, peuvent résoudre des problèmes mathématiques au niveau de l'école primaire avec une précision de plus de 81 %, mais elles ne peuvent pas résoudre les problèmes mathématiques au niveau secondaire, aux Olympiades ou au niveau collégial. cours de mathématiques. La co-formation combinée aux réseaux de neurones graphiques (GNN) pour prédire les arbres d'expression arithmétique permet de résoudre des problèmes d'apprentissage automatique de niveau universitaire avec une précision allant jusqu'à 95 %. Mais ce travail s'est également limité à des réponses numériques, a produit un surapprentissage et n'a pas pu être généralisé à d'autres cours.
L'une des plus grandes innovations de ce travail est que non seulement le modèle Transformer tel que Codex a été pré-entraîné sur le texte, mais également affiné sur le code, afin qu'il puisse générer des solutions mathématiques à grande échelle. programme de problèmes.
L'équipe de recherche a sélectionné au hasard des échantillons de questions dans l'ensemble de données qui ne nécessitaient pas d'images d'entrée ou de preuves pour les tests. Parmi eux, un modèle de langage pré-entraîné uniquement sur le texte (GPT-3 text-davinci-002) n'a résolu automatiquement que 18 % des problèmes du cours et 25,5 % des problèmes du benchmark MATH.
En revanche, un programme synthétisé à l'aide d'un apprentissage zéro-shot et d'un réseau de neurones pré-entraîné sur le texte et affiné sur le code (OpenAI Codex code-davinci-002) peut résoudre automatiquement 71 % des problèmes du cours et 72,2 % des Questions de référence MATH.
En utilisant le même réseau neuronal Codex et un apprentissage en quelques étapes, il peut résoudre automatiquement 81 % des problèmes du cours et 81,1 % des problèmes du test de référence MATH. Cependant, 19 % des questions de cours et 18,9 % des questions de référence MATH que les modèles restants n'ont pas pu résoudre automatiquement ont finalement été résolues via des invites manuelles.
L'ajout de la méthode d'apprentissage sur petits échantillons est la deuxième innovation majeure de cette recherche. Comme le montre la figure ci-dessus, lorsque l'apprentissage par tir zéro ne peut pas répondre à la question, la paire (question, code) (paire) sera utilisée pour effectuer un apprentissage par petits coups :
1) Utilisation de la similarité de texte d'OpenAI- babbage-001 Le moteur d'intégration intègre toutes les questions ;
2) Calculez les questions résolues les plus similaires pour ouvrir les questions de leurs cours en utilisant la similarité cosinus intégrée
3) Combinez les questions les plus similaires avec leurs codes correspondants ; exemple d'un petit échantillon de problème.
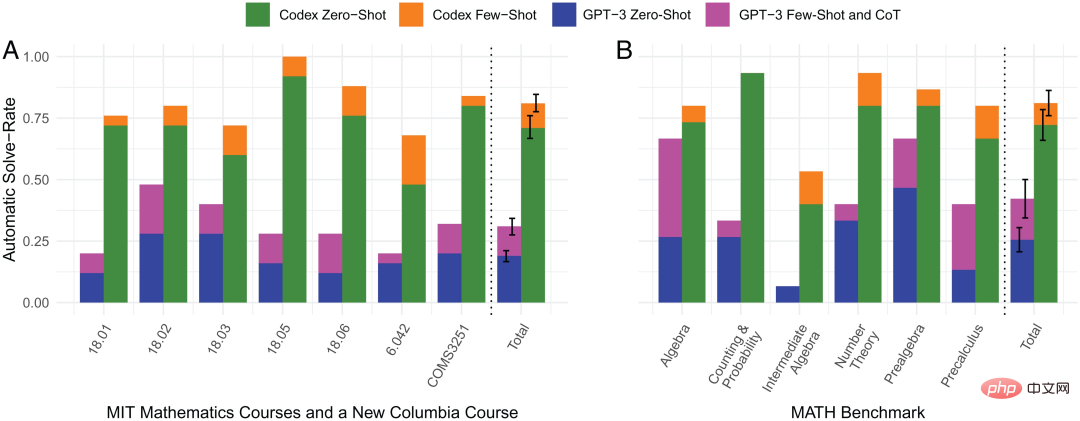
Note d'image : Comparaison des taux de résolution automatique de problèmes dans 4 méthodes
Les images ci-dessus sont l'apprentissage zéro-shot du Codex, l'apprentissage small-shot et l'apprentissage zéro-shot et small- apprentissage par tir. Comparaison des taux de résolution automatique de problèmes parmi 4 méthodes. On peut voir sur la figure que le petit échantillon d'apprentissage du Codex représenté par la barre orange a d'excellentes performances en termes de taux de résolution automatique de problèmes, et ses performances dans pratiquement tous les domaines mathématiques sont plus fortes que les trois autres méthodes.
La troisième innovation majeure de cette recherche est de fournir un pipeline pour résoudre des problèmes mathématiques et expliquer pourquoi la solution est telle. La figure suivante montre le flux d'exécution du pipeline dans les 5 cours de mathématiques du MIT.

En prenant comme exemple le problème de calcul à variable unique 18.01, étant donné un problème et le préfixe généré automatiquement "Utiliser SymPy", le Codex est invité et génère un programme. L'exécution du programme produit une équation avec la bonne réponse. Le programme demande ensuite automatiquement à nouveau le Codex, ce qui entraîne une explication du code générée.
2 Après la résolution de problèmes
En plus de résoudre des problèmes mathématiques et d'expliquer les réponses, le Codex est également utilisé pour générer de nouvelles questions pour chaque cours.
Afin d'évaluer le niveau des questions générées, l'équipe a mené une enquête auprès des étudiants du MIT ayant participé à ces cours ou cours du même niveau, principalement pour comparer la qualité et la difficulté des questions générées automatiquement et écrites manuellement. questions.
Dans chacun des 6 cours du MIT, 5 questions écrites à la main et 5 questions générées par modèle sont mélangées et présentées de manière aléatoire. Pour chacune des 60 questions, les étudiants participants ont été invités à répondre à 3 questions du sondage :
1) Pensez-vous que cette question a été écrite par un humain ou générée par une machine ?
2) Pensez-vous que cette question est appropriée ou inappropriée pour un cours spécifique ?
3 ) Sur une échelle de 1 (le plus facile) et 5 (le plus difficile), quel serait selon vous le niveau de difficulté de cette question ?
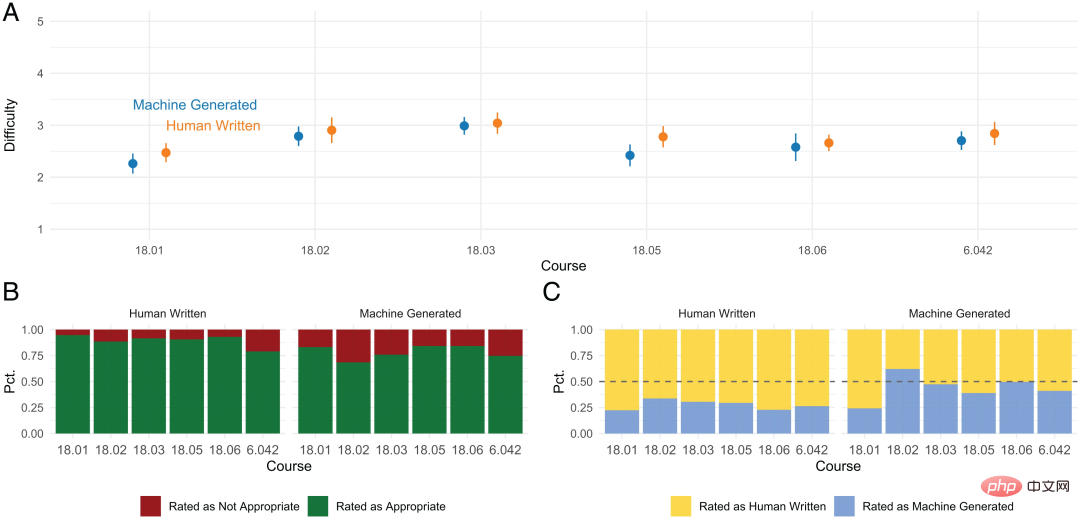
Dans les questionnaires retournés, les résultats de l'enquête auprès des étudiants sont résumés comme suit :
- La difficulté des questions générées par la machine et écrites par l'homme est similaire.
- Les questions écrites par des humains sont plus adaptées au cours que les questions générées automatiquement.
- Les réponses écrites par l'homme sont difficiles à identifier de manière incorrecte, tandis que les questions générées par la machine sont considérées par les étudiants comme étant soit générées par la machine, soit écrites par l'homme.
Les questions générées par la machine sont devenues indiscernables pour les étudiants, ce qui indique que le Codex a atteint les niveaux de performance humaine dans la génération de nouveau contenu.
Cependant, il existe également des problèmes que le modèle ne peut pas résoudre, tels que des problèmes auxquels il ne peut pas répondre s'ils apparaissent sous forme d'images ou d'autres formes non textuelles ; Par exemple, la décomposition de très grands nombres premiers ne peut pas être résolue par ce modèle. Cependant, ce dernier type de questions ne devrait apparaître dans aucun cours de mathématiques car même les vrais étudiants ne peuvent pas y répondre.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

