Qu’ont étudié les CVPR 2022 Best Student Paper Awards de Tongji et Alibaba ? Ceci est une interprétation d'une œuvre

Cet article explique notre travail "EPro-PnP : Perspective-n-Points probabilistes généralisés de bout en bout pour l'estimation de la pose d'objets monoculaires" qui a remporté le prix du meilleur article étudiant CVPR 2022. Le problème étudié dans cet article est d'estimer la pose d'un objet dans l'espace 3D à partir d'une seule image. Parmi les méthodes existantes, les méthodes d'estimation de pose basées sur l'optimisation géométrique PnP extraient souvent des points de corrélation 2D-3D à travers des réseaux profonds. Cependant, comme la solution optimale de pose n'est pas différentiable lors de la rétro-propagation, il est difficile d'utiliser l'erreur de pose car la perte s'effectue. un entraînement stable de bout en bout du réseau, lorsque les points de corrélation 2D-3D reposent sur la supervision des pertes d'autres agents, ce qui n'est pas un objectif d'entraînement optimal pour l'estimation de pose.

Afin de résoudre ce problème, nous nous sommes basés sur la théorie et avons proposé le module EPro-PnP, qui génère la distribution de densité de probabilité de la pose au lieu d'une seule solution optimale de la pose, remplaçant ainsi la pose optimale indifférenciable par différentiable. densité de probabilité, une formation stable de bout en bout est obtenue. EPro-PnP est très polyvalent et adapté à diverses tâches et données spécifiques. Il peut être utilisé pour améliorer les méthodes d'estimation de pose basées sur PnP existantes, ou il peut également utiliser sa flexibilité pour former de nouveaux réseaux. Dans un sens plus général, EPro-PnP introduit essentiellement la classification commune softmax dans le domaine continu et peut théoriquement être étendu pour former des modèles généraux avec des couches d'optimisation imbriquées.

Lien papier : https://arxiv.org/abs/2203.13254

Lien code : https://github.com/tjiiv-cprg/EPro-PnP

1. Introduction

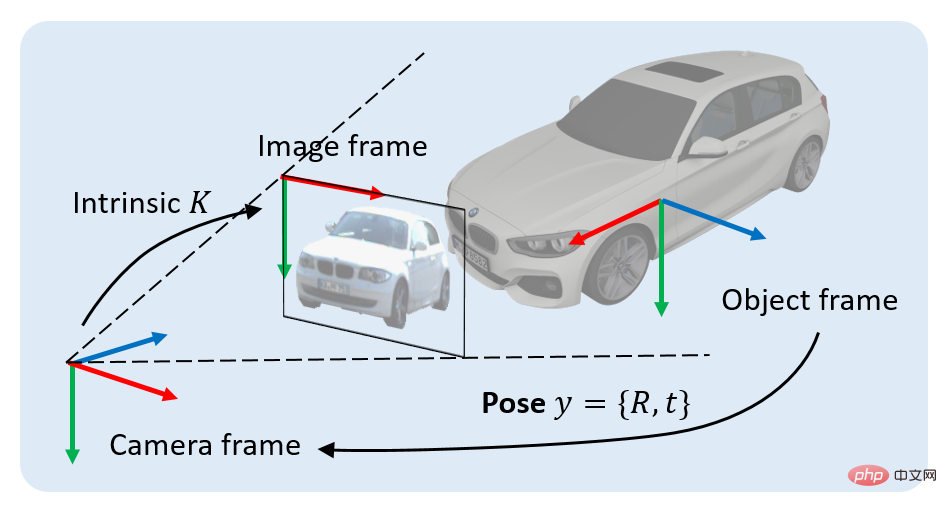
Nous étudions un problème classique en vision 3D : la localisation d'objets 3D à partir d'une seule image RVB. Plus précisément, étant donné une image contenant une projection d'un objet 3D, notre objectif est de déterminer la transformation d'un corps rigide du système de coordonnées de l'objet au système de coordonnées de la caméra. Cette transformation de corps rigide est appelée la pose de l'objet, notée y, qui contient deux parties : 1) la composante de position, qui peut être représentée par un vecteur de déplacement 3x1 t, 2) la composante d'orientation, qui peut être représentée par une rotation 3x3. la matrice R signifie.

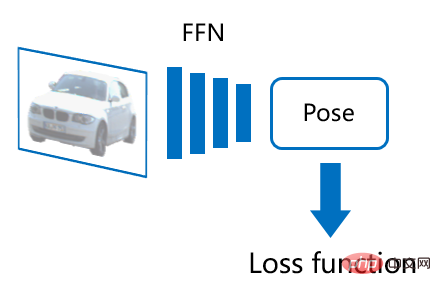
Pour résoudre ce problème, les méthodes existantes peuvent être divisées en deux catégories : explicites et implicites. La méthode explicite peut également être appelée prédiction directe de la pose, c'est-à-dire qu'elle utilise un réseau neuronal à action directe (FFN) pour générer directement chaque composant de la pose de l'objet, généralement : 1) prédire la profondeur de l'objet, 2) trouver le centre de l'objet La position de projection 2D du point sur l'image, 3) prédire l'orientation de l'objet (la méthode de traitement spécifique de l'orientation peut être plus compliquée). À l'aide de données d'image marquées avec la pose réelle de l'objet, une fonction de perte peut être conçue pour superviser directement les résultats de prédiction de pose, réalisant ainsi facilement une formation de bout en bout du réseau. Cependant, ces réseaux manquent d’interprétabilité et ont tendance à être surajustés sur des ensembles de données plus petits. Dans les tâches de détection d'objets 3D, les méthodes explicites dominent, en particulier pour les ensembles de données plus volumineux (tels que nuScenes).

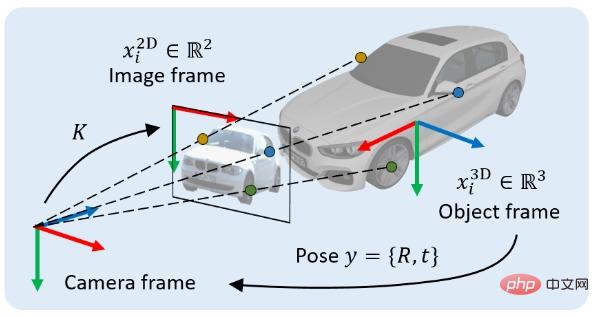
La méthode implicite est une méthode d'estimation de pose basée sur l'optimisation géométrique. Le représentant le plus typique est la Méthode d'estimation de pose basée sur PnP. Dans ce type de méthode, il faut d'abord trouver N points 2D dans le système de coordonnées de l'image (les coordonnées 2D du i-ième point sont notées ), et en même temps trouver les N points 3D qui leur sont associés dans le système de coordonnées de l'objet (le i-ème point). Les coordonnées 3D du point i sont marquées comme ), et parfois il est nécessaire d'obtenir le poids d'association de chaque paire de points (le poids d'association du i- la paire de points est marquée par ). Selon la contrainte de projection perspective, ces N paires de points associés pondérés 2D-3D définissent implicitement la pose optimale de l'objet. Plus précisément, on peut trouver la pose d'objet qui minimise l'erreur de reprojection :

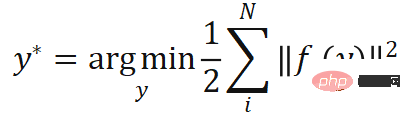
où 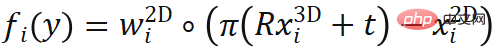, représente l'erreur de reprojection pondérée, qui est la fonction de la pose. représente la fonction de projection de la caméra contenant les paramètres internes, et 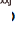représente l'élément produit. La méthode PnP est couramment utilisée dans les tâches d'estimation de pose 6-DOF où la géométrie de l'objet est connue.

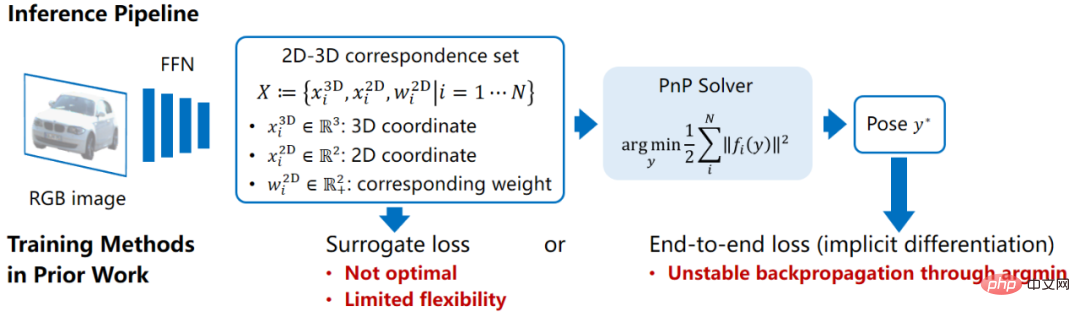
La méthode basée sur PnP nécessite également un réseau feedforward pour prédire l'ensemble de points associé 2D-3D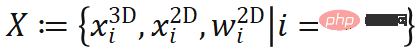. Comparé à la prédiction directe de pose, ce modèle d'apprentissage profond combiné aux algorithmes de vision géométrique traditionnels a une très bonne interprétabilité et ses performances de généralisation sont relativement stables. Cependant, il existe des défauts dans les méthodes de formation de modèles dans les travaux antérieurs. De nombreuses méthodes construisent une fonction de perte proxy pour superviser le résultat intermédiaire X, ce qui n'est pas un objectif optimal pour la pose. Par exemple, si la forme de l'objet est connue, les points clés 3D de l'objet peuvent être sélectionnés à l'avance, puis le réseau est entraîné pour trouver la position du point de projection 2D correspondante. Cela signifie également que la perte de substitution ne peut apprendre que certaines variables de X et n'est donc pas assez flexible. Que se passe-t-il si nous ne connaissons pas les formes des objets dans l’ensemble d’apprentissage et devons tout apprendre dans X à partir de zéro ?

Les avantages des méthodes explicites et implicites sont complémentaires. Si le réseau peut être entraîné de bout en bout pour apprendre l'ensemble de points associé X en supervisant les résultats de pose produits par PnP, les avantages des deux peuvent être combinés. Pour atteindre cet objectif, certaines études récentes ont mis en œuvre la rétropropagation des couches PnP en utilisant la dérivation de fonctions implicites. Cependant, la fonction argmin dans PnP est discontinue et non différenciable à certains points, ce qui rend la rétropropagation instable et la formation directe difficile à converger.

2. Introduction à la méthode EPro-PnP

1. Module EPro-PnP

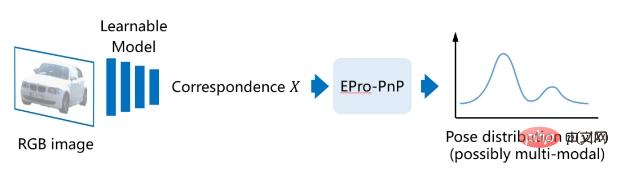
Afin d'obtenir une formation stable de bout en bout, nous avons proposé PnP probabiliste de bout en bout), à savoir EPro-PnP. L'idée de base est de considérer la pose implicite comme une distribution de probabilité, alors sa densité de probabilité est différentiable pour X. Premièrement, la fonction de vraisemblance de la pose est définie en fonction de l'erreur de reprojection :

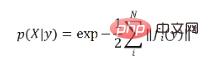
Si un a priori non informatif est utilisé, la densité de probabilité a posteriori de la pose est le résultat normalisé de la fonction de vraisemblance :

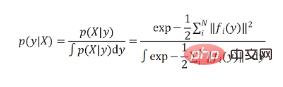
On peut remarquer que la formule ci-dessus est très proche de la formule de classification softmax couramment utilisée En fait, l'essence d'EPro-PnP est de déplacer le softmax d'un seuil discret à un seuil continu, et de le remplacer. la somme avec une intégrale .

2. Perte de divergence KL

Dans le processus d'entraînement du modèle, si la vraie pose de l'objet est connue , alors la distribution de pose cible peut être définie. À l'heure actuelle, la divergence KL 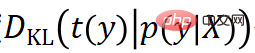peut être calculée comme la fonction de perte utilisée pour entraîner le réseau (parce que est fixe, elle peut également être comprise comme la fonction de perte d'entropie croisée). Lorsque la cible s'approche de la fonction Dirac, la fonction de perte basée sur la divergence KL peut être simplifiée sous la forme suivante :

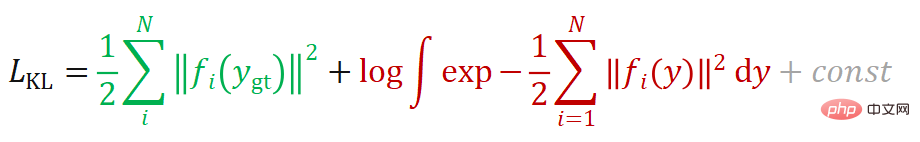
Si sa dérivée est dérivée :

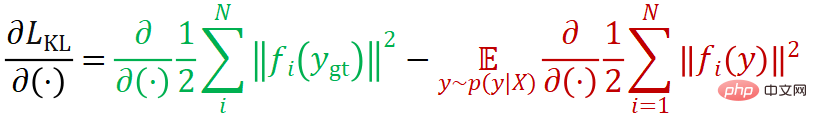
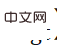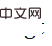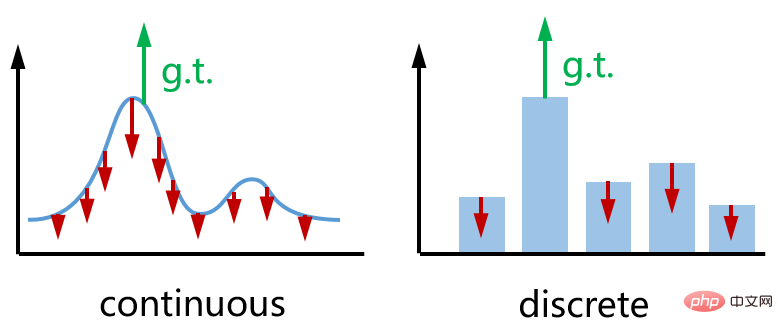
On peut voir que la fonction de perte se compose de deux éléments. Le premier terme (noté ) tente de réduire l'erreur de reprojection de la vraie valeur de la pose , et le deuxième terme (noté ). ) tente d'augmenter la prédiction Erreurs de reprojection partout dans la pose . Les deux directions sont opposées et l’effet est illustré dans la figure ci-dessous (à gauche). Par analogie, le côté droit est la perte d'entropie croisée catégorique que nous utilisons couramment lors de la formation des réseaux de classification.

3. Perte de Monte Carlo

Il convient de noter que le deuxième terme de la perte KL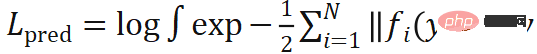 contient une intégrale. Cette intégrale n'a pas de solution analytique, elle doit donc être approximée par des méthodes numériques. Compte tenu de la polyvalence, de la précision et de l’efficacité des calculs, nous utilisons la méthode de Monte Carlo pour simuler la distribution des poses par échantillonnage.

Plus précisément, nous utilisons un algorithme d'échantillonnage par importance - Adaptive Multiple Importance Sampling (AMIS) pour calculer des échantillons de pose K 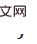avec des poids 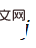, nous allons Ce processus s'appelle Monte Carlo PnP :

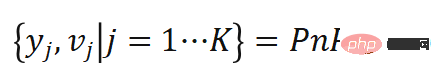
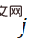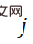Selon cela, le deuxième terme peut être approximé en fonction du poids , et peut être rétropropagé :

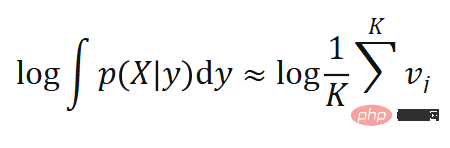
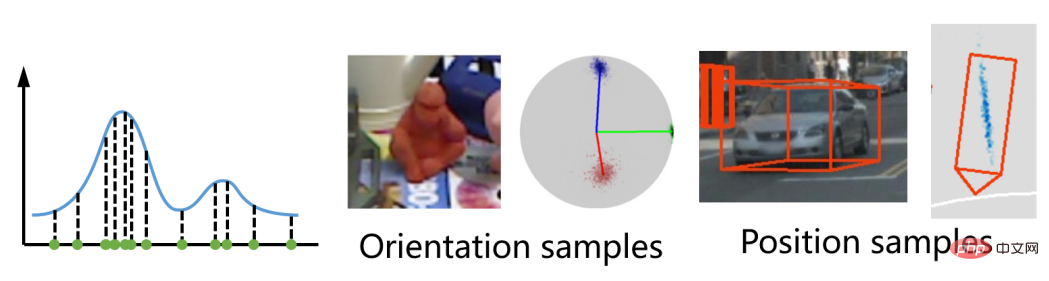
L'effet de visualisation de l'échantillonnage de pose est le suivant ci-dessous :

4. Régularisation dérivée pour le solveur PnP

Bien que la perte PnP de Monte Carlo puisse être utilisée pour entraîner le réseau afin d'obtenir une distribution de pose de haute qualité, dans la phase d'inférence, il est toujours nécessaire d'obtenir la position optimale via le solveur d'optimisation PnP Posture. solution. L'algorithme de Gauss-Newton couramment utilisé et ses dérivées résolvent grâce à une optimisation itérative, et son incrément itératif est déterminé par les dérivées première et seconde de la fonction de coût . Afin de rendre la solution de PnP plus proche de la vraie valeur , la dérivée de la fonction de coût peut être régularisée. La fonction de perte de régularisation est conçue comme suit :

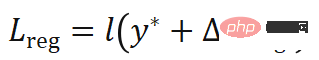
où, est l'incrément d'itération de Gauss-Newton, qui est lié aux dérivées du premier et du second ordre de la fonction de coût et peut être rétropropagé , représente la métrique de distance, utilisez L1 lisse pour la position et la similarité cosinus pour l'orientation. Lorsque est incohérent, cette fonction de perte force l'incrément d'itération à pointer vers la vraie valeur réelle.

3. Réseau d'estimation de pose basé sur EPro-PnP

Nous utilisons différents réseaux pour les deux sous-tâches d'estimation de pose à 6 degrés de liberté et de détection de cible 3D. Parmi eux, pour l'estimation de pose à 6 degrés de liberté, il est légèrement modifié sur la base du réseau CDPN de l'ICCV 2019 et formé avec EPro-PnP pour mener des études d'ablation pour la détection de cibles 3D, un tout nouveau réseau est conçu sur la base ; sur FCOS3D de l'ICCVW 2021 Tête de détection de correspondance déformable pour prouver qu'EPro-PnP peut entraîner le réseau à apprendre directement tous les points 2D-3D et poids d'association sans connaissance de la forme de l'objet, démontrant ainsi la flexibilité d'EPro-PnP dans les applications.

1. Réseau de corrélation dense pour l'estimation de pose 6-DOF

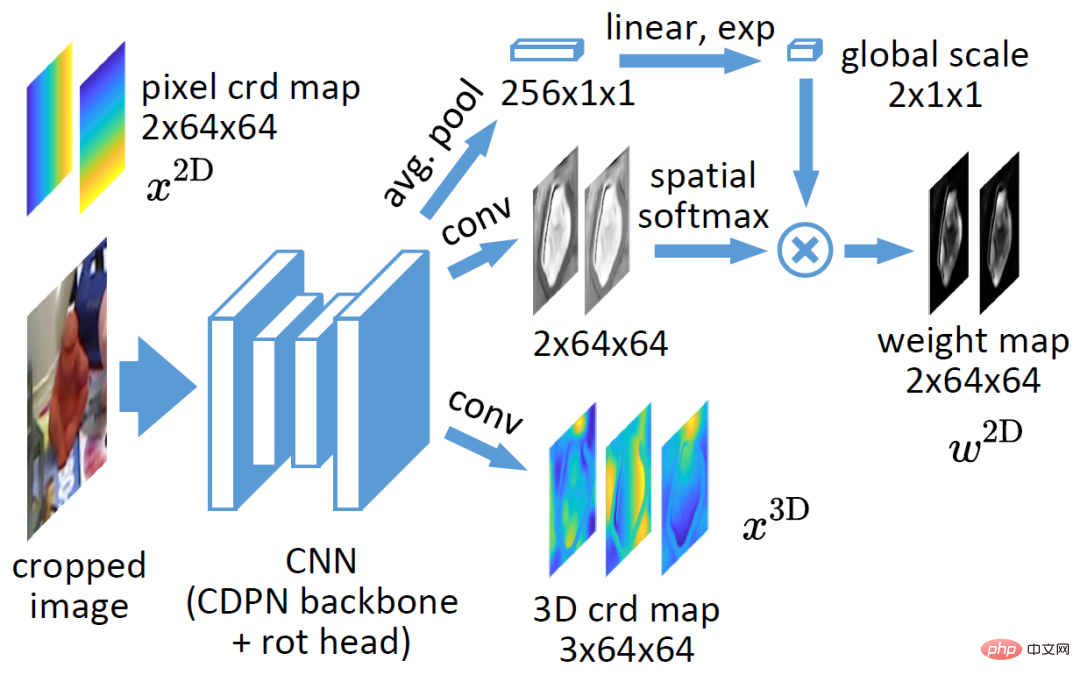
La structure du réseau est celle indiquée dans la figure ci-dessus, sauf que la couche de sortie est modifiée en fonction du CDPN d'origine. Le CDPN d'origine utilise la boîte 2D de l'objet détecté pour recadrer l'image régionale et l'entre dans le réseau fédérateur ResNet34. Le CDPN original découple la position et l'orientation en deux branches. La branche de position utilise la méthode explicite de prédiction directe, tandis que la branche d'orientation utilise la méthode implicite d'association dense et PnP. Afin d'étudier EPro-PnP, le réseau modifié conserve uniquement la branche de corrélation dense, dont la sortie est une carte de coordonnées 3D à 3 canaux, et un poids de corrélation à 2 canaux, où le poids de corrélation a subi un softmax spatial et une mise à l'échelle du poids global. Le but de l'ajout de softmax spatial est de normaliser le poids afin qu'il ait des propriétés similaires à la carte d'attention et puisse se concentrer sur des domaines relativement importants. Des expériences ont prouvé que la normalisation du poids est également la clé d'une convergence stable. La mise à l'échelle globale du poids reflète la concentration de la distribution des poses . Le réseau peut être entraîné avec uniquement la perte de pose Monte Carlo d'EPro-PnP, en plus de l'ajout d'une régularisation dérivée et d'une perte de régression de coordonnées 3D supplémentaire lorsque la forme de l'objet est connue.

2. Réseau de corrélation de déformation pour la détection de cibles 3D

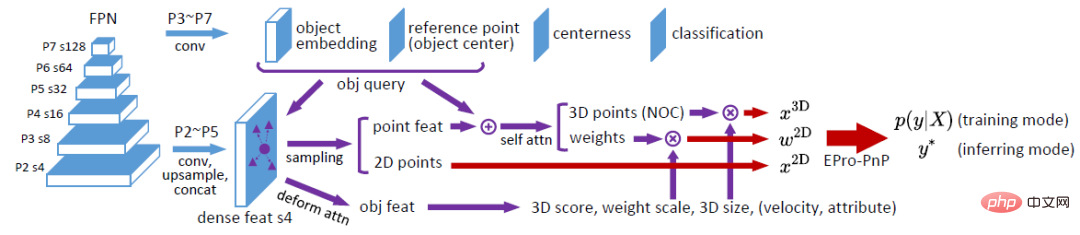
La structure du réseau est illustrée dans la figure ci-dessus. D'une manière générale, il est basé sur le détecteur FCOS3D et fait référence à la structure de réseau conçue par DETR déformable. Sur la base de FCOS3D, ses couches de centrage et de classification sont conservées, et sa couche de prédiction de pose d'origine est remplacée par des couches d'incorporation d'objets et de points de référence pour générer une requête d'objet. En se référant au DETR déformable, on obtient la position d'échantillonnage 2D en prédisant le décalage par rapport au point de référence (on obtient donc ). Les caractéristiques échantillonnées sont regroupées en caractéristiques d'objet via des opérations d'attention, qui sont utilisées pour prédire les résultats au niveau de l'objet (score 3D, échelle de poids, taille de la boîte 3D, etc.). De plus, après échantillonnage, les caractéristiques de chaque point sont ajoutées avec l'incorporation d'objets et traitées par auto-attention pour générer les coordonnées 3D et les poids associés 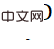correspondant à chaque point. Tous les prédits peuvent être entraînés par la perte de pose de Monte Carlo d'EPro-PnP, qui peut converger et atteindre une grande précision sans régularisation supplémentaire. Sur cette base, une perte de régularisation dérivée et une perte auxiliaire peuvent être ajoutées pour améliorer encore la précision.

IV.Résultats expérimentaux

1. Tâche d'estimation de pose à 6 degrés de liberté

Utilisez l'expérience de l'ensemble de données LineMOD et comparez-la strictement avec la ligne de base du CDPN. On peut voir qu'en ajoutant la perte EPro-PnP pour la formation de bout en bout, la précision est considérablement améliorée (+12,70). Continuez à augmenter la perte de régularisation dérivée et la précision est encore améliorée. Sur cette base, l'utilisation des résultats de formation du CDPN d'origine pour initialiser et augmenter les époques (en gardant le nombre total d'époques cohérent avec la formation complète en trois étapes du CDPN d'origine) peut encore améliorer la précision. la formation CDPN est issue de la formation complémentaire de supervision des masques CDPN.

L'image ci-dessus est une comparaison d'EPro-PnP avec diverses méthodes de pointe. EPro-PnP, qui est amélioré par rapport au CDPN arrière, est proche de SOTA en termes de précision, et l'architecture d'EPro-PnP est simple. Elle est entièrement basée sur PnP pour l'estimation de la pose et ne nécessite pas d'estimation de profondeur explicite supplémentaire ni d'affinement de la pose. Par conséquent, il existe également des avantages en termes d'efficacité.

2. Tâche de détection de cible 3D

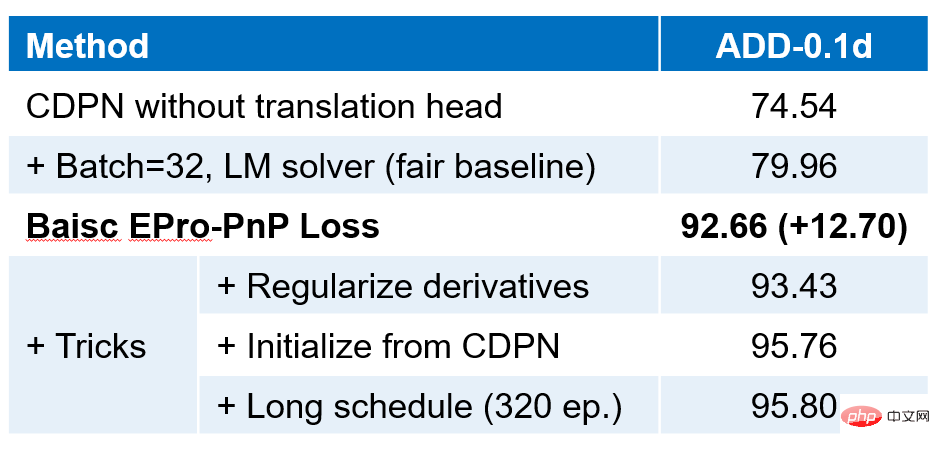
À l'aide de l'expérience de l'ensemble de données nuScenes, les résultats comparés à d'autres méthodes sont présentés dans la figure ci-dessus. EPro-PnP présente non seulement une amélioration significative par rapport à FCOS3D, mais surpasse également PGD, une autre version améliorée de SOTA et FCOS3D à l'époque. Plus important encore, EPro-PnP est actuellement le seul à utiliser des méthodes d'optimisation géométrique pour estimer la pose sur l'ensemble de données nuScenes. En raison de la grande échelle de l'ensemble de données nuScenes, le réseau d'estimation de pose directe entraîné de bout en bout présente déjà de bonnes performances, et nos résultats illustrent que l'entraînement de bout en bout d'un modèle basé sur l'optimisation géométrique peut obtenir de meilleures performances sur grands ensembles de données. Excellentes performances.

3. Analyse visuelle

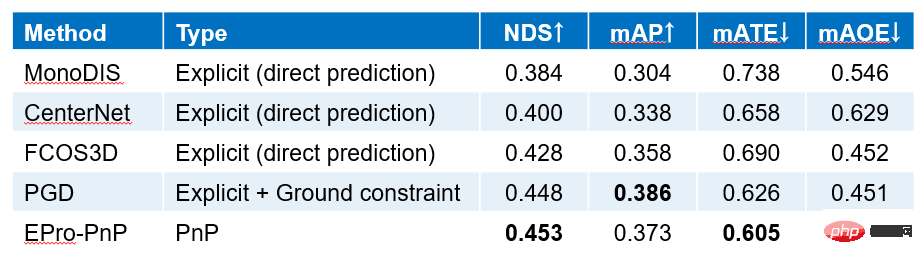
La figure ci-dessus montre les résultats de prédiction du réseau d'associations dense formé avec EPro-PnP. Parmi eux, le poids de corrélation map met en évidence des zones importantes de l'image, similaires au mécanisme d'attention. L'analyse de la fonction de perte montre que la zone de surbrillance correspond à la zone avec une faible incertitude de reprojection et qui est plus sensible aux changements de pose.

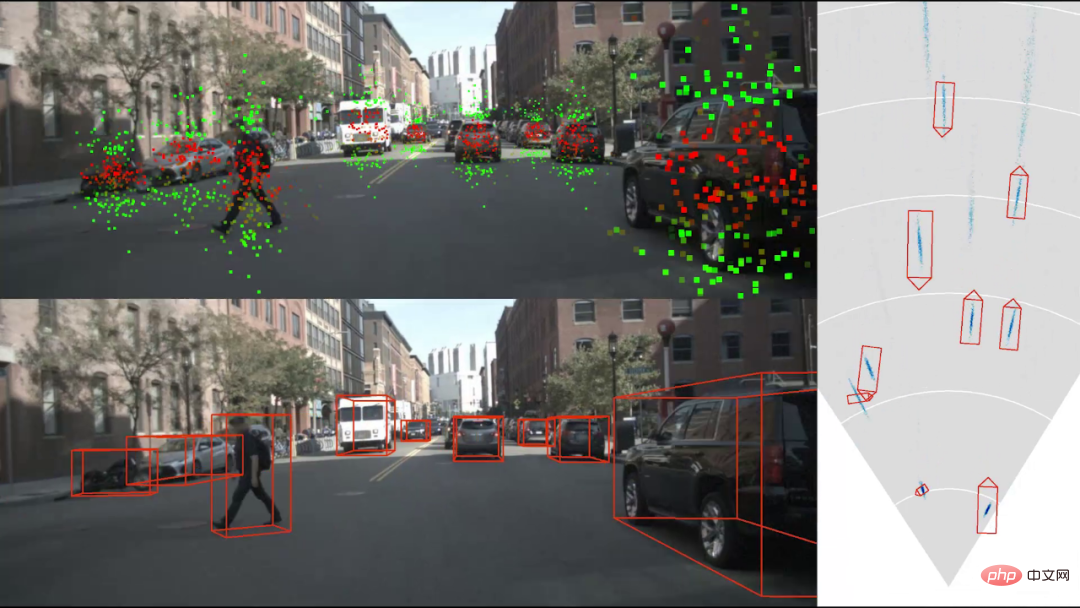
Les résultats de la détection de cible 3D sont présentés dans la figure ci-dessus. La vue supérieure gauche montre les positions des points 2D échantillonnés par le réseau de corrélation de déformation. Le rouge indique les points avec une composante X horizontale plus élevée et le vert indique les points avec une composante Y verticale plus élevée. Les points verts sont généralement situés aux extrémités supérieure et inférieure de l'objet. Leur fonction principale est de calculer la distance de l'objet en fonction de la hauteur de l'objet. Cette fonctionnalité n'est pas artificiellement spécifiée et est entièrement le résultat d'un entraînement gratuit. L'image de droite montre les résultats de la détection dans une vue de dessus, dans laquelle l'image du nuage bleu représente la densité de distribution du point central de l'objet, reflétant l'incertitude du positionnement de l'objet. Généralement, l’incertitude de positionnement des objets distants est supérieure à celle des objets proches. 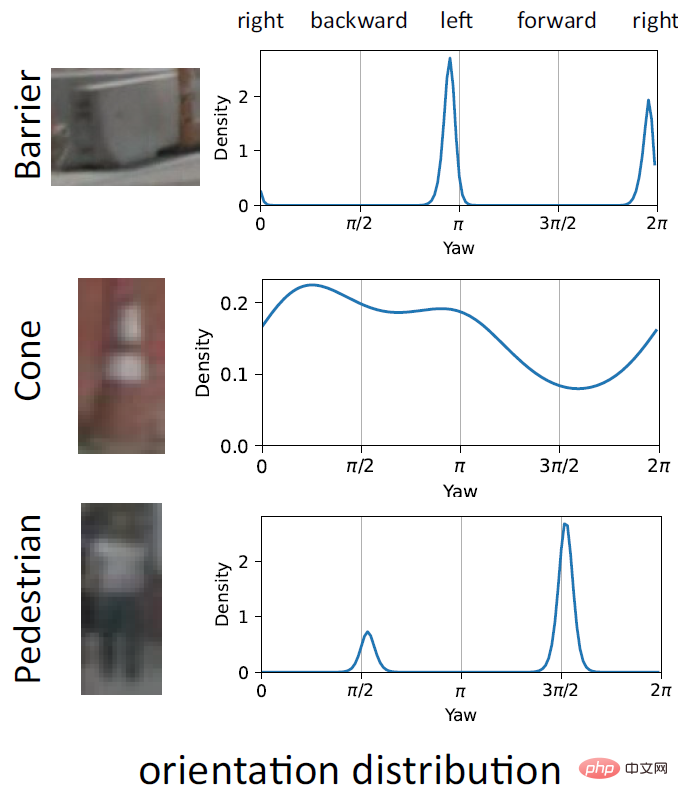Un autre avantage important d'EPro-PnP est la capacité de représenter les ambiguïtés d'orientation en prédisant des distributions multimodales complexes. Comme le montre la figure ci-dessus, la barrière a souvent deux pics avec une différence de 180° en raison de la symétrie de rotation de l'objet lui-même ; le cône lui-même n'a pas d'orientation spécifique, donc les résultats de la prédiction sont distribués dans toutes les directions ; symétrique, mais à cause de l'image, ce n'est pas clair, c'est difficile de distinguer l'avant et l'arrière, et parfois il y a deux pics. Cette caractéristique probabiliste fait qu'EPro-PnP ne nécessite aucun traitement spécial sur la fonction de perte pour les objets symétriques.

5. Résumé

EPro-PnP transforme la pose optimale indifférenciable d'origine en une densité de probabilité de pose différentiable, de sorte que le réseau d'estimation de pose basé sur l'optimisation géométrique PnP puisse obtenir un train de bout en bout stable et flexible. EPro-PnP peut être appliqué aux problèmes généraux d'estimation de la pose d'objets 3D Même lorsque la géométrie de l'objet 3D est inconnue, les points associés 2D-3D de l'objet peuvent être appris grâce à une formation de bout en bout. Par conséquent, EPro-PnP élargit les possibilités de conception de réseaux, comme notre réseau de corrélation de déformation proposé, qui était auparavant impossible à former.

De plus, EPro-PnP peut également être directement utilisé pour améliorer les méthodes d'estimation de pose basées sur PnP existantes, libérant ainsi le potentiel des réseaux existants grâce à une formation de bout en bout et améliorant la précision de l'estimation de pose. Dans un sens plus général, EPro-PnP introduit essentiellement la classification commune softmax dans le domaine continu. Elle peut non seulement être utilisée pour d'autres problèmes de vision 3D basés sur l'optimisation géométrique, mais peut également être théoriquement étendue pour former un modèle d'optimisation général imbriqué. .

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!