Maison >Périphériques technologiques >IA >Application de positionnement décisionnel basée sur un algorithme de forêt causale
Application de positionnement décisionnel basée sur un algorithme de forêt causale
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2023-04-08 11:21:102102parcourir
Traducteur | Zhu Xianzhong
Critique | Sun Shujuan
Dans mon précédentblog, nous avons expliquécomment utiliser cause et arbre à effets pour évaluer les effets hétérogènes du traitement de la politique. Si vous ne l'avez pas encore lulu, je vous suggère de le lire avant de lire cet article, car nous dans cet articlepensonsque vous comprenez déjà les de Quelques contenus liés à cet article.
Pourquoi les effets de traitement hétérogènes (HTE : effets de traitement hétérogènes) ? Premièrement, l'estimation des effets hétérogènes des traitements permet de choisir les traitements (médicaments, publicités, produits, etc.) utilisateurs (patients, utilisateurs, clients, etc.). En d'autres termes, on estime que HTE nous aide pour le ciblage. En fait, comme nous le verrons plus loin dans l'article, une approche de traitement , tout en apportant des avantages positifs à un sous-ensemble d'utilisateurs, peut être inefficace, voire contre-productive en moyenne. L'inverse pourrait aussi être vrai : un médicament est efficace en moyenne, mais l'est si on clarifie les informations sur les utilisateurs il a des effets secondaires , L'efficacité de ce médicament sera encore améliorée. Dans cet article, nous explorerons une extension de l'arbre causal - la forêt
causale. Tout comme les forêts aléatoires élargissent les arbres de régression en faisant la moyenne de plusieursarbres bootstrap ensemble, les forêts causales élargissent également les arbres causals. La principale différence vient du point de vue du raisonnement, qui est moins simple. Nous verrons également comment les résultats de différents algorithmes d’estimation HTE peuvent être comparés et comment ils peuvent être utilisés pour atteindre des objectifs politiques. Cas de réduction en lignePour le reste de cet article, nous continuons à utiliser
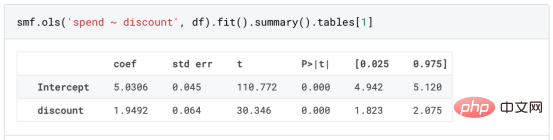
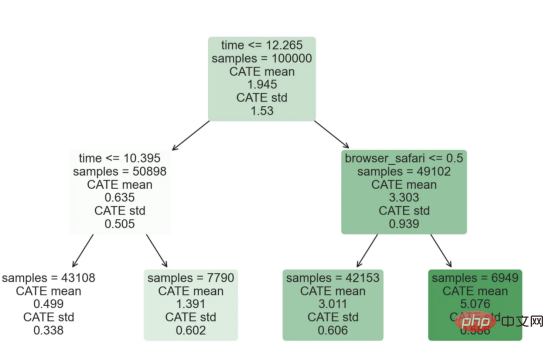
l'exemple de jouet utilisé dans mon dernier article sur les Arbres de causes et d'effets : supposons que nous soyons une boutique en ligne et nous avons Intéressé de savoir si offrir des réductions aux nouveaux clients augmente leurs dépenses en magasin.Pour voir si la réduction est une bonne affaire, nous avons mené l'expérience randomisée ou le test A/B suivant : chaque fois qu'un nouveau client parcourt notre boutique en ligne, nous lui attribuons au hasard une condition de traitement . Nous offrons des réductions aux utilisateurs soumis au traitement ; nous n'offrons pas de réductions aux utilisateurs contrôlés. J'importe le processus de génération de données dgp_online_discounts() à partir du fichier src.dgp. J'importe également certaines fonctions de dessin et bibliothèques depuis src.utilslibrary. Pour inclure non seulement du code, mais aussi des données et des tableaux et d'autres contenus , j'ai utilisé le framework Deepnote , un environnement de bloc-notes collaboratif de type Jupyter basé sur Web. Nous disposons de données sur 100 000 visiteurs de la boutique en ligne et nous observons l'heure à laquelle ils visitent le site Web, l'appareil qu'ils utilisent, le navigateur qu'ils utilisent et leur région géographique. Nous regardons également s'ils ont bénéficié d'une réduction, comment nous l'avons géré , combien ils ont dépensé, et quelques autres résultats intéressants. Étant donné que l'expérience est attribuée au hasard, nous pouvons utiliser une simple estimation de la différence moyenne pour estimer l'effet de l'expérience. Nous nous attendons à ce que le groupe expérimentalet le groupe témoin soient similaires, à l'exception de la remise, nous pouvons donc attribuer toute différence de dépenses à la remise. La réduction semble et elle semble fonctionner : les dépenses moyennes du groupe experiment ont augmenté de 1,95 $. Mais tous les clients sont-ils concernés de la même manière ? Pour répondre à cette question, nous souhaitons estimer les effets hétérogènes du traitement , éventuellement au niveau individuel. Il existe de nombreuses options différentes pour calculer les effets de traitement hétérogènes. L’approche la plus simple consiste à interagir avec le résultat qui nous intéresse en termes de dimensions d’hétérogénéité. Le problème avec cette approche est de savoir quelle variable choisir. Parfois, nous disposons d'informations qui peuvent guider nos actions à l'avance ; par exemple, nous pouvons savoir que les utilisateurs mobiles dépensent en moyenne plus que les utilisateurs d'ordinateurs de bureau. D’autres fois, nous pouvons être intéressés par une certaine dimension pour des raisons commerciales ; par exemple, nous pouvons vouloir investir davantage dans une certaine région. Cependant, lorsque nous ne disposons d’aucune information supplémentaire, nous souhaitons que le processus soit basé sur les données. effets hétérogènes du traitement - les arbres causals. Nous allons maintenant les étendre aux forêts causales. Cependant, avant de commencer, nous devons présenter son cousin non causal, la forêt aléatoire. La forêt aléatoire, comme son nom l'indique, est une extension de l'arbre de régression, en y ajoutant deux sources indépendantes d'aléatoire. En particulier, l'algorithme de forêt aléatoire est capable de faire des prédictions sur de nombreux arbres de régression différents, chacun formé sur des échantillons bootstrap des données, et d'en faire la moyenne ensemble. Ce processus est souvent appelé algorithme d'agrégation guidée, également connu sous le nom d'algorithme d'ensachage, et peut être appliqué à n'importe quel algorithme de prédiction et n'est pas spécifique aux forêts aléatoires. Une source supplémentaire de caractère aléatoire provient de la sélection des caractéristiques, puisqu'à chaque division, seul un sous-ensemble aléatoire de toutes les caractéristiques X est pris en compte pour la répartition optimale. Ces deux sources supplémentaires d'aléatoire sont très importantes et contribuent à améliorer les performances des forêts aléatoires. Premièrement, l’algorithme de bagging permet aux forêts aléatoires de produire des prédictions plus fluides que les arbres de régression en faisant la moyenne de plusieurs prédictions discrètes. En revanche, la sélection aléatoire de fonctionnalités permet aux forêts aléatoires d’explorer l’espace des fonctionnalités plus en profondeur, leur permettant ainsi de découvrir plus d’interactions que de simples arbres de régression. En fait, il peut y avoir des interactions entre des variables qui ne sont pas très prédictives en elles-mêmes (et donc peu conflictuelles), mais qui sont très puissantes ensemble. Les forêts causales sont équivalentes aux forêts aléatoires, mais sont utilisées pour estimer les effets hétérogènes du traitement, exactement comme les arbres causals et les arbres de régression. Comme pour les arbres causals, nous avons un problème fondamental : nous souhaitons prédire un objet que nous n'avons pas observé : l'effet individuel du traitement τᵢ. La solution est de créer une variable de résultat auxiliaire Y* dont la valeur attendue pour chaque observation est exactement l'effet du traitement . Variable de résultat auxiliaire Si vous souhaitez en savoir plus sur pourquoi cette variable n'a aucun effet sur le traitement individuel ajoute du biais Si vous souhaitez le définir , veuillez jeter un œil mon article précédent , j'ai présenté en détail dans cet article. En bref, vous pouvez penser à Une fois que nous avons une variable de résultat, nous devons faire quelques choses supplémentaires afin d'utiliser des forêts aléatoires pour estimer les effets de traitement hétérogènes. Tout d’abord, nous devons construire l’arbre avec le même nombre d’unités de traitement et d’unités de contrôle sur chaque feuille. Deuxièmement, nous devons utiliser différents échantillons pour construire l’arbre et l’évaluer, c’est-à-dire calculer le résultat moyen pour chaque feuille. Ce processus est souvent appelé arbres honnêtes car nous pouvons traiter les échantillons de chaque feuille comme étant indépendants de la structure de l'arbre, ce qui le rend très utile pour l'inférence. Avant de procéder à l'évaluation, générons des variables factices pour les variables catégorielles appareil, navigateur et région. 与因果树不同,因果森林更难解释,因为我们无法可视化每一棵树。我们可以使用SingleTreeateInterpreter函数来绘制因果森林算法的等效表示。 因果森林模型表示 我们可以像因果树模型一样解释树形图。在顶部,我们可以看到数据中的平均$Y^*$的值为1.917$。从那里开始,根据每个节点顶部突出显示的规则,数据被拆分为不同的分支。例如,根据时间是否晚于11.295,第一节点将数据分成大小为46878$和53122$的两组。在底部,我们得到了带有预测值的最终分区。例如,最左边的叶子包含40191$的观察值(时间早于11.295,在非Safari浏览器环境下),我们预测其花费为0.264$。较深的节点颜色表示预测值较高。 这种表示的问题在于,与因果树的情况不同,它只是对模型的解释。由于因果森林是由许多自助树组成的,因此无法直接检查每个决策树。了解在确定树分割时哪个特征最重要的一种方法是所谓的特征重要性。 显然,时间是异质性的第一个维度,其次是设备(特别是移动设备)和浏览器(特别是Safari)。其他维度无关紧要。 现在,让我们检查一下模型性能如何。 通常,我们无法直接评估模型性能,因为与标准的机器学习设置不同,我们没有观察到实际情况。因此,我们不能使用测试集来计算模型精度的度量。然而,在我们的案例中,我们控制了数据生成过程,因此我们可以获得基本的真相。让我们从分析模型如何沿着数据、设备、浏览器和区域的分类维度估计异质处理效应开始。 对于每个分类变量,我们绘制了实际和估计的平均处理效果。 作者提供的每个分类值的真实和估计处理效果 因果森林算法非常善于预测与分类变量相关的处理效果。至于因果树,这是预期的,因为算法具有非常离散的性质。然而,与因果树不同的是,预测更加微妙。 我们现在可以做一个更相关的测试:算法在时间等连续变量下的表现如何?首先,让我们再次隔离预测的处理效果,并忽略其他协变量。 def compute_time_effect(df, hte_model, avg_effect_notime): 我们现在可以复制之前的数字,但时间维度除外。我们绘制了一天中每个时间的平均真实和估计处理效果。 沿时间维度绘制的真实和估计的处理效果 我们现在可以充分理解因果树和森林之间的区别:虽然在因果树的情况下,估计基本上是一个非常粗略的阶跃函数,但我们现在可以看到因果树如何产生更平滑的估计。 我们现在已经探索了该模型,是时候使用它了! 假设我们正在考虑向访问我们在线商店的新客户提供4美元的折扣。 折扣对哪些客户有效?我们估计平均处理效果为1.9492美元。这意味着,平均而言折扣并不真正有利可图。然而,现在可以针对单个客户,我们只能向一部分新客户提供折扣。我们现在将探讨如何进行政策目标定位,为了更好地了解目标定位的质量,我们将使用因果树模型作为参考点。 我们使用相同的CauselForestML函数构建因果树,但将估计数和森林大小限制为1。 接下来,我们将数据集分成一个训练集和一个测试集。这一想法与交叉验证非常相似:我们使用训练集来训练模型——在我们的案例中是异质处理效应的估计器——并使用测试集来评估其质量。主要区别在于,我们没有观察到测试数据集中的真实结果。但是我们仍然可以使用训练测试分割来比较样本内预测和样本外预测。 我们将所有观察结果的80%放在训练集中,20%放在测试集中。 首先,让我们仅在训练样本上重新训练模型。 现在,我们可以确定目标策略,即决定我们向哪些客户提供折扣。答案似乎很简单:我们向所有预期处理效果大于成本(4美元)的客户提供折扣。 借助于一个可视化工具,它可以让我们了解处理对谁有效以及如何有效,这就是所谓的处理操作特征(TOC)曲线。这个名字可以看作是基于另一个更著名的接收器操作特性(ROC)曲线的修正,该曲线描绘了二元分类器的不同阈值的真阳性率与假阳性率。这两种曲线的想法类似:我们绘制不同比例受处理人群的平均处理效果。在一个极端情况下,当所有客户都被处理时,曲线的值等于平均处理效果;而在另一个极端情况下,当只有一个客户被处理时曲线的值则等于最大处理效果。 现在让我们计算曲线。 现在,我们可以绘制两个CATE估算器的处理操作特征(TOC)曲线。 处理操作特性曲线 正如预期的那样,两种估算器的TOC曲线都在下降,因为平均效应随着我们处理客户份额的增加而降低。换言之,我们在发布折扣时越有选择,每个客户的优惠券效果就越高。我还画了一条带有折扣成本的水平线,以便我们可以将TOC曲线下方和成本线上方的阴影区域解释为预期利润。 这两种算法预测的处理份额相似,约为20%,因果森林算法针对的客户略多一些。然而,他们预测的利润结果却大相径庭。因果树算法预测的边际较小且恒定,而因果林算法预测的是更大且更陡的边际。那么,哪一种算法更准确呢? 为了比较它们,我们可以在测试集中对它们进行评估。我们采用训练集上训练的模型,预测处理效果,并将其与测试集上训练模型的预测进行比较。注意,与机器学习标准测试程序不同,有一个实质性的区别:在我们的案例中,我们无法根据实际情况评估我们的预测,因为没有观察到处理效果。我们只能将两个预测相互比较。 因果树模型似乎比因果森林模型表现得更好一些,总净效应为8386美元——相对于4948美元。从图中,我们也可以了解差异的来源。因果森林算法往往限制性更强,处理的客户更少,没有误报的阳性,但也有很多误报的阴性。另一方面,因果树算法看起来更加“慷慨”,并将折扣分配给更多的新客户。这既转化为更多的真阳性,也转化为假阳性。总之,净效应似乎有利于因果树算法。 通常,我们讨论到这里就可以停止了,因为我们可以做的事情不多了。然而,在我们的案例情形中,我们还可以访问真正的数据生成过程。因此,接下来我们不妨检查一下这两种算法的真实精度。 首先,让我们根据处理效果的预测误差来比较它们。对于每个算法,我们计算处理效果的均方误差。 结果是,随机森林模型更好地预测了平均处理效果,均方误差为0.5555美元,而不是0.9035美元。 那么,这是否意味着更好的目标定位呢?我们现在可以复制上面所做的相同的柱状图,以了解这两种算法在策略目标方面的表现。 这两幅图非常相似,但结果却大相径庭。事实上,因果森林算法现在优于因果树算法,总效果为10395美元,而非8828美元。为什么会出现这种突然的差异呢? 为了更好地理解差异的来源,让我们根据实际情况绘制TOC。 处理操作特性曲线。 正如我们所看到的,TOC是倾斜度非常大的,存在一些平均处理效果非常高的客户。随机森林算法能够更好地识别它们,因此总体上更有效,尽管目标客户较少些。 Dans cet article, nous apprenons une fonction estimation très puissante des effets de traitement hétérogènesde l'algorithme— forêt causale. Les forêts causales sont construites sur les mêmes principes que les arbres causals, mais bénéficient d'une exploration plus approfondie de l'espace des paramètres et des algorithmes de bagging . De plus, nous comprenons également comment utiliser les estimations des effets hétérogènes des traitements pour mettre en œuvre une politique de positionnement. En identifiant les utilisateurs ayant la plus grande efficacité de traitement , nous sommes en mesure de garantir qu'une politique est rentable. Nous constatons également que les objectifs politiques diffèrent des objectifs d’estimation des effets hétérogènes du traitement, car les queues de la distribution peuvent avoir des corrélations plus fortes que la moyenne . 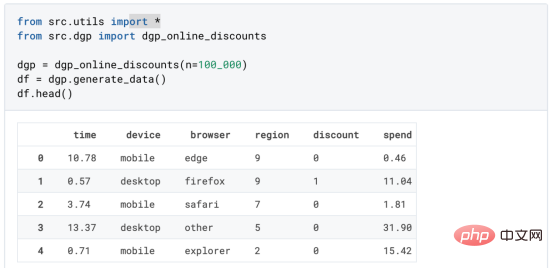
Forêt causale
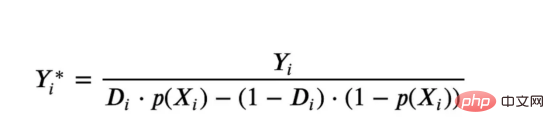
df_dummies = pd.get_dummies(df[dgp.X[1:]], drop_first=True)
df = pd.concat([df, df_dummies], axis=1)
X = ['time'] + list(df_dummies.columns)
Maintenant, nous pouvons utiliser l'algorithme de forêt aléatoire pour estimer les effets hétérogènes du traitement. Heureusement, nous n'avons pas besoin de faire tout cela manuellement, car fournit déjà une belle implémentation des arbres et forêts causales dans le package EconML de Microsoft . Nous utiliserons la fonction CausalForestML de . from econml.dml import CausalForestDML
np.random.seed(0)
forest_model = CausalForestDML(max_depth=3)
forest_model = forest_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
from econml.cate_interpreter import SingleTreeCateInterpreter
intrp = SingleTreeCateInterpreter(max_depth=2).interpret(forest_model, df[X])
intrp.plot(feature_names=X, fnotallow=12)

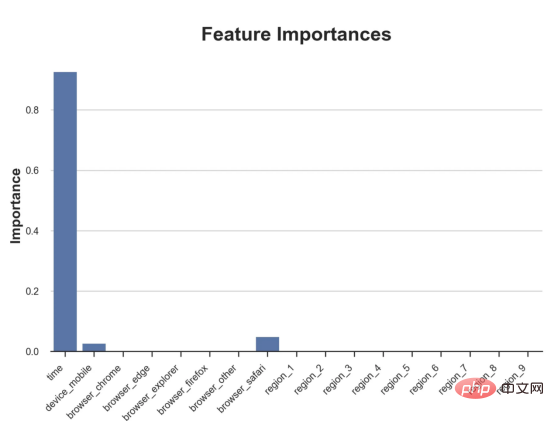
性能
def compute_discrete_effects(df, hte_model):
temp_df = df.copy()
temp_df.time = 0
temp_df = dgp.add_treatment_effect(temp_df)
temp_df = temp_df.rename(columns={'effect_on_spend': 'True'})
temp_df['Predicted'] = hte_model.effect(temp_df[X])
df_effects = pd.DataFrame()
for var in X[1:]:
for effect in ['True', 'Predicted']:
v = temp_df.loc[temp_df[var]==1, effect].mean() - temp_df[effect][temp_df[var]==0].mean()
effect_var = {'Variable': [var], 'Effect': [effect], 'Value': [v]}
df_effects = pd.concat([df_effects, pd.DataFrame(effect_var)]).reset_index(drop=True)
return df_effects, temp_df['Predicted'].mean()
df_effects, avg_effect_notime = compute_discrete_effects(df, forest_model)fig, ax = plt.subplots()
sns.barplot(data=df_effects, x="Variable", y="Value", hue="Effect", ax=ax).set(
xlabel='', ylabel='', title='Heterogeneous Treatment Effects')
ax.set_xticklabels(ax.get_xticklabels(), rotatinotallow=45, ha="right");
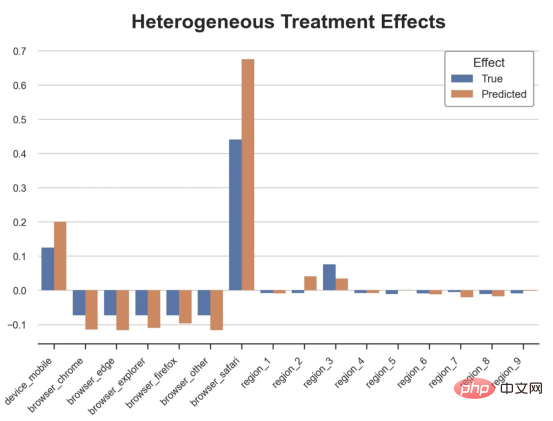
df_time = df.copy()
df_time[[X[1:]] + ['device', 'browser', 'region']] = 0
df_time = dgp.add_treatment_effect(df_time)
df_time['predicted'] = hte_model.effect(df_time[X]) + avg_effect_notime
return df_time
df_time = compute_time_effect(df, forest_model, avg_effect_notime)
sns.scatterplot(x='time', y='effect_on_spend', data=df_time, label='True')
sns.scatterplot(x='time', y='predicted', data=df_time, label='Predicted').set(
ylabel='', title='Heterogeneous Treatment Effects')
plt.legend(title='Effect');
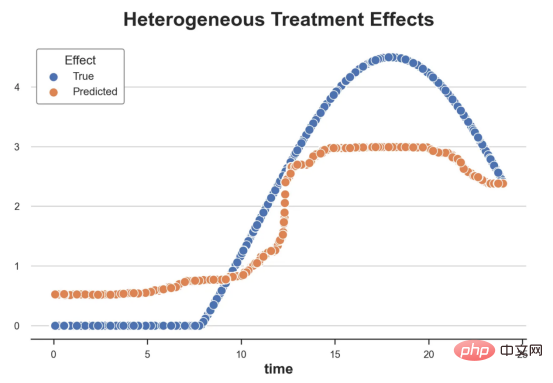
策略定位
cost = 4
from econml.dml import CausalForestDML
np.random.seed(0)
tree_model = CausalForestDML(n_estimators=1, subforest_size=1, inference=False, max_depth=3)
tree_model = tree_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
df_train, df_test = df.iloc[:80_000, :], df.iloc[20_000:,]
np.random.seed(0)
tree_model = tree_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
forest_model = forest_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
def compute_toc(df, hte_model, cost, truth=False):
df_toc = pd.DataFrame()
for q in np.linspace(0, 1, 101):
if truth:
df = dgp.add_treatment_effect(df_test)
effect = df['effect_on_spend']
else:
effect = hte_model.effect(df[X])
ate = np.mean(effect[effect >= np.quantile(effect, 1-q)])
temp = pd.DataFrame({'q': [q], 'ate': [ate]})
df_toc = pd.concat([df_toc, temp]).reset_index(drop=True)
return df_toc
df_toc_tree = compute_toc(df_train, tree_model, cost)
df_toc_forest = compute_toc(df_train, forest_model, cost)def plot_toc(df_toc, cost, ax, color, title):
ax.axhline(y=cost, lw=2, c='k')
ax.fill_between(x=df_toc.q, y1=cost, y2=df_toc.ate, where=(df_toc.ate > cost), color=color, alpha=0.3)
if any(df_toc.ate > cost):
q = df_toc_tree.loc[df_toc.ate > cost, 'q'].values[-1]
else:
q = 0
ax.axvline(x=q, ymin=0, ymax=0.36, lw=2, c='k', ls='--')
sns.lineplot(data=df_toc, x='q', y='ate', ax=ax, color=color).set(
title=title, ylabel='ATT', xlabel='Share of treated', ylim=[1.5, 8.5])
ax.text(0.7, cost+0.1, f'Discount cost: {cost:.0f}$', fnotallow=12)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
plot_toc(df_toc_tree, cost, ax1, 'C0', 'TOC - Causal Tree')
plot_toc(df_toc_forest, cost, ax2, 'C1', 'TOC - Causal Forest')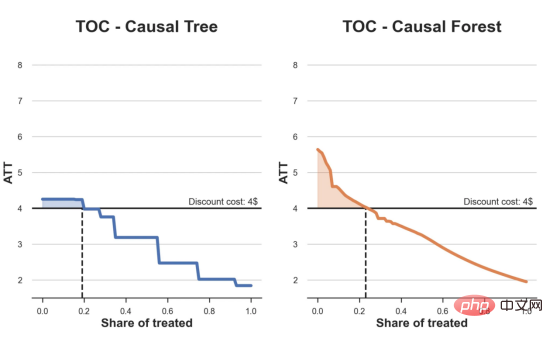
def compute_effect_test(df_test, hte_model, cost, ax, title, truth=False):
df_test['Treated'] = hte_model.effect(df_test[X]) > cost
if truth:
df_test = dgp.add_treatment_effect(df_test)
df_test['Effect'] = df_test['effect_on_spend']
else:
np.random.seed(0)
hte_model_test = copy.deepcopy(hte_model).fit(Y=df_test[dgp.Y], X=df_test[X], T=df_test[dgp.D])
df_test['Effect'] = hte_model_test.effect(df_test[X])
df_test['Cost Effective'] = df_test['Effect'] > cost
tot_effect = ((df_test['Effect'] - cost) * df_test['Treated']).sum()
sns.barplot(data=df_test, x='Cost Effective', y='Treated', errorbar=None, width=0.5, ax=ax, palette=['C3', 'C2']).set(
title=title + 'n', ylim=[0,1])
ax.text(0.5, 1.08, f'Total effect: {tot_effect:.2f}', fnotallow=14, ha='center')
return
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree')
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest')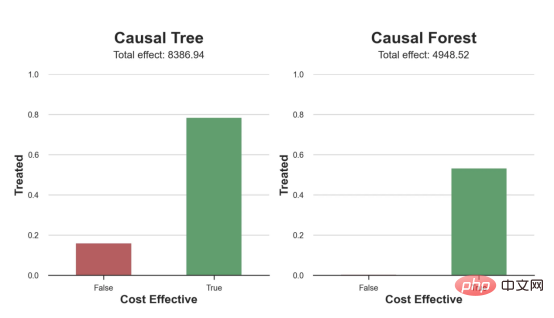
from sklearn.metrics import mean_squared_error as mse
def compute_mse_test(df_test, hte_model):
df_test = dgp.add_treatment_effect(df_test)
print(f"MSE = {mse(df_test['effect_on_spend'], hte_model.effect(df_test[X])):.4f}")
compute_mse_test(df_test, tree_model)
compute_mse_test(df_test, forest_model)fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree', True)
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest', True)
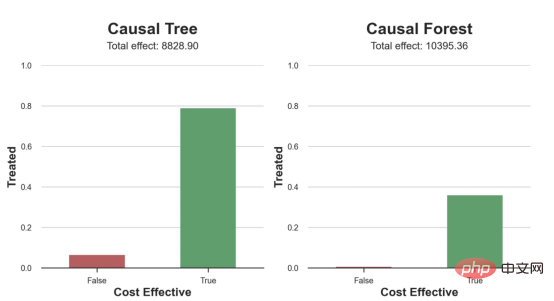
df_toc = compute_toc(df_test, tree_model, cost, True)
fix, ax = plt.subplots(1, 1, figsize=(7, 5))
plot_toc(df_toc, cost, ax, 'C2', 'TOC - Ground Truth')
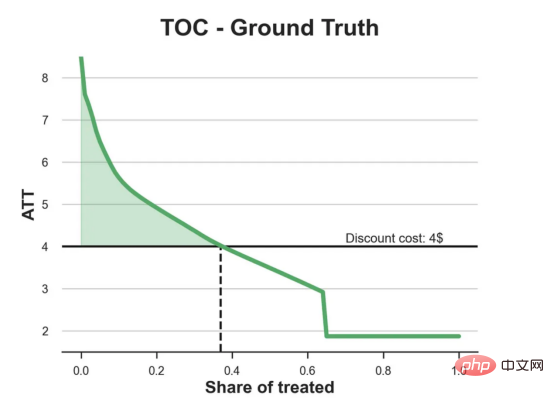
Conclusion
Références
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

